Bar-Meir G. Fundamentals of Compressible Fluid

Подождите немного. Документ загружается.

13.1. GENERAL MODEL 251

The governing equation (12.10) that was developed in the previous Chapter

(12) obtained the form as

max

Mf(M)

k+1

= 0 (13.3)

where

t = t/t

max

. Notice that in this case that there are two diﬀerent character-

istic times: the “characteristic” time, t

and the “maximum” time, t

max

. The ﬁrst

characteristic time, t

is associated with the ratio of the volume and the tube charac-

teristics (see equation (12.5)). The second characteristic time, t

max

is associated with

the imposed time on the system (in this case the elapsed time of the piston stroke).

Equation (13.3) is an nonlinear ﬁrst order diﬀerential equation and can be

rearranged as follows

1 −

max

Mf[M]

k−1

1 −

;

P (0) = 1. (13.4)

Equation (13.4) is can be solved only when the ﬂow is chocked In which case f[m]

isn’t function of the time.

The solution of equation (13.4)) can be obtained by transforming and by in-

troducing a new variable ξ =

k−1

and therefore

P = [ξ]

k−1

. The reduced Pressure

derivative, d

P =

k−1

[ξ]

(

k−1

)

−1

dξ Utilizing this deﬁnition and there implication reduce

equation (13.4)

2 [ξ]

(

k−1

)

−1

dξ

(k − 1) (1 − Bξ) [ξ]

k−1

1 −

(13.5)

where B =

max

Mf[M] And equation (13.5) can be further simpliﬁed as

2dξ

(k − 1) (1 − Bξ) ξ

1 −

(13.6)

Equation (13.6) can be integrated to obtain

(k − 1)B

1 −Bξ

= −ln

t (13.7)

or in a diﬀerent form

1 −Bξ

(1−k)B

t (13.8)

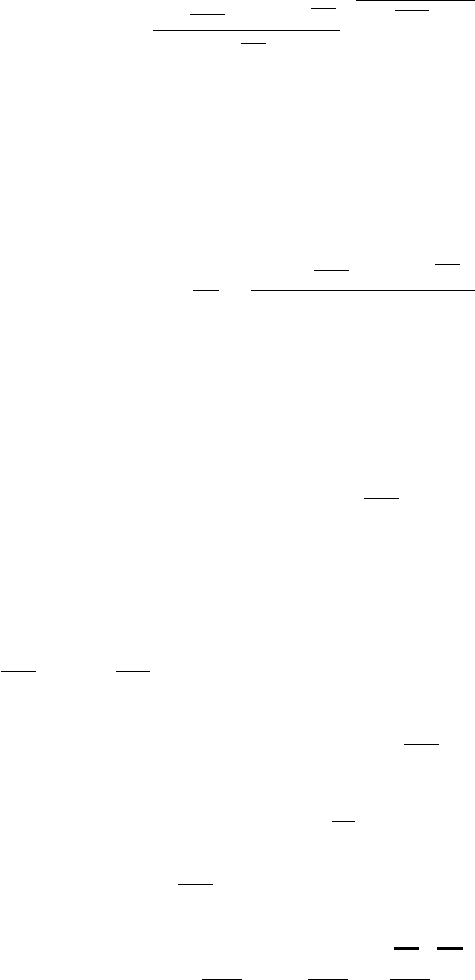
252 CHAPTER 13. Evacuating under External Volume Control

Now substituting to the “preferred” variable

1 −

max

Mf[M]

k−1

(1−k)

max

Mf [M]

t (13.9)

The analytical solution is applicable only in the case which the ﬂow is choked thor-

ough all the process. The solution is applicable to indirect connection. This happen

when vacuum is applied outside the tube (a technique used in die casting and injection

molding to improve quality by reducing porosity.). In case when the ﬂow chokeless

a numerical integration needed to be performed. In the literature, to create a direct

function equation (13.4) is transformed into

1 −

max

Mf[M]

k−1

1 −

(13.10)

with the initial condition of

P (0) = 1 (13.11)

The analytical solution also can be approximated by a simpler equation as

P = [1 − t]

max

(13.12)

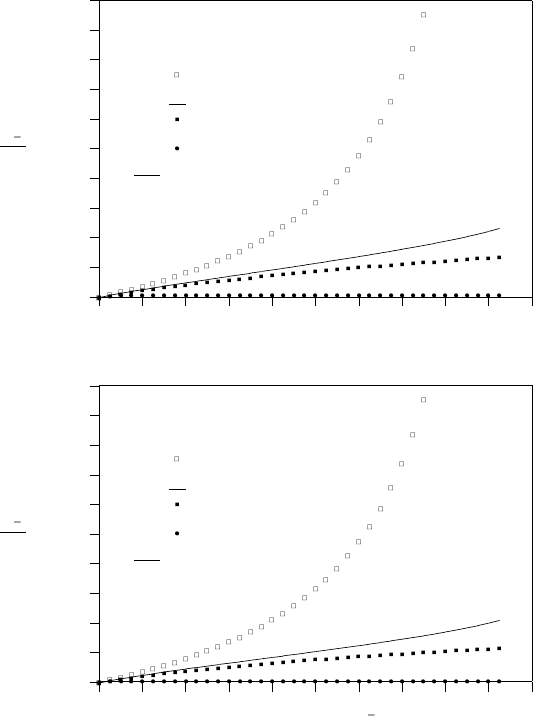
The results for numerical evaluation in the case when cylinder is initially at an at-

mospheric pressure and outside tube is also at atmospheric pressure are presented in

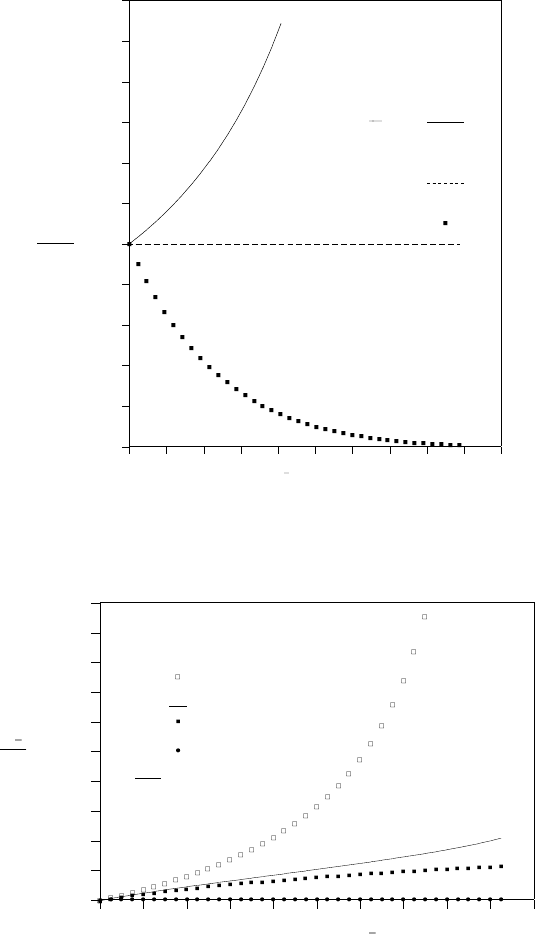
Figure (13.2). In this case only some part of the ﬂow is choked (the later part). The

results of a choked case are presented in Figure (13.3) in which outside tube condition

is in vacuum. These Figures (13.2) and 13.3 demonstrate the importance of the ratio

max

. When

max

> 1 the pressure increases signiﬁcantly and verse versa. Thus,

the question remains how the time ratio can be transfered to parameters that can the

engineer can design in the system.

Denoting the area that creates the ratio

max

= 1 as the critical area, A

provides the needed tool. Thus the exit area, A can be expressed as

A =

(13.13)

The actual times ratio

max

can be expressed as

max

z }| {

max

(13.14)

13.1. GENERAL MODEL 253

According to equation (12.5) t

is inversely proportional to area, t

∝ 1/A. Thus,

equation (13.14) the t

max

is canceled and reduced into

max

(13.15)

Parameters inﬂuencing the process are the area ratio,

, and the friction pa-

rameter,

4fL

. From other detailed calculations the author’s thesis (later to be published

at this site: www.potto.org). it was found that the inﬂuence of the parameter

4fL

the pressure development in the cylinder is quite small. The inﬂuence is small on the

residual air mass in the cylinder but larger on the Mach number, M

exit

. The eﬀects of

the area ratio,

, are studied here since it is the dominant parameter.

It is important to point out the signiﬁcance of the

max

. This parameter

represents the ratio between the ﬁlling time and the evacuating time, the time which

would be required to evacuate the cylinder for constant mass ﬂow rate at the maximum

Mach number when the gas temperature and pressure remain in their initial values.

This parameter also represents the dimensionless area,

, according to the following

equation

Figure (13.4) describes the pressure as a function of the dimensionless time for

various values of

. The line that represents

= 1 is almost straight. For large

values of

the pressure increases the volume ﬂow rate of the air until a quasi steady

state is reached. This quasi steady state is achieved when the volumetric air ﬂow rate

out is equal to the volume pushed by the piston. The pressure and the mass ﬂow rate

are maintained constant after this state is reached. The pressure in this quasi steady

state is a function of

. For small values of

there is no steady state stage. When

is greater than one the pressure is concave upward and when

is less than one

the pressure is concave downward as shown in Figures (13.4), which was obtained by

an integration of equation (13.9).

13.1.2 Examples

Example 13.1:

Calculate the minimum required vent area for die casting process when the die volume

is 0.001[m

] and

4fL

= 20. The required solidiﬁcation time, t

max

= 0.03[sec].

Solution

End solution

13.1.3 Direct Connection

In the above analysis is applicable to indirect connection. It should be noted that critical

area, A

, is not function of the time. The direct connection posts more mathematical

diﬃculty because the critical area is not constant and time dependent.

254 CHAPTER 13. Evacuating under External Volume Control

To continue

13.2 Summary

The analysis indicates there is a critical vent area below which the ventilation is poor

and above which the resistance to air ﬂow is minimal. This critical area depends on the

geometry and the ﬁlling time. The critical area also provides a mean to “combine” the

actual vent area with the vent resistance for numerical simulations of the cavity ﬁlling,

taking into account the compressibility of the gas ﬂow.

13.2. SUMMARY 255

∗

∇

Dimensionless

Area,

A/A

0.0

0.2

0.5

1.0

1.2

2.0

5.0

4fL

1.0

1.4

1.8

2.2

2.6

3.0

3.4

3.8

4.2

4.6

5.0

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

P(t)

(0)

100.0

∗

∇

∗

∇

Dimensionless

Area, A/A

0.0

0.2

0.5

1.0

1.2

2.0

5.0

4fL

Dimensionless Time, t,

or, Cylinder Volume Fraction

1.0

1.4

1.8

2.2

2.6

3.0

3.4

3.8

4.2

4.6

5.0

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

)

P(0)

5.0

∗

∇

Figure b

Figure a

Fig. -13.2. The pressure ratio as a function of the dimensionless time for chokeless condition

256 CHAPTER 13. Evacuating under External Volume Control

P(t)

P(0)

DIMENSIONLESS TIME, t, or, CYLINDER VOLUME FRACTION

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

2.2

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

..........

∗

0.0

0.1

0.5

1.0

1.5

4.0

∗

Fig. -13.3. The pressure ratio as a function of the dimensionless time for choked condition

∗

∇

Dimensionless

Area, A/A

0.0

0.2

0.5

1.0

1.2

2.0

5.0

4fL

Dimensionless

Time,

or, Cylinder Volume Fraction

1.0

1.4

1.8

2.2

2.6

3.0

3.4

3.8

4.2

4.6

5.0

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

)

(0)

5.0

∗

∇

Fig. -13.4. The pressure ratio as a function of the dimensionless time

CHAPTER 14

Oblique Shock

14.1 Preface to Oblique Shock

= 0

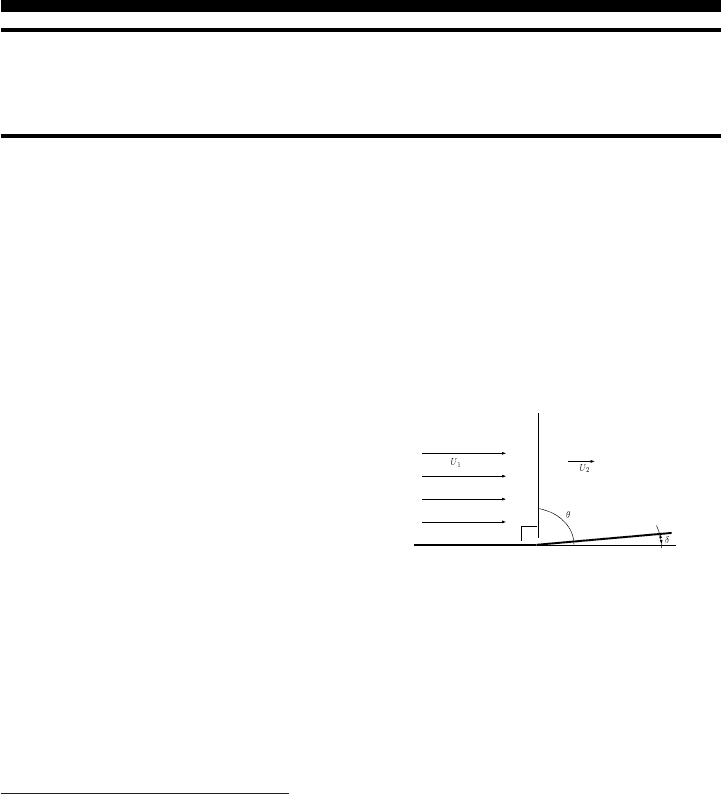
Fig. -14.1. A view of a straight normal shock

as a limited case for oblique shock.

In Chapter (6), discussion on a normal

shock was presented. A normal shock is

a special type of shock wave. The other

type of shock wave is the oblique shock.

In the literature oblique shock, nor-

mal shock, and Prandtl–Meyer function

are presented as three separate and dif-

ferent issues. However, one can view all

these cases as three diﬀerent regions of a

ﬂow over a plate with a deﬂection section.

Clearly, variation of the deﬂection angle from a zero (δ = 0) to a positive value results

in oblique shock. Further changing the deﬂection angle to a negative value results in

expansion waves. The common representation is done by not showing the boundaries

of these models. However, this section attempts to show the boundaries and the limits

or connections of these models

In this chapter, even the whole book, a very limited discussion about reﬂection shocks and collisions

of weak shock, Von Neumann paradox, triple shock intersection, etc are presented. The author believes

that these issues are not relevant to most engineering students and practices. Furthermore, these issues

should not be introduced in introductory textbook of compressible ﬂow. Those who would like to obtain

more information, should refer to J.B. Keller, “Rays, waves and asymptotics,” Bull. Am. Math. Soc.

84, 727 (1978), and E.G. Tabak and R.R. Rosales, “Focusing of weak shock waves and the Von Neuman

paradox of oblique shock reﬂection,” Phys. Fluids 6, 1874 (1994).

257

258 CHAPTER 14. OBLIQUE SHOCK

14.2 Introduction

14.2.1 Introduction to Oblique Shock

A normal shock o ccurs when there is a disturbance downstream which imposes a bound-

ary condition on the ﬂow in which the ﬂuid/gas can react only by a sharp change in the

ﬂow direction. As it may be recalled, normal shock occurs when a wall is straight/ﬂat

(δ = 0) as shown in Figure (14.1) which occurs when somewhere downstream a distur-

bance

appears. When the deﬂection angle is increased, the gas ﬂow must match the

boundary conditions. This matching can occur only when there is a discontinuity in the

ﬂow ﬁeld. Thus, the direction of the ﬂow is changed by a shock wave with an angle

to the ﬂow. This shock is commonly referred to as the oblique shock. Alternatively, as

discussed in Chapter (1)

the ﬂow behaves as it does in a hyperbolic ﬁeld. In such a

case, the ﬂow ﬁeld is governed by a hyperbolic equation which deals with the case when

information (like boundary conditions) reaches from downstream only if they are within

the range of inﬂuence. For information such as the disturbance (b oundary condition) to

reach deep into the ﬂow from the side requires time. During this time, the ﬂow moves

downstream and creates an angle.

14.2.2 Introduction to Prandtl–Meyer Function

◦

No Shock

zone

Oblique

Shock

max

(k)

Prandtl

Meyer

Function

∞

(k)

Fig. -14.2. The regions where oblique shock or

Prandtl–Meyer function exist. Notice that b oth

have a maximum point and a “no solution” zone,

which is around zero. However, Prandtl-Meyer func-

tion approaches closer to a zero deﬂection angle.

Decreasing the deﬂection angle results

in the same eﬀects as before. The

boundary conditions must match the

geometry. Yet, for a negative deﬂec-

tion angle (in this section’s notation),

the ﬂow must be continuous. The

analysis shows that the ﬂow velocity

must increase to achieve this require-

ment. This velocity increase is referred

to as the expansion wave. As it will be

shown in the next chapter, as opposed

to oblique shock analysis, the increase in the upstream Mach number determines the

downstream Mach number and the “negative” deﬂection angle.

It has to be pointed out that both the oblique shock and the Prandtl–Meyer

function have a maximum point for M

→ ∞. However, the maximum point for the

Prandtl–Meyer function is much larger than the oblique shock by a factor of more than

2. What accounts for the larger maximum point is the eﬀective turning (less entropy

production) which will be explained in the next chapter (see Figure (14.2)).

Zero velocity, pressure boundary conditions, and diﬀerent inclination angle, are examples of forces

that create shock. The zero velocity can be found in a jet ﬂowing into a still medium of gas.

This section is under construction and does not appear in the book yet.

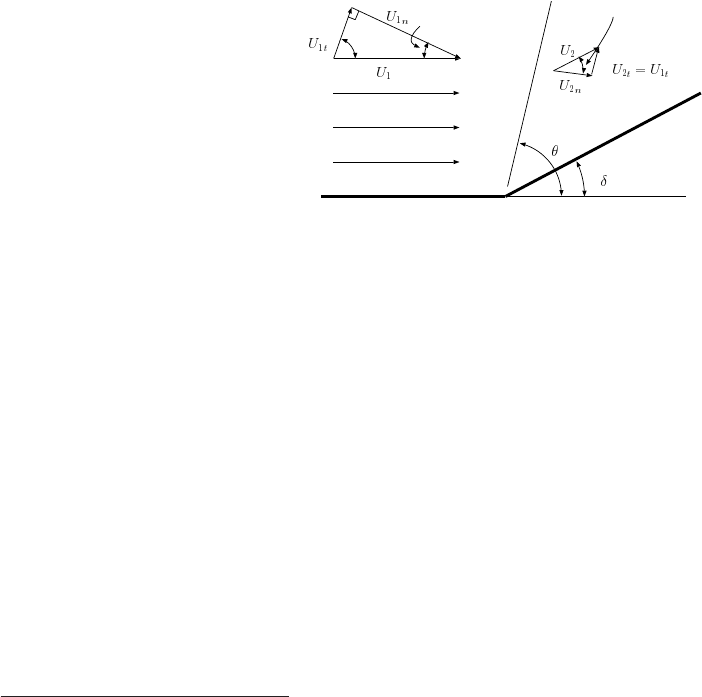
14.3. OBLIQUE SHOCK 259

14.2.3 Introduction to Zero Inclination

What happens when the inclination angle is zero? Which model is correct to use? Can

these two conﬂicting models, the oblique shock and the Prandtl–Meyer function, co-

exist? Or perhaps a diﬀerent model better describes the physics. In some books and

in the famous NACA report 1135 it was assumed that Mach wave and oblique shock

co–occur in the same zone. Previously (see Chapter 6), it was assumed that normal

shock occurs at the same time. In this chapter, the stability issue will be examined in

greater detail.

14.3 Oblique Shock

Comparsion Line

π/2 − θ

θ − δ

Fig. -14.3. A typical oblique shock schematic

The shock occurs in reality in

situations where the shock has

three–dimensional eﬀects. The

three–dimensional eﬀects of the

shock make it appear as a

curved plane. However, for a

chosen arbitrary accuracy it re-

quires a speciﬁc small area, a

one–dimensional shock can be

considered. In such a case, the

change of the orientation makes

the shock considerations two–

dimensional. Alternately, using an inﬁnite (or a two–dimensional) object produces a

two–dimensional shock. The two–dimensional eﬀects o ccur when the ﬂow is aﬀected

from the “side,” i.e., a change in the ﬂow direction

To match the boundary conditions, the ﬂow turns after the shock to be parallel

to the inclination angle. Figure (14.3) exhibits the schematic of the oblique shock. The

deﬂection angle, δ, is the direction of the ﬂow after the shock (parallel to the wall).

The normal shock analysis dictates that after the shock, the ﬂow is always subsonic.

The total ﬂow after the oblique sho ck can also be supersonic, which depends on the

boundary layer.

Only the oblique shock’s normal component undergoes the “shock.” The tangent

component does not change because it does not “move” across the shock line. Hence,

the mass balance reads

= ρ

(14.1)

The momentum equation reads

+ ρ

= P

+ ρ

(14.2)

The author begs for forgiveness from those who view this description as oﬀensive (There was an

unpleasant email to the author accusing him of revolt against the holy of the holies.). If you do not

like this description, please just ignore it. You can use the traditional explanation, you do not need the

author’s permission.

260 CHAPTER 14. OBLIQUE SHOCK

The momentum equation in the tangential direction yields

= U

(14.3)

The energy balance reads

= C

(14.4)

Equations (14.1), (14.2), and (14.4) are the same as the equations for normal shock

with the exception that the total velocity is replaced by the perpendicular components.

Yet the new relationship between the upstream Mach number, the deﬂection angle,

δ, and the Mach angle, θ has to be solved. From the geometry it can be observed that

tan θ =

(14.5)

and

tan(θ − δ) =

(14.6)

Unlike in the normal shock, here there are three possible pairs

of solutions to

these equations. The ﬁrst is referred to as the weak shock; the second is the strong

shock; and the third is an impossible solution (thermodynamically)

. Experiments and

experience have shown that the common solution is the weak shock, in which the shock

turns to a lesser extent

tan θ

tan(θ − δ)

(14.7)

The above velocity–geometry equations can also be expressed in term of Mach number,

sin θ =

(14.8)

sin(θ − δ) =

(14.9)

cos θ =

(14.10)

This issue is due to R. Menikoﬀ, who raised the solution completeness issue.

The solution requires solving the entropy conservation equation. The author is not aware of

“simple” proof and a call to ﬁnd a simple proof is needed.

Actually this term is used from historical reasons. The lesser extent angle is the unstable angle

and the weak angle is the middle solution. But because the literature referred to only two roots, the

term lesser extent is used.