Bar-Meir G. Fundamentals of Compressible Fluid

Подождите немного. Документ загружается.

5.3. ISENTROPIC TABLES 81

3% (for k = 1.4). As can be observed from Figure (5.7(b)). The Mach number for

the isentropic is larger for the supersonic branch but the velocity is lower.

0.5

1.5

Distance (normalized distance two scales)

0.2

0.4

0.6

0.8

P / P

0 isentropic

T / T

0 isentropic

P / P

0 isothermal

T/T

0 isothermal

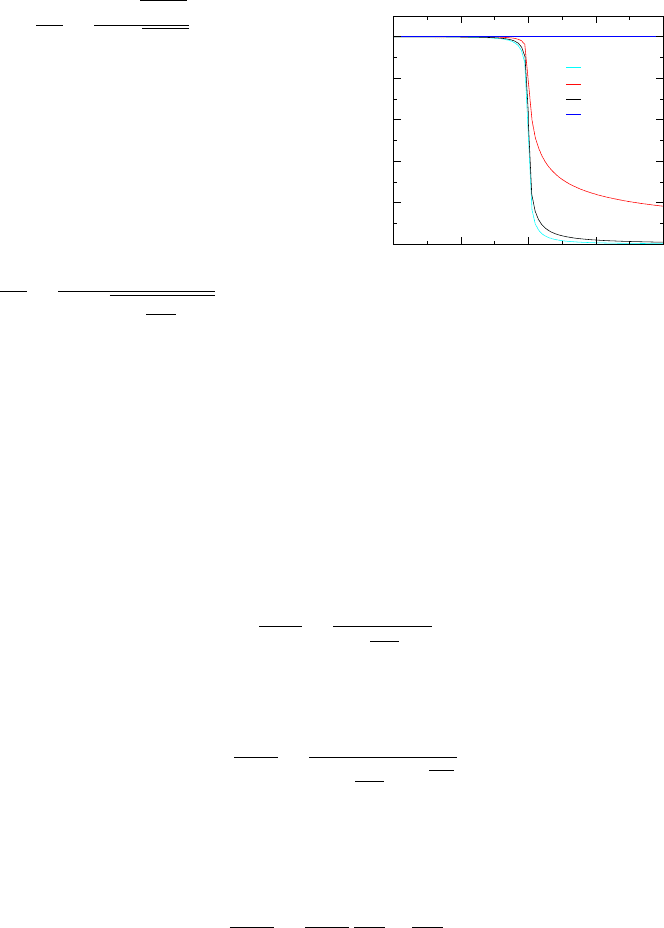
Comparison between the two models

k = 1 4

Fri Apr 8 15:11:44 2005

Fig. -5.8. Comparison of the pressure and tempera-

ture drop as a function of the normalized length (two

scales)

The ratio of the velocities can be ex-

pressed as

√

kRT

√

kRT

(5.99)

It can be noticed that temperature

in the isothermal model is constant

while temperature in the adiabatic

model can be expressed as a function

of the stagnation temperature. The

initial stagnation temperatures are al-

most the same and can be canceled

out to obtain

∼

1 +

k−1

(5.100)

By utilizing equation (5.100) the ve-

locity ratio was obtained and is plot-

ted in Figure (5.7(b)).

Thus, using the isentropic model results in under prediction of the actual results

for the velocity in the supersonic branch. While, the isentropic for the subsonic branch

will be over prediction. The prediction of the Mach number are similarly shown in Figure

(5.7(b)).

Two other ratios need to be examined: temperature and pressure. The initial

stagnation temperature is denoted as T

int

. The temperature ratio of T /T

int

can be

obtained via the isentropic model as

int

1 +

k−1

(5.101)

While the temperature ratio of the isothermal model is constant and equal to one (1).

The pressure ratio for the isentropic model is

int

1 +

k−1

(5.102)

and for the isothermal process the stagnation pressure varies and has to be taken into

account as the following:

int

∗

int

∗

isentropic

z}|{

(5.103)

82 CHAPTER 5. ISENTROPIC FLOW

where z is an arbitrary point on the nozzle. Using equations (5.88) and the isentropic

relationship, the sought ratio is provided.

Figure (5.8) shows that the range between the predicted temperatures of the two

models is very large, while the range between the predicted pressure by the two models

is relatively small. The meaning of this analysis is that transferred heat aﬀects the

temperature to a larger degree but the eﬀect on the pressure is much less signiﬁcant.

To demonstrate the relativity of the approach advocated in this book consider the

following example.

Example 5.7:

Consider a diverging–converging nozzle made out of wood (low conductive material)

with exit area equal entrance area. The throat area ratio to entrance area is 1:4 re-

spectively. The stagnation pressure is 5[Bar] and the stagnation temperature is 27

◦

Assume that the back pressure is low enough to have supersonic ﬂow without shock

and k = 1.4. Calculate the velocity at the exit using the adiabatic model. If the nozzle

was made from copper (a go od heat conductor) a larger heat transfer occurs, should

the velocity increase or decrease? What is the maximum possible increase?

Solution

The ﬁrst part of the question deals with the adiabatic model i.e. the conservation of the

stagnation properties. Thus, with known area ratio and known stagnation Potto–GDC

provides the following table:

A×P

∗

×P

0.14655 0.99572 0.98934 4.0000 0.98511 3.9405

2.9402 0.36644 0.08129 4.0000 0.02979 0.11915

With the known Mach number and temperature at the exit, the velocity can be cal-

culated. The exit temperature is 0.36644 × 300 = 109.9K. The exit velocity, then,

U = M

√

kRT = 2.9402

√

1.4 ×287 × 109.9 ∼ 617.93[m/sec]

Even for the isothermal model, the initial stagnation temperature is given as

300K. Using the area ratio in Figure (5.6) or using the Potto–GDC obtains the following

table

A×P

∗

×P

1.9910 1.4940 0.51183 4.0000 0.12556 0.50225

The exit Mach number is known and the initial temperature to the throat temperature

ratio can be calculated as the following:

ini

∗

1 +

k−1

1 +

k−1

= 0.777777778

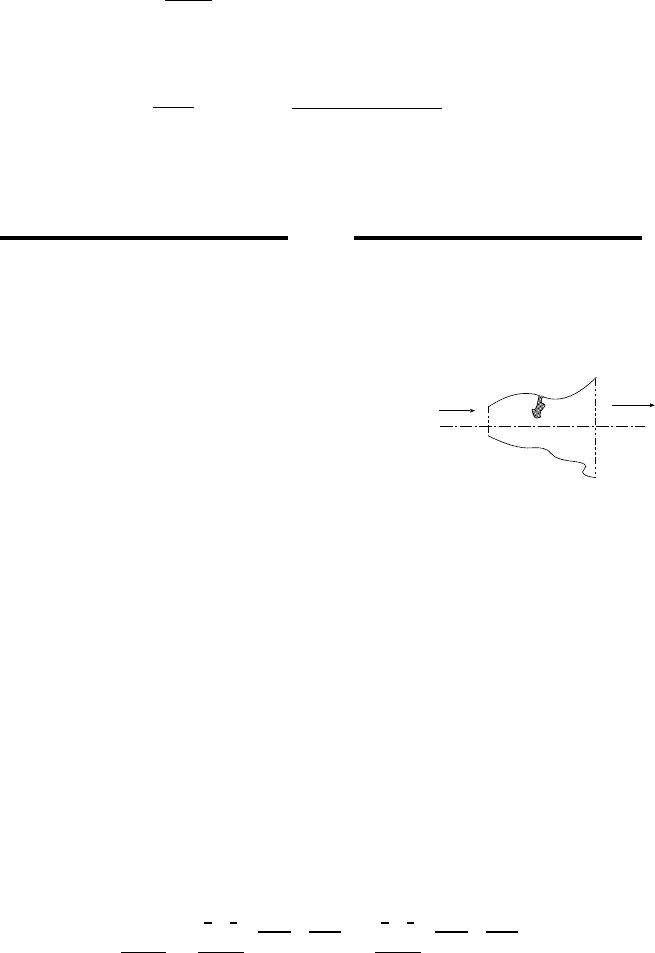
5.4. THE IMPULSE FUNCTION 83

Thus the stagnation temperature at the exit is

ini

exit

= 1.4940/0.777777778 = 1.921

The exit stagnation temperature is 1.92 × 300 = 576.2K. The exit velocity can be

determined by utilizing the following equation

exit

= M

√

kRT = 1.9910

√

1.4 ×287 × 300.0 = 691.253[m/sec]

As was discussed before, the velocity in the copper nozzle will be larger than

the velocity in the wood nozzle. However, the maximum velocity cannot exceed the

691.253[m/sec]

End solution

5.4 The Impulse Function

5.4.1 Impulse in Isentropic Adiabatic Nozzle

x-direction

Fig. -5.9. Schematic to explain the

signiﬁcances of the Impulse function.

One of the functions that is used in calculating the

forces is the Impulse function. The Impulse func-

tion is denoted here as F , but in the literature some

denote this function as I. To explain the motiva-

tion for using this deﬁnition consider the calculation

of the net forces that acting on section shown in

Figure (5.9). To calculate the net forces acting in

the x–direction the momentum equation has to be

applied

net

= ˙m(U

− U

) + P

− P

(5.104)

The net force is denoted here as F

net

. The mass conservation also can be applied to

our control volume

˙m = ρ

= ρ

(5.105)

Combining equation (5.104) with equation (5.105) and by utilizing the identity in

equation (5.42) results in

net

= kP

− kP

+ P

− P

(5.106)

Rearranging equation (5.106) and dividing it by P

∗

results in

net

∗

f(M

)

z}|{

∗

f(M

)

z }| {

1 + kM

−

f(M

)

z}|{

∗

f(M

)

z }| {

1 + kM

(5.107)

84 CHAPTER 5. ISENTROPIC FLOW

Examining equation (5.107) shows that the right hand side is only a function

of Mach number and speciﬁc heat ratio, k. Hence, if the right hand side is only a

function of the Mach number and k than the left hand side must be function of only

the same parameters, M and k. Deﬁning a function that depends only on the Mach

number creates the convenience for calculating the net forces acting on any device.

Thus, deﬁning the Impulse function as

F = P A

1 + kM

(5.108)

In the Impulse function when F (M = 1) is denoted as F

∗

= P

∗

(1 + k) (5.109)

The ratio of the Impulse function is deﬁned as

∗

1 + kM

(1 + k)

∗

|{z}

(

k+1

)

k−1

see function (5.107)

z }| {

∗

1 + kM

(1 + k)

(5.110)

This ratio is diﬀerent only in a coeﬃcient from the ratio deﬁned in equation (5.107)

which makes the ratio a function of k and the Mach number. Hence, the net force is

net

= P

∗

(1 + k)

k + 1

k−1

∗

−

∗

(5.111)

To demonstrate the usefulness of the this function consider a simple situation of

the ﬂow through a converging nozzle

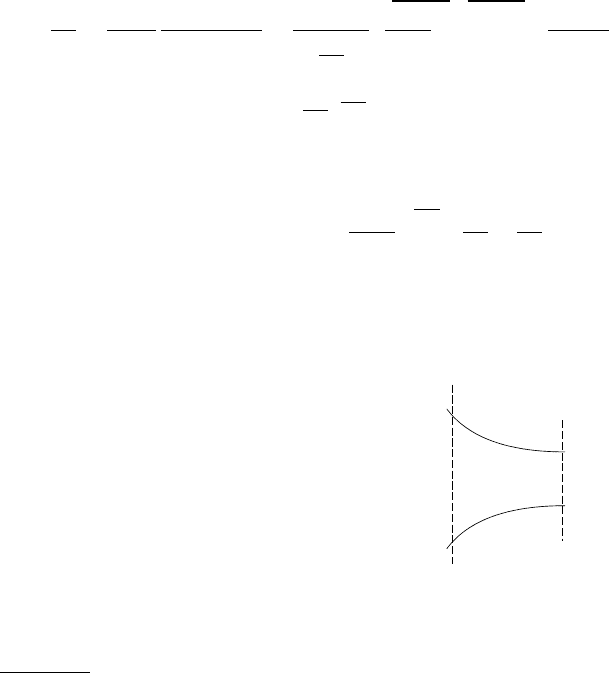
Example 5.8:

˙m = 1[kg/sec]

= 0.009m

= 400K

= 0.003m

= 50[Bar]

Fig. -5.10. Schematic of a ﬂow of a compressible sub-

stance (gas) through a converging nozzle for example

(5.8)

Consider a ﬂow of gas into a con-

verging nozzle with a mass ﬂow

rate of 1[kg/sec] and the en-

trance area is 0.009[m

] and the

exit area is 0.003[m

]. The stag-

nation temperature is 400K and

the pressure at point 2 was mea-

sured as 5[Bar ] Calculate the net

force acting on the nozzle and

pressure at point 1.

Solution

The solution is obtained by getting the data for the Mach number. To obtained the

5.4. THE IMPULSE FUNCTION 85

Mach number, the ratio of P

∗

is needed to be calculated. To obtain this ratio

the denominator is needed to be obtained. Utilizing Fliegner’s equation (5.51), provides

the following

∗

˙m

√

0.058

1.0 ×

√

400 ×287

0.058

∼ 70061.76[N]

and

∗

500000 ×0.003

70061.76

∼ 2.1

A×P

∗

×P

∗

0.27353 0.98526 0.96355 2.2121 0.94934 2.1000 0.96666

With the area ratio of

= 2.2121 the area ratio of at point 1 can be calculated.

= 2.2121 ×

0.009

0.003

= 5.2227

And utilizing again Potto-GDC provides

A×P

∗

×P

∗

0.11164 0.99751 0.99380 5.2227 0.99132 5.1774 2.1949

The pressure at point 1 is

= P

= 5.0times0.94934/0.99380 ∼ 4.776[Bar]

The net force is obtained by utilizing equation (5.111)

net

= P

∗

(1 + k)

k + 1

k−1

∗

−

∗

= 500000 ×

2.1

× 2.4 × 1.2

3.5

× (2.1949 − 0.96666) ∼ 614[kN]

End solution

5.4.2 The Impulse Function in Isothermal Nozzle

Previously Impulse function was developed in the isentropic adiabatic ﬂow. The same

is done here for the isothermal nozzle ﬂow model. As previously, the deﬁnition of the

86 CHAPTER 5. ISENTROPIC FLOW

Impulse function is reused. The ratio of the impulse function for two points on the

nozzle is

+ ρ

(5.112)

Utilizing the ideal gas model for density and some rearrangement results in

1 +

(5.113)

Since U

/RT = kM

and the ratio of equation (5.86) transformed equation into

(5.113)

1 + kM

(5.114)

At the star condition (M = 1) (not the minimum point) results in

∗

1 + kM

1 + k

(5.115)

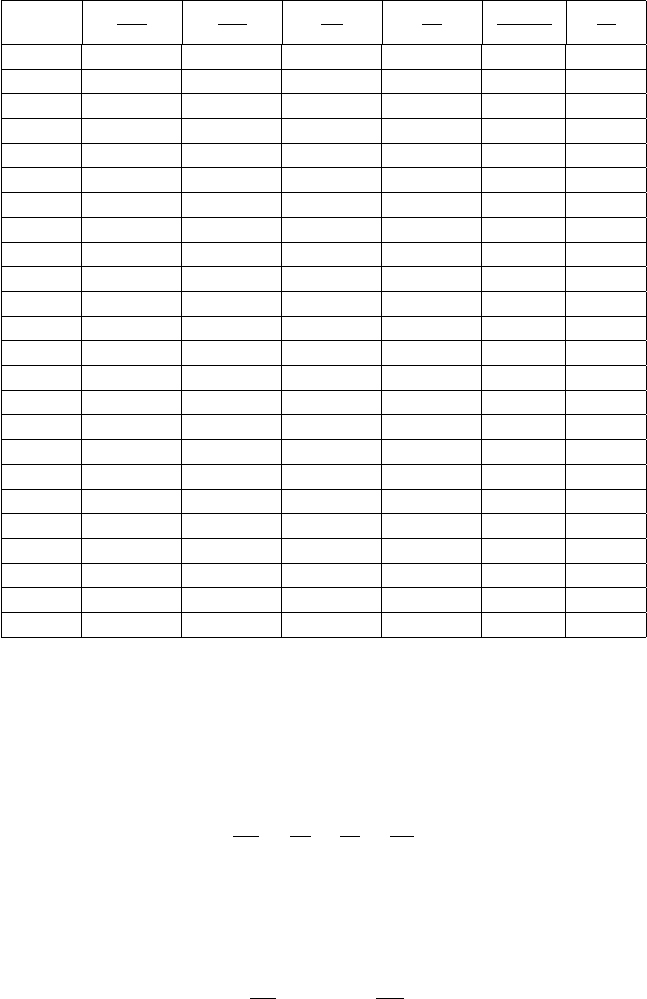
5.5 Isothermal Table

Table -5.3. Isothermal Table

A×P

∗

×P

∗

0.00 0.52828 1.064 5.0E + 5 2.014 1.0E+6 4.2E+5

0.05 0.52921 1.064 9.949 2.010 20.00 8.362

0.1 0.53199 1.064 5.001 2.000 10.00 4.225

0.2 0.54322 1.064 2.553 1.958 5.000 2.200

0.3 0.56232 1.063 1.763 1.891 3.333 1.564

0.4 0.58985 1.062 1.389 1.800 2.500 1.275

0.5 0.62665 1.059 1.183 1.690 2.000 1.125

0.6 0.67383 1.055 1.065 1.565 1.667 1.044

0.7 0.73278 1.047 0.99967 1.429 1.429 1.004

0.8 0.80528 1.036 0.97156 1.287 1.250 0.98750

0.9 0.89348 1.021 0.97274 1.142 1.111 0.98796

1.00 1.000 1.000 1.000 1.000 1.000 1.000

1.10 1.128 0.97376 1.053 0.86329 0.90909 1.020

1.20 1.281 0.94147 1.134 0.73492 0.83333 1.047

5.6. THE EFFECTS OF REAL GASES 87

Table -5.3. Isothermal Table (continue)

A×P

∗

×P

∗

1.30 1.464 0.90302 1.247 0.61693 0.76923 1.079

1.40 1.681 0.85853 1.399 0.51069 0.71429 1.114

1.50 1.939 0.80844 1.599 0.41686 0.66667 1.153

1.60 2.245 0.75344 1.863 0.33554 0.62500 1.194

1.70 2.608 0.69449 2.209 0.26634 0.58824 1.237

1.80 3.035 0.63276 2.665 0.20846 0.55556 1.281

1.90 3.540 0.56954 3.271 0.16090 0.52632 1.328

2.00 4.134 0.50618 4.083 0.12246 0.50000 1.375

2.50 9.026 0.22881 15.78 0.025349 0.40000 1.625

3.000 19.41 0.071758 90.14 0.00370 0.33333 1.889

3.500 40.29 0.015317 7.5E + 2 0.000380 0.28571 2.161

4.000 80.21 0.00221 9.1E + 3 2.75E−5 0.25000 2.438

4.500 1.5E + 2 0.000215 1.6E + 5 1.41E−6 0.22222 2.718

5.000 2.8E + 2 1.41E−5 4.0E + 6 0.0 0.20000 3.000

5.500 4.9E + 2 0.0 1.4E + 8 0.0 0.18182 3.284

6.000 8.3E + 2 0.0 7.3E + 9 0.0 0.16667 3.569

6.500 1.4E + 3 0.0 5.3E+11 0.0 0.15385 3.856

7.000 2.2E + 3 0.0 5.6E+13 0.0 0.14286 4.143

7.500 3.4E + 3 0.0 8.3E+15 0.0 0.13333 4.431

8.000 5.2E + 3 0.0 1.8E+18 0.0 0.12500 4.719

8.500 7.7E + 3 0.0 5.4E+20 0.0 0.11765 5.007

9.000 1.1E + 4 0.0 2.3E+23 0.0 0.11111 5.296

9.500 1.6E + 4 0.0 1.4E+26 0.0 0.10526 5.586

10.00 2.2E + 4 0.0 1.2E+29 0.0 0.100000 5.875

5.6 The eﬀects of Real Gases

To obtained expressions for non–ideal gas it is commonly done by reusing the ideal gas

model and introducing a new variable which is a function of the gas properties like the

critical pressure and critical temperature. Thus, a real gas equation can be expressed in

equation (4.22). Diﬀerentiating equation (4.22) and dividing by equation (4.22) yields

dρ

(5.116)

Again, Gibb’s equation (5.27) is reused to related the entropy change to the change

in thermodynamics properties and applied on non-ideal gas. Since ds = 0 and utilizing

the equation of the state dh = dP/ρ. The enthalpy is a function of the temperature

and pressure thus, h = h(T, P ) and full diﬀerential is

dh =

∂h

∂T

dT +

∂h

∂P

dP (5.117)

88 CHAPTER 5. ISENTROPIC FLOW

The deﬁnition of pressure speciﬁc heat is C

≡

∂h

∂T

and second derivative is Maxwell

relation hence,

∂h

∂P

= v − T

∂s

∂T

(5.118)

First, the diﬀerential of enthalpy is calculated for real gas equation of state as

dh = C

dT −

¶µ

∂z

∂T

(5.119)

Equations (5.27) and (4.22) are combined to form

− z

1 +

¶µ

∂z

∂T

(5.120)

The mechanical energy equation can be expressed as

= −

(5.121)

At the stagnation the deﬁnition requires that the velocity is zero. To carry the inte-

gration of the right hand side the relationship between the pressure and the density has

to be deﬁned. The following p ower relationship is assumed

(5.122)

Notice, that for perfect gas the n is substituted by k. With integration of equation

(5.121) when using relationship which is deﬁned in equation (5.122) results

dP (5.123)

Substituting relation for stagnation density (4.22) results

dP (5.124)

For n > 1 the integration results in

U =

n −1

1 −

(

n−1

)

(5.125)

For n = 1 the integration becomes

U =

(5.126)

5.6. THE EFFECTS OF REAL GASES 89

It must be noted that n is a function of the critical temperature and critical pressure.

The mass ﬂow rate is regardless to equation of state as following

˙m = ρ

∗

(5.127)

Where ρ

∗

is the density at the throat (assuming the chocking condition) and A

∗

is the

cross area of the throat. Thus, the mass ﬂow rate in our properties

˙m = A

∗

z }| {

∗

z }| {

n −1

1 −

(

n−1

)

(5.128)

For the case of n = 1

˙m = A

∗

z }| {

U∗∗

z }| {

(5.129)

The Mach number can be obtained by utilizing equation (4.37) to deﬁned the Mach

number as

M =

√

znRT

(5.130)

Integrating equation (5.120) when ds = 0 results

1 +

¶µ

∂z

∂T

(5.131)

To carryout the integration of equation (5.131) looks at Bernnolli’s equation which is

= −

(5.132)

After integration of the velocity

= −

P/P

(5.133)

It was shown in Chapter (4) that (4.36) is applicable for some ranges of relative

temperature and pressure (relative to critical temperature and pressure and not the

stagnation conditions).

U =

n −1

1 −

n−1

(5.134)

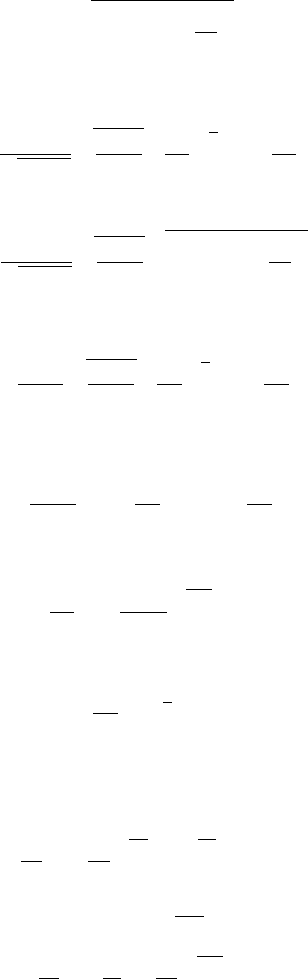
90 CHAPTER 5. ISENTROPIC FLOW

When n = 1 or when n → 1

U =

(5.135)

The mass ﬂow rate for the real gas ˙m = ρ

∗

˙m =

∗

√

n −1

∗

1 −

∗

(5.136)

And for n = 1

˙m =

∗

√

n −1

(5.137)

Fliegner’s number in this case is

F n =

˙mc

∗

n −1

∗

1 −

∗

(5.138)

Fliegner’s number for n = 1 is

F n =

˙mc

∗

= 2

∗

− ln

∗

(5.139)

The critical ratio of the pressure is

∗

n + 1

n−1

(5.140)

When n = 1 or more generally when n → 1 this is a ratio approach

∗

√

e (5.141)

To obtain the relationship between the temperature and pressure, equation (5.131)

can be integrated

[

z+T

(

∂z

∂T

)

]

(5.142)

The power of the pressure ratio is approaching

k−1

when z approaches 1. Note that

1−n

(5.143)