Bar-Meir G. Fundamentals of Compressible Fluid

Подождите немного. Документ загружается.

2.1. BASIC DEFINITIONS 31

This relationship is valid only for ideal/perfect gases.

The ratio of the speciﬁc heats can be expressed in several forms as

k − 1

(2.32)

k R

k − 1

(2.33)

The speciﬁc heat ratio, k value ranges from unity to about 1.667. These values depend

on the molecular degrees of freedom (more explanation can be obtained in Van Wylen

“F. of Classical thermodynamics.” The values of several gases can be approximated as

ideal gas and are provided in Table (2.1).

The entropy for ideal gas can be simpliﬁed as the following

− s

−

ρT

(2.34)

Using the identities developed so far one can ﬁnd that

− s

−

R dP

= C

− R ln

(2.35)

Or using speciﬁc heat ratio equation (2.35) transformed into

− s

k − 1

− ln

(2.36)

For isentropic process, ∆s = 0, the following is obtained

= ln

k−1

(2.37)

There are several famous identities that results from equation (2.37) as

k−1

(2.38)

The ideal gas model is a simpliﬁed version of the real behavior of real gas. The

real gas has a correction factor to account for the deviations from the ideal gas model.

This correction factor referred as the compressibility factor and deﬁned as

Z =

P V

R T

(2.39)

32 CHAPTER 2. REVIEW OF THERMODYNAMICS

2.2 The Velocity–Temperature Diagram

The velocity–temperature (U–T) diagram was developed by Stodola (1934) and ex-

pended by Spalding (1954). In the U–T diagram, the logarithms of temperature is

plotted as a function of the logarithms of velocity. For simplicity, the diagram here

deals with perfect gas only (constant speciﬁc heat)

. The ideal gas equation (2.25) was

described before. This diagram provides a graphical way to analysis the ﬂow and to

study the compressible ﬂow because two properties deﬁnes the state.

The enthalpy is a linear function of the temperature due to the assumptions

employed here (the pressure does not aﬀect the enthalpy). The energy equation (2.18)

can be written for adiabatic process as

h +

= constant

(2.40)

Taking the logarithms of both sides of equation (2.40) results in

log

h +

= constant

(2.41)

log

T +

2 C

= constant

(2.42)

Example 2.1:

Determine the relationship between constant

in equation (2.42) to constant

in equa-

tion 2.40.

Solution

Under construction

End solution

From equation (2.41), it can be observed as long as the velocity square is relatively

small compared to multiplication of the speciﬁc heat by the temperature, it remains close

to constant. Around U

= 2 C

T the velocity drops rapidly. These lines are referred

to as energy lines because kinetic energy and thermal remain constant. These lines are

drawn in Figure 2.1(b).

The sonic line (the speed of sound will be discussed in Chapter 4) is a line that

given by the following equation

U = c =

√

kRT → ln c =

log (kRT ) (2.43)

The reason that logarithms scales are used is so that the relative speed (U/c also

known as Mach number, will be discussed page 54) for any point on the diagram, can

The perfect gas model is used because it provides also the trends of more complicated model.

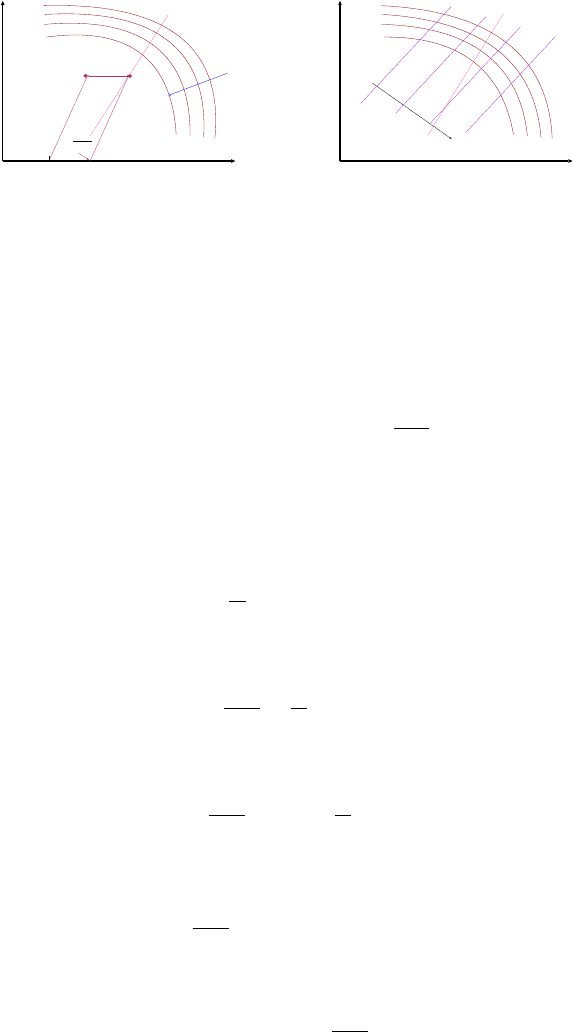
2.2. THE VELOCITY–TEMPERATURE DIAGRAM 33

Log Temperature

Log U

sonic line

Supersonic

flow

Subsonic

flow

Lower Energy

100

M =

1000

(a) Energy Lines eﬀects

Log Temperature

Log U

sonic line

Supersonic

flow

Subsonic

flow

Pressure Lines

Increase Pressure Direction

(b) The pressure lines

Fig. -2.1. Various lines in Velocity–Temperature diagrams

be directly measured. For example, the Mach number of point A, shown in Figure

2.1(a), is obtained by measuring the distance A −B. The distance A − B represent

the ratio of the speed of sound because

A −B = log U|

− log c|

= log

(2.44)

For example, when copying the distance A − B to the logarithms scale results in Mach

number. For instance, copying the distance to starting point of 100, the Mach numb er

at point A will be the read number from the scale divided by 1000.

Mass conservation reads

˙m

= U ρ (2.45)

Subsisting the equation of state (2.25) into equation (2.45) results in

˙m R

A P

(2.46)

Taking the logarithms from both sides results in

log

˙m R

A P

= log

(2.47)

After rearrangement of equation (2.47) obtain

log

˙m R

A P

= log U − log T (2.48)

log T = log U − log

˙m R

A P

(2.49)

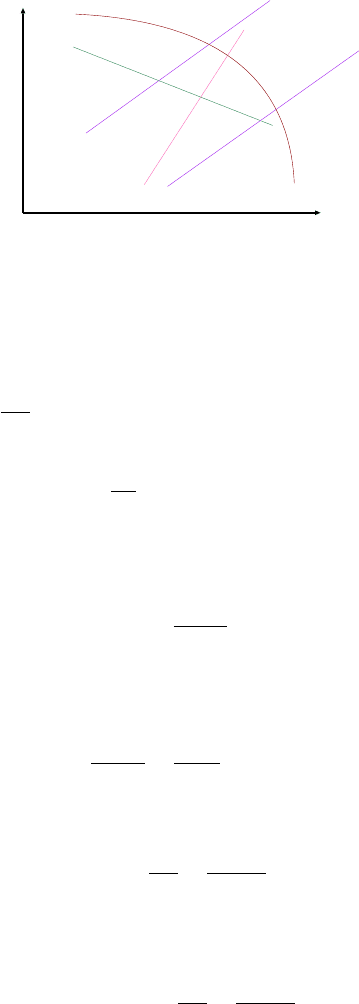
34 CHAPTER 2. REVIEW OF THERMODYNAMICS

Log Temperature

Log U

sonic line

Isentropic line

Pressure line

Fig. -2.2. The ln temperature versus of the velocity diagram

Figure 2.1(b) depicts these lines which referred to as the pressure (mass ﬂow rate) lines.

For constant mass ﬂow and pressure, log T is linearly depend on log U. In fact, for

constant value of log

˙m R

A P

the pressure line is at 45

◦

on diagram.

The constant momentum can be written as

P +

= constant = P

(2.50)

Where P

is the pressure if the velocity was zero. It can be observed that from perfect

gas model and continuing equation the following is obtained

P =

˙m R T

U A

(2.51)

Utilizing the perfect gas state equation and equation (??) and substituting into equation

(2.53) yields

˙m R T

U A

˙m U

A U

= P

(2.52)

Or in simpliﬁed form

T = −

2 R

A U

˙m R

(2.53)

The temperature is upside down parabola in relationship to velocity on the momentum

lines.

log T = log

−

2 R

A U

˙m R

(2.54)

These line also called Stodola lines or Rayleigh lines.

2.2. THE VELOCITY–TEMPERATURE DIAGRAM 35

The maximum of the temp erature on the momentum line can b e calculate by

taking the derivative and equating to zero.

= −

2 U

2 R

˙m R

= (2.55)

The maximum temperature is then

U =

˙m

(2.56)

It can be shown that this velocity is related to

√

where the T

is the velocity zero.

36 CHAPTER 2. REVIEW OF THERMODYNAMICS

CHAPTER 3

Fundamentals of Basic Fluid

Mechanics

3.1 Introduction

This chapter is a review of the fundamentals that the student is expected to know. The

basic principles are related to the basic conservation principle. Several terms will be

reviewed such as stream lines. In addition the basic Bernoulli’s equation will be derived

for incompressible ﬂow and later for compressible ﬂow. Several application of the ﬂuid

mechanics will demonstrated. This material is not covered in the history chapter.

3.2 Fluid Properties

3.3 Control Volume

3.4 Reynold’s Transport Theorem

For simpliﬁcation the discussion will b e focused on one dimensional control volume and

it will be generalzed later. The ﬂow through a stream tube is assumed to be one-

dimensional so that there isn’t any ﬂow except at the tube opening. At the initial time

the mass that was in the tube was m

. The mass after a very short time of dt is dm.

For simplicity, it is assumed the control volume is a ﬁxed boundary. The ﬂow on the

right through the opening and on the left is assumed to enter the stream tube while

the ﬂow is assumed to leave the stream tube.

38 CHAPTER 3. FUNDAMENTALS OF BASIC FLUID MECHANICS

Supposed that the ﬂuid has a property η

= lim

∆t→0

+ ∆t) − N

)

∆t

(3.1)

CHAPTER 4

Speed of Sound

4.1 Motivation

In traditional compressible ﬂow classes there is very little discussion about the speed

of sound outside the ideal gas. The author thinks that this approach has many short-

comings. In a recent consultation an engineer

design a industrial system that contains

converting diverging nozzle with ﬁlter to remove small particles from air. The engineer

was well aware of the calculation of the nozzle. Thus, the engineer was able to predict

that was a chocking point. Yet, the engineer was not ware of the eﬀect of particles on

the speed of sound. Hence, the actual ﬂow rate was only half of his prediction. As it will

shown in this chapter, the particles can, in some situations, reduces the speed of sound

by almost as half. With the “new” knowledge from the consultation the calculations

were within the range of acceptable results.

The above situation is not unique in the industry. It should be expected that

engineers know how to manage this situation of non pure substances (like clean air).

The fact that the engineer knows ab out the chocking is great but it is not enough

for today’s sophisticated industry

. In this chapter an introductory discussion is given

about diﬀerent situations which can appear the industry in regards to speed of sound.

4.2 Introduction

Aerospace engineer, alumni of University of Minnesota, Aerospace Department.

Pardon, but a joke is must in this situation. A cat is pursuing a mouse and the mouse escape

and hide in the hole. Suddenly, the mouse hear a barking dog and a cat yelling. The mouse go out

to investigate, and cat caught the mouse. The mouse asked the cat I thought I heard a dog. The cat

reply, yes you did. My teacher was right, one language is not enough today.

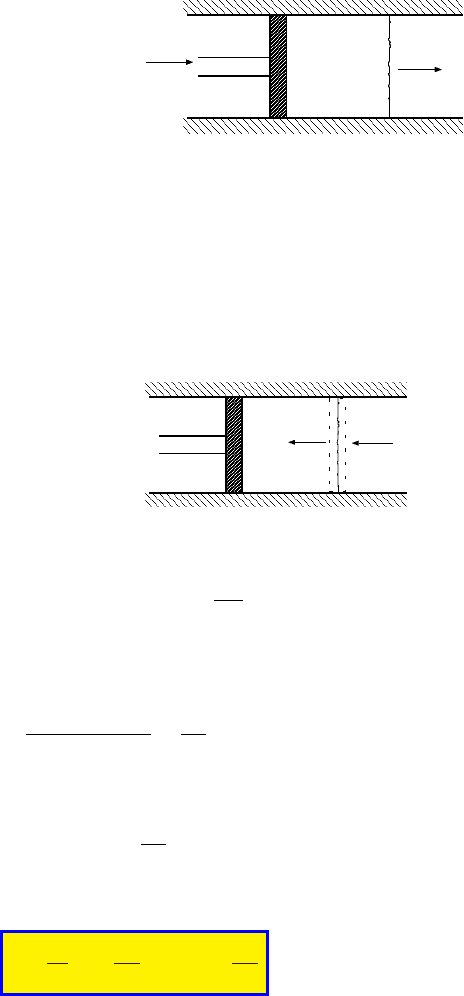
40 CHAPTER 4. SPEED OF SOUND

velocity=dU

P+dP

ρ+dρ

sound wave

Fig. -4.1. A very slow moving piston in a still gas

The people had recognized for several

hundred years that sound is a varia-

tion of pressure. The ears sense the

variations by frequency and magni-

tude which are transferred to the brain

which translates to voice. Thus, it

raises the question: what is the speed

of the small disturbance travel in a

“quiet” medium. This velocity is re-

ferred to as the speed of sound.

To answer this question consider a piston moving from the left to the right at

a relatively small velocity (see Figure 4.1). The information that the piston is moving

passes thorough a single “pressure pulse.” It is assumed that if the velocity of the piston

is inﬁnitesimally small, the pulse will be inﬁnitesimally small. Thus, the pressure and

density can be assumed to be continuous.

c-dU

P+dP

ρ+dρ

Control volume around

the sound wave

Fig. -4.2. Stationary sound wave and gas moves

relative to the pulse.

In the control volume it is

convenient to look at a control volume

which is attached to a pressure pulse.

Applying the mass balance yields

ρc = (ρ + dρ)(c − dU) (4.1)

or when the higher term dUdρ is

neglected yields

ρdU = cdρ =⇒ dU =

cdρ

(4.2)

From the energy equation (Bernoulli’s equation), assuming isentropic ﬂow and ne-

glecting the gravity results

(c −dU )

− c

= 0 (4.3)

neglecting second term (dU

) yield

−cdU +

= 0 (4.4)

Substituting the expression for dU from equation (4.2) into equation (4.4) yields

dρ

=⇒ c

dρ

(4.5)

An expression is needed to represent the right hand side of equation (4.5). For

an ideal gas, P is a function of two independent variables. Here, it is considered that