Бабко Л.В. и др. Теория автоматического управления в примерах и задачах с применением Matlab

Подождите немного. Документ загружается.

Министерство образования Российской Федерации

Санкт-Петербургский государственный технический университет

Л.В.Бабко, В.П.Васильев, В.С.Королев, Н.Д.Тихонов

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

В ПРИМЕРАХ И ЗАДАЧАХ С ПРИМЕНЕНИЕМ ПАКЕТА MATLAB.

Учебное пособие

Санкт-Петербург

2001

УДК 621.078

Теория автоматического управления в примерах и задачах с

применением пакета Matlab. Учебное пособие / Л.В.Бабко, В.П.Васильев,

В.С.Королев, Н.Д.Тихонов / Санкт-Петербургский государственный

технический университет, СПб., 2001.

Пособие предназначено для студентов, обучающихся по направлениям

"Автоматизация и управление" и "Информатика и вычислительная техника".

В каждой главе содержатся краткие теоретические сведения, необходимые

для решения примеров и задач теории линейных непрерывных и дискретных

систем. Решение этих задач, как правило, не требует громоздких вычислений.

Ряд примеров и задач (по указанию преподавателя) могут выполняться с

использованием системы Matlab. Поэтому в отдельной главе приведены

основные функции пакета Control Systems, входящего в Matlab, а также

примеры решения задач.

Рекомендовано к изданию кафедрой автоматики и вычислительной

техники факультета технической кибернетики.

Санкт-Петербургский государственный технический университет, 2001.

Содержание

Введение ...........................................................................................................4

Глава 1. Уравнения и передаточные функции звеньев ..........................................15

Глава 2. Математическое описание систем управления ........................................20

Глава 3. Частотные характеристики систем

автоматического управления ......................................................................25

Глава 4. Устойчивость систем автоматического управления ................................30

Глава 5. Установившиеся режимы САУ ..................................................................35

Глава 6. Переходные процессы в системах

автоматического управления ......................................................................40

Глава 7. Исследование систем управления с использованием Matlab ..................45

7.1. Математические модели линейных систем ................................50

7.2. Преобразование структурных схем .............................................55

7.3. Управляемость, наблюдаемость, минимальность ......................60

7.4. Временные и частотные характеристики ....................................65

7.5. Анализ устойчивости линейных систем .....................................70

7.6. Синтез линейных систем управления .........................................75

7.7. Примеры расчета систем управления .........................................80

7.8. Приложения ...................................................................................90

ЛИТЕРАТУРА ............................................................................................................95

ВВЕДЕНИЕ

Исследование систем автоматического управления состоит из ряда

этапов: составление математического описания отдельных звеньев и всей

системы, анализ устойчивости и установившихся режимов, выбор

корректирующих звеньев и построение переходного процесса. Этот перечень

вопросов и определяет структуру пособия. Большинство приведенных в

пособии задач не требует выполнения громоздких вычислений, поэтому

пособие предназначено, в основном, для использования на практических

занятиях и для самостоятельной работы студентов.

В последнее десятилетие для выполнения многих научных и

инженерных расчетов и, в частности, для автоматизированного проекти-

рования автоматических систем, широко применяются пакеты прикладных

программ, образующих систему Matlab. По указанию преподавателей

примеры и задачи, приведенные в пособии, могут предлагаться для решения

в среде Matlab. Для некоторых из этих задач достаточно использовать

стандартные функции пакета Control Systems, входящего в Matlab. Для

решения более сложных задач приходится составлять свои программы,

которые удобно реализовать в среде Matlab. В последней главе пособия дано

описание основных функций пакета Control Systems с примерами их

применения (применительно к Matlab версии 5.2). В приложении приведены

программы анализа и синтеза линейных систем, которые дополняют

возможности Matlab и могут быть полезны особенно при курсовом

проектировании. Эти программы можно найти в Интернет по адресу:

http://aivt.nord.nw.ru/forstudents/

Глава 1

УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ

В задачах этой главы необходимо составить дифференциальное урав-

нение, связывающее выходную физическую величину y с входной величи-

ной x, используя для этого соответствующие законы физики. В общем случае

полученное дифференциальное уравнение вида:

F( y

(n)

, y

(n-1)

,…, y

′

, y, x

(m)

, x

(m-1)

,…, x

′

, x)=0

является нелинейным. Если функция F и ее первые частные производные по

всем аргументам непрерывны в точке линеаризации (рабочей точке), то ли-

неаризованное уравнение в приращениях записывается в виде:

∆

(n)

+ a

n-1

∆

(n-1)

+…+ a

∆

′

+ a

∆

y = b

∆

(m)

+ b

m-1

∆

(m-1)

+…+ b

∆

′

+ b

∆

где коэффициенты a

и b

равны значениям соответствующих частных произ-

водных при подстановке значений аргументов в точке линеаризации (задают-

ся значения входной и выходной величин и всех их временных производных,

кроме старшей производной выходной величины, значение которой опреде-

ляется из исходного уравнения):

)i(

∂

;

)k(

∂

−=

, где i = 0, 1,…, n, k= 0, 1, …, m.

Передаточная функция звена определяется как отношение изображения

выходной величины к изображению входной величины при нулевых началь-

ных условиях. Формально передаточную функцию можно получить, заменяя

оператор дифференцирования

d/dt на оператор Лапласа p:

apa...papa

bpb......pbpb

)p(W

++++

−

Задачи

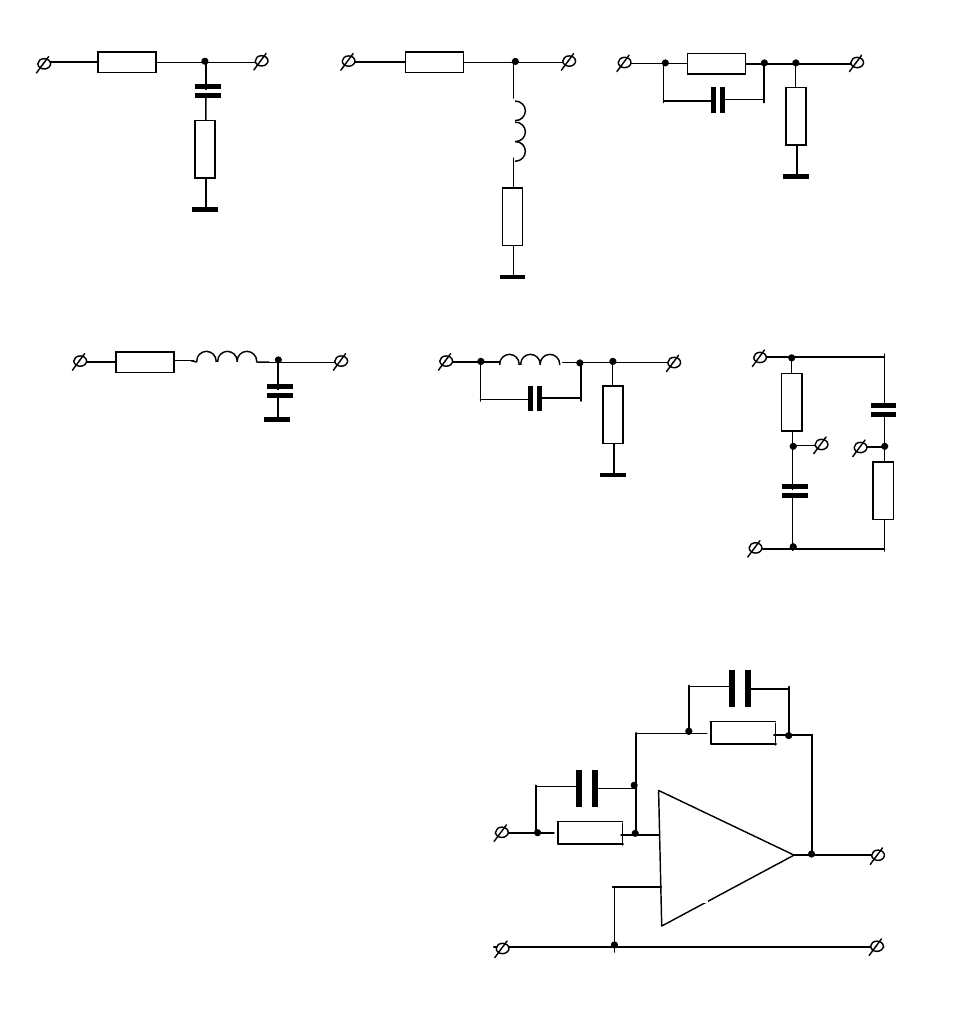
1.1. Составить уравнение и передаточную функцию электрических це-

пей, изображенных на рис. 1.1.

1.2. Составить уравнение и определить передаточную функцию, связы-

вающую выходное напряжение с движка и перемещение движка потенцио-

метра. Длина потенциометра равна

L, сопротивление по длине потенциомет-

ра равномерное. Напряжение питания потенциометра равно

1.3. Составить уравнение движения тела, прикрепленного к неподвиж-

ной стене с помощью пружины, под действием внешней силы

F. Масса

тела – m. Жесткость пружины равна с. На тело действует сила трения, про-

порциональная скорости движения. Коэффициент пропорциональности равен

k. Получить передаточную функцию звена, считая входным воздействием

силу

F, а выходной величиной – координату центра масс тела x.

1.4. Определить передаточную

функцию для цепи с идеальным опе-

рационным усилителем (рис. 1.2).

1.5. Составить уравнение дви-

жения вала с моментом инерции

J под

действием внешнего момента

M. Оп-

ределить передаточную функцию для

двух случаев:

а) входная величина - внешний

момент

M, выходная величина – угло-

вая скорость вращения вала

;

б) входная величина – внешний

момент

M, выходная величина – угол поворота вала

1.6. Составить уравнение, связывающее скорость вращения ротора дви-

гателя постоянного тока (ДПТ)

с входным напряжением якорной цепи U

Момент инерции якоря равен

J, индуктивность и сопротивление якоря – L

, момент вращения пропорционален якорному току с коэффициентом про-

порциональности

, противоЕДС пропорциональна скорости вращения ро-

тора

с коэффициентом пропорциональности С

. (Поток возбуждения по-

стоянен.)

Определить передаточную функцию ДПТ для случаев:

вых

вх

Рис. 1.2.

)

R1 б

)

R1 в

)

г) R1 L д) L е)

Рис.1.1.

а) входная величина – U

, выходная величина –

, момент сопротивле-

ния

= сonst;

б) входная величина – U

, выходная величина – угол поворота ротора

, момент сопротивления М

= сonst;

в) входная величина – момент сопротивления М

, выходная величина –

, U

= сonst.

1.7. Составить уравнение, связывающее якорное напряжение

гене-

ратора постоянного тока с напряжением возбуждения

и скоростью враще-

ния ротора

, считая, что U

пропорционально произведению

и потока воз-

буждения

Ф. Параметры обмотки возбуждения: индуктивность L

и рези-

стивное сопротивление

. Поток возбуждения Ф и ток цепи возбуждения

связаны коэффициентом пропорциональности

. Получить передаточную

функцию для двух случаев:

а) входная величина – U

, выходная величина – U

= сonst;

б) входная величина –

, выходная величина – U

, U

= сonst.

1.8. Составить уравнение химической реакции, если известно, что ско-

рость протекания реакции пропорциональна разности количества непрореа-

гировавшего вещества

x и количества получившегося в результате реакции

продукта

1.9. В резервуар объемом

V, заполненный до краев раствором кислоты

с концентрацией

, втекает раствор той же кислоты с концентрацией

вх

. Ко-

личество раствора, втекающего в резервуар в единицу времени, равно

Q. Ко-

личество раствора, вытекающего из резервуара, равно количеству поступив-

шей жидкости. Считая, что получающийся раствор становится мгновенно

однородным, получить уравнение, связывающее концентрацию раствора в

резервуаре с концентрацией втекающего раствора, и определить передаточ-

ную функцию.

1.10. Составить линеаризованное уравнение:

а) y – x

– x = 0 в точке x

= 1; ж) 0=+

′

yxxyxyy

б)

0sin =−

y x

= 0; 1

0000

′

xyxy ;

в)

0ln =−

y x

= 1; з) 0=

′

yxxxxyy

г) 0cossin =− y

π⁄4

; 1,1,0

0000

=−=

′

xyxy ;

д)

−

y x

= 0; и) 0sin

=++

′

′′

xyxyy

е)

()

−

y x

= 1; 1,0,1

0000

−==

′

xyxy

1.11. Зависимость сопротивления термистора от температуры опреде-

ляется выражением

R = R

-0,1T

; где R

= 10000 Ом, R – сопротивление, Т –

температура в градусах Цельсия. Получить линейную модель термистора,

работающего при

Т = 20°С для малых изменений температуры.

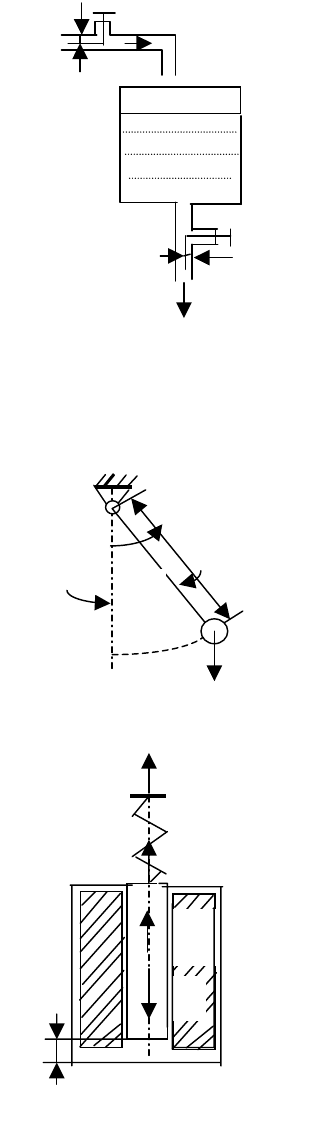
1.12. Составить передаточную функцию звена,

приведенного на рис. 1.3. Количество жидкости, вте-

кающей в единицу времени, пропорционально откры-

тию впускного клапана

. Количество жидкости, выте-

кающей в единицу времени, пропорционально произве-

дению открытия выпускного клапана

и давления

жидкости, т.е. количества жидкости в резервуаре. Ко-

эффициенты пропорциональности –

и с

. Рассмотреть

два случая:

а) входная величина – открытие впускного клапа-

на

, выходная величина – количество жидкости в ре-

зервуаре

Q, x

= x

в0

;

б) входная величина – открытие впускного кла-

пана

, выходная величина – количество жидкости в резервуаре Q при ли-

неаризации в рабочей точке

= x

в0

и x

= x

п0

1.13. Составить уравнение колебаний математиче-

ского маятника (рис. 1.4). Масса маятника равна m, длина

нити –

l. Входной величиной является внешний момент M,

выходной величиной – угол отклонения маятника от вер-

тикальной оси

. Провести линеаризацию полученного

уравнения при

=0 и найти передаточную функцию.

1.14. Составить уравнение движения сердечника

электромагнита (рис. 1.5) массой

m, подвешенного на

пружине с жесткостью

. Электромагнитная сила F

эм

действующая на сердечник, пропорциональна отно-

шению квадрата тока

i, протекающего через катушку,

и величины зазора

. Коэффициент пропорционально-

сти

. Найти передаточную функцию для случаев:

а) входная величина – внешняя сила F

вн

, выход-

ная величина – зазор

, в рабочей точке

при i = i

const

;

б) входная величина – сила тока i, выходная ве-

личина – зазор

, в точке

, i = i

при F

вн

= 0.

1.15. Составить уравнения, описывающие физические процессы, про-

текающие в двигателе постоянного тока при управлении скоростью враще-

ния ротора напряжением возбуждения

. Вращающий момент пропорцио-

Рис. 1.3.

Рис. 1.4.

эм

вн

пр

Рис.1.5.

нален произведению якорного тока

и магнитного потока Ф с коэффициен-

том пропорциональности

мф

, а противоЭДС пропорциональна произведе-

нию скорости вращения ротора

и магнитного потока с коэффициентом

пропорциональности

мф

, магнитный поток пропорционален току в цепи

возбуждения с коэффициентом пропорциональности

. Параметры двигателя

постоянного тока: момент инерции якоря равен

J, индуктивность и сопротив-

ление якоря –

и R

, индуктивность и сопротивление обмотки возбуждения

–

и R

. Определить передаточную функцию двигателя постоянного тока

при управлении со стороны обмотки возбуждения (входная величина –

выходная величина –

, U

= сonst, момент сопротивления М

= сonst) в ра-

бочей точке

а0

, Ф

Глава 2

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ УПРАВЛЕНИЯ

В теории автоматического управления используются два основных

вида описания систем: один – в переменных входы-выходы, другой – в

переменных состояния. Первый приводит к передаточным функциям

(передаточным матрицам) и частотным характеристикам. В этом случае

выходная y и входная u переменные связаны через передаточную функцию:

y=W(p)u. (2.1)

Во втором случае система описывается уравнениями, разрешенными

относительно первых производных переменных состояния.

Состояние непрерывной системы определяется векторной переменной

x(t)=[x

(t), x

(t), ..., x

(t)], позволяющей однозначно определить выход

системы y(t) через ее вход u и начальное состояние x(t)=x(t

Для дискретных систем состояние системы определяется в

фиксированные моменты времени t=kT, (где k=0,1,2 и т.д., T – период

дискретизации или иначе квантования), а x, y и u представляют собой

решетчатые функции x[kT], y[kT] и u[kT] или проще x[k], y[k] и u[k].

Линеаризованные относительно некоторого опорного режима уравнения

состояния имеют стандартный вид:

,Du(t)+Cx(t)=y(t)

,Bu(t) +Ax(t) =(t)x

(2.2)

где A – матрица объекта размерности nxn, B – матрица управления или входа

- nxm, C – матрица выхода – lxn, D – матрица компенсации – lxm. В случаях

m<n матрица D=0.

Соответственно, дискретные системы описываются системой разност-

ных уравнений первого порядка:

Du[k].Cx[k]y[k]

Bu[k], Ax[k]1]x[

+=+

(2.3)

Преобразование уравнений (2.2) к виду (2.1) единственно:

W(p)=C(pE-A)

-1

где E – единичная матрица. Из-за трудностей обращения матриц во многих

случаях передаточную функцию проще получить путем преобразования

структурной схемы, соответствующей уравнениям (2.2).

Переход от уравнений (2.1) к уравнениям состояния (2.2) не является

единственным и зависит от базиса пространства состояний.

Нормальная форма уравнений состояния.

Если система с одним входом управляема и имеет передаточную

функцию вида:

...p

...

)p(W

++++

+++

−