Бабко Л.В. и др. Теория автоматического управления в примерах и задачах с применением Matlab
Подождите немного. Документ загружается.

41
5.6. Определить установившуюся ошибку следящей системы, имеющей
передаточную функцию в разомкнутом состоянии
)p,)(p,(p
)p(
W
1020110
50
1
++
=
при движении задающей оси с постоянной скоростью 0,1 рад/с. Каким
должен быть коэффициент усиления, чтобы скоростная ошибка не
превышала 0,001 рад. ?
5.7. Рассчитать динамическую ошибку, вызванную воздействием на
импульсную систему с единичной обратной связью полиномиального
входного воздействия
x[kt]=a(kT)
2
, a=1 c
-2
, T=0,1. Передаточная функция
разомкнутой системы имеет вид:
.
,z,
z
z,
)z(W
36803681
6320
2
+−
=
5.8.
Передаточная функция разомкнутой следящей системы имеет вид:
)p,)(p,(
p
)p,(
)p(W
1010110
1050100
2
++
+
=
Найти установившуюся ошибку слежения при входном воздействии
x(t)=at
2
,
где
a=5 c
-2
.
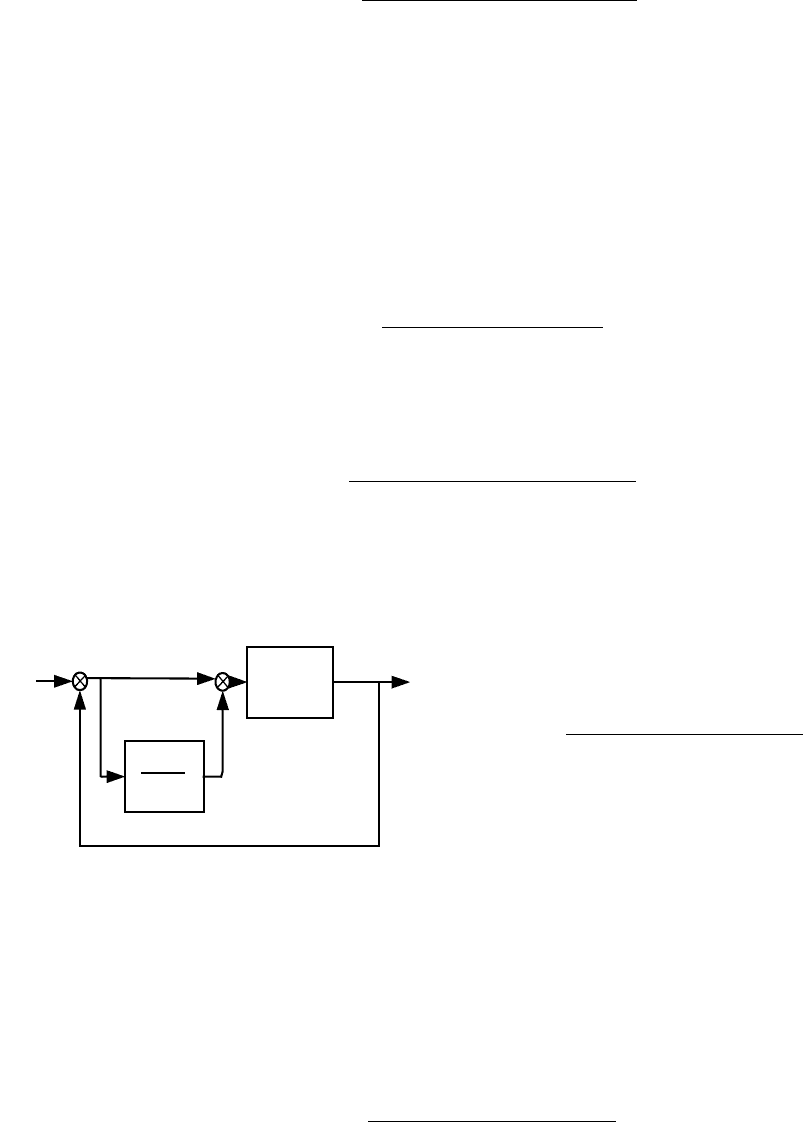
5.9. В закон регулирования
статической системы с передаточной
функцией
)
pT
)(
pT
(
K
)p(W
11
21
++
=
для повышения точности введено
корректирующее воздействие по
интегралу от ошибки (рис. 5.5).
Определить установившуюся ошибку
при отработке входного воздействия
x(t) = a
0
+a
1
t.
5.10. Определить три первых коэффициента ошибок для следящей
системы с передаточной функцией в разомкнутом состоянии
)p
T
)(p
T
(p
K
)p(W
11
21
++
=
Найти выражение для ошибки системы
ε
(t), еcли K=100, T
1
=0,01 c,
T
2
= 0,1 с, и входное воздействие x(t)=a
0
+a
1
t+a
2
t
2
=10+2t-0,5 t
2
.
1
T
и
p
W(p)
g
Y
-
Рис. 5.5

42
5.11. Найти коэффициенты ошибок и выражение
ε
(t) системы,
имеющей передаточную функцию в замкнутом состоянии
p
p
,
p,
p
x
y
)p(W
103051
050
102
23
+++
+
==
при задающем воздействии
x(t)=2+5t+10 t
2
.
5.12. Найти первые два коэффициента ошибок и выражение
ε
(t)
системы, имеющей передаточную функцию в замкнутом состоянии
c. 1 0,Tпри ,
,z,
z
,
x
y
)z(W =
+−
==
6051
10
2
5.13. Передаточная функция разомкнутой системы
.
),z)(z(
z
)z(W
501
2
+−
=
Найти коэффициенты ошибок.
5.14. Передаточная функция разомкнутой следящей системы
)p,(p)Tp(p
K
)p(W
110
20
1 +
=
+
=
На вход системы подается воздействие
x(t) = 2sin(5t). Определить ошибку в
установившемся режиме.
5.15. Для предыдущего примера определить, каким должен быть
коэффициент усиления системы, чтобы ошибка слежения не превышала
ε
m
=6' при гармоническом задающем воздействии с амплитудой x
м
= 10 град.
и частотой
ω= 2 c
-1
.
43
Глава 6
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Зависимость выходной величины от времени аналитически можно по-
лучить различными методами. Классический метод решения линейных диф-
ференциальных или разностных уравнений требует определения корней ха-
рактеристического уравнения (для получения закона собственного движения
системы), определения зависимости выходной величины, соответствующей
входному воздействию (для получения закона вынужденного движения сис-
темы), и вычисления постоянных интегрирования, соответствующих началь-
ным условиям. Применение операторного метода позволяет исключить этап
определения постоянных интегрирования.
При использовании операторного метода сначала определяют изобра-
жение выходной величины, используя преобразование Лапласа для непре-
рывных сигналов: Y(p) = W(p)X(p) и, соответственно, Z-преобразование
Y(z) = W(z)X(z) в случае дискретных. Оригинал Y(t) определяется с помощью
обратного преобразования Лапласа:
[]
∫
==
∞+
∞−
−
j
j
pt
dpe)p(Y
j
)p(YL)t(Y
σ
σ
π
2
1
1
,
и аналогично, оригинал
Y[n] (решетчатая функция) для дискретных систем
вычисляется как обратное Z-преобразование:
[]
∫
=
∫
==
−
+
−
−
dzz)z(Y
j
dpe)e(Y
j
T
)z(YZ]n[Y
n
T/j
T/j
pTpT 11
2
1
2
ππ
πσ
πσ
.
Если изображение непрерывной выходной величины
Y(p) = G(p)/H(p)
или дискретной
Y(z) = G(z)/H(z) представляет дробно-рациональную функ-
цию соответственно от
p или z, то для нахождения оригинала в случае про-
стых полюсов этой функции можно воспользоваться теоремой разложения:
,e
)p(H
)p(G
)t(Y
tp
k
k
k
−
∑
′
=
где p
k
- простой полюс,
k
ppk
dp
dH
)p(H
=
=
′
и соответственно, для дискретных систем:
,
z
)z(H
)z(G
]n[Y
n
k
k
k
1−
∑
′
= где z
k
- простой полюс,
k
zzk
dz
dH
)z(H
=
=
′
.
Вычислить значения оригинала
y[n] в дискретных точках можно без
нахождения полюсов изображения, используя разложение
Y(z) в ряд Лорана.
Из определения Z-преобразования следует:
...z][yz][yz][y][yz]n[y)z(Y
k
n
++
∑
++==
−
∞
=
−−− 3
0
21
3210
Разложив любым способом изображение в ряд Лорана по убывающим
степеням
z: Y(z) = c
0
+c
1
z
-1
+ c
2
z
-2
+ c
3
z
-3
+ … и сравнивая два ряда между со-
бой, можно установить, что
y[0]=с
0
, y[1]= c
1
, y[2]= c
2
, y[3]= c
3
и т.д.

44
Практически ряд Лорана получают делением числителя на знамена-
тель, начиная со старших степеней полиномов.
Качество процессов управления часто оценивается по весовой или пе-
реходной характеристикам.
Весовая характеристика
ϖ
(t) (или
ϖ
[k] для дискретных систем) пред-
ставляет реакцию системы на входное воздействие в виде
δ
(t) (
δ
[k]) при ну-
левых начальных условиях и является оригиналом от передаточной функции:
ϖ
(t) = L
-1
[W(p)] (
ϖ
[k] = Z
-1
{W(z)}).
Переходная характеристика
h(t) представляет реакцию системы на еди-
ничное ступенчатое воздействие при нулевых начальных условиях и равна
=
−
)p(W
p
L)t(h
1
1
. Соответственно, для дискретных систем
−
=
−
)z(W
z
z
Z]n[h
1
1
. Взаимосвязь между весовой и переходной функция-
ми выражается соотношениями:
]k[h]k[и )t(h)t(
.
∇==
ϖϖ
.
Если известна весовая или переходная характеристика, то реакцию сис-
темы на любое входное воздействие
x(t) при нулевых начальных значениях
можно найти с помощью интеграла свертки:
∫
−
′
+=
∫
−=
∞−
tt
d)t(h)(x)(x)t(hd)()t(X)t(Y
0
0
τττττϖτ
,
где
x(0) - значение входного сигнала при t = 0.
Ненулевые начальные значения выходной величины можно заменить
эквивалентными ступенчатыми или импульсными входными сигналами.
Для оценки качества переходного процесса применяются различные
критерии.
В частотных критериях для этой цели используются:
показатель колебательности
М (максимальное значение амплитудной
частотной характеристики замкнутой системы);
резонансная частота
ω
р
, при которой достигается этот максимум;
диапазон положительных частот
ω
п
, в котором значение вещественной
частотной характеристики
U(
ω
) не меньше, чем 0,2U(0);
частота среза
ω
с
, при которой амплитудно-частотная характеристика
разомкнутой системы равна 1.
Из интегральных оценок качества переходного процесса наиболее рас-
пространены квадратичный критерий
[]
dt)(Y)t(Y(I
2
0
2
∫
∞−=
∞
и улучшенный
квадратичный критерий
[]
dtY))(Y)t(Y(I
2
0
222
3
∫
′
+∞−=
∞
τ
. Соотношения,
связывающие значения этих критериев с коэффициентами числителя и зна-
менателя передаточной функции системы, приведены в [1].

45
В корневых критериях оценками качества переходного процесса явля-
ются степень устойчивости
η
= min |
α
i
| и степень колебательности
µ
= max |
β
i
/
α
i
|, где
λ
i
=
α
i
±
β
i
– корни характеристического уравнения систе-
мы. Степень устойчивости
η
позволяет оценить сверху время переходного
процесса:
Т
≤
3/
η
, а степень колебательности
µ
- дать оценку колебательно-
сти всего переходного процесса.
При описании системы в пространстве состояний
Cxy
,BuAxx
=
+
=
&
(для упрощения будем полагать, что система является одномерной, т.е. u и y
– скалярные переменные) изображения Лапласа для переменных состояния x
и выхода y имеют вид:
x(p)=(pE-A)
-1
Bu(p),
y(p)=C(pE-A)
-1
Bu(p).
Вектор состояния как функция времени
.d)(Bue)(xe)t(x
t
)t(AAt
τ
∫
τ+=
τ−
0
0
Выражение Ф(t)=e
At
=L
-1
[(pE-A)
-1
] называется переходной матрицей или мат-
ричной экспонентой. Тогда весовая функция
y(t)=w(t)=L
-1
[C(pE-A)
-1
B]=Ce
At
B=CФ(t)B.
Переходная матрица Ф(t) может быть получена различными способами.
Аналитические способы
:
1) Применением обратного преобразования Лапласа к каждому элемен-
ту матрицы (pE-A)
-1
=(pE-A)
*
/A(p), где (pE-A)* – присоединенная матрица,
A(p)=det(pE-A).
При этом можно использовать формулу разложения и таблицы
преобразования Лапласа.
2) Элементы Ф(t) можно получить по формуле Лагранжа-Сильвестра:
Ф(t) =e
At
=
tp
niiiiii
n|ii
i
e
)pp)...(pp)(pp)...(pp(
|pA|...|pA||EpA|...|EpA|
∑
−−−−
−
−
−
−
+−
+−
111
111
(для случая простых собственных значений p
i
).
Численный способ
. Значения матрицы перехода для фиксированных
моментов времени t получают разложением матричной экспоненты в степен-
ной ряд: e
At
=1+At+(At)
2
/2!+… .
Решение уравнений состояния в фиксированных точках t
k
=kT
(k=0,1,2, …) может быть получено в виде рекуррентного соотношения:
∫
ττ+=+
+
τ−
T)k(
kT
)kT(AAT
,)d)(Bue]k[x(e]k[x
1
1
где e
AT
– матричная экспонента с постоянными коэффициентами, которая
может быть вычислена путем разложения в ряд Тейлора или с использовани-
ем дробно-рациональной аппроксимации, например, вида:
e
AT
=(12E-6TA+T
2
A
2
)
-1
(12E+6TA+T
2
A
2
).
46
Для вычисления интеграла можно воспользоваться методом левых
прямоугольников: ].k[BTud)(Bue
T)k(
kT
)kT(A
=ττ
∫
+
τ−
1
В результате получим x[k+1]=e
AT
(x[k]+BTu[k]).
Корневые методы используются и при синтезе систем автоматического
управления для получения заданного расположения полюсов передаточной
функции. Пусть процессы в системе с одним входом описываются уравнени-
ем состояния:
BuAxx +=
&
(6.1)
Введем в этой системе линейную безынерционную обратную связь по
переменным состояния:
u = Kx. (6.2)
С учетом (6.2) уравнение (6.1) примет вид:
x)B
K
A(x +=
&
(6.3)
Выбирая элементы матрицы обратных связей К, можно получить ха-
рактеристический полином, обеспечивающий требуемое качество переходно-
го процесса. Наиболее просто определить матрицу К в том случае, когда
уравнение (6.1) задано в нормальной форме. Пусть характеристический по-
лином системы (6.1) без обратной связи:
D = p
n
+ а
1
p
n-1
+ … + а
n-1
p + а
n
.
Требуется, чтобы корни характеристического уравнения (6.3) имели
заданные значения
λ
1
,
λ
2
,…,
λ
n
. Тогда характеристический полином матрицы
(А + ВK) замкнутой системы будет иметь вид:
D = (р -
λ
1
)(р -
λ
2
)…(р -
λ
n
) =
*
n
*
n
n*n
apa...pap ++++
−
−
1
1
1
.
Если уравнение (6.1) задано в нормальной форме, то K является векто-
ром-строкой, имеющей вид: K
.|...|
***
1111
aaaaaa
nnnn
−
−
−
=
−−
Если уравнение (6.1) задано не в нормальной форме, то предварительно
следует найти преобразующую матрицу Р перевода (6.1) в нормальную фор-
му (см. главу 2). Затем от вычисленной вектор-строки K
для нормальной сис-
темы можно перейти к вектор-строке K
0
обратных связей для исходной мат-
рицы с помощью того же преобразования: K
0
= PK .
Задачи
Переходные процессы в САУ
6.1. Непосредственным интегрированием найти общее решение диф-
ференциальных и разностных уравнений:
а)
x
yy
=
+
&&
;
б)
x
yy
=
−
&&
;
в)
x
yyy =++ 34
&&&
при
x(t) = a1(t), a = const;

47
г)
x
]
k
[
y
]
k
[
y =
+
+ 2 ;
д)
x
]
k
[
y,
]
k
[
y
=
−
+ 2502 ;
е)
x
]
k
[
y,
]
k
[
y
=
+
+ 2502 ;
ж)
x
]
k
[
y
]
k
[
y
]
k
[
y
=
+++ 342
при
x[k]=a1[k], a = const.
6.2. С помощью формул разложения найти весовые функции систем:
а)
)p)(p,)(p,)(p,(
p
)p(W
1150120110
3
++++
+
= ;
б)
)p(p
pppp
)p(W
1
148
23
234
−
+
+
++
=
;
в)
;
)p()p)(pp(
)p)(p(
)p(W
531
41
22
++++
+
+
=
г)
;
,z,z
,
)z(W
4031
10
2
+−
=
д)
;
,z,z
z
)z(W
5051
2
+−
=
е)
z,z,z
zz
)z(W
5051
12
23
2
+−
++
=
.
6.3. Определить переходные и весовые функции разомкнутых и замк-
нутых систем, если передаточные функции разомкнутых систем имеют вид:
а)
)12,0(
2,1
)(
+
=
pp
pW
; б)
133
29287
)(
23
2
+++
++
=
ppp
pp
pW
.
6.4. Считая, что выходными величинами являются переменные состоя-
ния, определить переходные и весовые матрицы для систем, имеющих урав-
нения состояния:
а)
uxx
uxxx
.
.
22
2
2
21
1
+=
++=
; в)
uxxx
uxxx
.
.
++=
++=
21
2
21
1
242
;
б)
21
2
21
1
2
xxx
uxxx
.
.
+=
++=
; г)
uxx
uxxx
.
.
+−=
++−=
1
2
21
1
3
2
.
6.5. Для системы с матрицей
51
60
−−
=
A найти переходную матрицу
состояния Ф(t).
6.6. Найти закон изменения выходной величины для звена с передаточ-
ной функцией
W(p) = 2/(0,2p+1) при входных воздействиях:
а) x = t+ 0,5t
2
; в) x = e
t
;
48
б) x = sin t; г) x = e
-t
и нулевых начальных условиях.
6.7. Переходная функция системы имеет вид:
а) h(t) = 1/6 – e
-5t
– 5/3e
-3t
– 5/2e
-4t
;
б) h(t) = 5 – e
-2t
– 4cos t –2sin t;
в) h(t) = 1– e
-t
+ e
-2t
sin t.
Определить реакцию системы на входное воздействие x(t) = e
-t
1(t) при
нулевых начальных условиях.
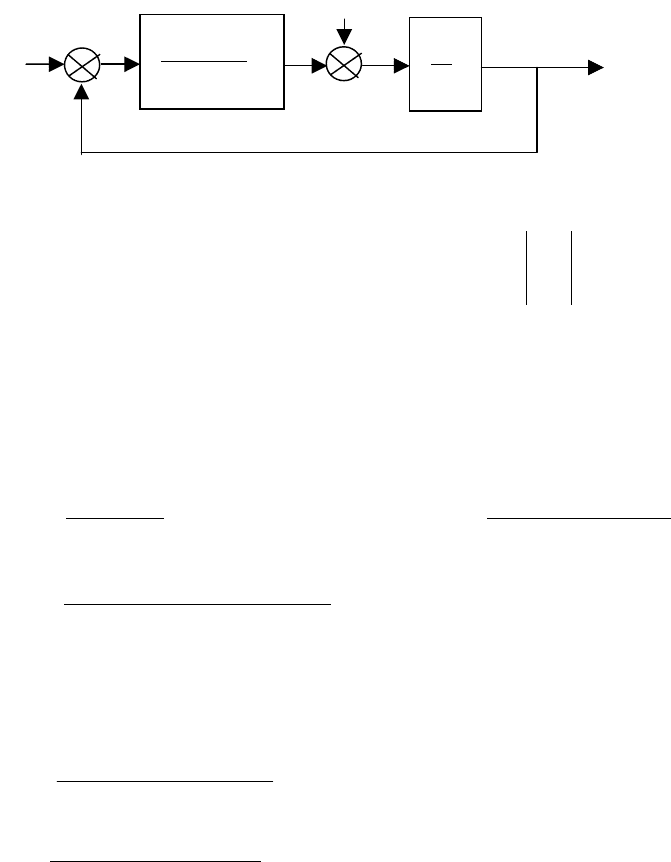
6.8. Определить переходный процесс в следящей системе, структурная
схема которой приведена на рис. 6.1, при нулевых начальных условиях и
входных воздействиях
x(t) = 1(t), f(t) = -1(t).
6.9. Система задана уравнением состояния
xx
00
10
=
&
. Найти матрицу
Ф(t
) и x(t) для начальных условий x
1
(0) = 1; x
2
(0) = 1.
6.10. При каких начальных условиях
)(
0
i
t
y
−=
и отсутствии входного воз-
действия переходный процесс в системе образует весовую характеристику.
Передаточная функция системы имеет следующий вид:
а)
10
0
)(
apa
b
pW
+
=
; б)
21
2
0
10
)(
apapa
bpb
pW
++
+
=
в)
n
nn
m
mm
apapa
bpbpb
pW
+++
+++
=
−
−
....
...
)(
1
10
1
10
.
6.11. Найти изображение выходной величины при отсутствии входного
воздействия и ненулевых начальных условиях для следующих систем:
а)
)pT)(pT(
K
)p(W
11
21
++
=
, y(-0)=y
0
, 0)0(
=
−
y
&
;
б)
papapa
b
pW
2
2
1
3
0
0
)(
++
= , y(-0)=y
0
,
0
)0( yy
&&
=
−
,
0
)0( yy
&&&&
=
−
;
f(t)
Y(t)
x
(t)
11,0
2
+p
p
1
Рис. 6-1
49
в)
32
2
1
3
0
21
2
0
)(
apapapa
bpbpb
pW
+++
++
= , y(-0)=y
0
,
0
)0( yy
&&
=
−
,
0
)0( yy
&&&&
=− .
6.12. Определить передаточные функции систем по заданным выход-
ным процессам y(t) и входным воздействиям x(t). Начальные условия нуле-
вые.
а) y(t) = t
3
, x(t) = t
3
+ 6t;
б) y(t) = 0,25 + e
-t
+ (1,25 –1,5t)e
-2t
, x(t) = e
-t
;
в) y(t) = -0,5e
t
+ 0,5sint + 0,5cost, x(t) = sint;
г) y(t) = 5/9 + 4/3t – 5/9e
-3t
,
x(t) = e
-3t
.
6.13. Определить передаточные функции систем по заданным выход-
ным процессам y(t) и входным воздействиям x(t). Начальные условия ненуле-
вые.
а) y(t) = -5 + 8 e
-3t
+ 12 e
-2t
, x(t) = 2 при y(-0)=7, 0)0( =−y
&
;
б) y(t) = -4 + 12t - e
-t
+ 6e
-2t
, x(t) = 1 - e
-2t
при y(-0)= 1)0( =−y
&
;
в) y(t) = 5/9 + 10/3t – 5/9e
-3t
, x(t) = e
-3t
. при y(-0)= 0, 3)0( =−y
&
.
6.14. Определить изображение и оригинал выходной величины для
системы, имеющей в разомкнутом состоянии передаточную функцию:
а)
)p(p
,
)p(W
1
50
+
=
; б)
)p)(,p(p
p
)p(W
650
58
++
+
=
и начальные условия y(-0) = 10, 000
=
−
=
−
)
(
y
)
(
y
&&&
при ее замыкании
и x(t) = 0.
6.15. Определить, при каких начальных условиях y
(i)
(-0) переходный
процесс в системе, изображенной на рис. 6.1, при воздействиях f(t) = 1(t),
x(t) = 0 будет совпадать с переходным процессом в той же системе при нуле-
вых начальных условиях и воздействиях x(t) =1(t), f(t) = 0.
6.16. При каких условиях, наложенных на функцию Y(p) (порядок по-
линома числителя – m, порядок полинома знаменателя – n), начальные усло-
вия задачи совпадают с начальными значениями оригинала и его l младших
производных.
Косвенные методы оценки качества переходного процесса
6.17. Передаточная функция разомкнутой САУ имеет вид
)Tp(p
K
)p(W
1+
=
. Определить соотношение между K и Т, при котором
сиcтема будет иметь показатель колебательности не более заданного значе-
ния М.

50
6.18. Передаточная функция разомкнутой системы имеет вид
∏
+
=
=
n
i
i
)pT(p
K
)p(W
1
1
. Определить условие, при котором показатель
колебательности замкнутой системы не будет превышать
1 (n – произвольное
число).
6.19. Передаточная функция разомкнутой следящей системы имеет вид
2
1)Tp(p
K
)p(W
+
=
. Вычислить квадратичную интегральную оценку I
2
и оп-
ределить значение
К, соответствующее минимуму I
2
. Найти минимальное
значение
I
2.
6.20. Передаточная функция разомкнутой системы
2
1
p
)Tp(K
)p(W
+
=
.
Вычислить квадратичную интегральную оценку
I
3
для замкнутой системы и
определить значение постоянной времени
Т, соответствующее минимуму
этой оценки.
6.21. Даны характеристические уравнения автоматических систем:
а) р
3
+ 5р
2
+ 8р +6 = 0;
б) р
3
+ 8р
2
+ 19р +12 = 0;
в) р
4
+ 9р
3
+ 46р
2
+ 124р +120 = 0;
г) р
4
+ 6р
3
+ 23р
2
+ 34р +26 = 0.
Определить степень устойчивости
η
и степень колебательности
µ
.
6.22. Передаточная функция разомкнутой системы
)Tp(p
K
)p(W
1+
=
.
Определить степень колебательности
µ
и соотношение между добротностью
к и постоянной времени Т, при котором переходный процесс в замкнутой
системе будет апериодическим.
6.23. Передаточная функция разомкнутой системы
2
1
p
)Tp(K
)p(W
+
=
.
Определить соотношение между
K и Т, при котором в замкнутой системе бу-
дут иметь место:
а) незатухающие колебания; б) апериодический переходный
процесс.
6.24. Передаточная функция объекта управления
2
1
p
)p(W =
.
Определить коэффициенты обратных связей по переменным состояния так,
чтобы полюсы замкнутой системы имели значения –1+j, -1-j.
