Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


502
LINEAR
ALGEBRA
(b) Prove
IIAib
= r
0
(A)
when A
is
Hermitian.
(c)
For
A arbitrary and U unitary of the same order, show
IIA
Uii
2
=
iiUA112
=
IIA112·
28.
Let A be square of order n X
n.
(a) Show that
F(AU)
=
F(UA)
=
F(A),
for any unitary matrix
U.
(b)
If
A
is
Hermitian, then show that
.
F(A)
=
/>.."t_
+ · · ·
+i\~
where i\
1
,
••.
, i\n are the eigenvalues of A, repeated according to their
multiplicity. Furthermore,
29. Recalling the notation of Theorem 7.5, show
F(A)
=
VJLi
+ · · · +
JL;
30. Let A be of order n X
n.
Show
If
A is symmetric and positive definite, show
31. Show that the infinite series
A2
A3
An
I+A+-+-+···+-+···
2!
3!
n!
converges for any square matrix A, and denote the sum
of
the series by eA.
(a)
If
A =
p-
1
BP, show that
eA
=
p-
1
e
8
P.
(b) Let i\
1
,
••.
, i\n denote the eigenvalues of A, repeated according to
their multiplicity, and show that the eigenvalues of
eA are e
1
''1,
•••
,
e.,_•.
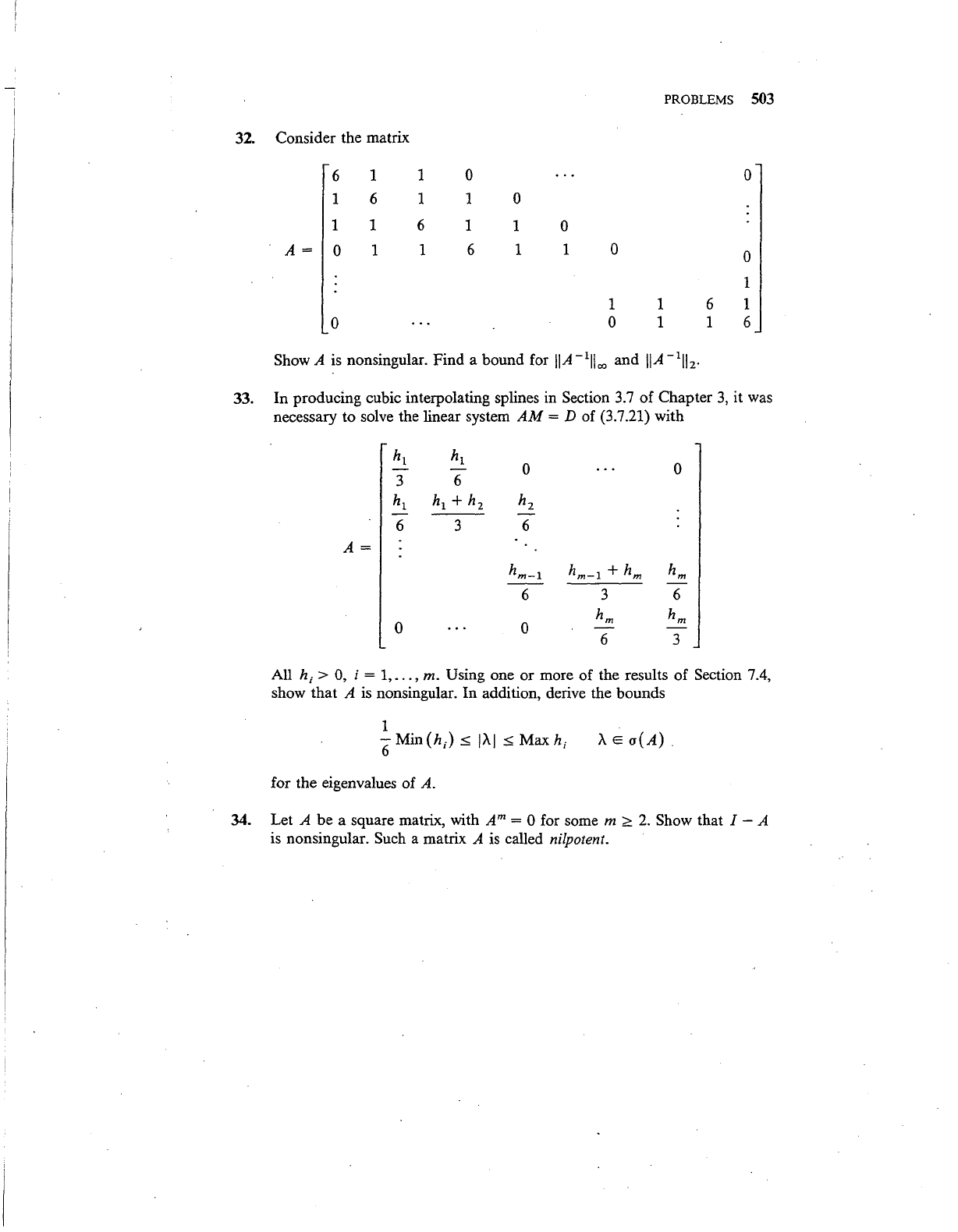
32.
Consider the matrix
6
1
1
1
6 1
1 1 6
A=
0
1
1
0
0
1 0
1
1
0
6
1 1
0
1 1
0 1
PROBLEMS 503
0
0
1
6 1
1 6
Show A is nonsingular. Find a bound for
IIA
-
1
lloo
and
IIA
-
1
llz·
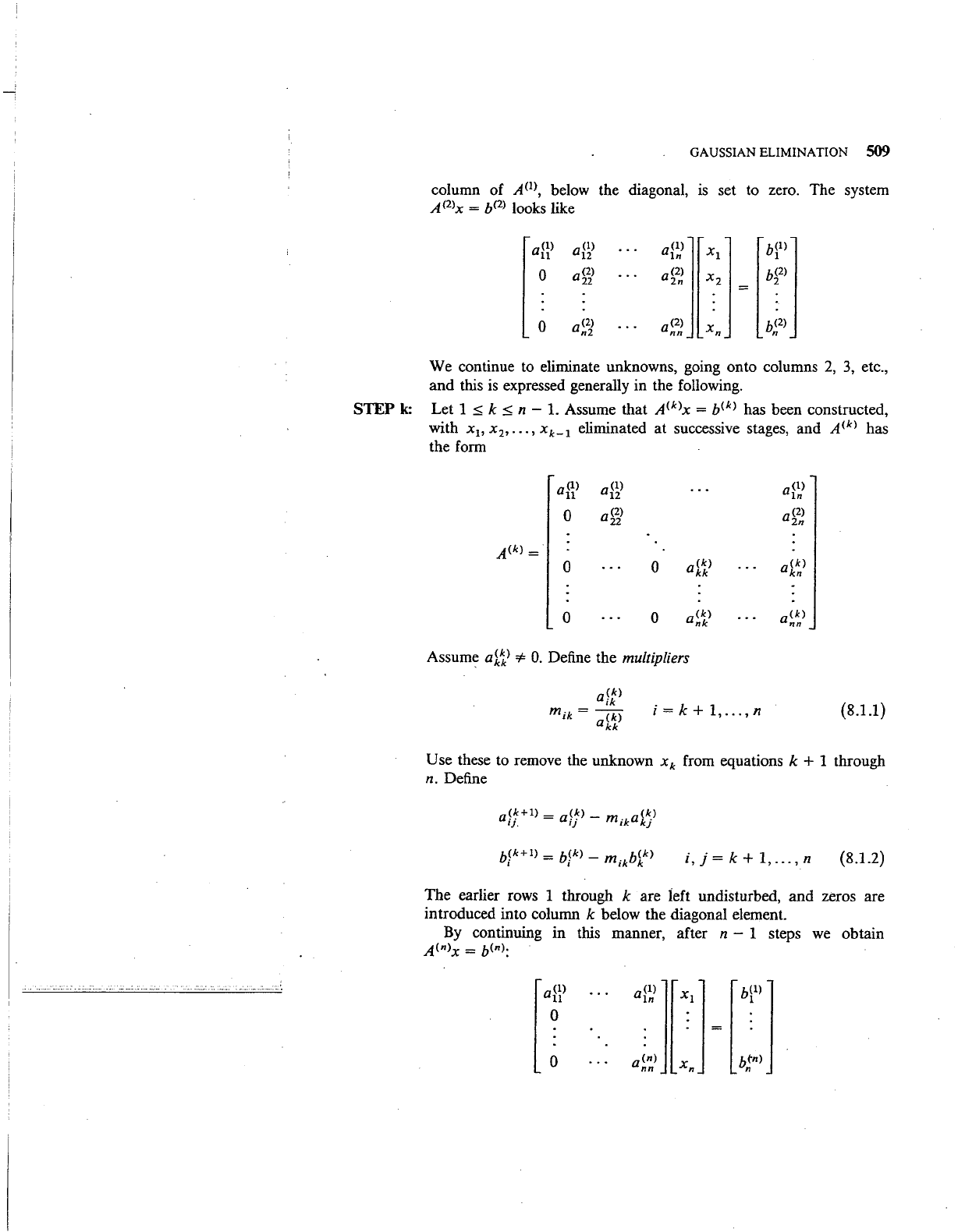
33. In producing cubic interpolating splines in Section 3.7
of
Chapter
3,
it was
necessary to solve the linear system
AM=
D of (3.7.21) with
h1 h1
0
0
- -
3
6
h1
h1
+
h2 h2
- -
6 3 6
A=
hm-1
hm-1
+ hm
hm
6 3 6
0 0
hm
hm
6
3
All
hi
> 0, i = 1,
...
,
m.
Using one
or
more
of
the results
of
Section 7.4,
show
that
A is nonsingular.
In
addition, derive the bounds
A E
a(A)
.
for the eigenvalues
of
A.
34. Let A
be
a square matrix, with Am = 0 for some m
;;:::.
2.
Show that I - A
is nonsingular. Such a matrix A is called nilpotent.

EIGHT

NUMERICAL SOLUTION
OF
SYSTEMS OF LINEAR EQUATIONS
Systems of linear equations arise in a large number of areas, both directly in
modeling physical situations and indirectly in the numerical solution of other
mathematical models. These applications occur in virtually all areas of the
physical, biological, and social sciences. In addition, linear systems are involved
in the following: optimization theory; solving systems of nonlinear equations; the
approximation of functions; the numerical solution of boundary value problems
for ordinary differential equations, partial differential equations, and integral
equations; statistical inference; and numerous other problems. Because of the
widespread importance of linear systems, much research has been devoted to
their numerical solution. Excellent algorithms have been developed for the most
common types of problems for linear systems, and some of these are defined,
analyzed, and illustrated in this chapter.
The most common type of problem
is
to solve a square linear system
Ax=
b
of
moderate order, with coefficients that are mostly nonzero. Such linear systems,
of any order, are called
dense.
For
such systems, the coefficient matrix A must
generally be stored in the main memory of the computer in order to efficiently
solve the linear system, and thus memory storage limitations in most computers
will
limit the order of the system. With the rapid decrease in the cost of computer
memory, quite large linear systems can be accommodated
on
some machines, but
it is expected that for most smaller machines, the practical upper limits on the
order
will
be of size 100 to
500.
Most algorithms for solving such dense systems
are based
on
Gaussian elimination, which
is
defined in Section 8.1.
It
is
a direct
method in the theoretical sense that if rounding errors are ignored, then the exact
answer
is
found in a finite number of· steps. Modifications for improved error
behavior with Gaussian elimination, variants
for special classes of matrices, and
error analyses are given
in Section 8.2 through Section 8.5.
A second important type of problem
is
to
solve
Ax
= b
when:
A is square,
sparse, and
of
large order. A sparse matrix
is
one in which most coefficients are
zero.
Such systems arise in a variety of
ways,
but
we
restrict our development to
those for which there is a simple, known pattern for the nonzero coefficients.
These systems arise commonly in the numerical solution
of
partial differential
equations, and an example is given in Section
8.8.
Because of the large order of
most sparse systems of linear equations, sometimes as large
as
10
5
or more, the
linear system cannot usually be solved by a direct method such
as
Gaussian
507

'
- u
--
-
••
H
---
••
I
508
NUMERICAL SOLUTION
OF
SYSTEMS OF LINEAR EQUATIONS
elimination. Iteration methods are the preferred method
of
solution, and these
are introduced in Section
8.6
through Section 8.9.
For
solving dense square systems
of
moderate order, most computer centers
have a set
of
programs that can be used for a variety
of
problems. Students
should become acquainted with those at their university computer center
and
use
them to further illustrate the material
of
this chapter. An excellent package
is
called
UNPACK.
and it
is
described in Dongarra et al. (1979).
It
is widely
available,
and
we will make further reference to it later in this chapter.
8.1
Gaussian Elimination
This is the formal name given to the method
of
solving systems
of
linear
equations
by
successively eliminating unknowns
and
reducing to systems
of
lower
order.
It
is the method most people learn
in
high school algebra
or
in
an
undergraduate linear algebra course (in which it
is
often associated with produc-
ing the row-echelon form of a matrix). A precise definition is given
of
Gaussian
elimination, which is necessary when implementing
it
on
a computer
and
when
analyzing the effects
of
rounding errors that occur when computing with it.
To
solve
Ax
= b,
we
reduce
it
to
an
equivalent system Ux = g, in which U is
upper triangular. This system can
be
easily solved by a process
of
back-substitu-
tion.
Denote the original linear system by A(llx = b(l),
1:.:;;
i,
j:.:;; n
in which n is the order
of
the system. We reduce the system to
the
triangular
form Ux = g by adding multiples
of
one equation to another equation, eliminat-
ing some unknown from the second equation. Additional row operations are used
in the modifications given in succeeding sections.
To
keep the presentation
simple, we
make
some technical assumptions in defining the algorithm; they are
removed in the next section.
Gaussian elimination algorithm
STEP
1:
Assume
agl
of=
0.
Define the row multipliers by
i =
2,3,
...
, n
These are used in eliminating the x
1
term from equations 2 through n.
Define
a~~l
=
a~~l-
m-
1
a
1
<
1
.l
IJ
lj
I J
i,
j = 2,
...
, n
i = 2,
...
, n
Also, the first rows
of
A and b are left undisturbed,
and
the
first
....
'::.~:.
:.
:·~-
_:
-·
..
:
......
___
-.
GAUSSIAN
ELIMINATION
509
column of A(l>, below the diagonal,
is
set to zero. The system
A<
2
>x
=
b<
2
> looks like
a<I>
11
0
0
a<2>
n2
a<2>
nn
We continue to eliminate unknowns, going onto columns
2,
3,
etc.,
and this
is
expressed generally in the following.
STEP
k:
Let 1
:::::;
k
:::::;
n -
1.
Assume that
A<k>x
=
b<k>
has been constructed,
with
xi, x
2
,
•••
,
xk-I
eliminated at successive stages, and
A<k>
has
the form
a<I>
11
a<ll
12
a<1>
In
0
a<2l
22
a<2l
2n
A<k>
=
a<kl a<kl
0
0
kk
kn
0 0
a<k>
nk
a<kl
nn
Assume
aW
=I=
0.
Define the multipliers
i=k+1,
...
,n
(8.1.1)
Use these to remove the unknown
xk
from equations k + 1 through
n. Define
a(~+I)
=a(~>-
m.
a<k)
1).
IJ
1k
kj
b(k+I) = b(kl _
m.kbk<k>
I I I
i,j=k+1,
...
,n
(8.1.2)
The earlier rows 1 through k are ieft undisturbed, and zeros are
introduced into column
k below the diagonal element.
By
continuing in this manner, after n - 1 steps
we
obtain
A<n>x
=
b(n):
[
a<I>
11
0
0
·:~][7]
=
[br)]
a(n)
X
b(:n)
nn n n

'
..........
.
-
-··
··---
.. ~ -····-·-··
....
-.
"'"
-·-····-·
-·
..........
__
I
510 NUMERICAL SOLUTION
OF
SYSTEMS
OF
LINEAR EQUATIONS
For notational convenience, let U =
A<nl
and g =
b<nl.
The system
Ux
= g
is
upper triangular, and it is quite easy to
so~ve.
First
and
then
k=n-l,n-2,
...
,1
(8~1.3)
This completes the Gaussian elimination algorithm.
Example
Solve the linear system
(8.1.4)
To
simplify the notation,
we
note that the unknowns x
1
,
x
2
,
x
3
never enter into
the algorithm until the
final
step. Thus
we
represent the preceding linear system
with the
augmented matrix
[Alb]=
[
~
-1
2
2
-3
The row operations are performed on this augmented matrix, and the unknowns
are given in the final step. In the following diagram, the multipliers are given next
to an arrow, corresponding to the changes they cause:
u
2 1
~]
[~
2 1
~]
2
3
-2
1
-3
0
mzt=2
-1
1
m
31
=
-1
lm32-}
[Uig]=
[~
2 1
!]
-2
1
0
1.
2
Solving
Ux
= g,
x
3
= 1
x
2
=
-1
x
1
= 1

GAUSSIAN ELIMINATION
511
Triangular factorization of a matrix It
is
conveniept to keep the multipliers
m,j,
since we often want to solve
Ax
= b with the same A
but
a different vector b. In
the computer the elements
afj+
1
>,
j;;;:.::
i, always are stored into the
~torage
for
afj>.
The elements
b~low
the diagonal are being zeroed, and this provides a
convenient storage for the elements
m;j·
Store
m;j
into the space originally used
to store
a;j>
i >
j.
There is yet another reason for looking
at
the multipliers
mij
as the elements
of
a matrix. First, introduce the lower triangular matrix
0
1
0
0
f]
Theorem 8.1
If
L and U are the lower
and
upper triangular matrices defined
previously using Gaussian elimination, then
A
=LU
(8.1.5)
Proof
This proof is basically an algebraic manipulation, making use
of
defini-
tions (8.1.1)
and (8.1.2). To visualize the matrix element (LU);j> use the
vector formula
·
Fori
S.j,
( )
[ ]
ujj
LU
;j=
m,1.,
...
,m,,;_
1
,1,0,
...
,0
0
i-1
""
m
.kak<~>
+ a!9
i..t I J
IJ
k-1
i-1
""
[a!~>-
a!~+
1
>]
+
a!~>
i..t IJ IJ
IJ
k-1
=a!9=a
..
ij
IJ
0

i
I
I
i
.I
512 NUMERICAL SOLUTION OF SYSTEMS OF LINEAR EQUATIONS
Fori>
j,
j-1
= "\'
[a(~l-
a(~+l)]
+
aVl
i..J
1)
lj
1)
k=l
=
a(
1
l
=a
..
I)
1)
This completes the proof.
•
The
decomposition (8.1.5) is
an
important result,
and
extensive use is made
of
it
in developing variants
of
Gaussian elimination for special classes
of
matrices.
But for the moment
we
give only the following corollary.
Corollary With
the
matrices
A,
L,
and U as
in
Theorem 8.1,
Proof
By
the product rule for determinants,
det (A) =
det
(
L)
det ( U)
Since L
and
U are triangular, their determinants are the product
of
their
. diagonal elements. The desired result follows easily, since
det(L)
= 1.
Example
For
the system (8.1.4)
of
the previous example,
L = [ ;
~
~]
-1
t 1
2
-2
0
It
is easily verified that A =
LU.
Also
det(A)
=
det(U)
=
-1.
•
Operation count
To
analyze the number
of
operations necessary to solve
Ax
= b using Gaussian elimination, we will consider separately the creation
of
L
and
U from A, the modification
of
b to
g,
and
finally the solution
of
x.
I.
Calculation
of
L and
U.
At
step 1, n - 1 divisions were used to calculate the
multipliers m;
1
,
2:;:;;
i:;:;;
n. Then
(n
- 1)
2
multiplications
and
(n
- 1)
2
additions were used to create the new elements
afJ>.
We can continue in this

GAUSSIAN ELIMINATION 513
Table 8.1 Operation count for
LU
decomposition of a matrix
Step k Additions
Multiplications Divisions
1
2
(n-
1)
2
(n-
2)
2
(n -
1)
2
n-
1
(n -
2)
2
n-2
n
-1
1
1 1
n(n-
1)(2n-
1)
n(n-
1)(2n-
1)
n(n-
1)
6
6
2
Total
way for each step. The results are summarized
in
Table 8.1.
The
total value
for each
·column was obtained using
the
identities
fj=
p(p+1)
j=l
2
ff
=
p(p
+ 1)(2p +
1)
j~l
6
p?:.1
Traditionally, it is the number
of
multiplications and divisions, counted
together,
that
is used
as
the operation count for Gaussian elimination.
On
earlier computers, additions were much faster than multiplications and
divisions,
and
thus additions were ignored
in
calculating the cost
of
many
algorithms. However, on modern computers, the time
of
additions, multipli-
cations,
and
divisions are quite close
in
size.
For
a convenient notation, let
MD(·)
and
AS(·)
denote the number
of
multiplications
and
divisions,
and
the
number
of
additions and subtractions, respectively, for the computation
of
the quantity in the parentheses.
For
the
LU
decomposition
of
A,
we have
n(n
2
-
1) n
3
·MD(LU)
=
~-
. . 3 3
n(n-
1)(2n-
1)
AS(LU)
=
6 3
The
final estimates are valid for larger values of n . .
2.
Modification
of
b to g =
b<n>:
.
n(n-
1)
MD(g)
=
(n-
1)
+
(n-
2)
+ · · ·
+1
=
--
2
-
n(n-
1)
AS(g)
=
2
3. Solution
of
Ux = g
n(n
+
1)
MD(x)
=
2
n(n
-
1)
AS(x)
=
2
(8.1.6)
{8.1.7)
(8.1.8)
