Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


NUMERICAL
INTEGRATION
In this chapter
we
derive and analyze numerical methods for evaluating definite
integrals.
The
integrals are mainly
of
the form
I(/)=
jbf(x)
dx
(5.0.1)
a
with
(a,
b] finite. Most such integrals cannot
be
evaluated explicitly,
and
with
many others,
it
is often faster to integrate them numerically rather than evaluat-
ing them exactly using a complicated antiderivative
of
f(x).
The
approximation
of
/(f)
is usually referred to as numerical integration
or
quadrature.
There are many numerical methods for evaluating (5.0.1),
but
most can be
made to fit within the following simple framework.
For
the integrand
f(x),
find
an approximating family
Un(x)ln
~
1}
and define
In(/)·=
jbfn(x)
dx
=·1(/n)
(5.0.2)
a
We usually require the approximations fn(x) to satisfy
(5.0.3)
And
the form of each fn(x) should be chosen such
that
J(fn)
Cl!-n
be evaluated
easily.
For
the error,
En(!)=
I(j)-
In(!)=
jb[J(x)-
fn(x)]
dx
.a
lEn(!)
I~
jb!J(x)-
fn(x)jdx
~
(b-
a)llf-
fnlloo
a
{5.0.4)
Most numerical integration methods can be viewed within this framework,
although some
of
them are better studied from some
other
perspective. The one·
class
of
methods that does
not
fit
within the framework are those based
on
extrapolation using asymptotic estimates
of
the error. These are examined in
Section 5.4.
249

i
___
j
250 NUMERICAL INTEGRATION
Most numerical integrals
In(/)
will
have the following
form
when they are
evaluated:
n
In(!)=
L
WJ,nf(xj.J
n
~
1 (5.0.5)
J-1
The coefficients w
1
,
n are called the integration weights or quadrature weights; and
the points
x
1
,n
are the integration nodes, usually chosen in [a, b]. The depen-
dence on
n
is
usually suppressed, writing w
1
and x
1
, although it will be
understood implicitly. Standard methods have nodes and weights that have
simple formulas or else they are tabulated in tables that are readily available.
Thus there is usually no need
to
explicitly construct the functions fn(x) of (5.0.2),
although their role in defining
In(/)
may be useful to keep in mind.
The following example
is
a simple illustration
of
(5.0.2)-(5.0.4), but it
is
not of
the form
(5.0.5).
Example Evaluate
1
ex-
1
I=l--dx
0 X
(5.0.6)
This integrand has a removable singularity at the origin. Use a Taylor series for
ex
[see (1.1.4) of Chapter
1)
to
define fn(x), and then define
1
n
xi-l
I=
1
"-dx
n
£.....
'!
0
j=1
J.
n 1
j"f1
(j!)(j)
For
the error in
In,
use
the Taylor formula (1.1.4) to obtain
xn
f(x)-
fn(x)
=
(n
+
1
)!
e(,
for some 0
·~
~x
~
x. Then
xn
I
- I = 1
1
e(,
dx
n 0
(n
+ 1)!
1 e
----,-----
~
I -
In
~
-:-----:-~---=-
(n
+ 1)!(n +
1)
(n + 1)!(n +
1)
(5.0.7)
(5.0.8)
The .sequence in (5.0.7) is rapidly convergent, and (5.0.8) allows us to estimate the
error very accurately. For example, with
n = 6
I6
= 1.31787037

THE TRAPEZOIDAL RULE AND SIMPSON'S
RULE
251
and from (5.0.8)
2.83 X
10-
5
::;
1-
1
6
::;
7.70 X
10-
5
The true error
is
3.18
X
10-
5
•
For
integrals in which the integrand has some kind of bad behavior, for
example, an infinite value at some point,
we
often will consider the integrand in
the form
!{!)
=
jbw(x)f(x)
dx
a
(5.0.9)
The
bad
behavior
is
assumed to be located in w( x ), called the weight function,
and the function
f(x)
will
be assumed to be well-behaved. For example, consider
evaluating
fo\ln
x)f(x)
dx
for arbitrary continuous functions
f(x).
The framework (5.0.2)-(5.0.4) gener-
alizes easily to the treatment of
(5.0.9). Methods for such integrals are considered
in Sections 5.3 and
5.6.
Most numerical integration formulas are based on defining fn(x) in (5.0.2) by
using polynomial or piecewise polynomial interpolation. Formulas using such
interpolation with evenly spaced node points are derived and discussed in
Sections
5.1
and 5.2. The Gaussian quadrature formulas, which are optimal in a
certain sense and which have very rapid convergence, are given in Section 5.3.
They are based on defining fn(x) using polynomial interpolation at carefully
selected node points that need not
be
evenly spaced.
Asymptotic error formulas for the methods of Sections
5.1 and 5.2 are given
and
discussed in Section 5.4, and some new formulas are derived based on
extrapolation with these error formulas. Some methods that control the integra-
tion error in an automatic
way,
while remaining efficient, are
giveiJ.
in Section 5.5.
Section 5.6 surveys methods for integrals that are singular or ill-behaved in some
sense, and Section
5.7
discusses the difficult task of numerical differentiation.
5.1 The Trapezoidal
Rule
and
Simpson's Rule
We begin our development of numerical integration by giving two well-known
numerical methods for evaluating
(5.1.1)
We analyze and illustrate these methods very completely, and they serve as an
introduction to the material of later sections. The interval
[a,
b]
is
always finite in
this section.
-·
···--··--
-
--
··----------
·----
-----
-.
--·.-
·_:
___________
:
...
--
--
j
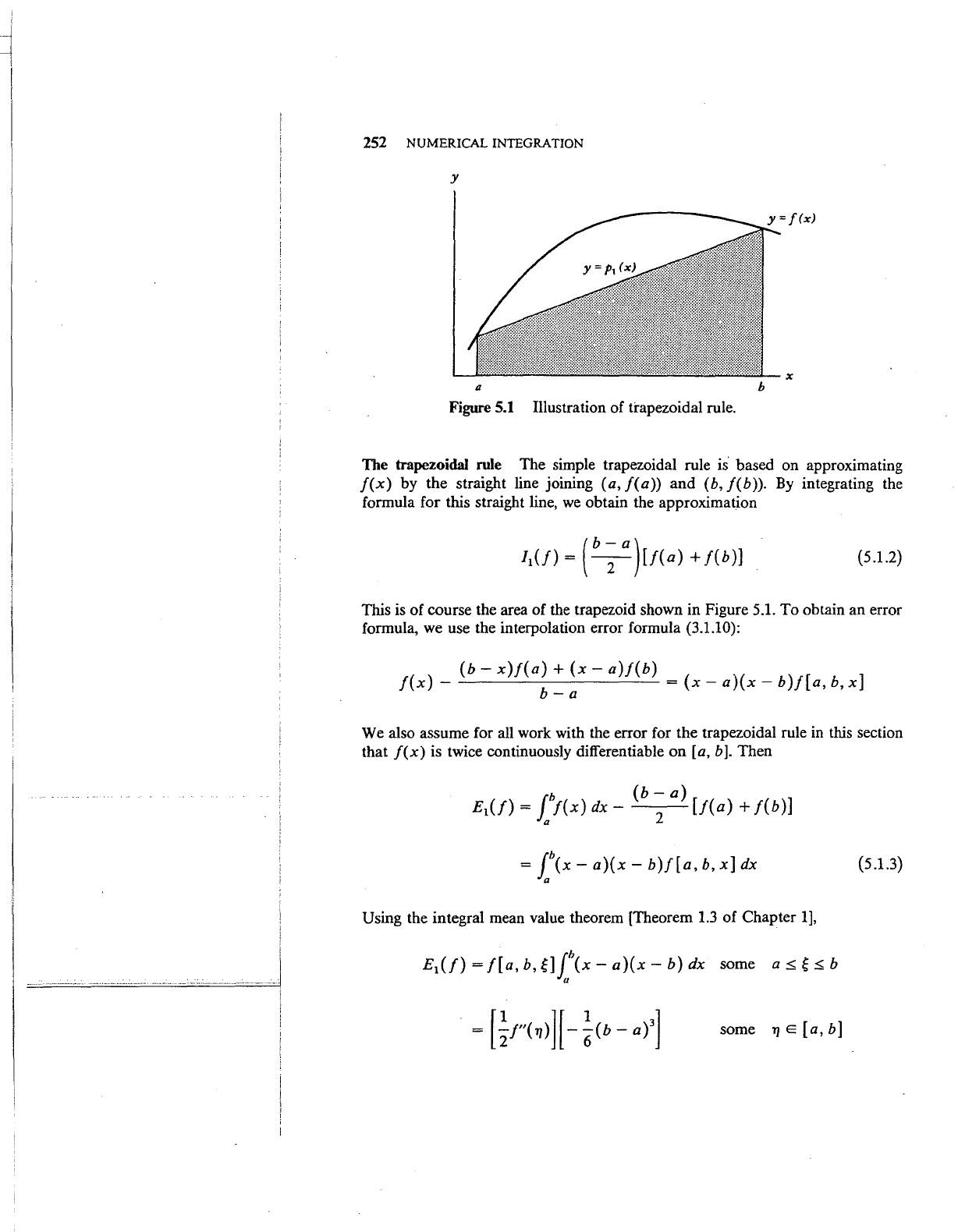
252 NUMERICAL INTEGRATION
y
a b
Figure
5.1
Illustration of trapezoidal rule.
The trapezoidal rule The simple trapezoidal rule is based on approximating
f(x)
by the straight line joining (a,
f(a))
and
(b,
f(b)).
By
integrating the
formula for this straight line,
we
obtain the approximation
(
b-
a)
/1(!)
= -
2
-
[!(a)+
f(b)]
(5.1.2)
This is of course the area of the trapezoid shown in Figure 5.1. To obtain an error
formula, we use the interpolation error formula
(3.1.10):
f(x)-
(b-
x)f(a~
~
~x-
a)f(b)
=
(x-
a)(x-
b)f[a,
b,
x]
We also assume for all work with the error for the trapezoidal rule
in
this section
that
f(x)
is twice continuously differentiable
on
[a, b
].
Then
f
h
(b-a)
£
1
(/)=
f(x)dx-
[J(a)+f(b)]
a 2
=
t(x-
a)(x-
b)f[a,
b,
x]
dx
a
(5.1.3)
Using the integral mean value theorem [Theorem 1.3 of Chapter
1],
£
1
(/)
=
f[a,
b,
~]j\x-
a)(x-
b)
dx some a 5:
~
5:
b
a
some
7J
E [ a, b]

____
J
THE TRAPEZOIDAL
RULE
AND SIMPSON'S RULE
253
using (3.2.12). Thus
TJE[a,b]
(5.1.4)
If
b - a
is
not sufficiently small, the trapezoidal rule (5.1.2)
is
not of much
use.
For
such an integral,
we
break it into a sum of integrals over small
subintervals, and then
we
apply (5.1.2) to each of these smaller integrals. Let
n
;;:::
1, h =
(b-
a)jn,
and xj
=a+
jh
for j = 0,
1,
...
, n. Then
b n
X·
I(/)=
1 J(x)
dx
=
f:-1'
J(x)
dx
a
j=l
xj-I
with xj_
1
.::;;
TJj.::;;
xj. There
is
no reason why the subintervals [xj_
1
,
x)
must all
have equal length, but it
is
customary to first introduce the general principles
involved in this
way.
Although this is also the customary way in which the
method
is
applied, there are situations in which
it
is desirable to vary the spacing
of the nodes.
The first terms in the sum can be combined
to
give the composite trapezoidal
rule,
n;;:::1
(5.1.5)
with
f(x)
=
h·
For the error in In(f),
n h3
En(/)
=I(/)
-In(/)
=
_[
-
12
/"(
TJj)
j=l
h3n[1"
l
=
--
-
'Lf"(TJ)
12
n
j=l
(5.1.6)
For
the term in brackets,
1 n
Min f"(x).::;; M
=-
L,
J"(TJ).::;;
Max
f"(x)
a:s;x:s;b n
j=l
a:s;x:s;b
Since
f"(x)
is
continuous for
a.::;;
x.::;;
b,
it must attain all values between its
minimum and maximum at some point of
[a,
b); thus
f"(TJ)
= M for some
TJ
E
[a,
b).
Thus
we
can write
some
TJ
E [a,
b]
(5.1.7)

254
NUMERICAL INTEGRATION
Another error estimate can be derived using this analysis. From (5.1.6)
L
. .
En(!)
L. . [ h
~
f ( )]
mut
--
2
-
= liTIIt -
-.
1....
"
1J.
n-+oo
h n-+oo 12 .
1
1
j=
1 n
=
--Limit
L:
r<
TJ
1
)h
12 n-+oo
j=l
Since x
1
_
1
~
71
1
:s;
x
1
,
j =
1,
...
, n, the last sum is a Riemann sum; thus
En(!)
1
fb
1
Limit -
2
-
=--
f"(x)
dx
= -
-[j'(b)-
f'(a)]
n->oo
h 12 a
12
{5.1.8)
(5.1.9)
The term
En(/)
is called an asymptotic error estimate for
En(/),
and is valid in
the sense
of
(5.1.8).
Definition Let
En(/)
be an exact error formula, and let
En(/)
be an estimate
of
it. We say that
En(/)
is
an
asymptotic error estimate for
En(/)
if
{5.1.10)
or
equivalently,
The
estimate in (5.1.9) meets this criteria, based
on
(5.1.8).
The
composite trapezoidal rule (5.1.5) could also have been obtained by
replacing
f(x)
by a piecewise linear interpolating function
fn(x)
interpolating
f(x)
at
the nodes x
0
,
x
1
,
•..
, xn. From here on,
we
generally refer to the
composite trapezoidal rule
as
simply the trapezoidal rule.
Example We use the trapezoidal rule (5.1.9)
to
calculate
{5.1.11)
The true value is
I=
-(e"
+
1)/2
~
-12.0703463164. The values
of
In
are
given in Table 5.1, along with the true errors
En
and the asymptotic estimates
En,
obtained from (5.1.9). Note that the errors decrease by a factor of 4 when n
is
doubled
(and
hence h is halved). This result was predictable from the multiplying

"--- -- ·-·· ----------·-·--·------------··-.
---------·--------------------
------
-----
THE TRAPEZOIDAL RULE AND SIMPSON'S RULE
255
Table
5.1
Trapezoidal
rule
for
evaluating
(5.1.11)
n
Jn
En
Ratio
En
2
-17.389259
5.32
4.20
4.96
4
-13.336023
1.27
4.06
1.24
8
-12.382162
3.12E-
1
4.02
3.10E-
1
16
-12.148004
7.77E-
2
4.00
7.76E-
2 .
32
-12.089742
1.94E-
2
4.00
1.94E-
2
64
-12.075194
4.85E-
3
4.00
4.85E-
3
128
-12.071558
1.21E-
3
4.00
1.21E-
3.
256
-12.070649
3.03E-
4
3.03E-
4
512
-12.070422
7.57E-
5
4.00
7.57E-
5
factor
of
h
2
present in (5.1.7) and (5.1.9); when h is halved, h
2
decreases by a
factor
of
4.
This example also shows that
the
trapezoidal rule is relatively
inefficient when compared with other methods to
be
developed in this chapter.
Using the error estimate
En(/),
we can define
an
improved numerical integra-
tion rule:
CTn(!)
=In(!)+
En(!)
=h[~/o+/1
+
···
+fn-1
+
~fn]-
~~[/'(b)-J'(a)]
(5.1.12)
This is called the corrected trapezoidal rule. The accuracy
of
En(/)
should make
CTn(f)
much more accurate than the trapezoidal rule. Another derivation
of
(5.1.12) is suggested in Problem
4,
one showing that (5.1.12) will fit into the
approximation theoretic framework (5.0.2)-(5.0.4). The major difficulty
of
using
CTn{f)
is
that
/'(a)
and
/'(b)
are required.
Example Apply
CT,{f)
to the earlier example (5.1.11). The results are shown
in-
Table
5.2, together with the errors for the trapezoidal rule, for comparison.
Empirically, the error
in
CTn{f)
is
proportional to h
4
,
whereas it was propor-
tional to h
2
with the trapezoidal rule. A proof
of
this is suggested in Problem
4.
Table 5.2 The
corrected
trapezoidal
rule
for
(5.1.11)
n CT,.(f)
Error
Ratio
Trap Error
2
-12.425528367
3.55E-
1
14.4
5.32
4
-12.095090106
2.47E-
2
15.6
1.27
8
-12.071929245
1.58E-
3
3.12E-
1
16
-12.070445804
9.95E-
5
15.9
7.77E-
2
32
-12.070352543
6.23E-
6
16.0
1.94E-
2
64
-12.070346706
3.89E-
7
16.0
4.85E-
3
128
-12.070346341
2.43E-
8
16.0
1.21E-
3

256
NUMERICAL
INTEGRATION
y
X
a
(a+b)/2
b
Figure
5.2 Illustration of Simpson's rule.
Simpson's
rule
To improve upon the simple trapezoidal rule (5.1.2),
we
use a
quadratic interpolating polynomial
p
2
(f)
to approximate
f(x)
on [a, b]. Let
c =
(a
+ b
)/2,
and define
f
h[(x-
c)(x-
b)
(x-
a)(x-
b)
12
(/)=
a
(a-c)(a-b)f(a)+
(c-a)(c-b)f(c)
(x-a)(x-c)
]
+
(b-
a)(b-
c)f(b)
dx
Carrying
outthe
integration,
we
obtain
b-a
h =
--
(5.1.13)
2
This is called Simpson's
rule.
An illustration is given in Figure 5.2, with the
shaded region denoting the area under the graph
of
y =
h(x).
For
the error, we begin with the interpolation error formula (3.2.11) to obtain
=
jb(x-
a)(x-
c){x-
b
)f[a,
b,
c,
x]
dx
a
(5.1.14)
We cannot apply the integral mean value theorem since the polynomial" in the
J integrand changes sign
at
x = c
=(a+
b)/2.
We will assume
f(x)
is
four times
============-=---=·---='!,
continuously differentiable on
[a,
b] for the work
of
this section on Simpson's
rule. Define ·
w(x) =
jx(t-
a)(t-
c){t-
b)
dt
a

THE TRAPEZOIDAL
RULE
AND
SIMPSON'S RULE
257
It
is
not hard to show that
w(a) = w(b) = 0
w(x) > 0 for
a<
x < b
Integrating
by
parts,
£
2
(/)
=
Jbw'(x)f[a,b,c,x]dX
u
d
=
[w(x)f[a,b,c,x]];:!-Jbw(x)-J[a,b,c,x]dx
u
dx
=
-Jbw(x)f[a,
b,
c,
x, x] dx
a
The
last equality used (3.2.17). Applying the integral mean value theorem and
(3.2.12),
Thus
£
2
(/)
=
-J[a,
b,
c,
E.
~]jbw(x)
dx
a
some a
::5;
~
::5;
b
b-a
h =
--
some
TJ
E [a,
b].
2
TJE[a,b]
(5.1.15)
From
this we see that £
2
(/)
= 0 if
f(x)
is a polynomial
of
degree
::5;
3,
even
though quadratic interpolation is exact only if
f(x)
is a polynomial
of
degree at
most two.
The
additional fortuitous cancellation
of
errors is suggested in Figure
5.2. This results in Simpson's rule being much more accurate than the trapezoidal
rule.
Again
we
create a composite rule.
For
n
~
2 and even, define h =
(b-
a)jn,
x
1
= a +
jh
for j =
0,
1,
...
, n. Then
b
n/2
x2.
I(!)=
1
f(x)
dx = L 1
1
f(x)
dx
u
j=
1
x2j-2
with x
21
_
2
::5;
11
1
::5;
x
21
• Simplifying the first terms in the sum, we obtain the
composite Simpson rule:

I
I
-
..
------. ·-------·
·-
-···
----------------
--
---
. J
'
258 NUMERICAL INTEGRATION
As before,
we
will simply call this Simpson's rule.
It
is
probably the most
well-used numerical integration rule. It
is
simple, easy to
use,
and reasonably
accurate for a wide variety of integrals.
For
the error, as with the trapezoidal rule,
hs(n/2) 2
"'~
£/l(j)
=
/(f)
- /11(/) = -
~
.
;;
j~l
f'
4
'(lli)
h
4
(b-a)
En(/)·=-
180 /(4)(71)
some
71
E [ a ,
b]
(5.1.17)
We can also derive the asymptotic error formula
(5.1.18)
The proof
is
essentially the same as
was
used to obtain (5.1.9).
Example We use Simpson's .rule (5.1.16) to evaluate the integral (5.1.11),
used earlier as an example for the trapezoidal rule. The numerical results are
given in Table
5.3.
Again, the rate of decrease in the error confirms the results
given by
(5.1.17) and (5.1.18). Comparing with the earlier results in Table 5.1 for
the trapezoidal rule, it
is
clear that Simpson's rule
is
superior. Comparing with
Table
5.2, Simpson's rule
is
slightly inferior,
but
the speed of convergence is the
same. Simpson's rule has the advantage of not requiring derivative values.
Peano kernel error formulas There
is
another approach to deriving the error
formulas, and it does not result in
the
derivative being evaluated at an unknown
point
71·
We first consider the trapezoidal rule.
Assume/'
E
C[a,
b] and that
f"(x)
is
integrable on [a, b]. Then using Taylor's theorem [Theorem 1.4 in
Table 5.3 Simpson's rule for evaluating (5.1.11)
n
/n
En
Ratio
£,
i -11.5928395534
-4.78E-
1
5.59
-1.63
4 -11.9849440198
-8.54E-
2
14.9
-L02E-
1
8
-12.0642089572
-6.14E-
3
15.5
-6.38E-
3
16 -12.0699513233
-3.95E-4
-3.99E-
4
15.9
32
-12.0703214561
-2.49E-
5
16.0
-2.49E-
5
64
- 12.0703447599
-1.56E-
6
16.0
-1.56E-
6
128
-12.0703462191
-9.73E-
8
-9.73E-
8
