Астахова Е.В. Теоретические основы информатики
Подождите немного. Документ загружается.


31
1 СИСТЕМЫ СЧИСЛЕНИЯ
1.1 ОСНОВНЫЕ ПОНЯТИЯ
;
Система счисления — это способ изображения чисел с помощью конечного
множества символов.
В зависимости от способа изображения чисел системы счисления (c/c) делятся на
позиционные и непозиционные.
В позиционной системе счисления количественное значение каждой цифры
зависит от ее места (позиции) в числе.
В непозиционной системе счисления цифры не меняют своего количественного
значения при изменении их расположения в числе.
Количество (Р) различных цифр, используемых для изображения числа в
позиционной системе счисления, называется основанием системы счисления.
S Число, равное основанию системы счисления, записывается только в двух позициях
данной системы.
S Оборудование, необходимое для хранения любого числа от 0 до М, пропорционально
произведению основания системы счисления (p) на количество разрядов (n) в числе: p*n = log
p
M.
Однородность позиционной системы означает, что множества символов,
используемых в данной системе достаточно для представления любого числа.
;
Разряд (позиция) — место для цифры в числе.
;
Разрядность — количество цифр в числе.
S Разряды нумеруются справа налево.
S Каждому разряду соответствует степень основания. Значения цифр лежат в пределах
от 0 до Р-1.
S Для системы счисления с основанием Р максимальная цифра в одном разряде равна
Р-1.
Разделение числа на целую и дробную части имеет смысл только позиционных
системах. В общем случае запись любого смешанного числа в системе счисления с
основанием Р будет представлять собой ряд вида:
{}
алфавитaaaAPa
основаниеaPPaN
nn
n
n
m
kn
np
−=≤≤
−+==
∑
−
−=
,,,,0
1,
21
1
K
,
Нижние индексы определяют местоположение цифры в числе (разряд):
• положительные значения индексов — для целой части числа (к разрядов);
• отрицательные значения индексов — для дробной части числа (m разрядов).
Пример. – 851,12 = – (8*10
2
+ 5*10
1
+ 1*10
0
+ 1*10
-1
+ 2*10
-2
) =
= – (800 + 50 + 1 + 0,1 + 0,02)
Позиционная система счисления — арабская десятичная система.
Непозиционная система счисления — римская.
Максимальное целое число, которое может быть представлено в k разрядах:
1
max
−=
k
PN
Минимальное значащее (не равное 0) число, которое можно записать в m разрядах
дробной части:
m
PN
−
=
min
.
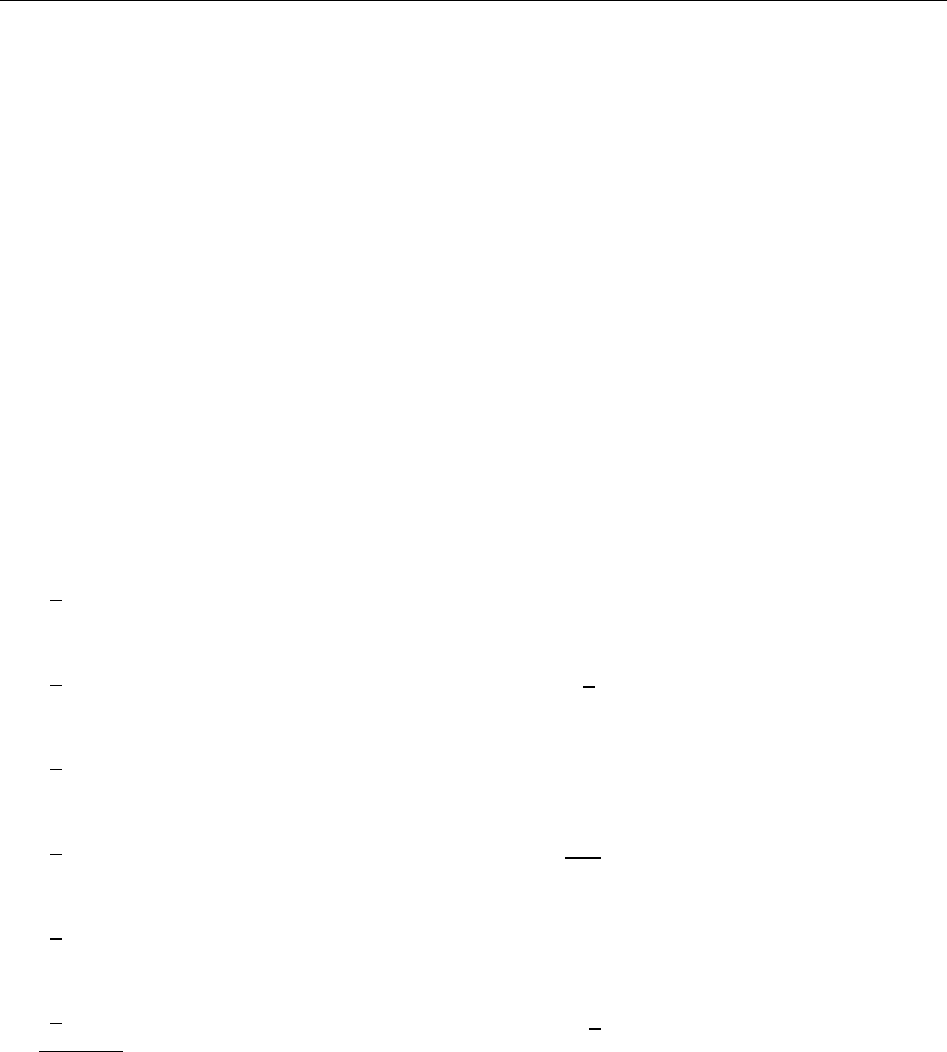
32
Имея в целой части числа k, а в дробной m разрядов, можно записать всего
km
P
+
разных чисел.
Анализ экономичности систем счисления показал, что наиболее эффективными
являются системы с основанием, кратным 2, т.е. 2, 4, 8, 16. В силу специфики построения
схем ЭВМ в современных машинах применяется шестнадцатеричная система счисления.
В одной из первых ЭВМ (ENIAC) использовалась десятичная система счисления.
S Какой цифрой заканчивается четное двоичное число?
1.2 ПЕРЕВОД ЧИСЕЛ
Правило перевода целого числа из системы с основанием p в систему с
основанием d. Делить число и получаемые частные на основание системы d до тех пор,
пока очередное частное не станет меньше d.
Правило перевода правильной дроби. Умножать исходную дробь и дробные части
получающихся произведений на основание системы d. Целые части получающихся
произведений дают последовательность цифр в новой системе (перевод выполняется
приближенно).
Правило перевода смешанного числа. Отдельно переводят целую и дробную
часть, каждую по своим правилам.
Пример 1. Перевод целого числа из десятичной системы счисления в двоичную
11
10
= ?
2
Воспользуемся степенным рядом 8 4 2 1 и представим число 11 как 8 + 2 + 1, что
соответствует наличию в разложении разрядов 1011
2
.
Пример 2. Перевод десятичной
правильной дроби в двоичную
0, 1496
10
= 0, 001001
2
* 2
⎯⎯⎯
0
, 2992
* 2
⎯⎯⎯
0
, 5984
* 2
⎯⎯⎯
1
, 1968
* 2
⎯⎯⎯
0
, 3936
* 2
⎯⎯⎯
0
, 7872
* 2
⎯⎯⎯
1
, 5744
* 2
1, 1488
Пример 3. Перевод двоичной
правильной дроби в десятичную
0, 001001
2
= 0, 1406
10
* 1010
⎯⎯⎯⎯⎯⎯
1001
+ 1001
⎯⎯⎯⎯⎯⎯
1
, 011010
* 1010
1
⎯⎯⎯⎯⎯⎯
11010
+ 11010
⎯⎯⎯⎯⎯⎯
100
, 000100
* 1010
4
⎯⎯⎯⎯⎯⎯
100
+ 100
⎯⎯⎯⎯⎯⎯
0
, 101000
* 1010
0
⎯⎯⎯⎯⎯⎯
101000
+ 101000
⎯⎯⎯⎯⎯⎯

33
110, 010000 6
S Количество различных однобайтовых двоичных кодов равно 2
8
=256 (00000000,
00000001, …, 11111111).
S С помощью одного байта при двоичном кодировании можно представить целое
неотрицательное число от 0 до 255.
S Наибольшее десятичное число, которое можно записать тремя цифрами в двоичной
системе равно 111
2
= 7
10
.
S Наибольшее десятичное число, которое можно записать тремя цифрами в
восьмеричной системе равно 777
8
= 511
10
.
S Наибольшее десятичное число, которое можно записать тремя цифрами в
шестнадцатеричной системе равно FFF
16
= 4095
10
.
Пример 4. Перевод смешанного числа из десятичной системы счисления в
восьмеричную
1996, 55
10
= 3714, 4 (3146)
8
Перевод целой части
Перевод дробной части
0, 55 0, 40 0, 20 0, 60 0, 80
* 8 * 8 * 8 * 8 * 8
⎯⎯ ⎯⎯ ⎯⎯ ⎯⎯ ⎯⎯
4, 40 3, 20 1, 60 4, 80 6, 40
1996
10
⎣8
– 16 249
⎣8
—— – 24 31
⎣8
39 —— – 24
3
– 32 9
⎯
⎯
— – 8 7
76
⎯
—
_72
__ 1
4
S Любая позиционная система счисления дает более компактную запись числа по
сравнению с двоичной.
S
Правила во всех позиционных системах счисления одинаковы.
S
В восьмеричной системе счисления каждая цифра соответствует трем двоичным
разрядам — триаде.
S В шестнадцатеричной системе счисления каждая цифра соответствует четырем
двоичным разрядам — тетраде.
S Если имеется двоичный формат, то восьмеричный и шестнадцатеричный получатся
дроблением справа налево на триады (для 8 = 23) и тетрады (для 16 = 24).
Алгоритм перевода чисел из любой системы счисления в десятичную основан на
представлении числа в форме A
p
= a
n-1
*p
n-1
+ a
n-2
*p
n-2
+ … + a
0
*p
0
+ a
-1
*p
-1
+ a
-m
*p
-m
, где
А — само число, p — основание системы счисления, a
i
— цифры данной системы
счисления, n — количество разрядов целой части числа, m — количество разрядов
дробной части числа.
S Перевести число 11
2
в десятичную систему счисления.
S
Перевести число 11
8
в десятичную систему счисления.
S
Перевести число 11
16
в десятичную систему счисления.
S
Чему равна сумма 11
2
+ 11
8
+11
16
в десятичной системе счисления?
S Последовательность 55
16
, 55
8
, 55
7
упорядочена по убыванию значений, так как
55
16
= 85
10
, 55
8
= 45
10
, 55
7
= 40
10
.
S В какой системе счисления справедливо 21 + 24 = 100?

34
2 СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЭВМ
2.1 ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
В вычислительных машинах применяются две формы представления чисел:
• естественная форма или форма с фиксированной точкой (СФТ)
• нормальная форма или форма с плавающей точкой (СПТ)
Числа СФТ изображаются в виде последовательности цифр с постоянным для всех
чисел положением запятой, отделяющей целую часть от дробной.
Числа (521,377; 0,000238; -102013,036), записанные в разрядную сетку, К = 5, M = 5
+ 00521,37700; + 00000,00238; – 10201,30360.
Эта форма наиболее проста, естественна, но имеет небольшой диапазон
представления чисел и поэтому не всегда приемлема при вычислениях.
Диапазон значащих чисел (N) в системе счисления с основанием Р при наличии k
разрядов в целой части и m разрядов в дробной части числа (без учета знака числа) будет:
,
mkm
PPNP
−−
−≤≤
(при P=2, k=10 и m=6 получим 0,015 ≤ N ≤ 1024)
Если в результате операции получится число, выходящее за допустимый диапазон,
происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В
современных ЭВМ естественная форма представления используется как вспомогательная
и только для целых чисел.
Числа СПТ изображаются в виде двух групп цифр. Первая группа цифр называется
мантиссой, вторая — порядком, причем абсолютная
величина мантиссы должна быть
меньше 1, а порядок — целым числом. В общем виде число в форме с плавающей запятой
может быть представлено так:
r
MPN
±
±= ,
где М — мантисса числа (
|М| < 1); r — порядок числа (r — целое число); P —
основание системы счисления.
S Вещественный формат с m-разрядной мантиссой позволяет абсолютно точно
представлять m-разрядные целые числа.
S Любое целое число может быть без искажений преобразовано в вещественный формат
Мантисса должна быть правильной дробью, у которой первая цифра после запятой
отлична от нуля. При выполнении этого требования число называется нормализованным.
Числа (521,377; 0,000238; -102013,036) в нормальной форме запишутся так:
+ 0,521377*10
3
+ 0,238*10
-3
– 0,102013036*10
5
Нормальная форма представления имеет огромный диапазон отображения чисел и
является основной в современных ЭВМ.
Диапазон значащих чисел в системе счисления с основанием Р при наличии k
разрядов у мантиссы и m разрядов у порядка (без учета знаковых разрядов порядка и
мантиссы) будет:
)1()1(
)1(
−−−−−
−≤≤
mm
PkPk
PPNPP
S При Р = 2, k = 10 и m = 6 диапазон чисел простирается примерно от 10
-19
до 10
19
.
S Чем больше разрядов отводится под мантиссу, тем выше точность представления
числа.
S Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего,
отличного от нуля числа, до наибольшего, представимого в заданном формате.
Знак числа обычно кодируется двоичной цифрой; код 0 означает знак «+», код 1 —
знак «–».

35
При кодированных способах изображения чисел количество разных знаков меньше,
чем количество используемых в системе цифр. Каждая цифра кодируется определенной
комбинацией из нескольких знаков. Так цифры десятичной системы счисления можно кодировать
цифрами двоичной системы. В двоично-десятичной системе каждая цифра кодируется четырьмя
двоичными цифрами.
Двоично-десятичная система счисления получила большое распространение в
современных ЭВМ ввиду легкости перевода в десятичную систему и обратно. Она
используется там, где основное внимание уделяется не простоте технического построения
машины, а удобству работы пользователя. В этой системе счисления все десятичные
цифры отдельно кодируются четырьмя двоичными цифрами и в таком виде записываются
последовательно друг за другом.
Двоичные коды десятичных и шестнадцатеричных цифр
Цифра 0 1 2 3 4 5 6 7 8 9 A B C D E F
Код 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
Десятичное число 9703 в двоично-десятичной системе выглядит так:
1001 0111 0000 0011.
Шестнадцатеричное число F17B в двоичной системе выглядит так:
{
{{
{
B
F
1011011100011111
71
2.2 ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ЭВМ
S Разрядная сетка машины имеет постоянное число разрядов.
При представлении чисел СФТ считают, что точка всегда находится перед
старшим разрядом. Все числа, участвующие в вычислениях по модулю меньше единицы.
Диапазон изменения характеризуется пределами, в которых могут находиться
числа: |X|
max
= 0,111…1 = 1-2
-n
|X|
min
= 0,00…01 = 2
-n
. Числа, выходящие за диапазон
изменения не могут быть представлены в ЭВМ точно.
Ошибка представления числа зависит от величины самого числа и способа
округления. При оптимальном округлении абсолютная ошибка |
ΔX| ≤ 0,5*2
-n
,
относительная ошибка 2
-(n+1)
≤ |δX| ≤ 0,5 (|δX|
min
= |ΔX|/|X|
max
, |δX|
max
= |ΔX|/|X|
min
).
S Для малых чисел ошибка может достигать большой величины.
S Если число меньше минимального, то оно воспринимается как машинный нуль.
S Если число больше максимального, то оно воспринимается как машинная
бесконечность.
Для чисел СПТ абсолютная ошибка равна |ΔX| ≤ 0,5*2
-m
, относительная
|
δX|
min
≈ 2
-(m+1)
, при m — большом, и |δX|
max
= 2
-m
.
S Относительная ошибка для чисел СПТ не зависит от порядка числа.
Единицы измерения объемов информации, хранимой или обрабатываемой в ЭВМ
Количество двоичных
р
азрядов в группе
1
8
8*1024
8*1024
2
8*1024
3
8*1024
4
8*1024
5
Наименование единицы
измерения
Бит Байт Кило-
байт
Мега-
байт
Гига-
байт
Тера-
байт
Пента-
байт
S Биты в числе нумеруются справа налево, начиная с 0-го разряда.
Двоично-кодированные десятичные числа могут быть представлены в ПК полями
переменной длины в упакованном и распакованном форматах.
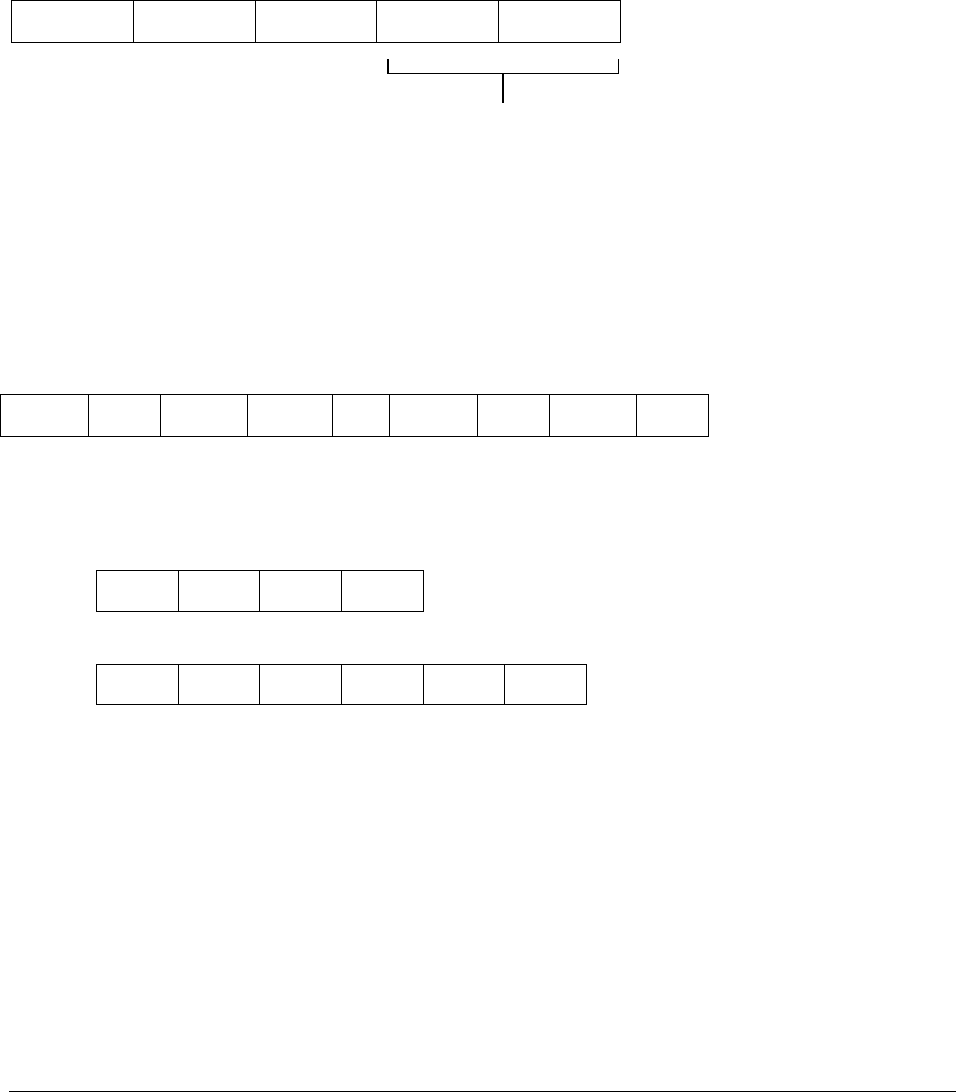
36
Упакованный формат. Десятичной цифре отводится по 4 двоичных разряда
(полбайта); знак числа кодируется в крайнем правом полубайте числа (1100 – знак «+» и
1101 – знак «-»).
Структура поля упакованного формата:
Цифра Цифра
…
Цифра Знак
Упакованный формат используется обычно в ПК при выполнении операций сложения
и вычитания двоично-десятичных чисел.
Распакованный формат. Для каждой десятичной цифры отводится по целому
байту.
Старшие полубайты (зона) каждого байта (кроме самого младшего) заполняются
кодом 0011 (в соответствии с ASCII-кодом). В младших полубайтах кодируются
десятичные цифры. Старший полубайт самого младшего байта используется для
кодирования знака числа.
Структура поля распакованного формата
Зона Цф Зона Цф
…
Зона Цф Знак Цф
Распакованный формат используется при вводе-выводе информации, при
выполнении операций умножения и деления двоично-десятичных чисел.
Пример. Число – 193
10
= – 0001 1001 0011
2-10
а) в упакованном формате
0001 1001 0011 1101
б) в распакованном формате
0011 0001 0011 1001 1101 0011
Распакованный формат является следствием использования в ПК ASCII-кода для
представления символьной информации.
Код ASCII (American Standard Code for Information Interchange — Американский
стандартный код для обмена информацией) имеет основной стандарт и его расширение.
Основной стандарт для кодирования символов использует шестнадцатеричные коды
00–7F, расширение стандарта — 80–FF. Основной стандарт является международным и
используется для кодирования управляющих символов, цифр и букв латинского алфавита;
в расширении стандарта кодируются символы псевдографики и буквы национального
алфавита.
3 АРИФМЕТИЧЕСКИЕ ОСНОВЫ
3.1 ДВОИЧНАЯ АРИФМЕТИКА
Для записи одного и того же числа в различных системах счисления необходимо
различное число разрядов.
S Чем меньше основание системы счисления, тем больше длина числа.
При выборе системы счисления для ЭВМ учитывают, что:
основание системы счисления определяет количество устойчивых состояний, которые
должен иметь элемент ЭВМ (устройство, используемое для изображения разрядов числа);
длина числа существенно зависит от основания системы;
Байт
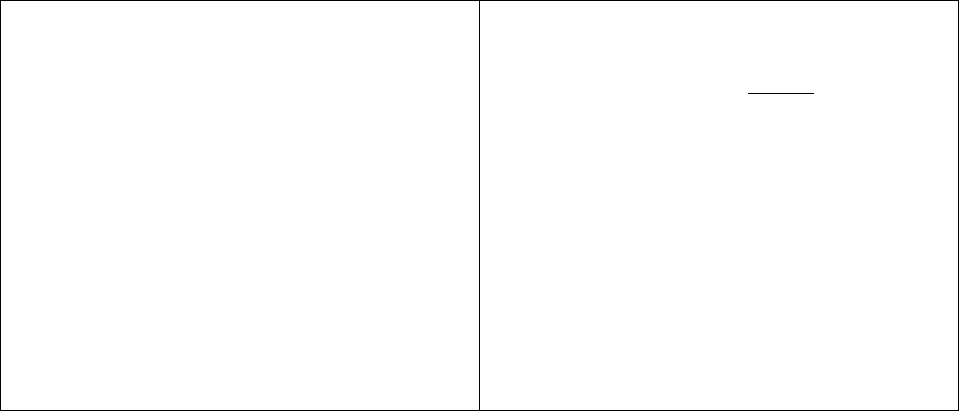
37
система счисления должна обеспечивать простые алгоритмы выполнения
арифметических и логических операций.
Правила выполнения арифметических действий
1 + 0 = 1 1 – 1 = 0 1 * 0 = 0
0 + 1 = 1 1 – 0 = 1 0 * 1 = 0
0 + 0 = 0 0 – 0 = 0 0 * 0 = 0
1 + 1 = 10 0 – 1 = 11 1 * 1 = 1
Умножение многоразрядных чисел осуществляется путем образования частных
произведений и их последующего суммирования.
В двоичной системе умножение сводится к операциям сдвига и сложения, деление —
к операциям вычитания и сдвига.
Пример 1. Умножение в двоичной
системе счисления
11100101, 01
× 101, 1
⎯⎯⎯⎯⎯⎯
1110010101
+ 1110010101
1110010101
⎯⎯⎯⎯⎯⎯⎯
10011101100, 111
Пример 2. Деление в двоичной
системе счисления
1100 1010 1 | 10011
− 10101 — частное
10011
⎯⎯⎯⎯
11001
− 10011
⎯⎯⎯⎯
11001
− 10011
⎯⎯⎯⎯
110 — остаток
Пример 3. Умножение в
восьмеричной системе счисления
345, 2
8
* 5, 4
8
⎯⎯⎯⎯
16250
8
+ 21722
8
⎯⎯⎯⎯
2354, 7
8
Пример 4.
Деление в
восьмеричной системе счисления
625
8
⎣23
8
– 25
8
46
8
⎯⎯
145
8
– 137
8
⎯⎯
6
8
Пример 5. Умножение в
шестнадцатеричной системе счисления
E 5, 4
16
* 5, 8
16
—————
72 A0
+ 47 A4
⎯⎯⎯⎯
4 EC, E0
16
Пример 6. Деление в
шестнадцатеричной системе
счисления
195
16
⎣13
16
− 15
16
13
⎯⎯
65
– 5F
⎯⎯
6
Последовательность вычислений при умножении Е54 на 8

38
1) 4*8=32 2) 32/16=20 20
3) 5*8=40 4) 40/16=28 + 28
5) E=14*8=112 6) 112/16=70 70
————-
7210
0
А
3.2
ПРЯМОЙ, ОБРАТНЫЙ, ДОПОЛНИТЕЛЬНЫЙ КОДЫ
S Положительные числа во всех кодах одинаковы.
Старший разряд регистра — знаковый (0 — «+», 1 — «-»).
S Для кодирования отрицательных чисел и выполнения действий над ними вводят
обратный и дополнительный коды.
Обратный код отрицательного двоичного числа получается, если:
• в знаковый разряд поставить единицу;
• во всех разрядах мантиссы сменить цифры.
Обратный код — инверсия прямого.
Дополнительный код отрицательного двоичного числа получается, если:
• в знаковый разряд поставить единицу;
• во всех разрядах мантиссы сменить цифры;
• к младшему разряду мантиссы прибавить единицу и выполнить переносы, в
том числе в знаковый разряд.
S Дополнительный код = обратный код + 1 в младшем разряде.
S Отрицательное число -2009 в 16-разрядном компьютерном представлении будет
равно …(Ответ: 1111100000100111)
При сложении чисел в обратном коде, складываются все n разрядов, включая
знаковый. В случае возникновения переноса
в знаковом разряде 1 добавляется к
младшему разряду, т.е. выполняется циклический перенос.
При сложении чисел в дополнительном коде складываются все n разрядов,
включая знаковый. В случае возникновения переноса в знаковом разряде 1 не добавляется
к младшему разряду, а отбрасывается.
При сложении в прямом коде не делается перенос из старшего цифрового разряда
в
знаковый.
Если числа разных знаков, то в прямом коде приходится выполнять операцию
вычитания после предварительного сравнения кодов чисел. Результату приписывается знак
большего числа. Эти дополнительные операции приводят к дополнительному усложнению
сумматора.
Пример 1. Сложение обратных кодов чисел.
Сумма обратных кодов равна обратному коду результата.
а)
0, 00100 = [Α]
обр
= А
+
0, 01100 =
[В]
обр
= В
0, 10000 =
[С]
обр
= С
б)
А = – 0, 01001 1, 10110 = [Α]
об
р
+
В = 0, 01110 0, 01110 =
[В]
обр
Выполняется циклический перенос, что
равноценно суммированию с 0, 00001.
1
0, 001 00
0, 00101 =
[С]
обр
= С После циклического переноса.

39
в)
А = – 0, 01100 [Α]
обр
= 1, 10011
+
В = 0, 01001
[В]
обр
= 0, 01001
С = - 0, 00011
1,11100 =
[С]
обр
г)
А = – 0, 01100 1, 10011 = [А]
обр
+
В = – 0, 01001 1, 10110 =
[А]
обр
С = – 0, 10101.
1
1, 01001
1, 01010 =
[С]
обр
Пример 2. Сложение чисел, представленных в дополнительном коде.
Сумма дополнительных кодов есть дополнительный код результата.
а)
0, 01001 = [Α]
доп
= [Α]
пр
+
0, 00101 =
[В]
доп
= [В]
пр
0, 01110 =
[С]
доп
= [С]
пр
б)
А
= – 0, 10010 1, 01110 = [Α]
доп
+
В = 0, 01010 0, 01010 =
[В]
доп
С = – 0, 01000 1, 11000 =
[С]
доп
Нет переноса из мантиссы в знаковый разряд.
в)
А = 0, 10001 = [Α]
доп
= [Α]
пр
+
В = 0, 11111 =
[В]
доп
= [В]
пр
С = 1, 10000
При сложении положительных чисел в результате переноса в знаковом разряде
появилась единица. Результат неверен.
г )
А = – 0, 01001 1, 10111 = [Α]
доп
+
В = 0, 01101 0, 01101 =
[В]
доп
1
0, 00100 = [С]
доп
= [С]
пр
д)
А = – 0, 10001 1, 01111 = [Α]
доп
+
В = - 0, 11010 1, 00110 =
[В]
доп
10, 10101 = [С]
доп
S Доказать, что преобразование отрицательного числа в обратный код выполняется
компьютером быстрее, чем в дополнительный.
S Доказать, что сложение дополнительных кодов выполняется в компьютере быстрее,
чем обратных.
Произошли переносы в знаковый
разряд и из знакового разряда.
Произошел перенос из знакового
разряда. Этот перенос в сумматоре,
работающем в дополнительном коде,
теряется. Получилось
положительное
число. Рез
у
льтат неве
р
ен.
40
3.3 МОДИФИЦИРОВАННЫЕ КОДЫ
Переполнение разрядной сетки возникает в результате сложения чисел, когда
старшие разряды результата не помещаются в отведенной для него области памяти.
S Переполнение разрядной сетки в результате переноса из знакового разряда удобно
обнаруживать в модифицированных кодах.
В модифицированных обратном и дополнительном кодах для кода знака
отводится 2 разряда и знак «-» обозначается 11, а знак «+» — сочетанием 00. Единица
левее знаковых разрядов теряется.
S Сочетания 01 и 10 служат признаком переполнения.
Пример 1. Модифицированный обратный код.
а)
А = 0, 10001 00, 10001=[А]
м
обр
+
В = – 0, 00111 11, 11000=
[В]
м
обр
С = 0,01001
1
00, 01010
В результате циклического переноса из старшего знакового разряда в младший
разряд мантиссы получили положительное число 00, 01001.
б)
А = - 0, 10110 [А]
м
обр
= 11, 01001
+
В = - 0, 01011
[В]
м
обр
= 11, 10100
110
,11101 С учетом циклического переноса
получаем 10, 11110 в знаковом разряде переполнение.
в)
А = - 0, 10010 11, 01101 = [А]
м
обр
+
В = - 0, 01011 11, 10100 =
[В]
м
обр
С = -0,11101 1
11, 00001
С учетом циклического переноса получаем 11,00010
г)
А = 0, 10011 00, 10011 = [А]
м
обр
В = 0, 11001 00, 11001 =
[В]
м
обр
01, 01100 Результат неверен.
Пример 2. Модифицированный дополнительный код.
а)
А = 0, 1010 00, 1010 = [А]
доп. м
.
+
В = - 0, 0101 11, 1011 =
[В]
доп. м.
100, 0101 Единица, расположенная левее двух
знаковых разрядов, отбрасывается, получаем: 00, 0101
б)
А = - 0, 1010 [А]
м
доп.
= 11, 0110
+
В = - 0, 0101
[В]
м
доп.
= 11, 1011
111
, 0001
С учетом потери 1 получаем 11, 0001
+
