Асеева Т.В. Минимизация булевых функций табличными методами
Подождите немного. Документ загружается.


Государственный комитет Российской Федерации по высшей школе
Тверской Государственный Технический Университет
Кафедра электронных вычислительных машин
МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ
ТАБЛИЧНЫМИ МЕТОДАМИ
Методические указания по методам минимизации булевых функций
для студентов специальности 22.01 (Вычислительные машины,
системы, комплексы и сети)
Автор Асеева Т.В.
Тверь 1996
(0-1- -0)
(01-011)
(-101-1)
(----10)
(----0-1)
(-0---1)
(----01-)

Теоретические предпосылки табличных методов минимизации
булевых функций в классе дизъюнктивных нормальных форм
Теоретической основой минимизации булевых функций в классе дизъюнктивных нормальных
форм (ДНФ) является использование правил склеивания, обобщенного склеивания и
поглощения, представляемых формулами:
- Kx Kx = K,
- K
1
x K
2
x = K
1
x K
2
x K
1
K
2
,
- K
1
K
2
K
2
= K
2
,
где К
1
, К
2
, К
3
- элементарные конъюнкции произвольного ранга.
Наиболее известные методы “ручной” минимизации связаны с использованием таблиц
различных видов. Для n-местной булевой функции такая таблица должна содержать 2
n
клеток,
в каждую из которых записывается значение функции на том наборе значений переменных,
номер которого совпадает с номером клетки. Нумерация клеток производится таким образом,
чтобы сделать возможным склеивание клеток, расположенных симметрично относительно
некоторых осей симметрии таблицы. Например, склеиваются любые две соседние по вертикали
или по горизонтали клетки, так как присвоенные им двоичные номера различаются ровно в
одном символе. В склеивании могут участвовать 2
k
клеток, в которых k каких-либо
переменных принимают все возможные наборы значений. Эти к переменных называются
свободными переменными образованного в результате склеивания интервала, который
содержит к свободных и n-k связанных переменных. Интервалу соответствует множество,
содержащее 2
n-k
вершин единичного n-мерного куба В
n
Процесс минимизации в классе дизъюнктивных нормальных форм (ДНФ) сводится к
отысканию максимальных интервалов функции, покрывающих наибольшее число вершин
единичного n-мерного куба, разверткой которого на плоскости и является таблица.
Минимизация булевых функций с использованием диаграмм Вейча
При небольшом числе переменных (n=2,3,4) для минимизации булевых функций используют
диаграммы Вейча
i
. Принцип построения диаграммы и нумерации клеток ясны из рисунков,
Рис. 1,3, 5.
или в двоичной записи:
Рис.1. Нумерация клеток диаграммы Вейча при n=2.
Из рис.1 видно, что, если код номера каждой клетки диаграммы обозначить парой (х
1
,х
2
), то
переменная х
1
принимает значение 1 в клетках с номерами 2 и 3, а переменная х
2
- в клетках с
номерами 1 и 3, что и показано на отмеченой диаграмме Вейча линиями со стрелками. В
приведенной диаграмме могут склеиваться клетки с номерами 0 и 1, а также клетки с номерами
2 и 3 по переменной х
2
, а клетки с номерами 1 и 3 , а также 0 и 2 по переменной х
1
.
Например, для функции двух переменных, заданной таблицей 1, диаграмма Вейча с указанием
клеток, в которых связанная переменная принимает значение 1, и с обозначением склеиваемых
клеток и соответствующих им интервалов приведена на рис.2.
2
3
1
0
10
11
01
00
2
X
1
X
2
(0-1- -0)
(01-011)
(-101-1)
(----10)
(----0-1)
(-0---1)
(----01-)
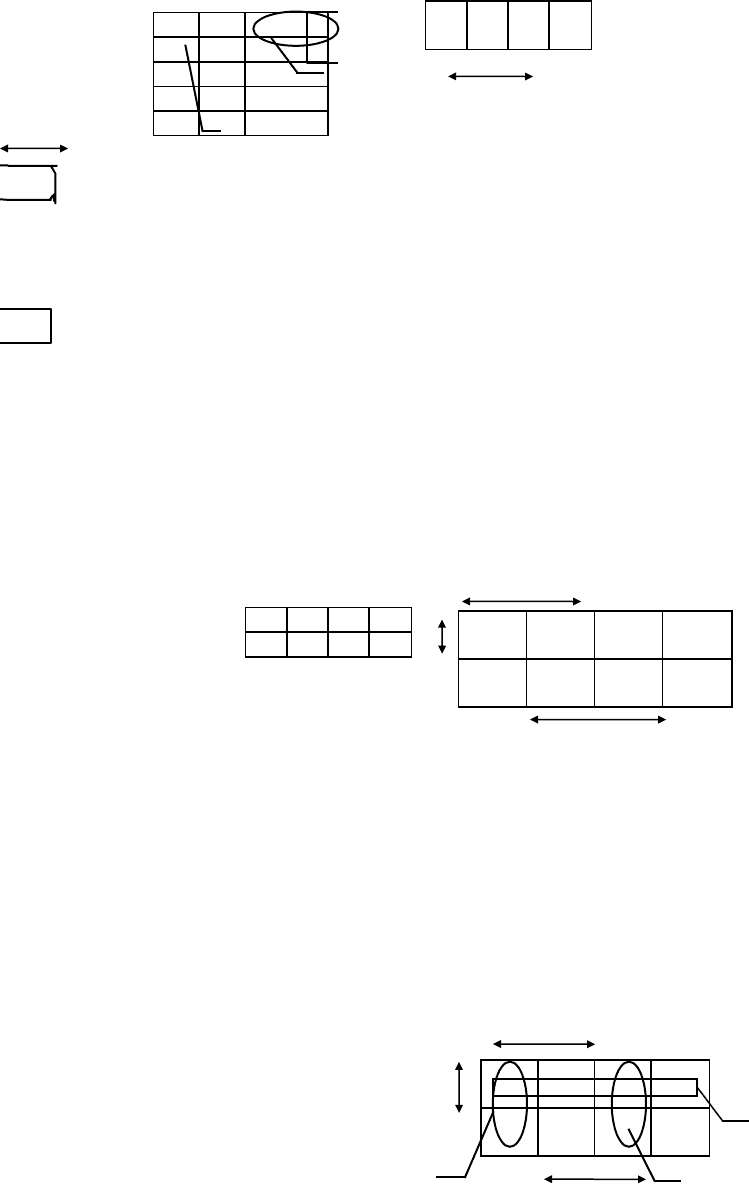
f(x
1
,x
2
)=x
1
x
2
.
Интервалу (0-) соответствует элементарная конъюнкция х
1
, являющаяся простым
импликантом данной функции, а интервалу (-0) - также простой импликант данной функции
х
2
.Таким образом минимальная дизъюнктивная нормальная форма данной функции имеет вид:
f(x)=x
1
x
2
, так как связанная переменная интервала входит в соответствующий ему
импликант с отрицанием, если ее значение в интервале равно 0, и без отрицания в противном
случае.
Для функции трех переменных диаграмма Вейча содержит 2
3
=8 клеток. Нумерация клеток
приведена на рис.3a,b с указанием групп по 2
n-1
клеток, в которых каждая из переменных
принимает значение 1, n - число переменных функции, равное 3.
110 111 011 010
100 101 001 000
Рис. 3.b. Двоичная нумерация клеток
отмеченной диаграммы Вейча
при n=3.
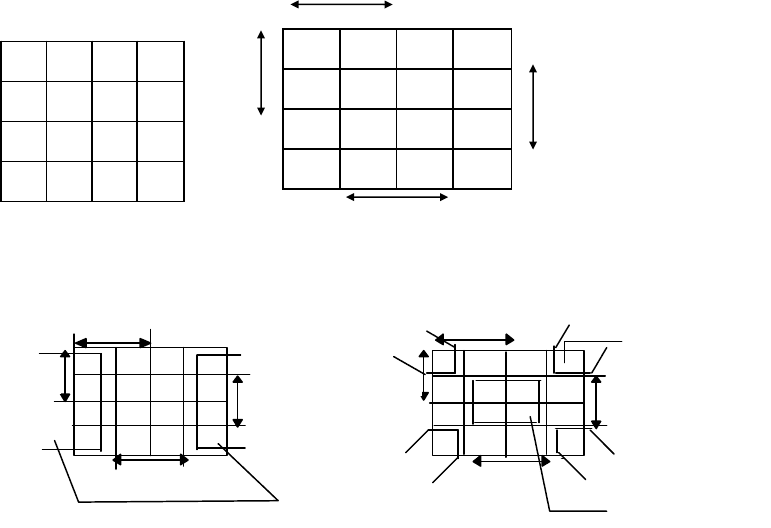
Определим максимальные интервалы и соответствующую МДНФ для функции трех
переменных, заданной вектором
f
=(0111 1011).Изображение этой функции на диаграмме
Вейча показано на рис.4 в предположении, что нумерация переменных в последовательности,
задающей номер клетки, производится слева направо.
Из рис.4 видно, что множество единиц данной функции покрывается тремя максимальными
интервалами, которым соответсвует МДНФ = x
2
x
1
x
3
x
1
x
3
.
1 1 1 1
1 0 1 0
Рис.4. Пример минимизации трехместной булевой функции. Результат минимизации:
f (x
1
,x
2
,x
3
)=x
1
x
2
x
2
x
1
x
3
.
x
1
x
2
f(x
1
,x
2
)
0 0 1
0 1 1
1 0 1
1 1 0
Таблица 1
1 0 1 1
Рис. 2. Пример минимизации
булевой функции, заданной
Табл.1.
6 7 3 2
4 5 1 0
Рис.3,а. Десятичная
нумерация клеток
диаграммы Вейча при
n=3.
3
X
2
(-1-)
(0-)
X
1
X
3
х
2
Х
1
Х
3
(0-1)
(1-0)
(0-1- -0)
x
1
(01-011)
x
2
(-101-1)
(-0)
(----10)
(----0-1)
(-0---1)
(----01-)
Для четырехместной булевой функции таблица содержит 2
4
=16 строк. Соответственно,
диаграмма Вейча такой функции содержит 16 клеток, расположение которых показано на
Рис.5.
1100 1101 1001 1000
1110 1111 1011 1010
0110 0111 0011 0010
0100 0101 0001
0000
0
Рис.5. Нумерация клеток диаграммы Вейча и отмеченная диаграмма при n=4.
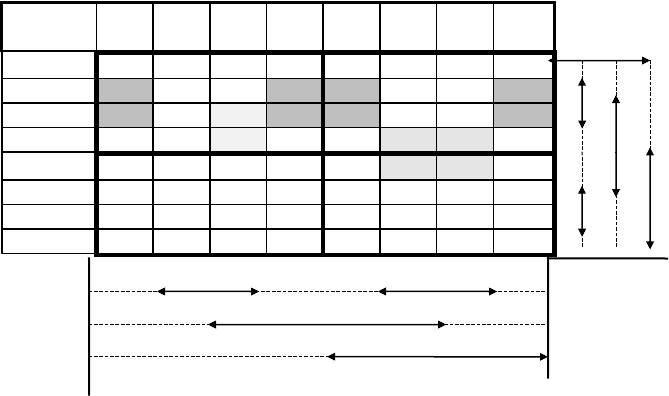
Примеры минимизации 4-х местных булевых функций приведены на рис. 6,7,8.
1 0 0 1
1 0 0 1
1 0 0 1
1 0 0 1
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1
x
2
x
3
x
4
x
1
x
1
x
3
x
4
(---0)
x
2
(--11)
(--00)
f (x
4
)=x
4
f (x
4
)=x
3
x
4
x
3
x
4
Рис.6. Определение МДНФ Рис.7. Определение МДНФ для
функции
для функции, заданной вектором заданной вектором (f)=(1001 1001
1001 1001).
(f)=(1010 1010 1010 1010).
Для четырехместной функции диаграмма Вейча имеет 2
4
=16 клеток. Нумерация клеток и
отмеченная диаграмма приведены на рис.5.
Рис.8. Определение МДНФ для функции, заданной вектором (f)=(1101 110111001101 ).
При дальнейшем увеличении местности булевых функций их минимизация с использованием
диаграмм Вейча становится затруднительной из-за громоздкости таблицы и уменьшения
наглядности ее отметки. Поэтому при n>4 целесообразно использование метода
симметричных таблиц.
Минимизация булевых функций методом симметричных таблиц
Симметричные таблицы обеспечивают наглядность процедуры минимизации булевых функций
с числом переменных 2n18. Громоздкость таблицы, неизбежная при увеличении местности
функций, компенсируется регулярностью и наглядностью таблиц. Изложение этого метода
можно найти в
ii
[2]. Симметричные таблицы позволяют:
-быстро и легко заполнять таблицу значениями минимизируемой функции благодаря
восьмеричной нумерации клеток;
-легко находить максимальные интервалы функции, благодаря свойству симметрии в структуре
таблицы;
-автоматизировать процесс минимизации, используя большую степень формализации
алгоритма склеивания клеток.
При использовании этого метода значения минимизируемой функции нумеруются
восьмеричными числами. Восьмеричный номер значения функции есть восьмеричное
12 13 9 8
14 15 11 10
6 7 3 2
4 5 1 0
4
Õ
1
Õ
3
Õ
4
(0-1- -0)
(01-011)
(-101-1)
(----10)
(----0-1)
(-0---1)
(----01-)
Х
2
представление его двоичного набора x
n
,...,x
1
.Двоичный набор разбивается справа налево на
группы по три разряда в каждой и каждая группа заменяется соответствующей восьмеричной
цифрой. При этом х
1
имеет минимальный двоичный вес, а x
n
- максимальный.
Базовой структурой при использовании этого метода является таблица для минимизации
функций, имеющих местность 2n6. Таблица, соответствующая максимальному числу
переменных, содержит 2
6
=64 клеток. Каждая клетка нумеруется двумя восьмеричными
цифрами, двоичный код этой последовательности при нумерации переменных справа налево(!)
определяет набор значений двоичных переменных функции шести переменных имеет вид
(x
6
x
5
x
4
x
3
x
2
x
1
). Для получения восьмеричного кода эта последовательность разбивается на
тройки справа налево и каждая тройка замещается соответствующей восьмеричной цифрой.
Восьмеричный код клетки обозначим (y
2
y
1
). В отмеченной симметричной таблице
указываются группы по 2
n-1
клетке, в которых указанная при отметке переменная принимает
единичные значения. Определение зон прямого и инверсного значений переменных
осуществляется следующим образом. Снизу всю горизонтальную строку клеток делят
вертикальной линией пополам. Полученные половины также делят вертикальными линиями
пополам. Далее полученные части снова делят пополам до тех пор, пока в каждой части слева
и справа от вертикальной линии не останется по одной клетке. Тогда для переменной х
1
первая
клетка слева представляет инверсное значение х
1
, следующие две клетки (удвоенное число)-
прямое значение х
1
, затем чередуются по две клетки прямое и инверсное значения х
1
до конца,
где будет одна клетка, которой приписывается инверсное значение х
1
. Для переменной х
2
инверсное значение, как и для остальных переменных, начинается слева, но для двух клеток,
следующее прямое значение - для четырех клеток (удвоенное число) и т.д. до конца. Затем для
переменной х
3
- области инверсного и прямого вхождений удвоенной длины по сравнению с
предшествующей переменной. Для трех старших переменных используется та же процедура
справа от таблицы в направлении сверху вниз.
Три младшие двоичные переменные указываются снизу таблицы с возрастанием индекса в
направлении сверху вниз, а три старшие переменные - справа от таблицы в направлении слева
направо в порядке возрастания индекса переменной. Пример симметричной таблицы для n=6
приведен на рис.9.Таким образом, каждая клетка таблицы имеет свой восьмеричный номер
(адрес) и в нее записывается значение функции из строки таблицы с тем же номером.
y
1
y
2
0 1 3 2 6 7 5 4
0
1 * * *
3 * * * * *
2 * * *
6 * *
7
5
4
Рис.9. Отмеченная симметричная таблица для минимизации булевых функций при n=6.
Стрелками указаны группы клеток с единичными значениями отмеченных переменных.
Склеивание единиц в таблице осуществляют следующим образом. Любая единица может
склеиваться по горизонтали: в группе из двух клеток с другой единицей или незаданным
набором, образуя интервал с одной свободной переменной; в группе из четырех клеток,
образуя интервал с двумя свободными переменными; в группе из 2
к
клеток, образуя интервалы
с к свободными переменными, где к2n. Аналогично можно склеивать и клетки по
вертикали. Склеиванию помогает визуальная симметрия возможных для склеивания клеток.
5
1
1
1
1
1
1
1
1
x
4
x
5
x
6
x
1
x
2
x
3
(0-1- -0)
(01-011)
(-101-1)
(----10)
(----0-1)
(-0---1)
(----01-)
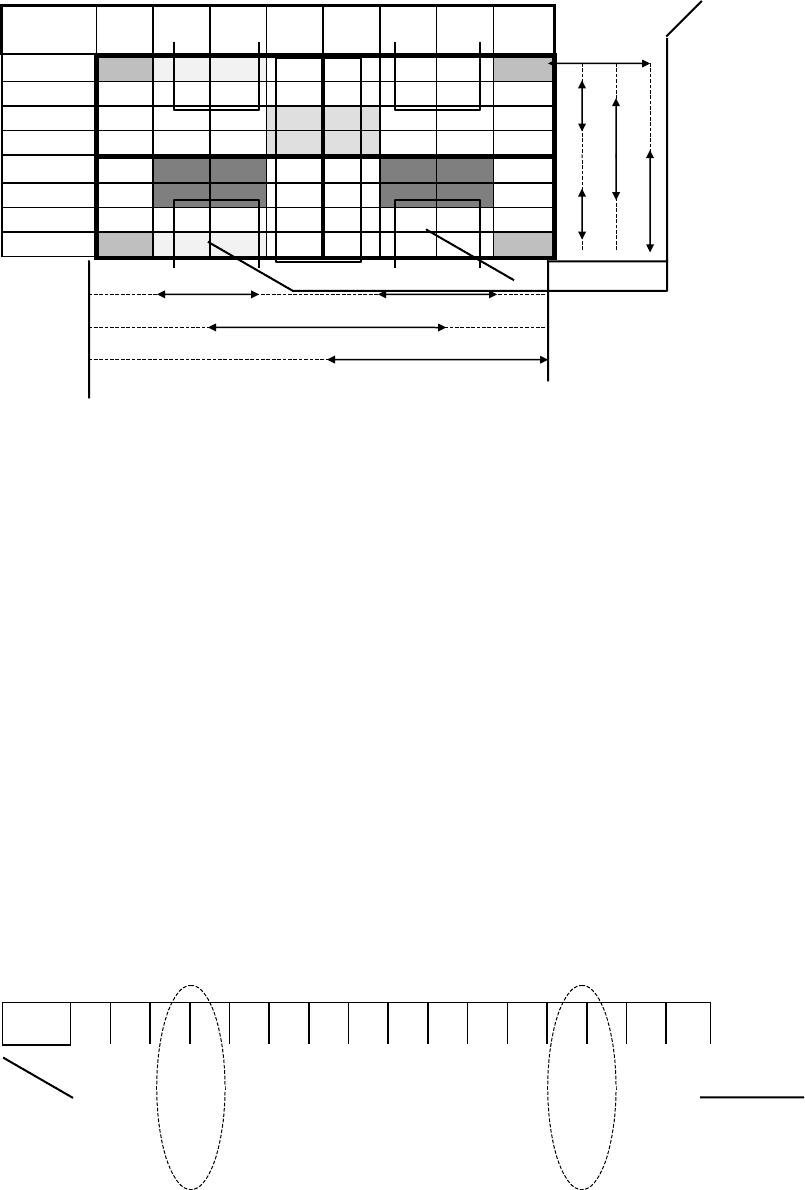
На рис.9 звездочками и подсветкой отмечены клетки, которые можно склеивать. Номер
клетки образуют две цифры-у
2
, соответствующая номеру строки таблицы, и у
1
,
соответствующая номеру столбца. Клетки с номерами 23 и 33 - интервал (01-011) с одной
свободной переменной х
4
. Клетки с номерами (25,27,65,67) - интервал (-101-1) с двумя
свободными переменными х
2
и х
6
. Клетки с номерами (10, 12, 14, 16, 30, 32,34,36) - интервал
(0-1--0) с тремя свободными переменными х
2
, х
3
, х
5
. Интервалы, соответствующие группам
склеиваемых клеток, отмечены сносками .
Основные оси симметрии таблицы выделены жирными линиями. Склеивание 2
к
клеток
возможно только при условии их симметричного расположения относительно основных или
дополнительных осей симметрии таблицы. Например, нельзя склеить четыре рядом
расположенные клетки с номерами 62, 65, 66, 67.
Пусть, например, 6-местная частично определенная функция задана следующим образом:
N
1
=(-000-1)(01--10), N
0
=(11---1) (-00-00). Соответствующая симметричная таблица и
процедура отыскания максимальных интервалов показаны на рис. 10.
y
1
y
2
0 1 3 2 6 7 5 4
0 0 1 1 * * * * 0
1 * * * * * * * *
3 * * * 1 1 * * *
2 * * * 1 1 * * *
6 * 0 0 * * 0 0 *
7 * 0 0 * * 0 0 *
5 * * * * * * * *
4 0 1 1 * * * * 0
Рис.10. Пример минимизации частично определенной 6-местной булевой функции.
Исходные интервалы функции помечены заливкой: единичные - более светлой, нулевые -
темнее. Для получения МДНФ склеивают клетки, в которых находятся 1 и *. Результаты
склеивания отмечены контурами и выносками. Для данной функции МДНФ=x
5
x
1
x
1
x
2
.
При увеличении местности функций таблица строится из базовой таблицы из 64 клеток. При
числе переменных 6n12 каждая часть из 2
6
клеток считается одной клеткой и нумеруется
той же последовательностью чисел-0,1,3,2,6,7,5,4 по горизонтали и по вертикали, но каждая
цифра в последовательности означает восьмеричную цифру третьего и четвертого разрядов
соответственно восьмеричного кода клетки.
Для 12 n 18 симметричная таблица строится аналогично предыдущей, но теперь базовой
клеткой является таблица из 2
12
клеток, а их нумерация той же последовательностью
восьмеричных цифр теперь соответствует пятому и шестому разрядам восьмеричного кода
клетки.
Прямые и инверсные вхождения переменных в таблице записывают тройками: младшие три
переменные записывают снизу, следующие три - справа, следующие три - снизу, следующие
три -справа, и так далее. Для обеспечения склеиваемости соседних клеток "больших" таблиц
нумерация в каждой следующей "большой " клетке должна быть зеркальной по отношению к
предыдущей.
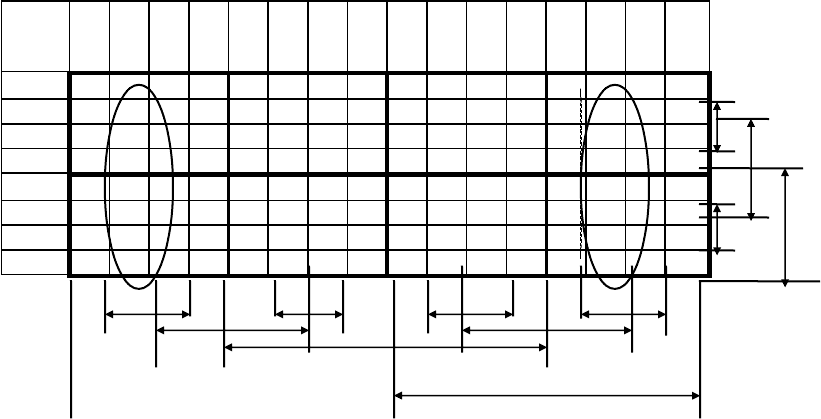
Составление карты для n=7 показано на рис. 11. Каждая клетка нумеруется тремя
восьмеричными цифрами, обозначаемыми (y
1
y
2
y
3
). В таблице обозначены основные оси
симметрии и два интервала, полученные в результате склеивания 1 и *. Им соответствует
МДНФ= x
2
x
3
x
1
x
3
.
y
3
0
6
x
4
x
5
x
6
1 1
1
1
1
1
1
1
x
4
x
5
x
6
x
1
x
2
x
3
(----10)
(----0-1)
(-0---1)
(----01-)
y
2
y
1
0 1 3 2 6 7 5 4 4 5
0 0 * * * * 0 * 0 * * * * * * * 0
1 0 * * * * 0 * * 0 * * * * * * *
3 0 * 1 1 * 0 0 * * 0 0 * 1 1 1 *
2 * * 1 1 * 0 0 * * 0 0 * 1 1 * 0
6 * 1 1 1 * * * 0 0 * 0 * 1 1 1 0
7 * 1 * * * * * 0 0 * * * * * * *
5 0 * * * * * * * * * * * * * * 0
4 0 * * * * * * * * * * * * * * 0
Рис.11. Симметричная таблица для n=7 и пример склеивания единичных и
неопределенных клеток для определения МДНФ.
Минимизация булевых функций большего числа переменных производится с использованием
изложенных принципов.
ЛИТЕРАТУРА
7
1
1 1
1
1 1
1
1
1
1
1
x
1
x
2
x
3
x
7
1
1
(----0-1)
(----01-)
i
А.Я. Савельев. Прикладная теория цифровых автоматов. М.: “Высшая школа”, 1987.
ii
С.П.Плеханов. Симметричные карты - мощное средство минимизации булевых функций при
проектировании цифровых устройств больших размерностей. “Электронная техника”. Сер.10.
Микроэлектронные устройства, вып. 4(88), 1991.
