Арзамасцев С.В. Полный факторный эксперимент
Подождите немного. Документ загружается.

Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ
Методические указания к выполнению лабораторных работ
по дисциплине «Моделирование и оптимизация
технологии полимерных материалов»
для студентов очной и заочной форм обучения специальности 240502.65
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2009
Дисциплина «Моделирование и оптимизация технологии
полимерных материалов» является завершающим этапом в
технологической подготовке инженеров химиков-технологов.
Лабораторные работы по дисциплине «Моделирование и
оптимизация технологии полимерных материалов» имеют следующие
цели:
ознакомление студентов с возможностями использования
средств вычислительной техники для решения задач моделирования,
оптимизации и управления производственными процессами в
технологии полимерных материалов;
привитие студентам навыков корректной постановки задач
технологии полимерных материалов для решения на ЭВМ, реализация
на них вычислительных алгоритмов и получение физически
обоснованных результатов расчета;
обучение студентов методологии проведения расчетных ис-
следований химических процессов на ЭВМ и использование последних
для решения задач проектирования и оптимизации химических
процессов.
В настоящих методических указаниях к выполнению лабораторных
работ по дисциплине «Моделирование и оптимизация технологии
полимерных материалов» рассматриваются вопросы практического
применения студентами приемов математического моделирования с
использованием методики полного факторного эксперимента, включая
следующие этапы:
- проверка воспроизводимости результатов эксперимента;
2
- построение математической модели в явном виде с расчетом
коэффициентов уравнения регрессии;
- проверка адекватности математической модели;
- инженерная интерпретация полученного уравнения регрессии,
позволяющая оценить зависимость параметра оптимизации от выбранных
факторов и сформулировать условия для повышения эффективности
изучаемого технологического процесса.
Теоретические подходы к моделированию
химико-технологических процессов.
Химико-технологические процессы представляют собой комплекс
взаимосвязанных и протекающих в сложной взаимозависимости явлений,
описание которых затрудняется необходимостью установления
закономерностей протекания элементарных процессов и их
взаимодействия и взаимовлияния друг на друга. Эти процессы относят к
классу стохастических, в котором изменение определяющих величин
происходит беспорядочно и часто дискретно. При этом значение выходной
величины не находится в однозначном соответствии с входной. Для
описания стохастических процессов используют статистико-
вероятностные методы.
Примером стохастического процесса может служить контактно-
каталитический процесс, в котором выход продукта изменяется с падением
активности катализатора, обусловленным его старением во времени.
Одним из методов, хорошо зарекомендовавшим себя в решении
такого рода задач, является метод полного факторного эксперимента, в
основе которого лежит способ построения зависимости влияния
3
определяющих факторов на параметр оптимизации в виде отрезка
степенного ряда Тейлора.
Метод полного факторного эксперимента включает в себя
последовательные этапы математического моделирования:
1. Выбор параметра (или параметров) оптимизации и влияющих
факторов.
2. Выбор основного уровня и интервала варьирования по каждому
фактору.
3. Проверка воспроизводимости результатов эксперимента.
4. Собственно построение математической модели с вычислением
коэффициентов уравнения регрессии.
5. Проверка адекватности уравнения регрессии.
6. Инженерная интерпретация уравнения регрессии.
Выбор параметра (или параметров) оптимизации, влияющих
факторов, а также выбор основного уровня и интервала варьирования по
каждому фактору подробно рассматриваются в лекционном курсе. На
лабораторных занятиях студенты приобретают навыки решения задач
проверки воспроизводимости результатов эксперимента, построения
математической модели и проверки её адекватности на ЭВМ.
Пример:
Изучить влияние на параметр оптимизации Y, в качестве которого
выбрана дуктильность (растяжимость) полимербитумного
композиционного материала при 0
0
С, следующих факторов:
1. Содержание каучука марки СКМС в составе
полимербитумного вяжущего (X
1
);
4
2. Количество вводимого в композицию полиэтилена высокого
давления (X
2
);
3. Время гомогенизации композиции (X
3
).
Для факторов 1-3 были выбраны основные уровни, интервалы
варьирования (табл. 1).
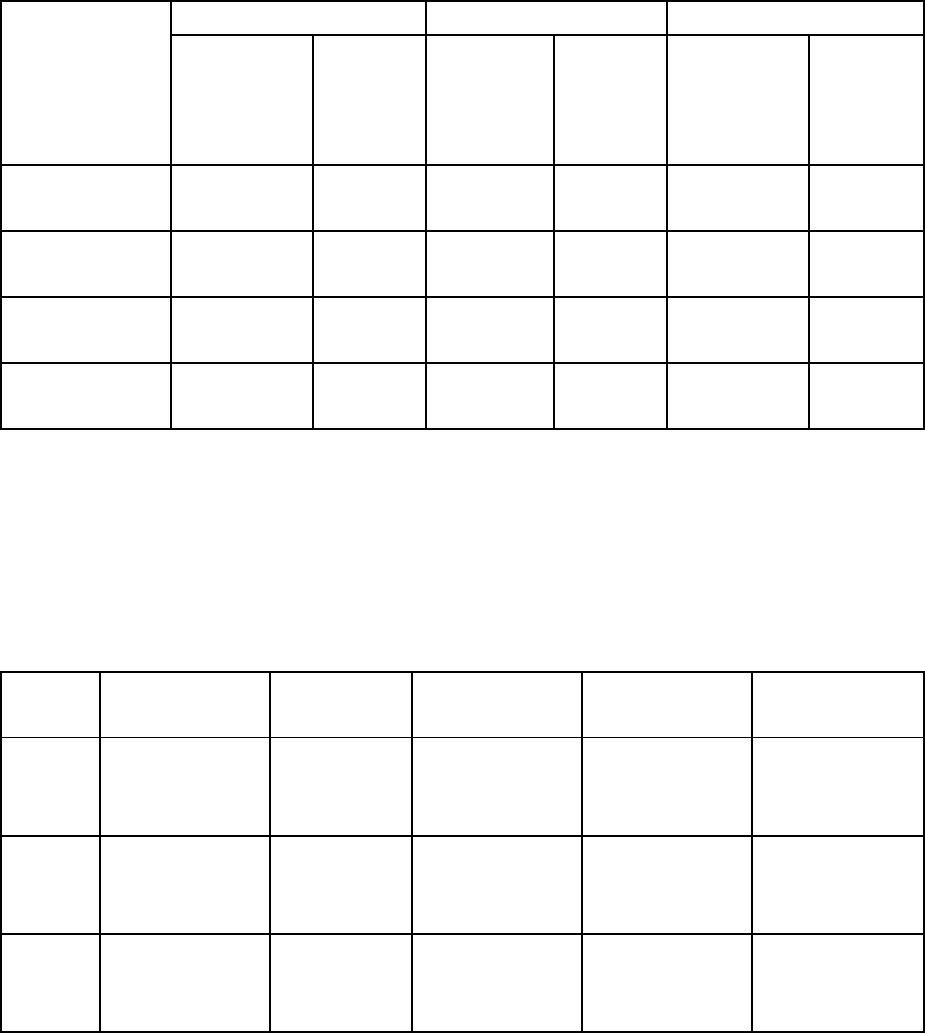
Таблица 1
Значения уровней факторов и интервалов варьирования
Показатель фактор X
1
фактор X
2
фактор X
3
натурально
е значение,
%
кодирова
нное
значение
натуральн
ое
значение,
%
кодирова
нное
значение
натурально
е значение,
мин
кодирова
нное
значение
Основной
уровень 1,0 0 0,3 0 40 0
Интервал
варьирования 0,5 0,2 20
Нижний
уровень 0,5 -1 0,1 -1 20 -1
Верхний
уровень 1,5 +1 0,5 +1 60 +1
Результаты эксперимента для проверки воспроизводимости опытов
представлены в табл. 2.
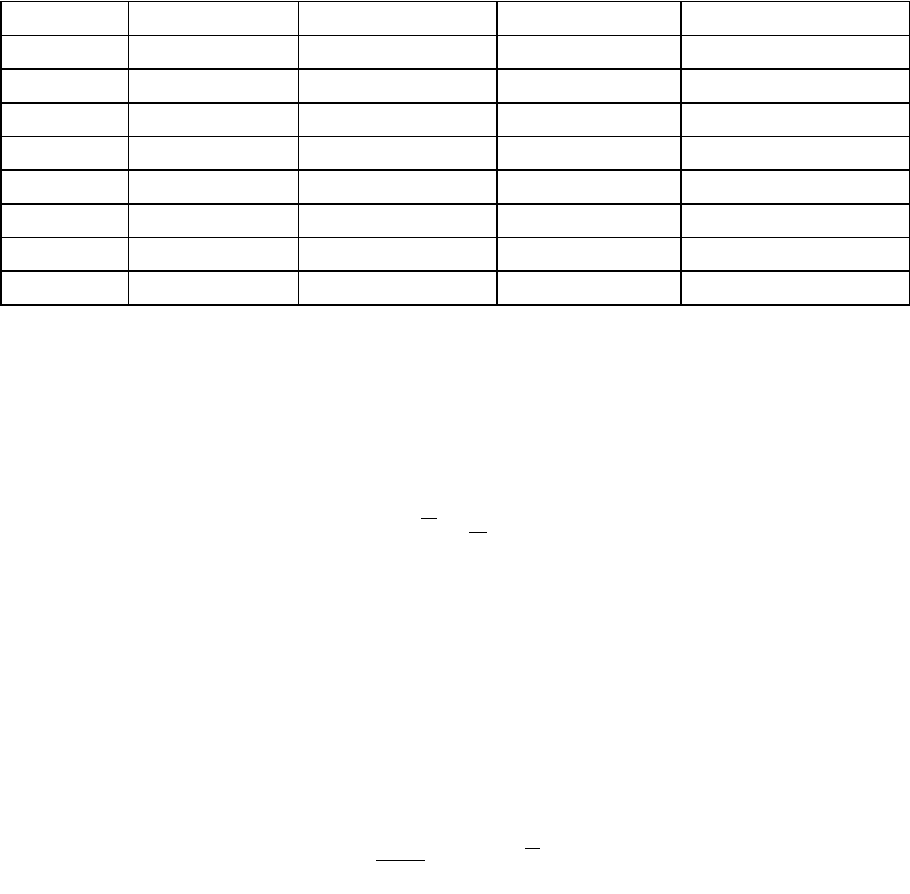
Таблица 2
Эксперимент для проверки воспроизводимости опытов
Серия № опыта фактор Х
1
факторХ
2
фактор Х
3
Значения Y
1
,
см
1 1
2
3
+1
+1
+1
+1
+1
+1
+1
+1
+1
7,1
10,1
8,1
2 1
2
3
-1
-1
-1
-1
-1
-1
-1
-1
-1
5,3
4,1
5,1
3 1
2
3
0
0
0
0
0
0
0
0
0
4,4
4,2
4,6
5
Матрица планирования полного факторного эксперимента
представлена в табл. 3.
Таблица 3
Матрица планирования полного факторного эксперимента
№ опыта X
1
X
2
X
3
Y
1эксп
, см
1 +1 +1 +1 8,5
2 +1 +1 -1 9,7
3 +1 -1 +1 6,3
4 +1 -1 -1 12,0
5 -1 +1 +1 3,5
6 -1 +1 -1 4,7
7 -1 -1 +1 3,6
8 -1 -1 -1 5,2
Выполнение задания:
Обработка результатов ведется по следующему алгоритму:
1. Для каждой серии параллельных опытов вычисляют среднее
арифметическое значение функции отклика по формуле
k
i
ijj
Y
k
Y
1
,
1
(1)
где j- номер серии параллельных опытов;
k-число параллельных опытов, проведенных при одинаковых условиях;
ij
Y
,
- текущее значение параметра оптимизации i-го опыта j-й серии.
2. Для каждой серии параллельных опытов вычисляется оценка дисперсии
2
j
s
по формуле:
2
,
2
)(
1
1
jijj
YY
k
s
(2)
6

3. Расчетное значение критерия Кохрена
Gp
находят из отношения
максимальной оценки дисперсии к сумме всех дисперсий
N
j
j
j
s
s
Gp
1
2
2
max
(3)
и сравнивают с табличным значением критерия Кохрена, выбираемым из
справочника при известных значениях общего количества дисперсий
N
, и
числом степеней свободы
f
, связанным с каждой из них как
1kf
. Если
выполняется условие
таблрасч
GG
, то опыты считаются воспроизводимыми,
а оценки дисперсий - однородными. Оценки однородных дисперсий можно
усреднить и найти величину, называемую оценкой дисперсии
воспроизводимости
N
j
jY
s
N
s
1
22
1
, (4)
с которой связано число степеней свободы
)1( kNf
. (5)
Оценку дисперсии среднего значения рассчитывают по формуле
k
s
s
Y
Y
2
2
. (6)
С ней также связано число степеней свободы
)1( kNf
. (7)
Результаты вычислений и выводы о воспроизводимости результатов
эксперимента по параметру оптимизации Y представлены в табл. 4.
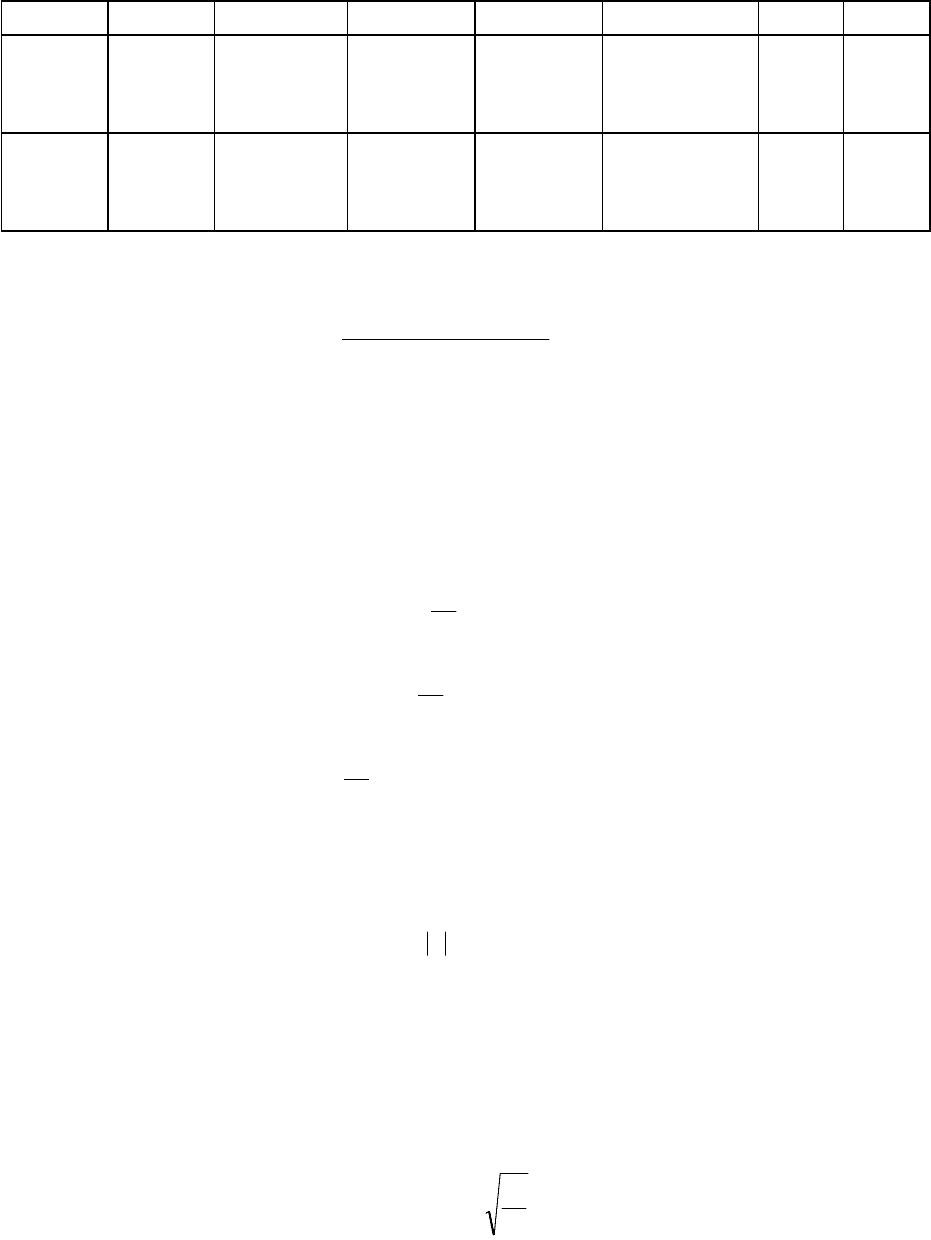
Таблица 4
Результаты проверки воспроизводимости эксперимента
по параметру оптимизации Y – дуктильности при 0
0
С
Серия №
опыта
фактор Х
1
фактор
Х
2
фактор
Х
3
Значения
Y
1
, см
Y
,
см
2
j
s
1 1
2
+1
+1
+1
+1
+1
+1
7,1
10,1 8,43 2,333
7
3 +1 +1 +1 8,1
2 1
2
3
-1
-1
-1
-1
-1
-1
-1
-1
-1
5,3
4,1
5,1
4,83 0,413
3 1
2
3
0
0
0
0
0
0
0
0
0
4,4
4,2
4,6
4,40 0,04
Расчетное значение критерия Кохрена
837,0
04,0413,0333,2
333,2
Gp
.
Табличное значение критерия Кохрена
табл
G
= 0,871
0,837<0,871 - опыты воспроизводимы.
Расчет коэффициентов уравнения регрессии ведется по формулам
(8)-(10) по исходным данным, представленным в табл. 3.
N
j
j
Y
N
b
1
0
1
; (8)
N
j
jjii
YX
N
b
1
1
; (9)
N
j
jjmjllm
YXX
N
b
1
1
, где
ml
. (10)
Оценка значимости коэффициентов уравнения регрессии проводится
по условию
tsb
b
, (11)
где b - коэффициент уравнения регрессии;
t - критерий Стьюдента;
s
b
- оценка коэффициента уравнения регрессии, определяемая по
формуле
N
s
s
Y
b
2
. (12)
Адекватность уравнения регрессии проверяется с помощью критерия
Фишера:
8

),min(
),max(
22
22
Yад
Yад
ss
ss
Fp
, (13)
где
2
ад
s
- оценка дисперсии адекватности. В числителе дроби (13)
находится большая, а в знаменателе - меньшая из указанных оценок
дисперсий.
Оценку дисперсии адекватности вычисляют по формуле
2
р2
1
j
э
jад
YY
BN
s
, (14)
где В - число коэффициентов регрессии искомого уравнения, включая
свободный член;
p
j
э
j
YY ,
- экспериментальное и расчетное значение функции отклика в j-том
опыте;
N - число опытов полного факторного эксперимента.
С дисперсией адекватности связано число степеней свободы
BNf
. (15)
Расчетное значение критерия Фишера выбирается из Приложения 1.
Уравнение регрессии считается адекватным, если выполняется условие
табл
FFp
. (16)
Расчеты по приведенному выше алгоритму проводят в Microsoft
Excel путем программирования ячеек электронной таблицы.
Пример расчета: Переносим данные таблицы 2 на лист созданной
книги Microsoft Excel (рис. 1).
Расчет
ср
Y
и
2
j
s
производим путем программирования
соответствующих ячеек книги Microsoft Excel. Ввод формулы в ячейку
всегда начинается со знака равенства. Для расчета
ср
Y
активизируем
(выделяем мышью) ячейку G3 книги. После этого при помощи клавиатуры
вводим знак равенства, а затем, используя мастер функций нажатием
правой кнопкой мыши на значок
x
f
, выбираем в категории
9
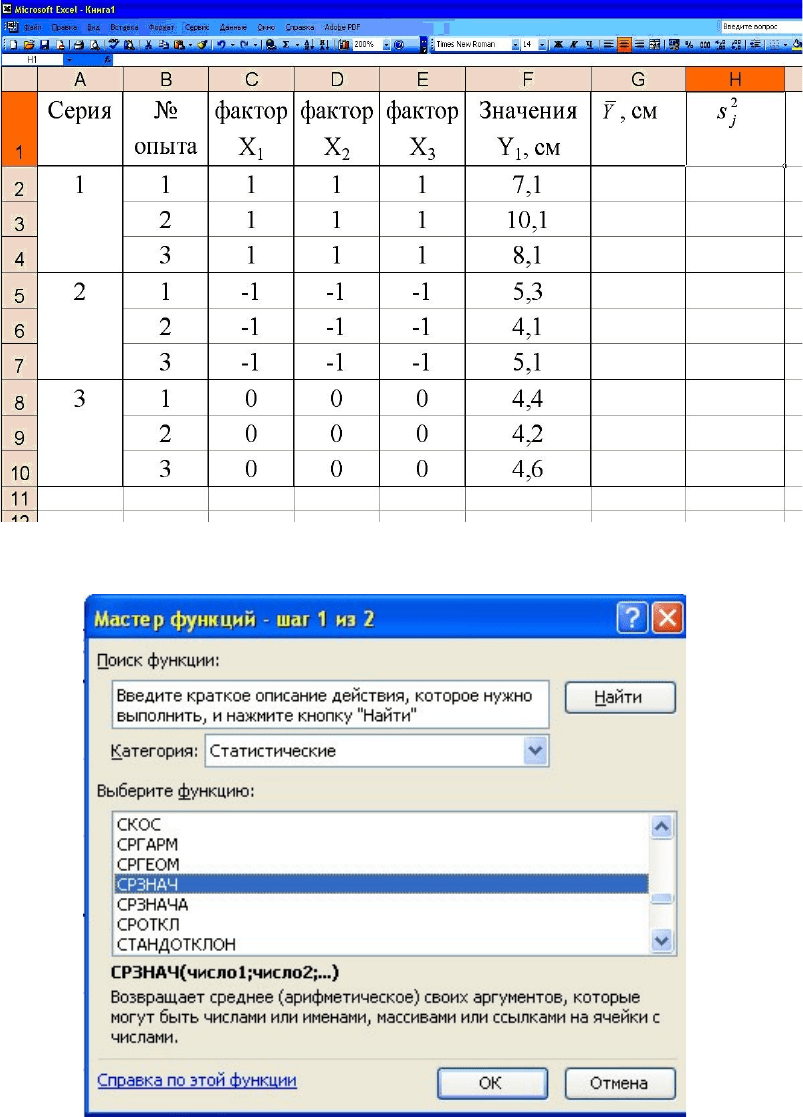
«Статистические» функцию «среднее значение» - СРЗНАЧ (рис. 2) и
нажимаем «ОК».
Рис. 1. Окно книги Microsoft Excel.
Рис. 2. Окно мастера функций.
10
