Арзамасцев С.В. Полный факторный эксперимент
Подождите немного. Документ загружается.

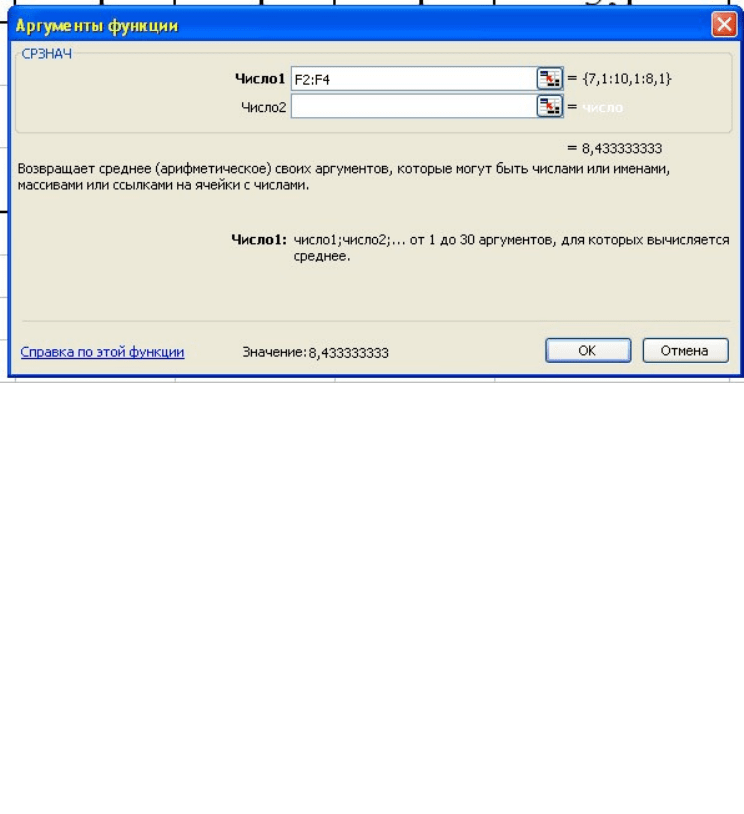
Рис. 2. Окно «Аргументы функции»
Для указания диапазона вычислений среднего значения указываем в
поле окна «число 1» (рис. 3) массив данных, находящихся в ячейках F2, F3
и F4, выделив правой кнопкой мыши ячейку F2 и, удерживая нажатой
клавишу «Shift», ячейку F4. Заканчивается ввод формулы нажатием
«Enter».
Для расчета оценки дисперсии для каждой серии параллельных
опытов
2
j
s
активизируем ячейку H3 и вводим в неё формулу (2)
следующим образом: =(1/2)*((F2-G3)^2+(F3-G3)^2+(F4-G3)^2).
Заканчивается ввод формулы нажатием «Enter».
Аналогичным образом для вычисления средних значений по
следующим сериям параллельных опытов программируем ячейки G6 и G9.
Для вычисления соответствующих оценок дисперсий второй и третьей
серий проведенных параллельных опытов ячейки H6 и H9. Результат
расчетов представлен на рис. 4.
11
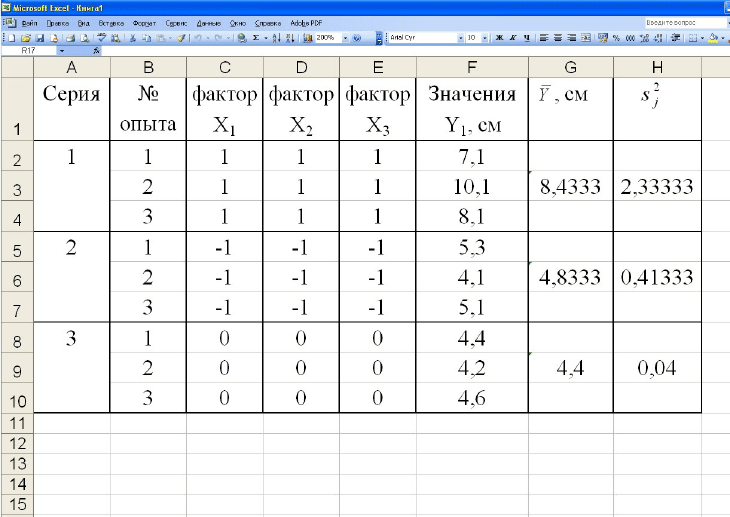
Рис. 4. Результат расчетов
Вводим в ячейку А12 текст «Расчетное значение критерия Кохрена»,
а в ячейку А13 - текст «Табличное значение критерия Кохрена». В ячейку
Е12 вводим формулу (3) как = МАКС(G3:G9)/СУММ(G3:G9), а в ячейку
Е13 – табличное значение критерия Кохрена из Приложения 1.
Для сравнения расчетного и табличного значений критерия Кохрена
используем логическую функцию «ЕСЛИ», программируя поле
«Лог_выражение» как F12<F13, поле «Значение_если_истина» как «опыты
воспроизводимы», а поле «Значение_если_ложь» как «опыты
невоспроизводимы» (рис. 5).
Далее по формулам (4) - (7) проводится расчет оценки дисперсии
воспроизводимости, оценки дисперсии среднего значения и связанных с
ними значений числа степеней свободы.
Итоговый вид расчета проверки воспроизводимости результатов
эксперимента представлен на рис. 6.
12
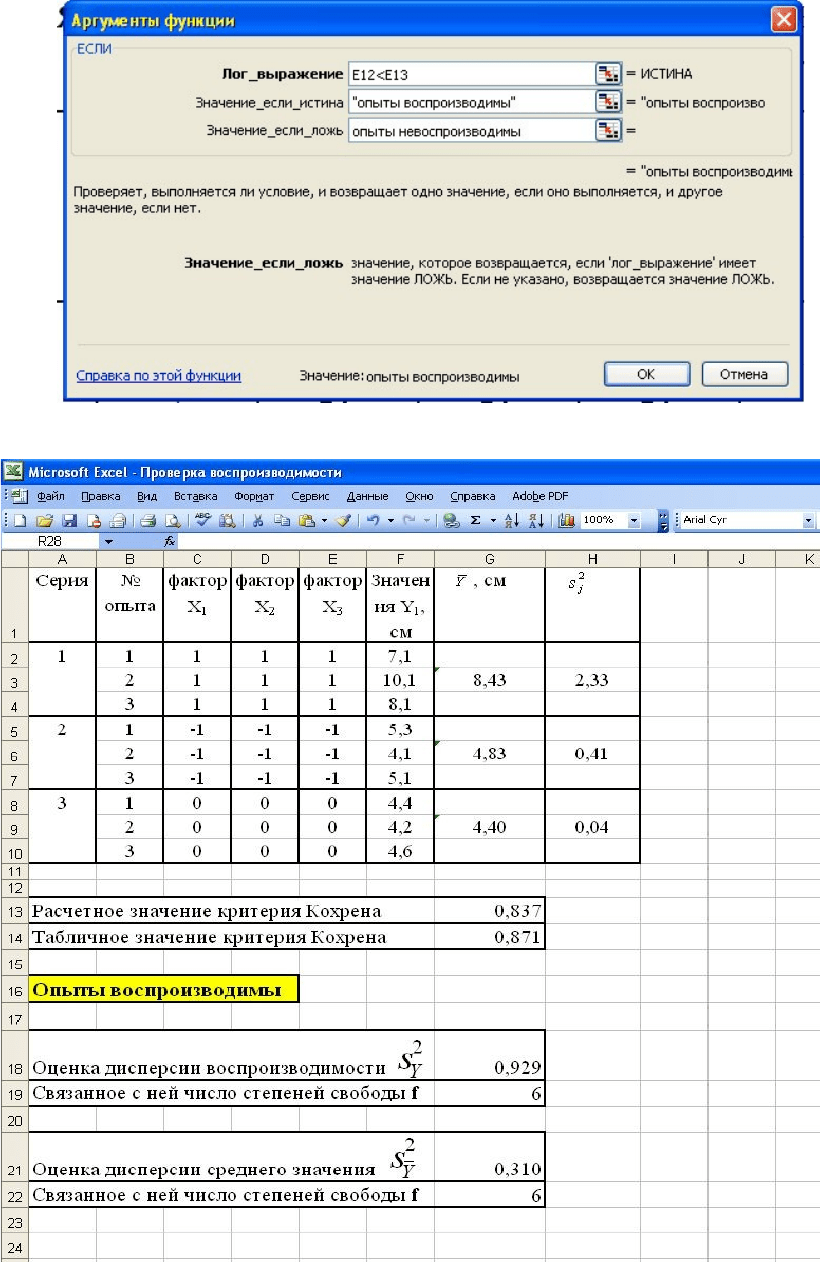
Рис. 5. Окно «Аргументы функции»
13
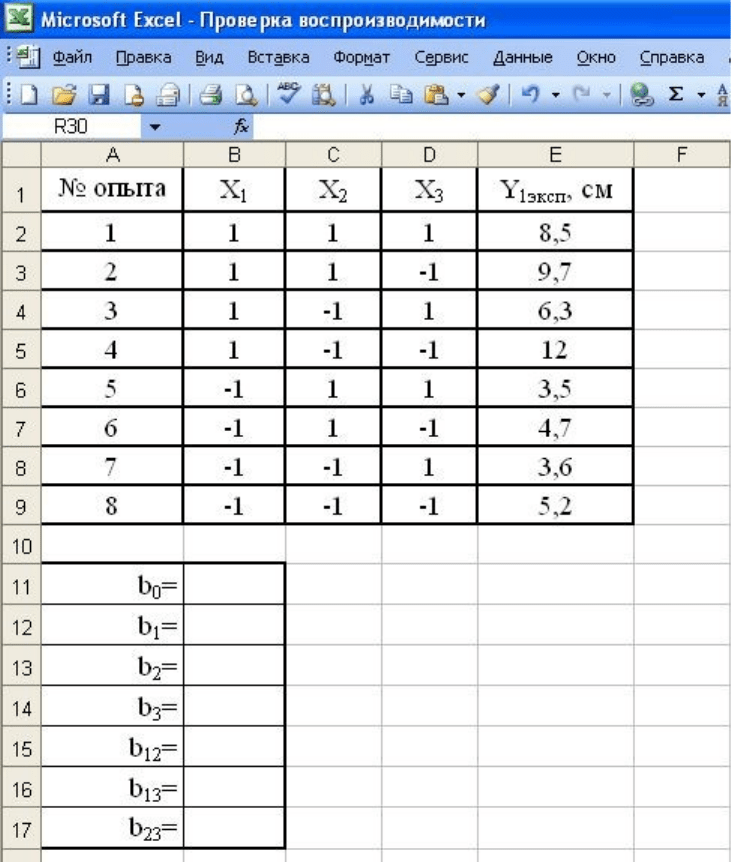
Рис. 6. Результаты расчета
Расчет коэффициентов уравнения регрессии проводится по
формулам (8) – (10).
Переносим данные таблицы 3 на лист 2 созданной книги Microsoft
Excel и создаем дополнительно таблицу для расчетов коэффициентов
уравнения регрессии (рис. 7).
Рис. 7. Расчет коэффициентов уравнения регрессии
В ячейку B11, используя мастер функций, вводим формулу, по
которой будет производиться расчет коэффициента b
0
(рис. 8).
14

Рис. 8. Расчет коэффициента уравнения регрессии b
0
Таким же образом, используя мастер функций, проводится
вычисление остальных коэффициентов уравнения регрессии.
Как показывает практика создания математической модели с
использованием метода полного факторного эксперимента, для точности
предсказания результатов и адекватности полученного уравнения
регрессии, можно не исключать из него элементы с незначимыми
коэффициентами уравнения регрессии. Поэтому проверку значимости
коэффициентов уравнении регрессии не проводят.
Полученное уравнение регрессии имеет вид:
3132213211
*5125,06125,00625,0212,10875,04375,26875,6 ХХXXXXXXXY
15
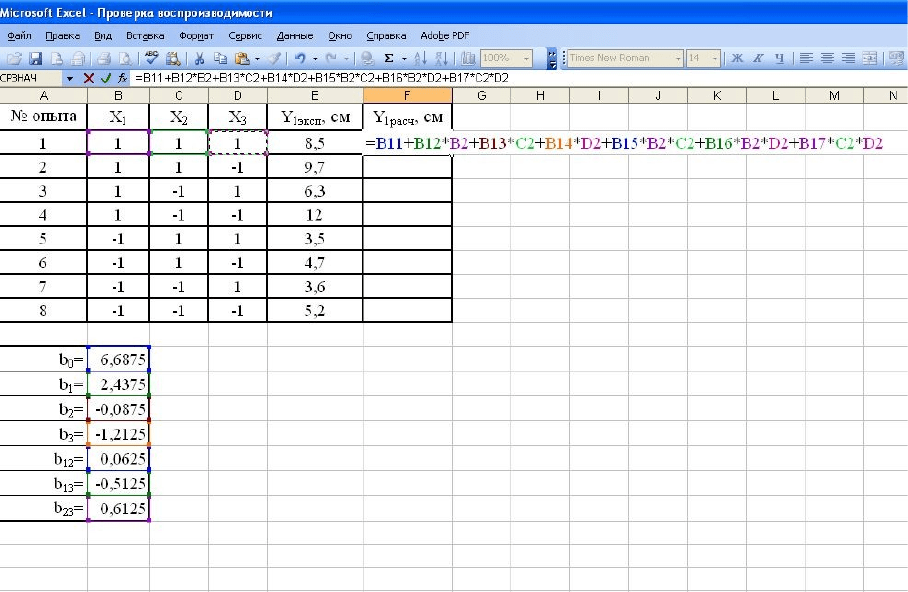
Проверка адекватности полученного уравнения проводятся
стандартным методом при помощи сравнения табличного и расчетного
значений критерия Фишера.
Решение этой задачи требует вычисления значений Y
1эксп
. Для этого в
уравнение регрессии построчно подставляются значения Х
1
-Х
3
из табл. 3,
соответствующие условиям проведения каждого из опытов полного
факторного эксперимента и методом программирования ячеек проводятся
соответствующие вычисления (рис. 9).
Рис. 9. Вычисление расчетных значений параметра оптимизации
Затем по формуле (14) рассчитывается значение дисперсии
адекватности, а по формуле (15) – связанное с ней число степеней
свободы.
Алгоритм расчета критерия Фишера заключается в сравнении
дисперсии воспроизводимости с дисперсией адекватности и делении
16
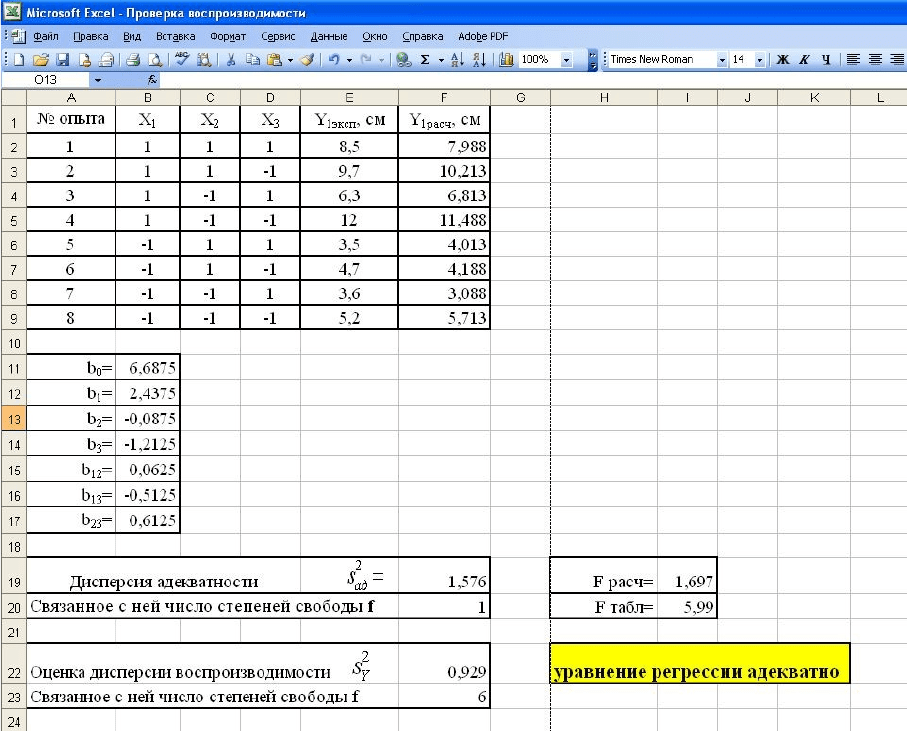
большего числа на меньшее. Программирование ячейки I19 заключается во
вводе в нее формулы =МАКС(F19;F22)/МИН(F19;F22). Табличное
значение критерия Фишера выбирается по Приложению 2 и вводится в
ячейку I20.
Для сравнения расчетного и табличного значений критерия Фишера
используем логическую функцию «ЕСЛИ», программируя поле
«Лог_выражение» как I19<I20, поле «Значение_если_истина» как
«уравнение регрессии адекватно», а поле «Значение_если_ложь» как
«уравнение регрессии неадекватно» (рис. 10).
Рис. 10. Результат проверки адекватности полученного уравнения регрессии
17
После положительного вывода об адекватности уравнения
регрессии, его подвергают инженерной интерпретации следующим
образом.
Известно, что величина коэффициента уравнения регрессии -
количественная мера его влияния. О характере влияния факторов говорят
знаки коэффициентов. Знак «плюс» свидетельствует о том, что с
увеличением значения фактора величина параметра оптимизации растет, а
при знаке «минус» - убывает. На основании полученного уравнения
регрессии можно сделать следующий вывод:
В исследованной области на дуктильность при 0
0
С наибольшее
влияние оказывает фактор X
1
- содержание в составе композиции каучука
СКМС, причем с увеличением его количества значение параметра
оптимизации будет возрастать. Меньшее влияние оказывает время
гомогенизации композиции; характер этого влияния отрицателен, т.е. с
увеличением времени гомогенизации дуктильность снижается.
Содержание полиэтилена высокого давления оказывает незначительное
влияние на дуктильность при 0
0
С.
Результаты расчета записываются в виде файла, а выполненная
лабораторная работа соответствующим образом оформляется и сдается на
проверку преподавателю.
ЛИТЕРАТУРА
1. Саутин С.Н. Планирование эксперимента в химии и химической
технологии. / С.Н. Саутин. - Л.: Химия, 1975. – 48 с.
2. Адлер Ю.П. Введение в планирование эксперимента./ Ю.П. Адлер. - М.:
Металлургия, 1969. – 157 с.
3. Адлер Ю.П. Планирование эксперимента при поиске оптимальных
условий./ Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. - М.:Наука, 1971.-
297 с.
18

4. Кафаров В.В. Методы кибернетики в химии и химической технологии./
В.В. Кафаров. -М.: Химия, 1985. – 448 с.
5. Закгейм А.Ю. Общая химическая технология: Введение в
моделирование химико-технологических процессов./ А.Ю. Закгейм. - М.:
Логос, 2009. – 304 с.
6. Кузичкин Н.В. Методы и средства автоматизированного расчета
химико-технологических систем./ Н.В. Кузичкин, С.Н. Саутин, А.Е.
Пунин. - Л: Химия, 1987. – 152 с.
7. Леонтьев В.П. Новейшая энциклопедия персонального компьютера
2009./В.П. Леонтьев. – М.: ОЛМА Медиа Групп, 2009. – 928 с.
8. Ефимова О.П. Курс компьютерной технологии./ О.П. Ефимова, В.Н.
Морозов, Н.П. Угринович. – М.: Издательство АСТ; ABF, 2005. – 432 с.
9. Кольцова Э.М. Методы синергетики в химии и химической технологии:
Учебное пособие для вузов./ Э.М. Кольцова, Л.С. Гордеев. – М.: Химия,
1999. – 256 с.
10. Бояринов А.И. Методы оптимизации в химической технологии./ А.И.
Бояринов, В.В. Кафаров. - М.: Химия, 1973. – 564 с.
11. Бондарь А. Г. Планирование эксперимента в химической технологии
(основные положения, примеры и задачи)./ А.Г. Бондарь, Г.А. Статюха. -
Киев: Высшая школа. 1976г. - 184 с.
12. Дорохов И.Н. Системный анализ процессов химической технологии./
И.Н. Дорохов, В.В. Кафаров. - М.: Наука, 1989. – 376 с.
Приложение 1.
Значение критерия Кохрена
N
f=k-1
1 2 3 4 5 6 7 8
2 0,999 0,975 0,939 0,906 0,877 0,853 0,833 0,816
3 0,967 0,781 0,798 0,746 0,707 0,677 0,653 0,633
4 0,907 0,768 0,684 0,629 0,590 0,560 0,637 0,518
5 0,841 0,684 0,598 0,544 0,507 0,478 0,456 0,439
19

6 0,781 0,616 0,532 0,480 0,445 0,418 0,398 0,382
7 0,727 0,561 0,480 0,431 0,397 0,373 0,354 0,338
8 0,680 0,516 0,438 0,391 0,360 0,336 0,319 0,304
9 0,639 0,478 0,403 0,358 0,329 0,307 0,290 0,277
10 0,602 0,445 0,373 0,331 0,303 0,282 0,267 0,254
Приложение 2.
Значение критерия Фишера
Число
степене
й
свобод
ы f
2
Число степеней свободы f
1
(для числителя)
1 2 3 4 5 6 7 8
1 161,45 199,50 215,71 224,58 230,16 23,99 236,77 238,88
2 18,51 19,00 19,16 19,25 19,30 19,33 19,35 19,37
3 10,13 9,55 9,28 9,12 9,01 8,94 8,89 8,85
4 7,71 6,94 6,59 6,39 6,26 6,16 6,09 6,04
5 6,61 5,79 5,41 5,19 5,05 4,95 4,88 4,82
6 5,99 5,14 4,73 4,53 4,39 4,28 4,21 4,15
7 5,59 4,74 4,35 4,12 3,97 3,87 3,79 3,73
8 5,32 4,46 4,07 3,84 3,69 3,58 3,50 3,44
9 5,12 4,26 3,86 3,63 3,48 3,37 3,29 3,24
10 4,97 4,10 3,71 3,48 3,33 3,22 3,14 3,07
11 4,84 3,98 3,59 3,36 3,20 3,10 3,01 2,95
12 4,75 3,89 3,49 3,26 3,11 3,00 2,91 2,85
13 4,67 3,81 3,41 3,18 3,03 2,92 2,83 2,77
14 4,60 3,74 3,34 3,11 2,96 2,85 2,76 2,70
15 4,54 3,68 3,29 3,06 2,90 2,79 2,71 2,64
16 4,49 3,63 3,24 3,01 2,85 2,74 2,66 2,59
17 4,45 3,59 3,20 2,97 2,81 2,70 2,71 2,55
18 4,41 3,56 3,16 2,93 2,77 2,66 2,58 2,51
19 4,38 3,52 3,13 2,90 2,74 2,63 2,54 2,48
20 4,35 3,49 3,10 2,87 2,71 2,60 2,51 2,45
ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ
Методические указания к выполнению лабораторных работ
по дисциплине «Моделирование и оптимизация
технологии полимерных материалов»
Составил: Арзамасцев Сергей Владимирович.
20
