Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

138 Chapter 2

Fourier coefﬁcients

> F(n):=Int(f(x)*phi[m,n](x)*w(x),x=0..b);F(n):=‘F(n)’:

F(n) :=



f(x)BesselJ



m, λ

m,n











BesselJ



m, λ

m,n



x dx

dx (2.277)

This is the Fourier-Bessel series expansion of f(x) in terms of the “complete” set of

eigenfunctions for the particular Sturm-Liouville operator and boundary conditions over the

interval. Here, J(m, λx) denotes the Bessel function of the ﬁrst kind of order m.

DEMONSTRATION: Develop the Fourier-Bessel series expansion for f(x) = x over the

interval I ={x |0 <x<1} in terms of the Bessel functions of the ﬁrst kind of order m = 1. We

assign the system values

> a:=0;b:=1;m:=1;f(x):=x;

a := 0

b := 1

m := 1

f(x) := x (2.278)

SOLUTION: Evaluation of the eigenvalues from the roots of the eigenvalue equation yields

> BesselJ(m,lambda[m,n]*b)=0;

BesselJ



1,λ

1,n



= 0 (2.279)

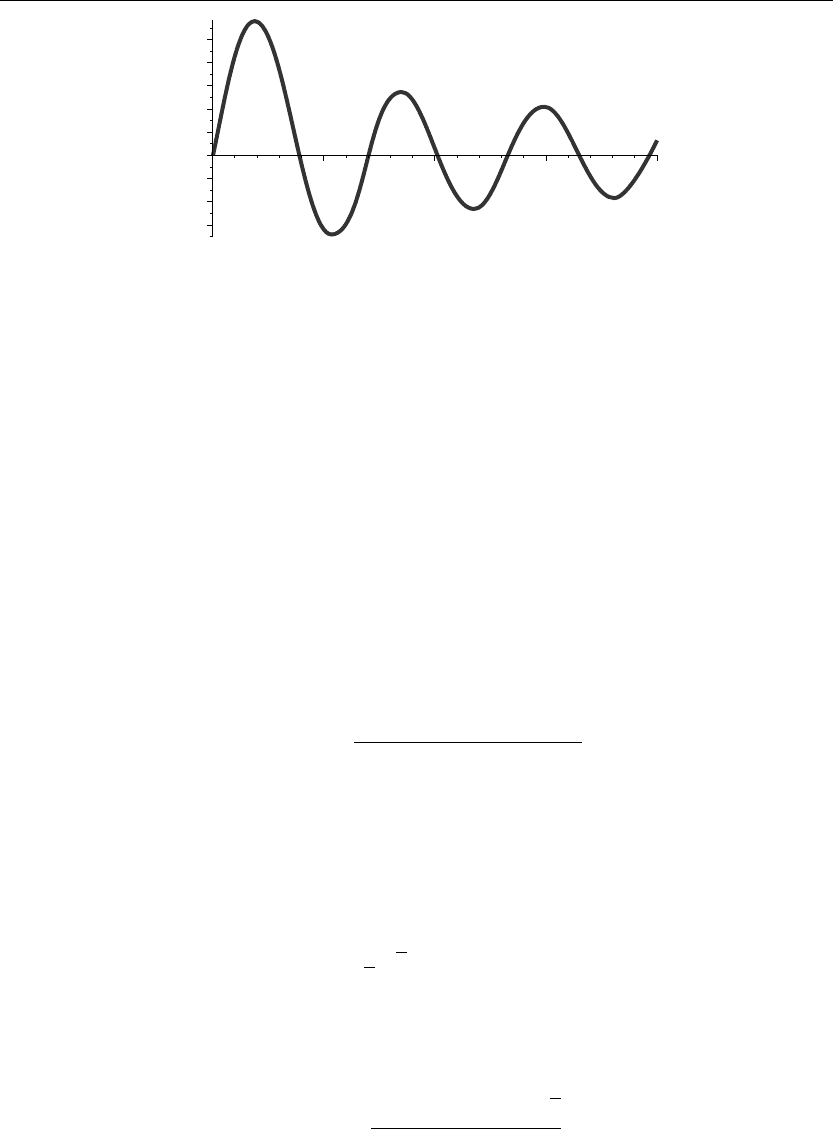
> plot(BesselJ(m,v),v=0..20,thickness=10);

If we set v = λb, then the eigenvalues are found from the intersection points of the curve with

the v-axis shown in Figure 2.18. We evaluate a few of these eigenvalues from the Maple fsolve

command for the roots of the eigenvalue equation to be given as

> lambda[1,1]:=(1/b)*fsolve(BesselJ(m,v)=0,v=1..4);

1,1

:= 3.831705970 (2.280)

> lambda[1,2]:=(1/b)*fsolve(BesselJ(m,v)=0,v=4..9);

1,2

:= 7.015586670 (2.281)

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 139

5101520

20.3

20.2

20.1

0.1

0.2

0.3

0.4

0.5

Figure 2.18

> lambda[1,3]:=(1/b)*fsolve(BesselJ(m,v)=0,v=9..12);

1,3

:= 10.17346814 (2.282)

> lambda[1,4]:=(1/b)*fsolve(BesselJ(m,v)=0,v=12..16);

1,4

:= 13.32369194 (2.283)

> lambda[1,5]:=(1/b)*fsolve(BesselJ(m,v)=0,v,16..19);

1,5

:= 16.47063005 (2.284)

Normalization

> norm:=sqrt(Int(w(x)*(BesselJ(m,lambda[m,n]*x))ˆ2,x=0..b));

norm :=









xBesselJ



1,λ

1,n



dx (2.285)

Substitution of the eigenvalue equation simpliﬁes the norm

> norm:=radsimp(subs(BesselJ(1,lambda[1,n])=0,value(%)));

norm :=

√

2BesselJ



0,λ

1,n



(2.286)

Orthonormal eigenfunctions

> phi[m,n](x):=BesselJ(m,lambda[m,n]*x)/norm;

1,n

(x) :=

BesselJ



1,λ

1,n



√

BesselJ



0,λ

1,n



(2.287)

140 Chapter 2

Fourier coefﬁcients

> F(n):=Int(f(x)*phi[m,n](x)*w(x),x=a..b);

F(n) :=



BesselJ



1,λ

1,n



√

BesselJ



0,λ

1,n



dx (2.288)

Substitution of the eigenvalue equation simpliﬁes the preceding equation

> F(n):=subs(BesselJ(1,lambda[1,n])=0,value(%));

F(n) := −

√

1,n

(2.289)

> Series:=Sum(F(n)*phi[m,n](x),n=1..inﬁnity);

Series :=

∞



n=1



−

2BesselJ



1,λ

1,n



1,n

BesselJ



0,λ

1,n





(2.290)

First ﬁve terms in expansion

> Series:=sum(F(n)*phi[m,n](x),n=1..5):

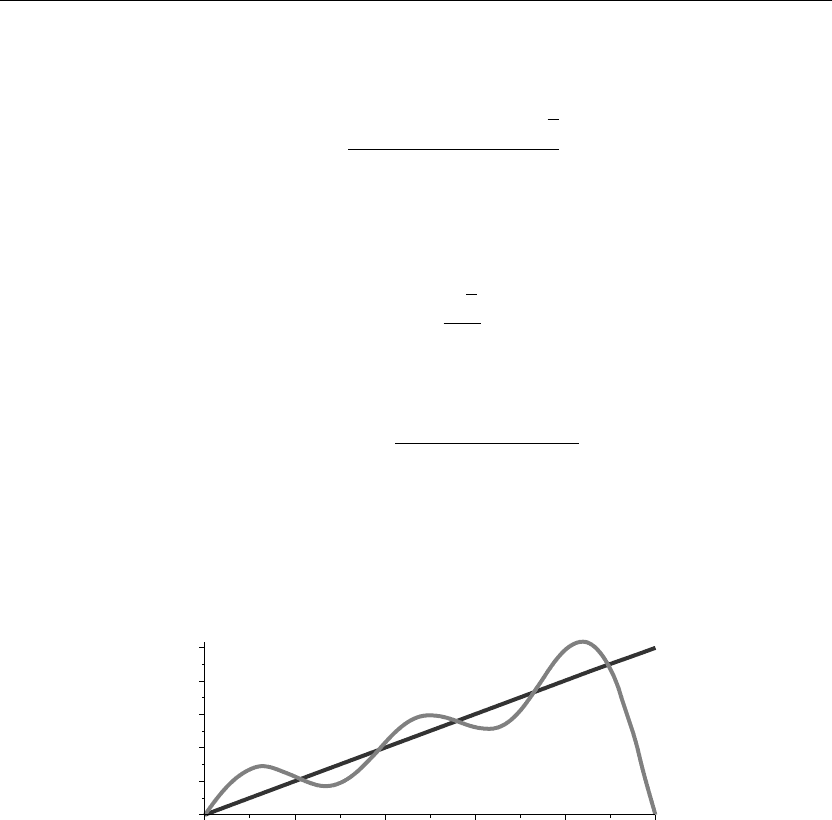
> plot({Series,f(x)},x=a..b,thickness=10);

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 2.19

The two curves in Figure 2.19 depict the function f(x) and its series expansion approximation

in terms of the Bessel functions of the ﬁrst kind of order m = 1, which satisfy the given

boundary conditions over the interval. Note that f(x) satisﬁes the given boundary conditions at

the left but fails to do so at the right end point.

EXAMPLE 2.6.3: Consider the Bessel operator with Neumann conditions. We seek the

eigenvalues and corresponding orthonormal eigenfunctions for the Bessel differential equation

of order m = 0 [Sturm-Liouville type for p(x) = x, q(x) = 0, w(x) = x] over the interval

I ={x |0 <x<b}. The boundary conditions are that the solution be ﬁnite at the origin and that

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 141

there is a type 2 condition at the point x = b. The Sturm-Liouville problem involving the

Bessel operator is nonregular over this interval. From Green’s formula in Section 2.2, since

p(0) = 0, we continue to obtain a condition for orthogonality over this interval if, in addition to

requiring the solution to be ﬁnite at the origin, we further require that at x = b, its ﬁrst

derivative vanishes (see Exercise 2.34).

Bessel differential equation of order m = 0



y(x)





y(x)



+λ

y(x) = 0

Boundary conditions

y(0)

< ∞ and y

(b) = 0

SOLUTION: We consider two possibilities for values of λ. We ﬁrst consider the case for

λ = 0. The system basis vectors are

> restart:y1(x):=1;y2(x):=ln(x);

y1(x) := 1

y2(x) := ln(x) (2.291)

General solution

> y(x):=C1*y1(x)+C2*y2(x);

y(x) := C1 +C2 ln(x) (2.292)

Since ln(x) fails to exist at x = 0, we set C2 = 0, giving

> y(x):=C1;

y(x) := C1 (2.293)

Substituting into the boundary condition at the periphery yields

> eval(subs(x=a,diff(y(x),x)))=0;

0 = 0 (2.294)

Thus, C1 is arbitrary and the eigenvalue and eigenfunction corresponding to λ = 0 are given as

> lambda[0]:=0;

:= 0 (2.295)

> phi[0](x):=1;

(x) := 1 (2.296)

142 Chapter 2

We next consider the case for λ>0. The system basis vectors are

> y1(x):=BesselJ(0,lambda*x);y2(x):=BessselY(0,lambda*x);

y1(x) := BesselJ(0, λx)

y2(x) := BesselY(0, λx) (2.297)

General solution

> y(x):=C1*y1(x)+C2*y2(x);

y(x) := C1 BesselJ(0, λx) +C2 BesselY(0, λx) (2.298)

Substituting the boundary condition at the origin indicates that, since the Bessel function of the

second kind [Y(m, μx)] is not ﬁnite at the origin, we must set C2 = 0. Substituting the

remaining condition at x = b yields

> eval(subs({x=b,C2=0},diff(y(x),x)))=0;

−C1 BesselJ(1, λ b)λ = 0 (2.299)

The only nontrivial solutions to the above occur when C1 is arbitrary and λ satisﬁes the

following eigenvalue equation

BesselJ

(

1,λ

)

= 0 (2.300)

for n = 1, 2, 3,....

Nonnormalized eigenfunctions are

> phi[n](x):=BesselJ(0,lambda[n]*x);

(x) := BesselJ

(

0,λ

)

(2.301)

Normalization

Evaluating the norm from the inner product of the eigenfunctions, with respect to the weight

function w(x) = x over the interval, yields, for n = 0,

> w(x):=x:norm0:=sqrt(Int(phi[0](x)ˆ2*w(x),x=0..b));

norm0 :=









x dx (2.302)

> norm0:=radsimp(value(%));

norm0 :=

√

2b (2.303)

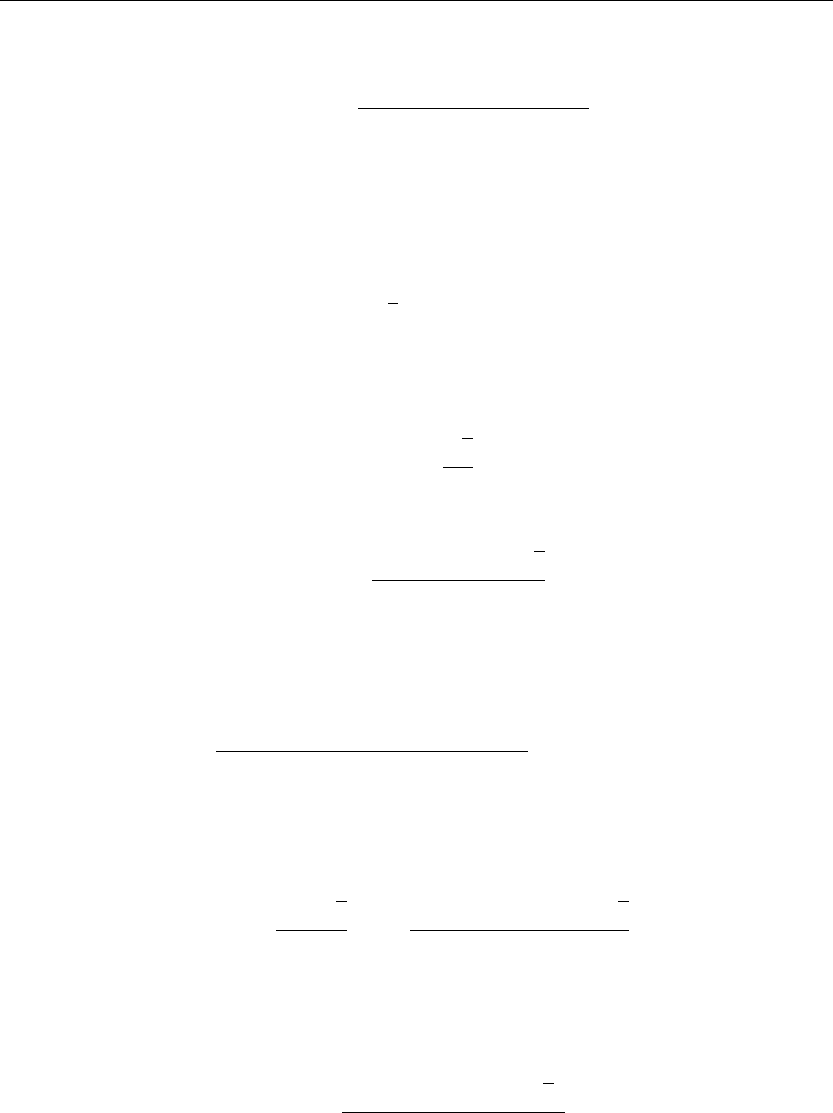
Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 143

For n = 1, 2, 3,...,

> norm1:=sqrt(Int(phi[n](x)ˆ2*w(x),x=0..b));norm1:=value(%):

norm1 :=









(

BesselJ

(

0,λ

))

x dx (2.304)

Substitution of the eigenvalue equation simpliﬁes the norm

> norm1:=radsimp(subs(BesselJ(1,lambda[n]*b)=0,norm1));

norm1 :=

√

2 b BesselJ

(

0,λ

)

(2.305)

Orthonormal eigenfunctions

> phi[0](x):=phi[0](x)/norm0;

(x) :=

√

(2.306)

> phi[n](x):=phi[n](x)/norm1;phi[p](x):=subs(n=p,phi[n](x)):

(x) :=

BesselJ

(

0,λ

)

√

bBesselJ

(

0,λ

)

(2.307)

Statement of orthonormality

> Int(phi[n](x)*phi[p](x)*w(x),x=0..b)=delta(n,p);



2BesselJ

(

0,λ

)

BesselJ



0,λ



BesselJ

(

0,λ

)

BesselJ



0,λ



dx = δ(n, p) (2.308)

Generalized Fourier series expansion

> f(x):=F(0)*phi[0](x)+Sum(F(n)*phi[n](x),n=1..inﬁnity);f(x):=‘f(x)’:

f(x) :=

F(0)

√

∞



n=1

F(n) BesselJ

(

0,λ

)

√

bBesselJ

(

0,λ

)

(2.309)

Fourier coefﬁcients

> F(n):=Int(f(x)*phi[n](x)*w(x),x=0..b);F(n):=‘F(n)’:

F(n) :=



f(x)BesselJ

(

0,λ

)

√

bBesselJ

(

0,λ

)

dx (2.310)

144 Chapter 2

> F(0):=Int(f(x)*phi[0](x)*w(x),x=0..b);F(0):=‘F(0)’:

F(0) :=



f(x)

√

dx (2.311)

This is the Fourier-Bessel series expansion of f(x) in terms of the “complete” set of

orthonormal eigenfunctions for the particular Sturm-Liouville operator and boundary

conditions over the interval.

DEMONSTRATION: Develop the Fourier-Bessel series expansion for f(x) = 1 −x

over the

interval I ={x |0 <x<1} in terms of the preceding eigenfunctions. We assign the system

values

> a:=0;b:=1;f(x):=1−xˆ2;

a := 0

b := 1

f(x) := 1 −x

(2.312)

SOLUTION: Evaluation of the eigenvalues from the roots of the eigenvalue equation yields

> BesselJ(1,lambda[n]*b)=0;

BesselJ

(

1,λ

)

= 0 (2.313)

> plot(BesselJ(1,v),v=0..20,thickness=10);

If we set v = λb, then the eigenvalues are found from the intersection points of the curve with

the v-axis shown in Figure 2.20. We evaluate a few of these eigenvalues from the Maple fsolve

command for the roots of the eigenvalue equation to be given as

5101520

20.3

20.2

20.1

0.1

0.2

0.3

0.4

0.5

Figure 2.20

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 145

> lambda[1]:=(1/b)*fsolve(BesselJ(1,v)=0,v=1..4);

:= 3.831705970 (2.314)

> lambda[2]:=(1/b)*fsolve(BesselJ(1,v)=0,v=4..9);

:= 7.015586670 (2.315)

> lambda[3]:=(1/b)*fsolve(BesselJ(1,v)=0,v=9..12);

:= 10.17346814 (2.316)

> lambda[4]:=(1/b)*fsolve(BesselJ(1,v)=0,v=12..16);

:= 13.32369194 (2.317)

> lambda[5]:=(1/b)*fsolve(BesselJ(1,v)=0,v=16..19);

:= 16.47063005 (2.318)

Fourier coefﬁcients

> F(n):=eval(Int(f(x)*phi[n](x)*w(x),x=a..b));

F(n) :=





1 −x



BesselJ

(

0,λ

)

√

BesselJ

(

0,λ

)

dx (2.319)

Substitution of the eigenvalue equation simpliﬁes the preceding equation

> F(n):=subs(BesselJ(1,lambda[n]*b)=0,value(%));

F(n) := −

√

(2.320)

> F(0):=eval(Int(f(x)*phi[0](x)*w(x),x=a..b));

F(0) :=





1 −x



√

2x dx (2.321)

> F(0):=value(%);

F(0) :=

√

2 (2.322)

> Series:=eval(F(0)*phi[0](x)+Sum(F(n)*phi[n](x),n=1..inﬁnity));

Series :=

∞



n=1



−

4BesselJ

(

0,λ

)

BesselJ

(

0,λ

)



(2.323)

146 Chapter 2

First ﬁve terms in the expansion

> Series:=F(0)*phi[0](x)+sum(F(n)*phi[n](x),n=1..5):

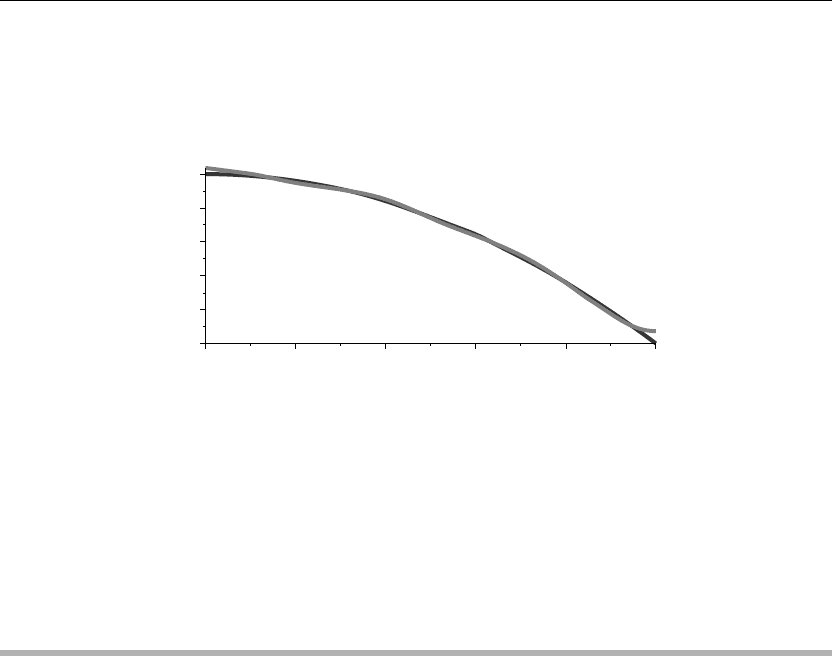
> plot({Series,f(x)},x=a..b,thickness=10);

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 2.21

The two curves in Figure 2.21 depict the function f(x) and its Fourier series expansion

approximation in terms of the Bessel functions of the ﬁrst kind of order zero, which satisfy the

given boundary conditions. Note that f(x) satisﬁes the given boundary condition at the left but

fails to do so at the right end point.

Chapter Summary

Sturm-Liouville operator acting on y(x)

L(y) = D(p(x)D(y)) +q(x)y

The Sturm-Liouville differential equation

L(ϕ) +λ w(x)ϕ = 0

Regular homogeneous boundary conditions

ϕ(a) +κ

(a) = 0

and

ϕ(b) +κ

(b) = 0

Generalized Fourier series expansion

f(x) =

∞



n=0

F(n)ϕ

(x)

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 147

Statement of orthonormality with respect to the weight function w(x)



(x) φ

(x) w(x) dx = δ(n, m)

Generalized Fourier coefﬁcients

F(n) =



f(x) φ

(x) w(x) dx

The generalized Fourier series expansions above are based on the orthonormalized

eigenfunction solutions to Sturm-Liouville boundary value problems. These generalized series

expansions will play an important role in the solutions to boundary value problems in partial

differential equations.

Exercises

2.1. From Section 2.2, any second-order linear differential equation of the form

(x)



y(x)



(x)



y(x)



(x)y(x) = 0

can be converted into self-adjoint form by multiplying by the integrating factor

r(x) =



(x)

Consider the following differential equations shown below. In all cases, evaluate the

integrating factor, identify p(x), q(x), and the weight function w(x), and rewrite the

equations in the Sturm-Liouville (self-adjoint) form

(D(p(x)D) +q(x) +λ w(x))y(x) = 0

(a) The Euler equation

y(x) +λy(x)= 0

(b) The Cauchy-Euler equation



y(x)





y(x)



+λy(x)= 0