Арлоу Д., Нейштадт А. UML2 и Унифицированный процесс. Практический объектно-ориентированный анализ и проектирование

Подождите немного. Документ загружается.

536 Глава 25. Введение в OCL

• выбирать описательные имена, отражающие семантику ограниче

ния;

• гарантировать уникальность имен ограничений в рамках модели;

• имена ограничений записывать в стиле lowerCamelCase.

Определяющим операциям (init:, body:, def:, let, derive:) имя выражения

присвоить нельзя.

Семантика различных типов OCLвыражений подробно рассматрива

ется в разделе 25.10 сразу после обсуждения тела и синтаксиса OCL

выражений.

25.8. Тело выражения

Тело выражения содержит суть OCLвыражения. Простой пример пред

ставлен на рис. 25.4.

В следующих разделах мы представляем синтаксис OCL, чтобы дать

вам возможность самим научиться создавать тело OCLвыражений.

25.8.1. Комментарии, ключевые слова

и правила старшинства операций

Процессоры OCL игнорируют комментарии. Комментарии необходи

мо активно использовать, чтобы сделать OCLвыражения более понят

ными.

Комментарии необходимо активно использовать, чтобы сделать OCLвы

ражения более понятными.

Вы получите хороший комментарий OCLвыражения, если просто пе

репишете это выражение на английском (или немецком, или любом

родном вам языке). В этой главе будут приведены примеры того, как

это делается.

В OCL используется два стиля комментирования:

–– Это однострочный комментарий. Игнорируется вся строка после знака .

/* Это многострочный комментарий.

Игнорируется все, что заключено в символы комментария. */

Мы предпочитаем использовать однострочные комментарии.

В OCL есть очень небольшой набор ключевых слов, которые не могут

использоваться как имена в OCLвыражениях:

and, attr, context, def, else, endif, endpackage, if, implies, in, inv, let, not, oper, or, package,

post, pre, then, xor, body, init, derive.

Все они рассматриваются в этой главе.

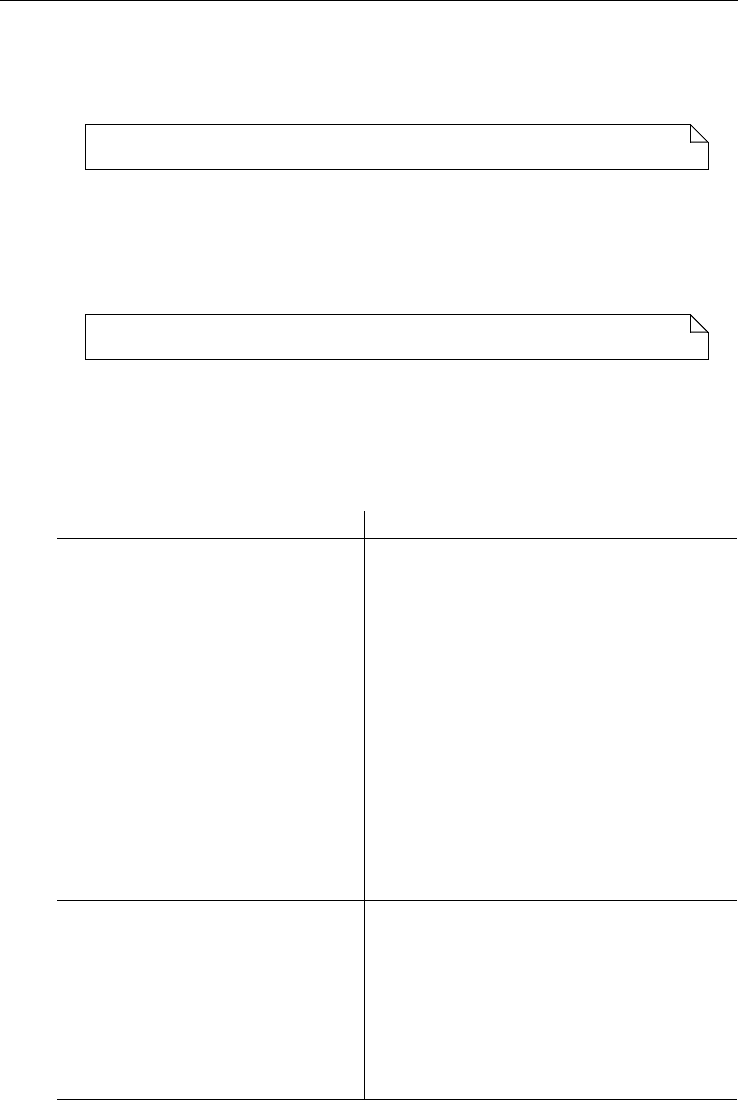
Операции OCL подчиняются правилам старшинства, как показано на

рис. 25.5.

25.8. Тело выражения 537

В любом OCLвыражении более высокие по старшинству операции вы

полняются первыми. Таким образом, например, выражение

1 + 2 * 3

в результате дает 7, потому что операция умножения * имеет более вы

сокий приоритет, чем операция сложения +.

Приоритет операций можно изменить с помощью скобок, тогда

(1 + 2) * 3

в результате дает 9.

В любом языке программирования всегда лучше использовать скобки,

а не полагаться на правила старшинства операций!

25.8.2. Система типов OCL

OCL – строго типизированный язык. Для написания OCLвыражений

необходимо понимать систему типов OCL.

Простые типы OCL – это Boolean, Integer, String и Real.

Все языки программирования имеют набор простых типов, и OCL не

исключение.

Простые типы – это Boolean, Integer, Real и String. Они обсуждаются

в разделе 25.8.3. В OCL также есть структурированный тип, Tup le (кор

теж), который рассматривается в разделе 25.8.4.

Кроме простых типов и Tup le OCL имеет ряд встроенных типов, кото

рые перечислены ниже.

• OclAny – супертип всех типов OCL и ассоциированной UMLмодели;

• OclType – подкласс OclAny – перечисление всех типов ассоциирован

ной UMLмодели;

• OclState – подкласс OclAny – перечисление всех состояний ассоцииро

ванной UMLмодели;

@pre

. –>

not – ^ ^^

* /

+ !

if ... then ... else ... endif

> < <= >=

= <>

and or xor

implies

старшинство в порядке убывания

Рис. 25.5. Приоритет операций

538 Глава 25. Введение в OCL

• OclVoid – тип «null» в OCL – имеет единственный экземпляр под на

званием OclUndefined;

• OclMessage – представляет сообщение (раздел 25.12.4).

Все классификаторы UMLмодели доступны OCLвыражениям.

Необычный, но ключевой аспект системы типов OCL состоит в том, что

все классификаторы ассоциированной UMLмодели становятся типа

ми в OCL. Это означает, что OCLвыражения могут напрямую ссылать

ся на классификаторы ассоциированной модели. Это то, что позволяет

OCL выполнять роль языка ограничений.

OclAny – супертип всех типов OCL.

В OCL все типы – это подтипы OclAny. Простые типы являются прямыми

подтипами OclAny, тогда как типы UMLмодели являются подклассами

OCLType, который, в свою очередь, является подклассом OclAny. Каждый

тип наследует небольшой набор полезных операций (табл. 25.2).

Таблица 25.2

Операция OclAny Семантика

Операции сравнения

a = b Возвращает true, если a – тот же объект, что

и b, в противном случае возвращает false.

a <> b Возвращает true, если a не тот же объект,

что и b, в противном случае возвращает

false.

a.oclIsTypeOf( b : OclType ) : Boolean Возвращает true, если a того же типа, что

и b, в противном случае возвращает false.

a.oclIsKindOf( b : OclType ) : Boolean Возвращает true, если a того же типа, что

и b, или a – подтип b.

a.oclInState( b : OclState ) : Boolean Возвращает true, если a находится в таком

же состоянии, что и b, в противном случае

возвращает false.

a.oclIsUndefined() : Boolean Возвращает true, если a = OclUndefined.

Операции запроса

A::allInstances( ) : Set(A) Это операция уровня класса, возвращаю

щая Set всех экземпляров типа A.

a.oclIsNew( ) : Boolean Возвращает true, если a был создан в ходе

выполнения операции.

Может использоваться только в постусло

виях операции.

25.8. Тело выражения 539

Вероятно, самая необычная операция OclAny – allInstances() (все экземп

ляры). Это операция уровня класса (применяется непосредственно

к классу, а не к конкретному экземпляру), она возвращает Set всех эк

земпляров данного класса, существующих на момент вызова этой опе

рации. Ни в одном из широко используемых языков программирова

ния нет такой встроенной возможности, поэтому спецификация OCL

определяет allInstances() как необязательную для реализации операцию

в инструментальных средствах, работающих с OCL. Это означает, что

ваш инструмент OCL, возможно, не сможет интерпретировать выра

жения, использующие allInstances().

В начале может показаться странным, что все типы, тщательно опреде

ленные в UMLмодели, при использовании в OCLвыражениях автома

тически получают новый супертип, OclType. Однако OCL был вынужден

сделать это, чтобы обеспечить общий объектный протокол (определен

ный OclAny), который он может использовать для работы с типами.

25.8.3. Простые типы

Простые типы OCL – это Boolean, Integer, Real и String. Их семантика во

многом аналогична семантике этих типов в других языках програм

мирования (табл. 25.3).

Таблица 25.3

Поскольку OCL является языком моделирования, а не языком про

граммирования, его спецификация не налагает ограничений на длину

строк (String), размер целых (Integer), размер и точность действитель

ных чисел (Real).

Операция OclAny Семантика

Операции преобразования

a.oclAsType( SubType ) : SubType Возвращает результат приведения a к типу Sub

Type.

Это операция приведения, и объект a может

быть приведен только к одному из его подти

пов или супертипов.

Приведение к супертипу обеспечивает доступ

к переопределенным возможностям супертипа.

Базовый тип OCL Семантика

Boolean Может принимать значения true или false

Integer Целое число

Real Число с плавающей точкой

String Последовательность символов

Строковые литералы заключаются в одинарные кавычки,

например 'Jim'

540 Глава 25. Введение в OCL

25.8.3.1. Тип Boolean

Тип Boolean принимает два значения: true и false. В нем имеется набор

операций, возвращающих значения типа Boolean. Двоичные операции

приведены в табл. 25.4. В данной таблице истинности представлены

результаты логических операций над значениями a и b.

Таблица 25.4

Все эти операции должны быть знакомы вам из других языков про

граммирования, кроме операции implies (импликация). Она пришла из

формальной логики и состоит из предпосылки, a, и следствия, b. Ре

зультат операции принимает значение true, если предпосылка и след

ствие имеют одно и то же значение или если предпосылка принимает

значение false, а следствие – true. Операция принимает значение false,

если предпосылка принимает значение true, а следствие – false.

Существует также унарный оператор not, представленный в табл. 25.5.

Таблица 25.5

Логические выражения часто используются в выражениях if...then...

else в соответствии со следующим синтаксисом:

if <логическоеВыражение> then

<oclВыражение1>

else

<oclВыражение2>

endif

25.8.3.2. Типы Integer и Real

Тип Integer представляет целое число, Real – число с плавающей точ

кой. Длина целых (Integer) и длина и точность действительных чисел

(Real) не ограничены. Integer и Real имеют обычный набор инфиксных

арифметических операций со стандартной семантикой:

=, <>, <, >, <=, >=, +, , *, /

Также эти типы имеют операции, описанные в табл. 25.6.

a b a = b a<>b a.and( b ) a.or( b ) a.xor( b ) a.implies( b )

true true true false true true false true

true false false true false true true false

false true false true false true true true

false false true false false false false true

anot a

true false

false true

25.8. Тело выражения 541

Таблица 25.6

25.8.3.3. Тип String

Строковые операции OCL (табл. 25.7) опятьтаки довольно стандарт

ны, аналогичный набор можно найти практически в любом языке про

граммирования.

Таблица 25.7

Синтаксис Семантика Применяется к

a.mod( b ) Возвращает остаток от деления a на b

например a = 3, b = 2, a.mod( b ) возвращает 1

Integer

a.div( b ) Возвращает лишь целую часть от деления a на b

например a = 8, b = 3, a.div( b ) возвращает 2

Integer

a.abs() Возвращает положительное a

например a = (3), a.abs() возвращает 3

Integer и Real

a.max( b ) Возвращает большее из чисел a и b

например a = 2, b = 3, a.max( b ) возвращает b

Integer и Real

a.min( b ) Возвращает меньшее из чисел a и b

например a = 2, b = 3, a.min( b ) возвращает a

Integer и Real

a.round() Возвращает Integer, ближайшее к a

Если два целых одинаково близки, возвращается

большее из них

например a = 2.5, a.round() возвращает 3, а не 2

a = (2.5), a.round() возвращает 2, а не 3

Real

a.floor() Возвращает ближайшее Integer, которое меньше

или равно a

например a = 2.5, a.floor() возвращает 2

a = (2.5), a.floor() возвращает 3

Real

Синтаксис Семантика

s1 = s2 Возвращает true, если последовательность символов s1 соот

ветствует последовательности символов s2, в противном слу

чае возвращает false

s1 <> s2 Возвращает true, если последовательность символов s1 не соот

ветствует последовательности символов s2, в противном слу

чае возвращает false

s1.concat( s2 ) Возвращает новую String, являющуюся объединением s1 и s2

например 'Jim'.concat( ' Arlow' ) возвращает 'Jim Arlow'

s1.size() Возвращает число символов (Integer) в s1

например 'Jim'.size() возвращает 3

s1.toLower() Возвращает новую строку символов (String), записанных

в нижнем регистре

например 'Jim'.toLower() возвращает 'jim'

542 Глава 25. Введение в OCL

Таблица 25.7 (продолжение)

Строки в OCL неизменны.

Строки в OCL неизменны (immutable). Это значит, что, будучи инициа

лизированными, они не могут быть изменены. Такие операции, как

s1.concat( s2 ), всегда возвращают новую строку String.

25.8.4. Тип Tuple

Объекты типа Tuple – это структурированные объекты, имеющие одну

или более именованных частей.

Объекты типа Tup le (кортеж) – это структурированные объекты, имею

щие одну или более именованных частей. Tu p l e необходимы, потому

что некоторые операции OCL возвращают несколько объектов. Tu pl e

имеют следующий синтаксис:

Tuple { имяЧ асти1:типЧасти1 = значение1, имяЧасти2:типЧасти2 = значение2, ... }

Имя и значение каждой части обязательны, тип – необязателен. Поря

док расположения частей не определен.

Вот пример Tu p l e , представляющего информацию об этой книге:

Tuple { title:String = ‘UML 2 and the Unified Process’, publisher:String = ‘Addison Wesley’ }

Части Tu ple могут быть инициализированы любым допустимым OCL

выражением. В приведенном выше примере мы использовали строко

вые литералы.

Синтаксис Семантика

s1.toUpper()

Возвращает строку символов (String), записанных в верхнем

регистре

например 'Jim'.toUpper() возвращает 'JIM'

s1.toInteger()

Преобразует s1 в значение типа Integer

например '2'.toInteger() возвращает 2

s1.toReal()

Преобразует s1 в значение типа Real

например '2.5'.toReal() возвращает 2.5

s1.substring(

start, end )

Возвращает новую String, являющуюся подстрокой s1, начи

нающуюся от символа, находящегося в позиции start и закан

чивающуюся символом в позиции end

Примечания:

* start и end должны быть типа Integer

* Первый символ в s1 имеет индекс 1

* Последний символ в s1 имеет индекс s1.size()

например 'Jim Arlow'.substring( 5, 9) возвращает 'Arlow'

25.8. Тело выражения 543

Доступ к частям Tup le осуществляется с помощью оператора «точка».

Например, следующее выражение возвращает значение 'Addison Wesley':

Tuple { title:String = 'UML 2 and the Unified Process', publisher:String =

'Addison Wesley' }.publisher

OCL – строго типизированный язык, поэтому каждый Tu pl e должен

быть определенного типа. Tup leTy pe (тип кортежа) – это анонимный тип.

Он не имеет имени и определяется неявно при создании Tup le . Однако

тип Tu pl eTy pe можно задать явно. Например, Tu pl eTy pe для приведенного

выше Tu ple может быть записан в OCL так:

TupleType { title:String, publisher:String }

Обычно явное определение Tu pleType необходимо только в случае, если

вы хотите создать коллекцию этого типа (раздел 25.8.6), например

Set( TupleType{ title:String, publisher:String} )   создает Set, который может хранить

  объекты Tuple

25.8.5. Инфиксные операторы

Как вы увидите в нескольких последних разделах, операции, ассоции

рованные с простыми типами OCL, бывают двух видов. Есть синтаксис

обычного вызова операции, например

a.toUpper()

и есть инфиксные операторы, в которых оператор располагается меж+

ду операндами, например

a < b

Инфиксные операторы синтаксически более удобны. Вместо a.less

Than( b ) записывается a < b. Такая форма более удобочитаема, особенно

в сложных выражениях.

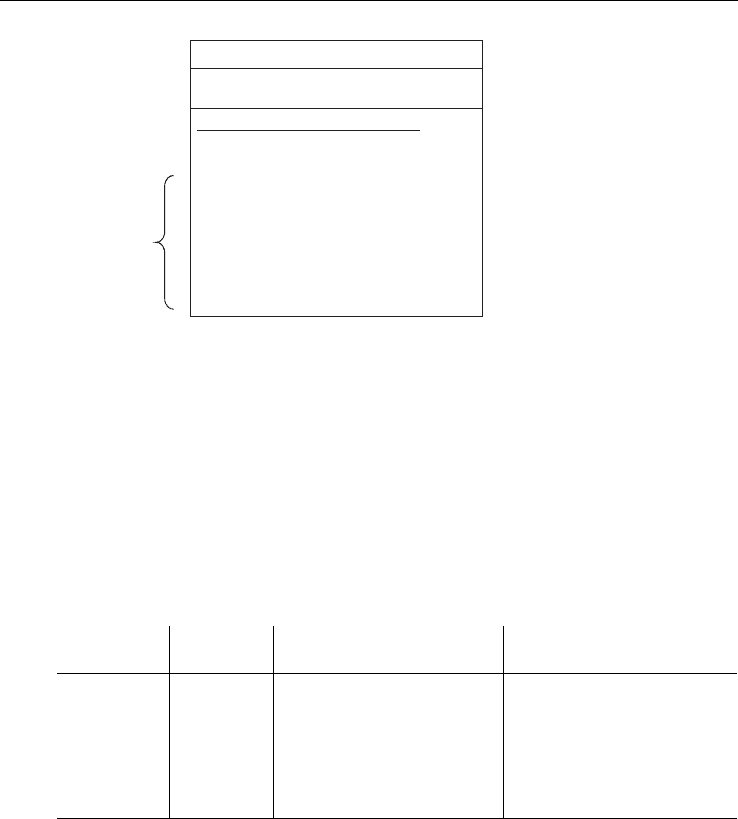
Инфиксные операторы также могут использоваться с типами из ассо

циированной UMLмодели при условии использования правильной сиг

натуры операций. Приведенный на рис. 25.6 класс Money определяет

некоторые логические и арифметические инфиксные операции.

Таким образом, если и a, и b имеют тип Money, можно использовать та

кие выражения

a < b

Однако обратите, пожалуйста, внимание, что спецификация OCL за+

прещает явные вызовы операций, такие как a.<( b ), несмотря на то,

что разумно было бы ожидать их наличия!

25.8.6. OCLколлекции

OCL предоставляет довольно обширный набор типов коллекций, кото

рые могут хранить другие объекты, включая и другие коллекции.

544 Глава 25. Введение в OCL

OCLколлекции неизменны. Это означает, что операции над коллек

циями не меняют их состояния. Например, при вызове операции для

добавления или удаления элемента коллекции эта операция возвра

щает новую коллекцию, а исходная коллекция остается неизменной.

Мы уже говорили о типах коллекций OCL в разделе 18.10. Их семан

тика сведена в табл. 25.8. Обратите внимание на соответствие каждого

из типов коллекций OCL паре свойств конца ассоциации. Применяе

мые по умолчанию свойства конца ассоциации – { unordered, unique }.

Таблица 25.8

OCLколлекции – это фактически шаблоны (раздел 17.7), для исполь

зования которых необходимо создать их экземпляр определенного ти

па. Например, OCLвыражение

Set( Customer )

создает экземпляр шаблона Set типа Customer. Тем самым определяется

шаблон Set для хранения объектов типа Customer. Можно создавать эк

земпляры OCLколлекций любого из доступных типов.

Коллекцию констант можно определить, просто перечислив в фигур

ных скобках ее элементы:

OrderedSet{ 'Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday' }

Коллекция

OCL

Упорядо

ченность

Уникальность (дублиро

вания не допускаются)

Свойства конца

ассоциации

Set Нет Да { unordered, unique } – при

меняются по умолчанию

OrderedSet Да Да { ordered, unique }

Bag Нет Нет { unordered, nonunique }

Sequence Да Нет { ordered, nonunique }

Money

Money( amount : Real, currency : String )

getAmount() : Real

getCurrency() : String

=( amount : Money ) : Boolean

<>( amount : Money ) : Boolean

<( amount : Money ) : Boolean

<=( amount : Money ) : Boolean

>( amount : Money ) : Boolean

>=( amount : Money ) : Boolean

+( amount : Money ) : Money

! ( amount : Money ) : Money

amount : Real

currency : String

Инфиксные

операторы OCL

Рис. 25.6. Инфиксные операторы OCL

25.8. Тело выражения 545

При этом автоматически создается экземпляр коллекции, тип которо

го соответствует типу перечисленных элементов.

Последовательности (Sequence) целых (Integer) литералов имеют собст

венный специальный синтаксис, использующий описание интервала

(interval specification):

Это означает: «все Integer между <start> и <end>», где <start> и <end> –

OCLвыражения, результатами которых являются Integer. Например

Sequence{ 1 ... 7} эквивалентна Sequence{ 1, 2, 3, 4, 5, 6, 7 }

Sequence{ 2 ... ( 3 + 4 ) } эквивалентна Sequence{ 2, 3, 4, 5, 6, 7 }

Коллекции могут включать другие коллекции, например

OrderedSet{ OrderedSet{ 'Monday', 'Tuesday' }, OrderedSet{ 'Wednesday','Thursday', 'Friday' } }

25.8.6.1. Операции над коллекциями

Любой единичный объект может быть интерпретирован как Set, содер

жащий только один элемент.

Коллекции обладают большим набором операций. Они должны ини

циироваться с помощью специального синтаксиса, в котором исполь

зуется оператор «стрелка»:

коллекция>операцияКоллекции( параметры... )

Этот специальный синтаксис необходим, потому что OCL может интер

претировать любой единичный объект как Set, содержащий только один

объект. Таким образом, если объект имеет, например, операцию count()

ив Set есть операция с тем же именем count(), OCL нужно както разли

чать эти две операции: принадлежащую объекту и принадлежащую кол

лекции. Это осуществляется путем использования оператора «точка»

и вызова операций над коллекциями с помощью оператора «стрелка».

В следующих нескольких разделах рассматривается семантика опера

ций над коллекциями. Чтобы было проще ссылаться на операции, мы

разбили их на следующие категории:

• операции преобразования – преобразовывают один тип коллекции

в другой (раздел 25.8.6.2);

• операции сравнения – сравнивают коллекции (раздел 25.8.6.3);

• операции запроса – получают информацию о коллекции (раз

дел 25.8.6.4);

• операции доступа – обеспечивают доступ к элементам коллекции

(раздел 25.8.6.5);

• операции выбора – возвращают новую коллекцию, содержащую

подмножество или надмножество коллекции (раздел 25.8.6.6).