Аркуша А.И. Сопротивление материалов. Раздел 2
Подождите немного. Документ загружается.

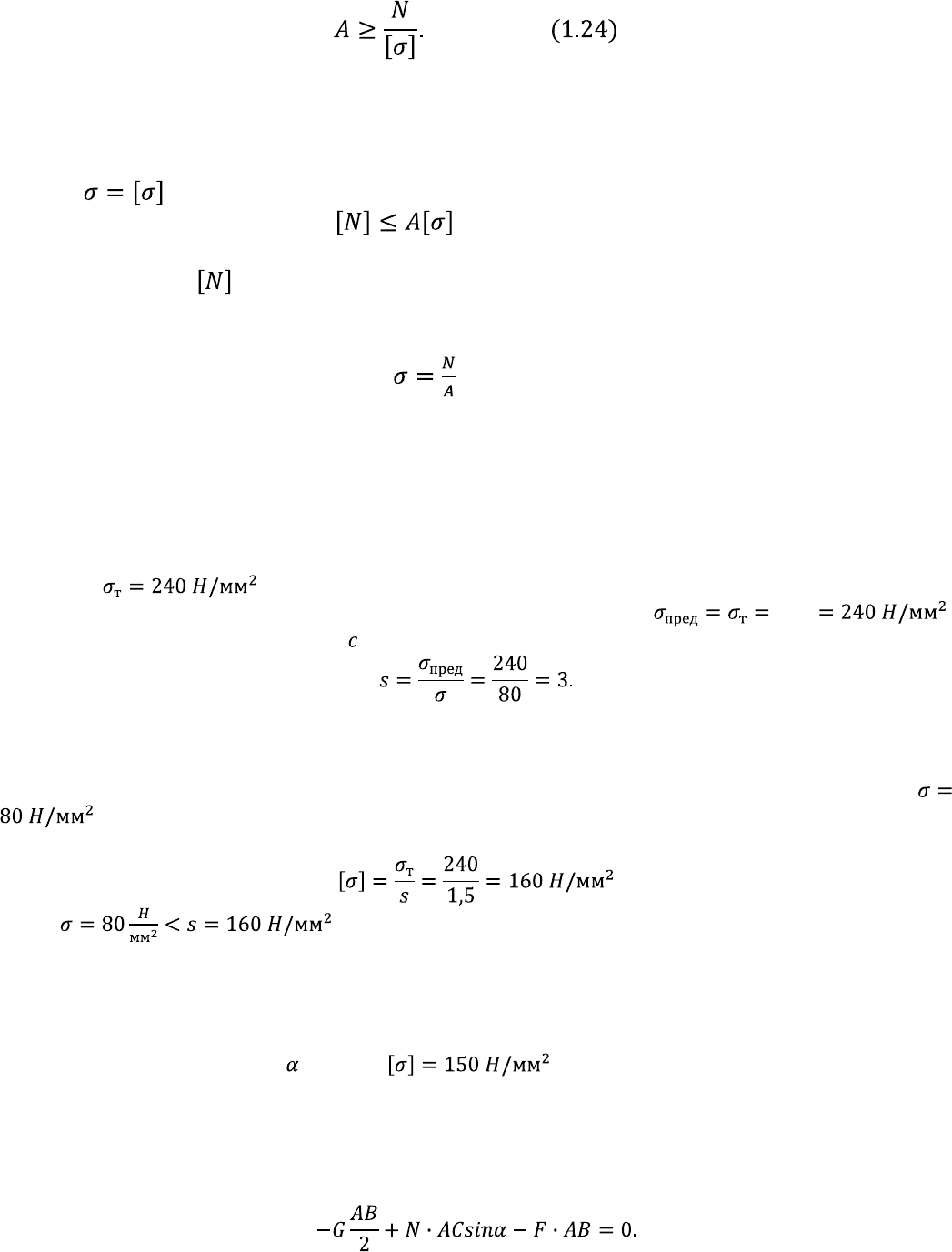
Определив из этой формулы требуемую площадь поперечного сечения, в
зависимости от формы (круг, квадрат и др.) находим его размеры.
Определение допускаемой нагрузки. В этом случае известны размеры бруса и его
материал, а требуется определить максимально допустимую нагрузку. Для этого,
приняв , из условия (1.23) находим
. (1.25)
Затем с помощью метода сечения по найденному допускаемому значению
продольной силы определяем допускаемое значение нагрузки.
Проверочный расчет. При этом расчете нагрузка бруса, его материал и размеры
известны и требуется проверить, выполняется ли условие (1.23). Для этого определяем
наибольшее расчетное напряжение в поперечном сечении бруса и сравниваем с
допускаемым. Наибольшее расчетное напряжение не должно быть больше
допускаемого, расчетное напряжение считают неопасным, если оно превышает
допускаемое не более чем на 5%. Поперечное сечение бруса, в котором возникает
наибольшее расчетное напряжение при растяжении (сжатии), называется опасным.
Пример 1.4. Проверить прочность бруса, рассмотренного в примере 1.2, если материал бруса
сталь СтЗ ( ), а требуемый коэффициент запаса прочности [s] = 1,5.
Решение 1. 1. Зная, что в данном случае предельное напряжение ,
а наибольшее расчетное напряжение , находим действительный коэффициент запаса прочности:
2. Допускаемый коэффициент запаса [s] = 1,5, значит
s = 3 > [s] = 1,5.
Условие прочности выполняется.
Решение 2. 1. Из решения примера 1.2 известно, что наибольшее расчетное напряжение
возникает в поперечных сечениях средней ступени.
2. Находим допускаемое напряжение для бруса по формуле (1.21):
3. .
Условие прочности выполняется, но брус нагружен лишь на 50%.
Пример 1.5. Однородная жесткая плита АВ силой тяжести G = 1,2 кН нагружена силой F = 8
кН (рис. 1.26, а). Определять из условия прочности диаметр стержня CD, удерживающего плиту в
горизонтальном положении; = 45°, . Решение. 1. Применяя метод сечений,
рассечем стержень CD, отбросив верхнюю его часть вместе с шарниром D, заменим их действие на
оставшуюся часть нормальной силой N (рис. 1.26, б). Сила тяжести плиты приложена посередине ее
длины.
2. Для определения силы М составим уравнение моментов относительно точки A всех сил,
действующих на плиту:
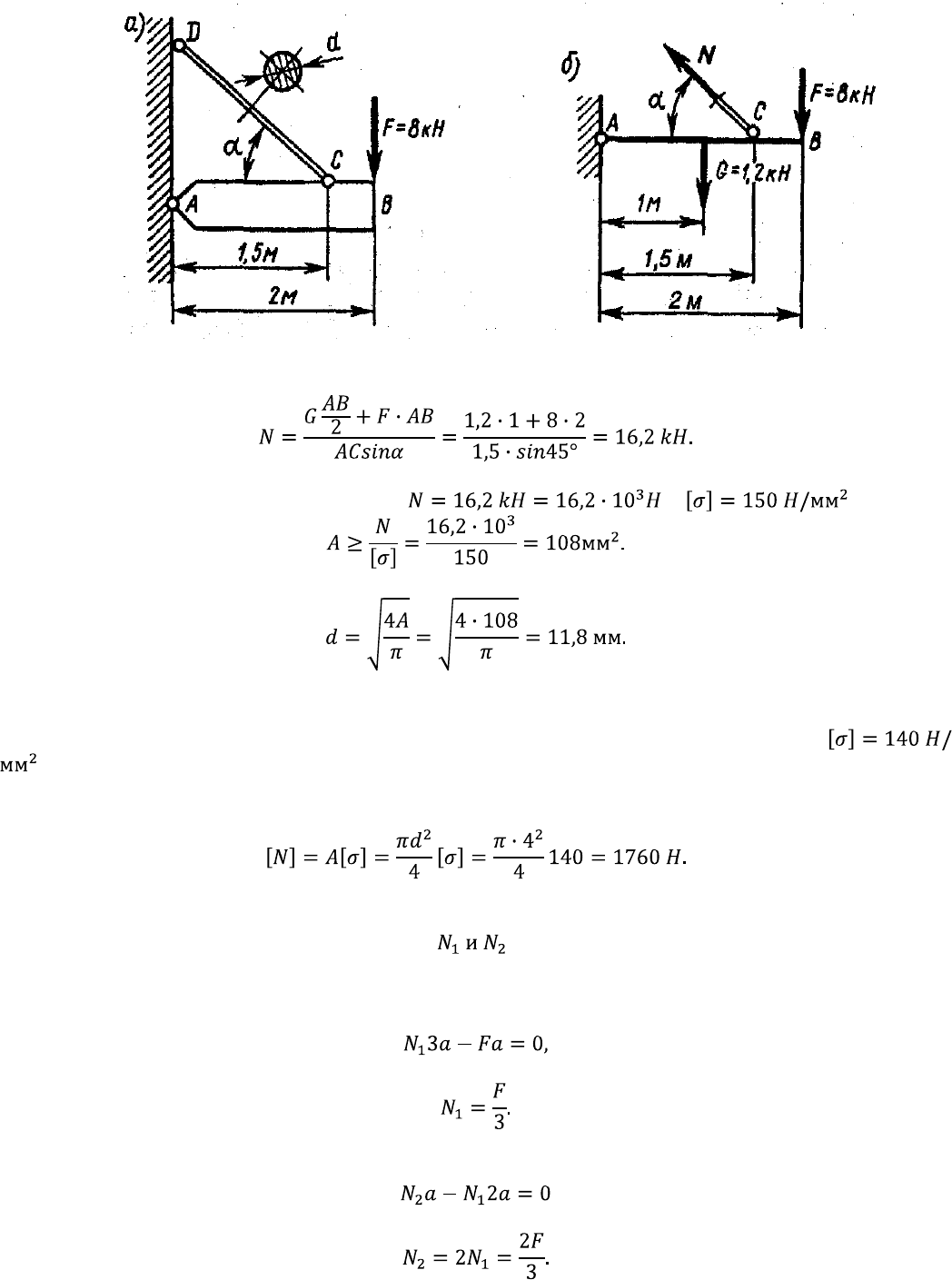
Рис. 1.26
Отсюда
3. Площадь поперечного сечения стержня, обеспечивающую его прочность, находим по
расчетной формуле (1.24), имея в виду, что и :
4. Из формулы площади круга находим диаметр стержня:
Округляя до четного числа, принимаем значение диаметра d = 12 мм.
Пример 1.6. Из условия прочности стержней 1 и 2 рычажного механизма (рис. 1.27, а)
определить допускаемую нагрузку F, если диаметры стальных стержней d = 4 мм и
.
Решение. 1. По расчетной формуле (1.25) находим максимально допускаемое значение
продольной силы:
2. Нормальные силы в поперечных сечениях, возникающие при эксплуатации механизма,
выразим через нагрузку F. для этого рассечем оба стержня и изобразим (рис. 1.27, б, в) рычаги DEC и
АВ отдельно друг от друга. Нормальные силы в стержнях рассматриваем как реакции связей,
приложенные к рычагам.
3. Из условия равновесия рычага АВ (рис. 1.27, в), т. е. из уравнения моментов сил относительно
точки В
Имеем
Из условия равновесия рычага DEC (из уравнения моментов сил относительно точки D) (рис.
1.27, б)
Получим
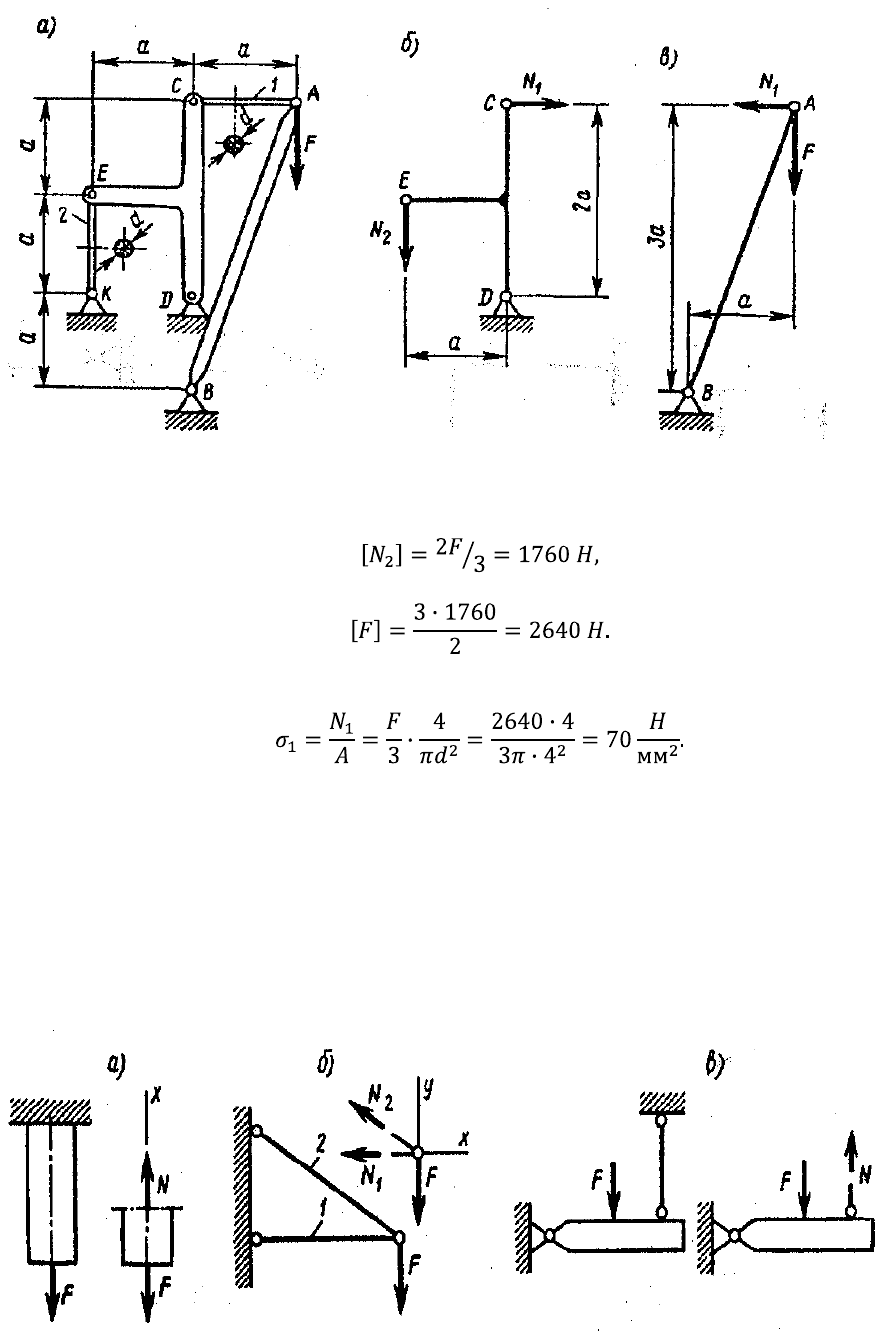
Рис. 1.27
4. Значение допускаемой нагрузки определяем исходя из условия прочности более нагруженного
стержня 2:
Откуда
При этой нагрузке механизма стержень 1 недогружен. В его поперечном сечении нормальное
напряжение
§ 1.11. Статически неопределимые системы
Механическая система, для которой реакции связей и внутренние силовые факторы
не могут быть определены с помощью уравнений равновесия статики и метода
сечений, называется статически неопределимой. Статически неопределимые системы
отличаются от статически определимых большим числом наложенных связей.
На рис. 1.28 показаны статически определимые системы, нормальные силы N в
которых определяются с помощью одного уравнения проекций на ось
Рис. 1.28
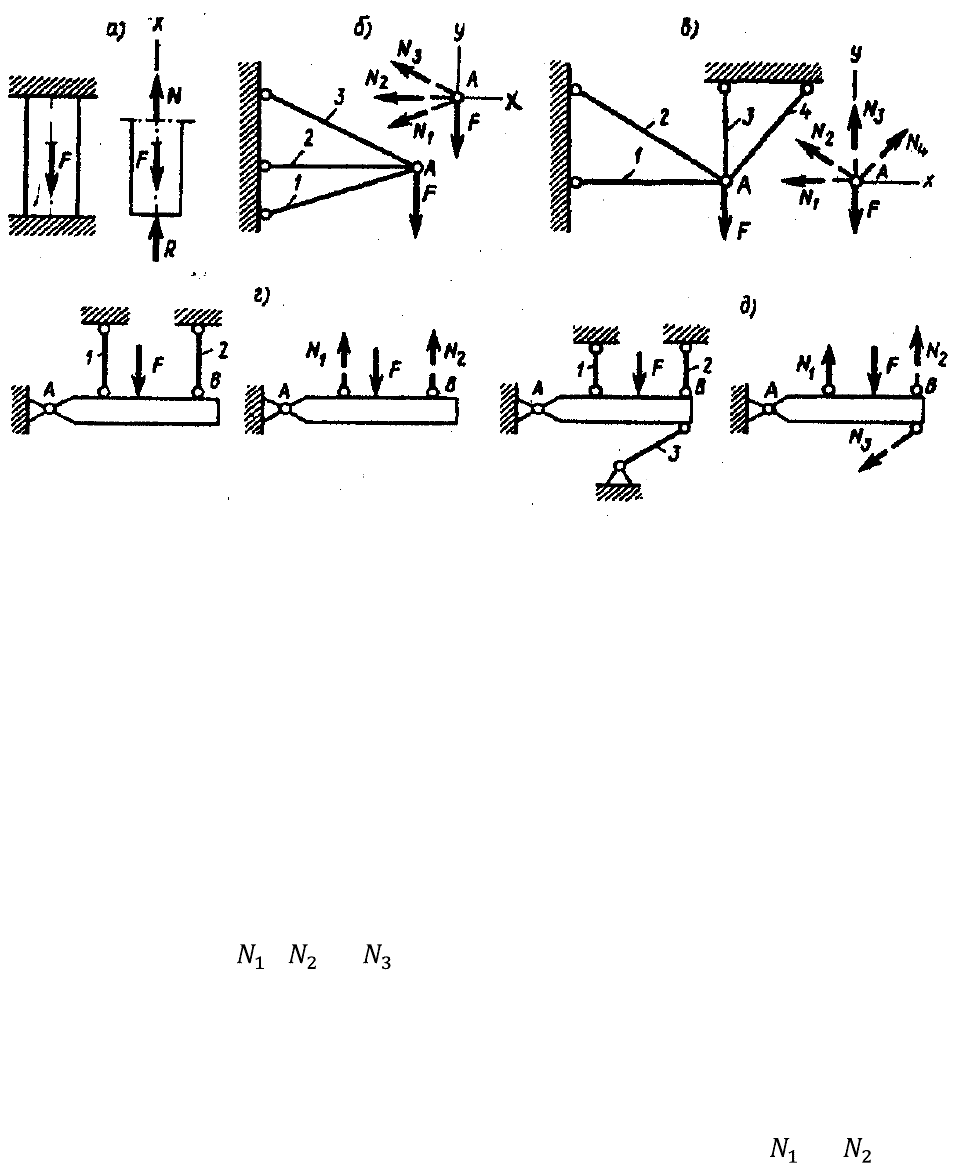
Рис. 1.29
x(a), двух уравнений проекций на оси x и y (б), одного уравнения моментов
относительно неподвижного шарнира (в). На рис. 1.29 показаны статически
неопределимые системы. Нормальная сила N в поперечном сечении бруса, жестко
заделанного с обоих концов (рис. 1.29, а), не может быть определена из уравнения
проекций на ось x, так как в него входят две неизвестные величины — нормальная
сила N и реакция R. Системы с числом неизвестных сил, на единицу превышающих
число уравнений статики, которые можно составить для этой системы, называются
один раз статически неопределимыми. Чтобы решить задачу, необходимо составить
дополнительное уравнение перемещений из условия, что общая длина бруса остается
неизменной.
Система на рис. 1.29, б также один раз статически неопределима, так как в два
уравнения проекций сил, которые можно составить в данном случае, входят три
неизвестные величины: , и . Система на рис. 1.29, в два раза статически
неопределима — в те же два уравнения статики входят четыре неизвестные. Для
решения этих задач в первом случае нужно составить одно дополнительное уравнение
перемещений, а во втором — два, исходя из условия, что при изменении длины
стержней узел A остается для них общим.
Система на рис. 1.29, г один раз статически неопределима и к уравнению моментов
сил относительно точки A, содержащему две неизвестные силы ( и ), нужно
дополнительно составить одно уравнение перемещений. На рис. 1.29, д изображена
два раза статически неопределимая система и дополнительных уравнений
перемещений необходимо составить два. В подобных случаях уравнения перемещений
составляют из условия, что места закрепления стержней балке АВ остаются на одной
прямой.
Вообще говоря, если число неизвестных сил системы на n превышает число
уравнений статики, которые можно составить для нее, то система называется n раз
статически неопределимой и для решения задачи необходимо составить n уравнений
перемещений.
В статически неопределимых системах иногда необходимо считаться с
напряжениями, возникающими при изменении температуры системы в целом или
отдельных ее элементов. Так, например, в стержне, жестко заделанном с обоих концов
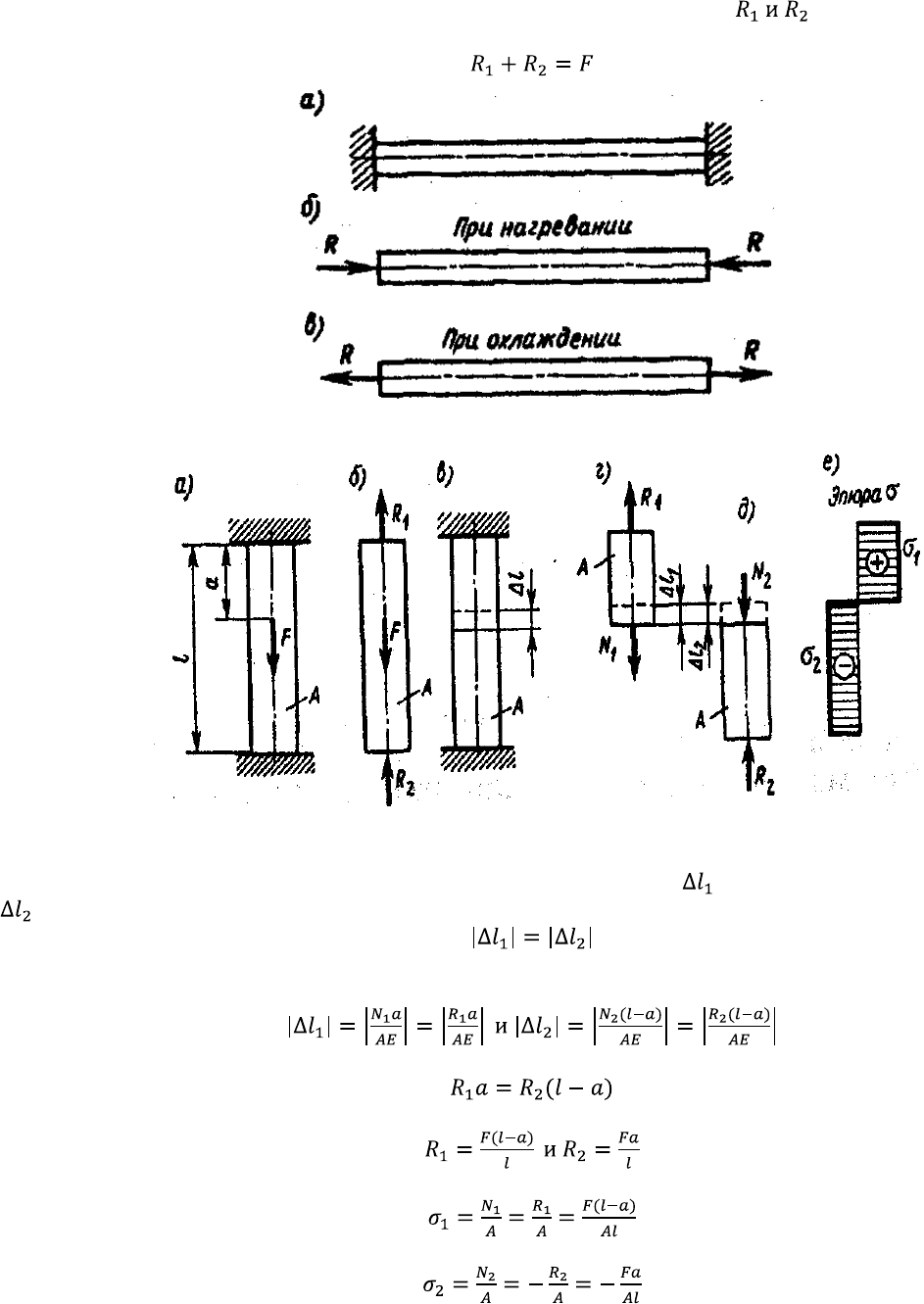
в неподатливых стенках (рис. 1.30, а), при нагревании возникают напряжения сжатия
(рис. 1.30, б), а при охлаждении — напряжения растяжения (рис. 1.30, в).
Пример 1.7. Брус постоянного поперечного сечения площадью A жестко закреплен с обоих
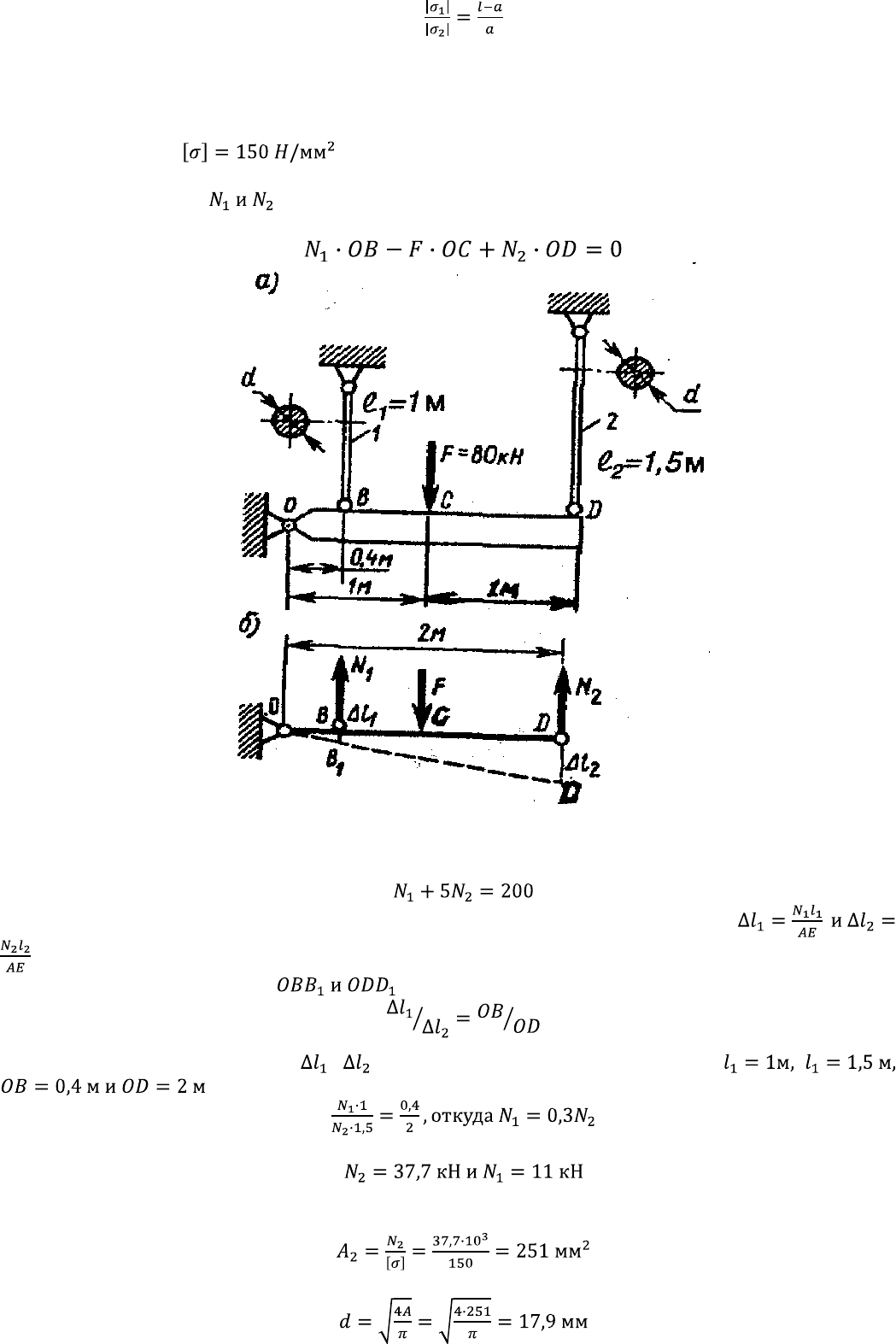
концов и нагружен силой F, как показано на рис. 2.31. а. Определить напряжения, возникшие в
поперечных сечениях верхней и нижней частей бруса.
Решение. 1. Действие связей на брус изобразим реакциями (рис. 1.31, б). Для
образовавшейся системы сил составим уравнение статики,
,
Рис. 1.30
Рис. 1.31
в которое входят две неизвестные силы. Система один раз статически неопределима
2. Под действием силы F верхняя часть бруса растянулась на , нижняя часть укоротилась на
, (рис. 1.31, в, е, д). Так как общая длина бруса осталась неизменной, то
.
Это и есть уравнение перемещений.
3. Из рис. 1.З1, г, д следует, что
.
Левые части этих равенств равны между собой, значит, равны и правые части, т. е.
.
Решая это уравнение совместно с уравнением статики, находим
.
5. Напряжения в поперечных сечениях верхней растянутой части бруса
.
6. Напряжения в поперечных сечениях нижней сжатой части бруса
.
7. Сопоставляя полученные значения напряжений в частях бруса, легко заметить, что
.
8. Эпюра напряжений по длине бруса показана на рис. 1.31, е.
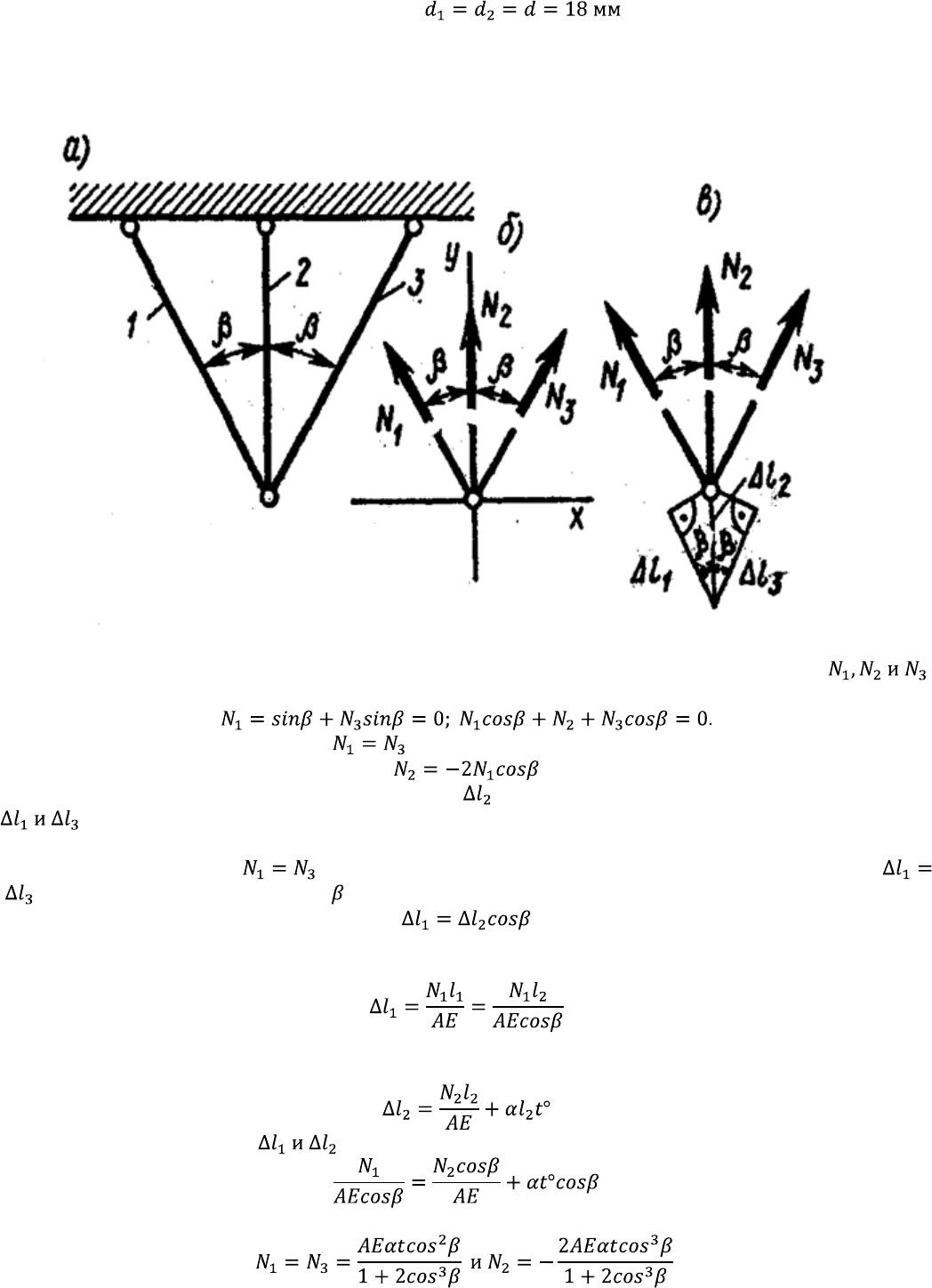
Пример 1.8. Жесткий брус удерживается в равновесии двумя стальными стержнями круглого
поперечного сечения одного и того же диаметра (рис. 1.32, а). Определить необходимые диаметры
этих стержней, если .
Решение. 1. Рассекая стержни и заменяя действие их отброшенных частей на жесткий брус
нормальными силами , получаем расчетную схему (рис. 1.32, б), для которой запишем
уравнение статики (уравнение моментов сил относительно точки А):
.
Рис. 1.32
После подстановки числовых значений величин (F = 80 кН, ОВ = 0,4 м, ОС = 1 м и ОD = 2 м)
уравнение статики примет вид
.
2. Под действием силы F стержни 1 и 2 удлиняются соответственно на
(рис. 1.32, б).
Из подобия треугольников получим уравненяс перемещений
.
Подставив сюда выражения , из п. 2, а также числовые значения
, получим
.
З. Решив совместно уравнения статики и перемещений, найдем
.
4. Из условия прочности более нагруженного стержня 2 по расчетной формуле (1.24) находим
требуемую площадь поперечного сечения
.
5. Диаметр стержня
.
6. Округляя до четного числа, принимаем .
Пример 1.9. Определить, какие внутренние силы возникнут в стержневой системе (рис. 1.33,
а), если стержень 2 нагреть на t°. Все стержни изготовлены из одного материала и имеют одинаковые
площади поперечных сечений.
Рис. 1.33
Решение. 1. При деформировании системы в стержнях возникают нормальные силы .
Выбрав оси x и y, как показано на рис. 1.33, б, составим два уравнения статики:
Из первого уравнения ясно, что . Поэтому второе уравнение статики примет вид
2. При нагревании стержень 2 удлиняется на и вытягивает стержни 1 и 3 соответственно на
(рис 1.33, в).
Так как стержни изготовлены из одного материала, имеют одинаковые площади поперечных
сечений и длины, то при удлинения стержвей 1 и 3 также равны между собой, т. е.
. Уравнение перемещений (угол меняется незначительно)
3. Удлинение первого и третьего стержней происходит под действием силы со стороны стержня
2. Поэтому
Удлинение второго стержня происходят под влиянием температуры и действия на него стержней
1 и 3. Поэтому по формуле (1.13) находим
4. Подставляя значения в уравнения перемещений из п. 2, получаем
5. Решая уравнение перемещений совместно с уравнением статики, из п. 1 находим
Таким образом, стержень 2 сжат, а стержни 1 и З растянуты.
ГЛАВА 3. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НА СРЕЗ И
СМЯТИЕ
§ 1.12. Основные расчетные предпосылки и формулы
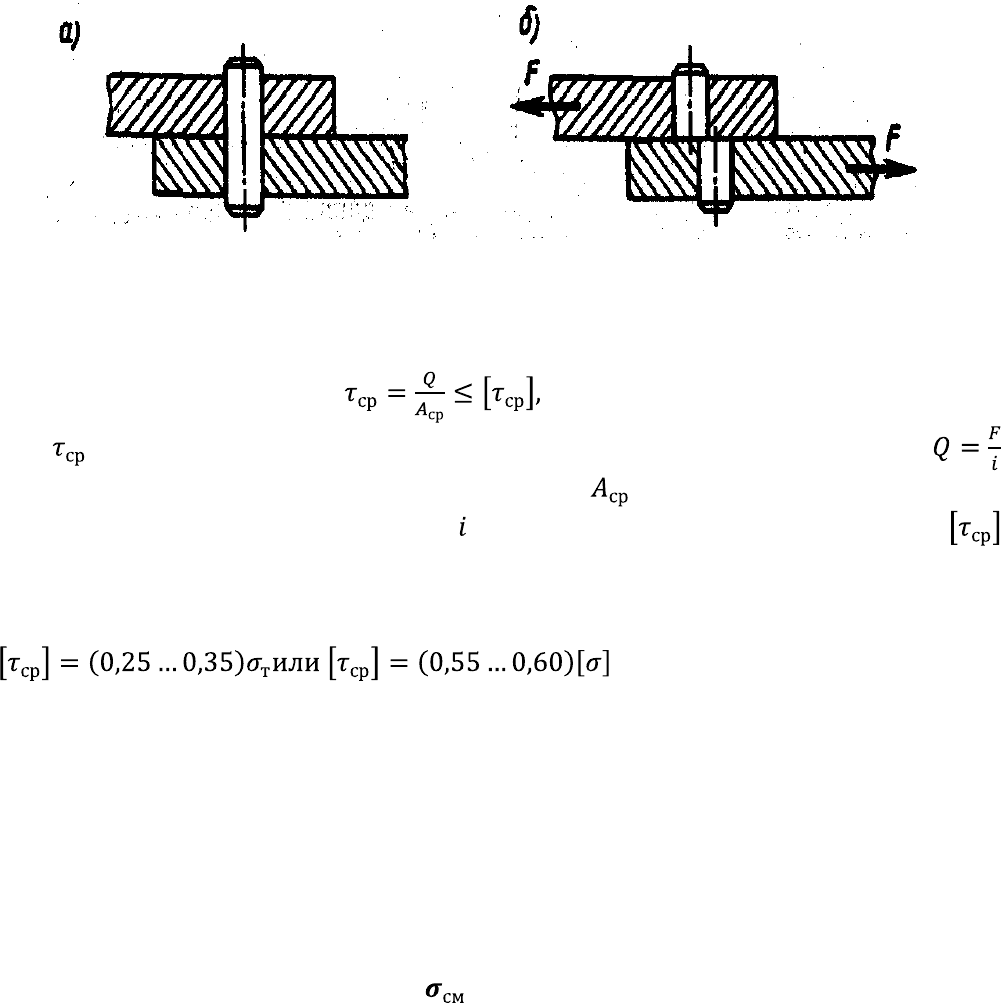
Если два бруса соединить между собой штифтом, а затем нагрузить
направленными в противоположные стороны силами F (рис. 1.34), то при
значительных силах или небольшом диаметре штифта он может быть разрушен по
сечению, расположенному в плоскости соприкасания поверхностей соединяемых
брусьев (рис. 1.34, б). Такое разрушѐние соединительных деталѐй (штифта, болта,
шпильки, заклепки, шпонки), происходящее под действием нагрузок
перпендикулярных их собственным осям (поперечные нагрузки), называется срезом.
Практические расчеты соединительных деталей на срез носят условный характер и
основываются на трех допущениях: в поперечном сечении возможного среза детали
возникает только один внутренний силовой фактор — поперечная сила Q; касательные
напряжения, возникающие в поперечном сечении, распределены по сечению
равномерно; если соединение осуществлено несколькими одинаковыми деталями
(болтами, заклепками и др.), то считается, что все
Рис. 1.34
они нагружены одинаково. Исходя из этих допущений условие прочности при расчете
на срез запишется в таком виде:
(1.26)
где — расчетное напряжение среза в поперечном сечении детали; —
поперечвая сила, возникающая в этом сечении; — площадь поперечаого сечения
срезаемой детали (площадь среза); — число соедяввтельиьхх деталей; —
допускаемое напряжение при расчетах на срез, зависящее от материала
соединительной детали и условий работы конструкции.
При расчете болтов, штифтов, шпонок и прочего принимают
.
Из условия прочности (1.26) можно производить три вида расчетов: а)
проверочный; б) проектный (определение числа соединительных деталей при
заданных размерах либо определение размеров детали при заданном их числе); в)
определение допускаемой нагрузки.
При небольшой толщине соединяемых брусьев (листов) и значительной нагрузке
между поверхностью соединительной детали и стенками отверстия возникает большое
взаимное давление, в результате которого стенка отверстия может обмяться, форма
отверстия изменится и соединение разрушится.
Давление, возникшее между поверхностями соединительной детали и отверстия,
называется напряжением смятия .
Расчеты на смятие, так же как и расчеты на срез, носят условный характер.
Считают, что силы давления распределены по поверхности смятия равномерно и
перпендикулярны ей. Отсюда условие прочности на смятие имеет такой вид:
(1.27)
где - нагрузка на один соединительный элемент ( — число элементов); -
площадь смятия; — допускаемое напряжение смятия. Для низкоуглеродистой
стали
Рис. 1.35
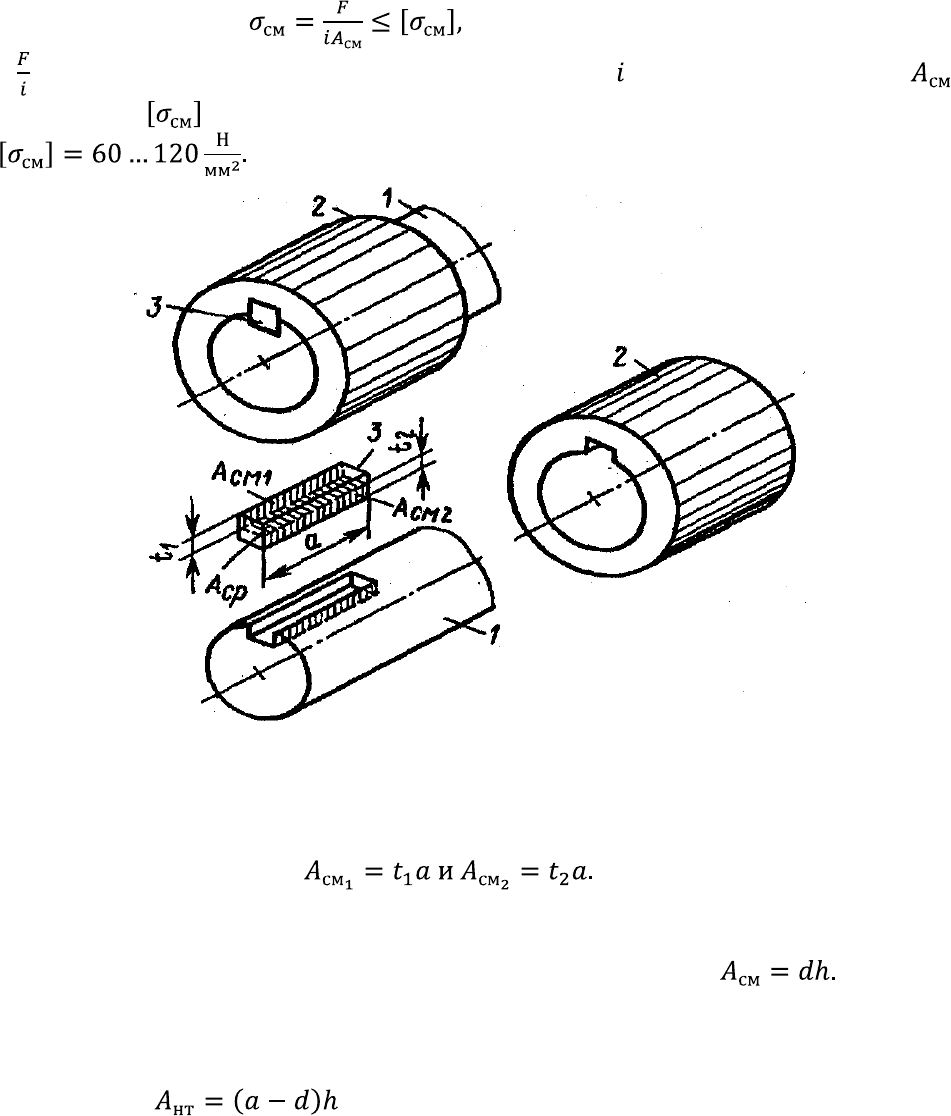
Если поверхность смятия плоская, как, например, при соединении вала 1 и втулки
2 призматической шпонкой 3 (рис. 1.35), то площадь смятия определяется
непосредственно как произведение длины на ширину:
Если поверхность смятия цилиндрическая, то в расчетную формулу (1.27)
подставляется условная площадь смятия, равная площади проекции поверхности на
диаметральную плоскость. На рис. 1.36 условная площадь смятия
Кроме проверки деталей на смятие при относительно небольшой ширине
соединяемых листов или пластин их проверяют на разрыв по поперечному сечению,
ослабленному отверстиями. На рис. 1.36 площадь ослабленного поперечного сечения
(площадь «нетто») .

Рис. 1.36
§ 1.13. Примеры расчета
Пример 2.10. Проверить прочность стержня на растяжение, его головки на срез и опорной
поверхности под головкой на смятие (рис. 1.37, а), если допускаемые напряжения
.
Решение. 1. диаметр стержня d = 5 мм, следовательно, площадь поперечного сечения стержня
а нормальная сила в этом сечении N = F =2 кН = 2000 Н. По формуле (1.23) рабочее напряжение в
поперечном сечении
2. Головка стержня может быть срезана по цилиндрической поверхности диаметром d = 5 мм и
высотой h = 2 мм (рис. 2.37, б), т. е. . Следовательно, по формуле
(2.26) при Q=F рабочее напряжение среза
Перегрузка составляет =6,33%, что недопустимо. Необходимо, либо снизить
нагрузку, либо взять стержень с более высокой головкой.
З. Поверхность контакта между головкой стержня и опорой имеет форму плоского кольца (рис.
1.37, в), т.е.
Рабочее напряжение смятия определяем по формуле (1.27):
