Аркуша А.И. Сопротивление материалов. Раздел 2
Подождите немного. Документ загружается.

5. Переходим к построению эпюры N (рис. 1.12, д). Для этого параллельно оси бруса проводим
тонкую начальную, или базовую, линию, перпендикулярно которой в определенном масштабе вправо
откладываем отрезки, изображающие положительные значения продольной силы, а влево —
отрицательные. Получившаяся ступенчатая фигура, ограниченная основной линией и
заштрихованная перпендикулярно базовой линии, и есть искомая эпюра нормальных сил по длине
бруса. «Читая» эпюру на рис. 1.12, д, например, сверху вниз, видим: на участке DC брус растянут,
нормальная сила, равная 0,5F, постоянна до сечения C (эпюра N на участке параллельна базовой
линии); при переходе через сечение C эпюра делает «скачок», равный абсолютному значению
приложенной в этом сечении силы; правая (положительная) часть скачка (+0,5F) изображает
значение нормальной силы чуть выше сечения C. а левая (отрицательная) часть скачка (-F)
изображает значение нормальной силы чуть ниже сечения C (т. е. относится к участку CB), а далее
постоянное значение нормальной силы -F сохраняется во всех поперечных сечениях бруса вплоть до
сечения B; при переходе через сечение B эпюра снова испытывает скачок от значения -F до +F,
характеризующий переход от сжатого участка CB к растянутому BA. Абсолютное значение скачка
равно силе 2F, приложенной к брусу в этом сечении. В заключение заметим, что скачки на эпюрах по
абсолютному значению всегда равны модулям внешних сил, приложенных в этом месте к брусу.
Переходим теперь к определению напряжений в поперечных сечениях бруса.
Эта задача решается на основе гипотезы плоских сечений, высказанной Я.
Бернулли старшим (1654—1705). Применительно к рассматриваемому виду
нагружения гипотеза гласит: перпендикулярное оси недеформированного бруса
плоское сечение A (рис. 1.13, а) остается таким же плоским и перпендикулярным оси и
при растяжении (сжатии) бруса (рис. 1.13, б). Исходя из того что в растянутом
(сжатом) брусе поперечные сечения остаются параллейными друг другу, естественно
предположить, что внутренние силы распределены по сечению равномерно (рис. 1.13,
в), а так как нормальная сила N является равнодействующей внутренних сил в
поперечном сечении, нормальное напряжение в любой точке сечения
(1.6)
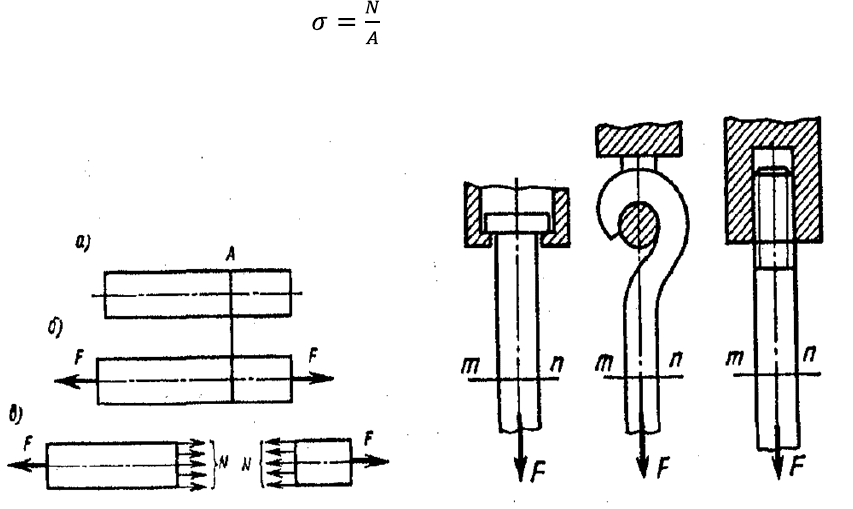
где A — площадь поперечного сечения. Нормальное напряжение направлено так же,
как и нормальная сила: при растяжении бруса — от сечения, при сжатии — к сечению.
Рис. 1.13 Рис. 1.14
Рассматривая растяжение бруса осевыми силами, приложенными к его торцам, мы
не касались вопроса о том, каким способом растягивающие силы приложены к брусу.
При любом из способов (рис. 1.14) вблизи закреплений брус испытывает более
сложный вид нагружения, чем простое растяжение. Вместе с тем теоретические
соображения, подтверждаемые экспериментальными исследованиями, показывают,
что особенности приложения внешних сил к растянутому брусу влияют на
распределение напряжений в его поперечных сечениях только вблизи места
нагружения.
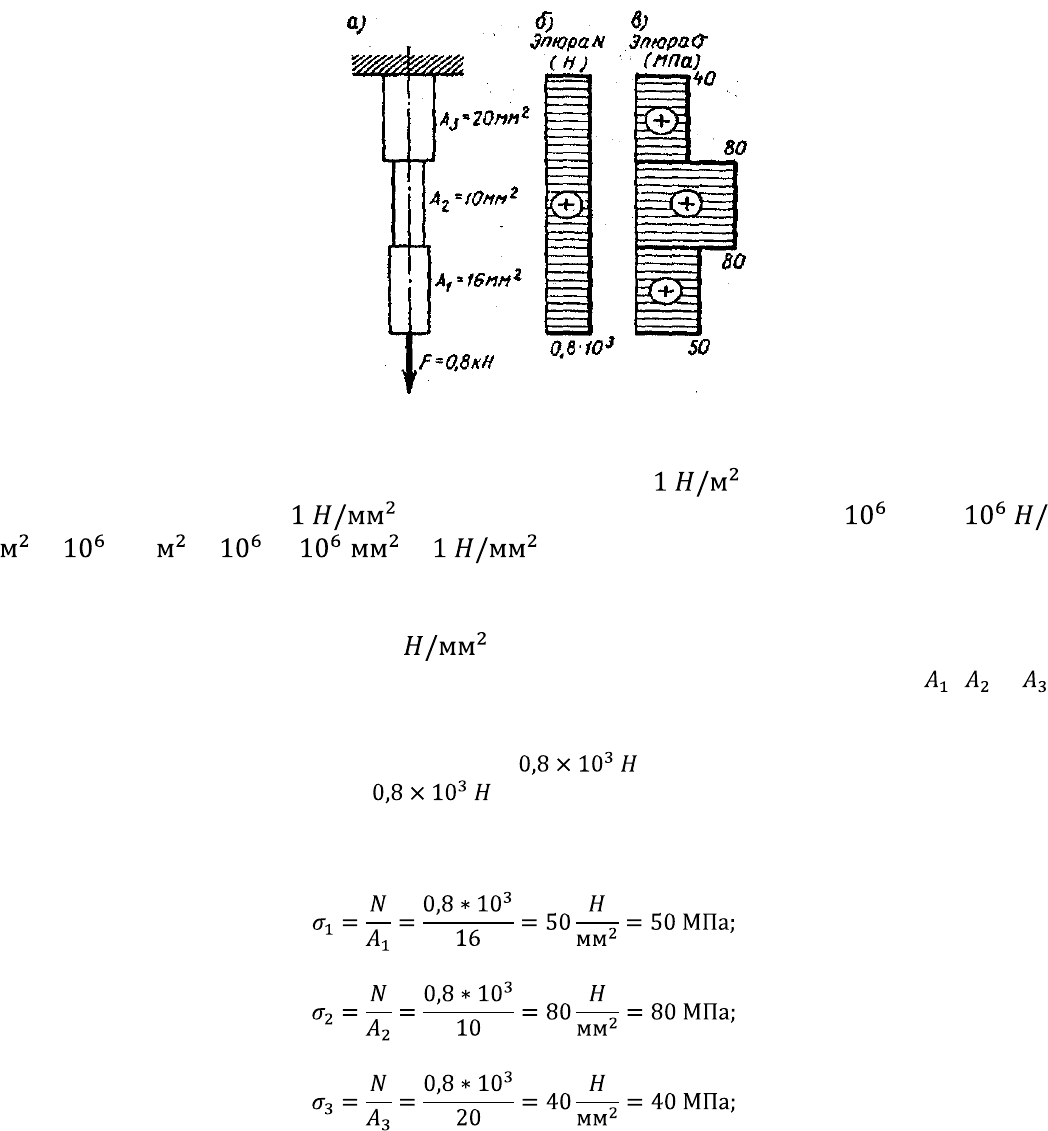
В поперечных сечениях m-n (рис. 1.14) на расстоянии, превышающем их
наибольшие размеры, при определении нормальных напряжений достаточно
принимать во внимание только значение заданной осевой силы F и площадь
сечения А.
Это положение известно как принцип Сен-Венана в применении к растяжению
(сжатию) бруса.
Применяя этот принцип, в дальнейшем, мы не будем принимать во внимание
конкретный способ приложения к брусу внешних сил. Если нормальные напряжения в
разных сечениях бруса не одинаковы либо из-за изменения нормальных сил вдоль оси
бруса (см. пример 1.1), либо из-за изменения площади поперечных сечений, то строят
эпюру нормальных напряжений (эпюра σ), которая наглядно характеризует
напряженное состояние бруса по всей его длине.
Рис. 1.15
При практических расчетах, связанных с определением напряжений в сечениях
бруса, вместо единицы напряжений 1 Па = удобнее использовать
внесистемную единицу , численно равную 1 МПа (1 МПа = Па =
= Н/1 = Н/ = ), так как в технических расчетах размеры
поперечных сечений рассчитываемых деталей машин, как правило, выражают в
миллиметрах. Учитывая это обстоятельство, механические характеристики материалов
будем в дальнейшем выражать в .
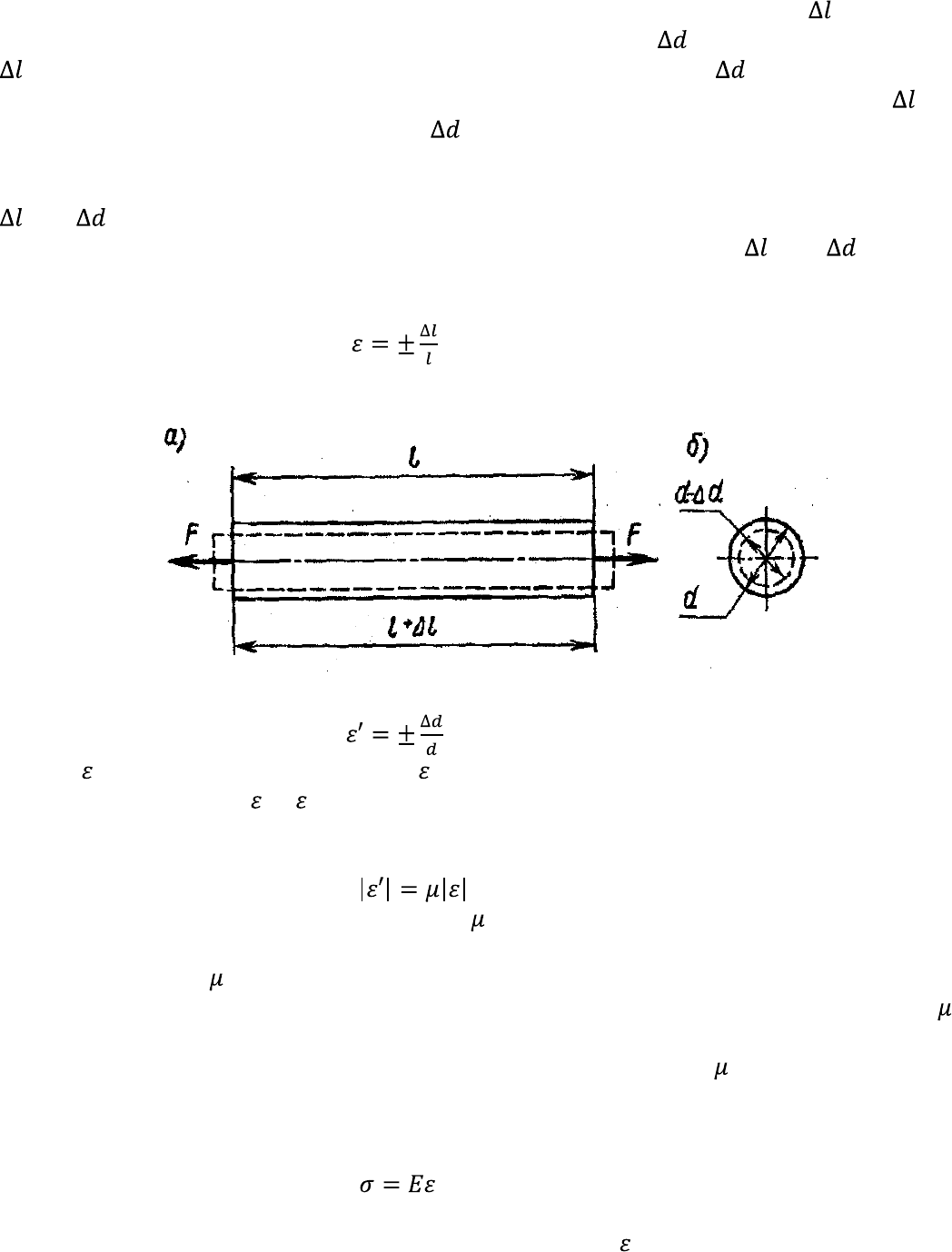
Пример 1.2. Трехступенчатый брус с площадями поперечных сечений ступеней , и
нагружен силой F, как показано на рис. 1.15, а. Определить нормальные напряжения в поперечных
сечениях и построить эпюру σ по длине бруса.
Решение. 1. Брус растянут силой F = 0,8 кН = . Применяя метод сечений, определяем,
что в любом сечении бруса N = F = . Эпюра N изображена на рис. 1.15, б.
2. Площади поперечных сечений ступеней заданы. Подставляя их значения в формулу (1.6),
находим нормальные напряжения:
в поперечном сечении нижней ступени
в поперечном сечении средней ступени
в поперечном сечении верхней ступени
З. Эпюра нормальных напряжений по всей длине бруса изображена на рис. 1.15, в.
Построение эпюры не может вызвать затруднений. Нормальные напряжения в поперечных
сечениях одной ступени не изменяются. Поэтому эпюра σ для каждой ступени изображается
отрезком, параллельным базовой линии; расстояния между этими отрезками и базовой линией
пропорциональны нормальным напряжениям в сечениях ступеней.
§ 1.7. Перемещения и деформации. Закон Гука.
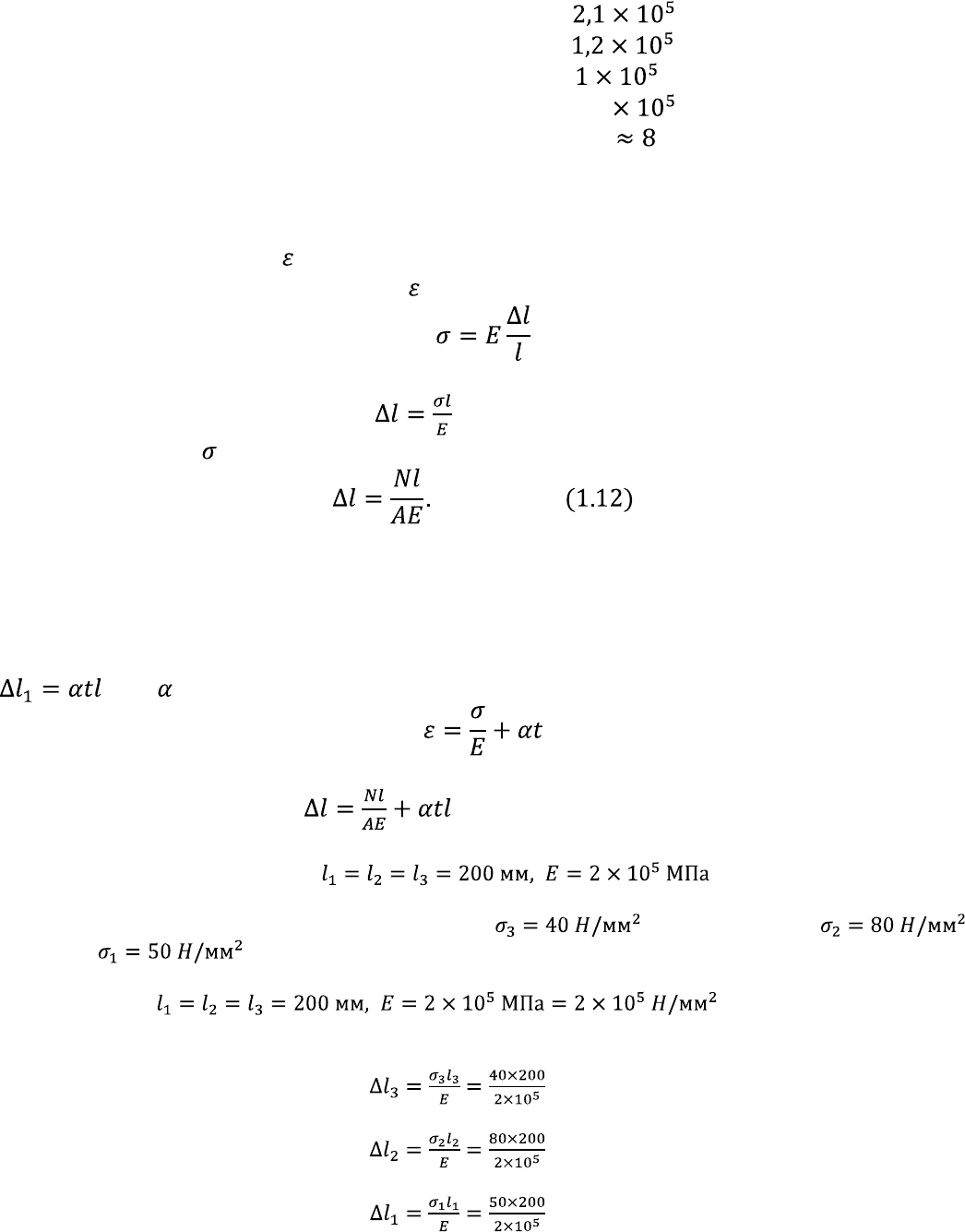
При растяжении бруса его первоначальная длина l увеличивается на (рис. 1.16,
а), а первоначальный поперечный размер d уменьшается на (рис. 1.16, б). Величина
называется абсолютным удлинением бруса, а величина — абсолютным
поперечным сужением. При сжатии бруса его длина укорачивается на , а
поперечный размер увеличивается на . Рассматривая любую из этих величин как
разность между начальным (до нагружения) и конечным (после нагружения)
размерами им следует приписывать противоположные знаки: при растяжении бруса
> 0, < 0, при сжатии наоборот.
О степени деформирования бруса нельзя судить по значениям или , так как
последние зависят не только от внешних сил, но и от начальных размеров бруса.
Деформирование бруса при растяжении (сжатии) характеризуют величины
(1.7)
Рис. 1.16
(1.8)
где — продольная деформация, ’ — поперечная деформация бруса. Из формул
(1.7) и (1.8) видно, что и ’ — величины безразмерные.
Экспериментально доказано, что продольная и поперечная деформации
пропорциональны друг другу, т. е.
, (1.9)
где коэффициент пропорциональности , зависящий от материала, называется
коэффициентом Пуассона. Его значение для разных материалов колеблется в пределах
0...0,5; у пробки = 0 (при растяжении или сжатии пробочного брусочка его
поперечные размеры практически не изменяются); у каучука (резины) значение
близко к 0,5 (при растяжении резинового бруса его поперечные размеры заметно
уменьшаются, при сжатии — заметно увеличиваются); для стали = 0,25...0,3.
В пределах упругих деформаций между нормальным напряжением и продольной
деформацией существует прямопропорциональная зависимость, носящая название
закона Гука.
(1.10)
Коэффициент пропорциональности E называется модулем упругости, и его
значение выражается в единицах напряжения, так как — величина безразмерная.
Значения E для некоторых материалов, МПа:
Стали всех марок…………………………………….
Медь техническая…………………………………….
Бронза оловянистая…………………………………..
Алюминиевые сплавы………………………………….0,7
Каучук (резина)………………………………………..7,85
Модуль упругости характеризует жесткость материала,. т. е. способность
сопротивляться деформациям: согласно закону Гука [см. формулу (1.10)], при одних и
тех же значениях нормального напряжения в поперечных сечениях брусьев их
продольные деформации тем меньше, чем больше модуль упругости Е.
Если в равенстве (1.10) заменить выражением из формулы (2.7)
то получим выражение
(1.11)
Заменив здесь его выражением из формулы (1.6), получим
Стоящее в знаменателе произведение АЕ называется жесткостью сечения бруса
при растяжении (сжатии), а выражение АЕ/l— жесткостью бруса или отдельного его
участка при растяжении.
При решении некоторых практических задач возникает необходимость наряду с
удлинениями при растяжении (сжатии) учитывать также и температурные удлинения
, где — коэффициент линейного расширения материала. В этом случае
и
(1.13)
Пример 1.3. Определить полное удлинение бруса, рассмотренного в примере 1.2 (см. рис.
1.15), если длины ступеней бруса .
Решение. 1. При решении задачи в примере 2.2 построена эпюра (см. рис. 1.15, в), из которой
видно, что в поперечном сечении верхней ступени , средней ступени
и нижней . Длины ступеней и модуль упругости известны. Поэтому для определения
удлинения ступеней бруса целесообразно воспользоваться формулой (1.11).
2. Так как , то удлинения ступеней
бруса равны:
Верхней
=0,04 мм;
Средней
=0,08 мм;
Нижней
=0,05 мм.
3. Определив удлинения ступеней, можно построить эпюру перемещений сечений. Для этого
рядом с чертежом бруса (рис. 1.17, а) параллельно его оси проводим базовую линию, а перемещения
сечений изображаем перпендикулярными к ней отрезками, взятыми в определенном масштабе.

Рис. 1.17
Перемещение сечения в заделке равно нулю, т. е. ; перемещение сечения D равно
удлинению верхней ступени бруса, т. е. ; перемещение сечения C равно сумме
удлинений верхней и средней ступеней бруса, т. е. ;
перемещение сечения B равно сумме удлинений всех трех ступеней, иначе говоря, полному
удлинению бруса , т. е. мм
Соединив концы отрезков, изображающих перемещения рассмотренных сечений прямыми,
получим эпюру перемещений по всѐй длине бруса (рис. 1.17, б).
§ 1.8. Напряженное состояние при одноосном растяжении.
Напряженное состояние в точке характеризуется всем бесчисленным
множеством нормальных и касательных напряжений, возникающих на
площадках, которые можно провести через эту точку.
Для исследования напряженного состояния бруса при растяжении силами,
действующими вдоль его оси (одноосное растяжение), выберем какую-либо точку B
(рис. 1.18, а) и изобразим ее в виде малого элемента в форме прямоугольного
параллелепипеда отдельно от бруса (рис. 1.18, б). Если предположить, что брус
состоит из бесконечно большого числа очень тонких продольных волокон и считать,
что все эти волокна не надавливают друг на друга, а только растягиваются (гипотеза о
ненадавливании волокон), то можно сделать вывод, что на гранях параллелепипеда,
параллельных поперечным сечениям бруса, возникают только нормальные
напряжения, а остальные грани от напряжений свободны.
Рис. 1.18

Разрежем выделенный элемент по сечению (на рис 1.18, б оно заштриховано),
нормаль On к которому образует с осью z угол , и отбросим часть элемента правее
сечения. Оставленная левая часть (рис. 1.18, в) сохраняет равновесие, так как сила
, действующая на перпендикулярную оси x площадку , уравновешивается силой
, действующей на наклонную к оси z площадку , т.е.
.
Следовательно, возникшее на наклонной площадке полное напряжение
Разложим напряжение p на две составляющие по нормали On и касательной Ot
(рис. 1.18, г), находим
Подставим сюда вместо p его значение из уравнения (1.14) и с учетом того, что
, получим
; (1.15)
. (1.16)
Таким образом, зная нормальное напряжение σ в поперечном сечении растянутого
(сжатого) бруса, можно по формулам (1.15) и (1.16) определить нормальное и
касательное напряжения в сечении бруса, наклоненном к оси бруса под любым
углом .
Рис. 1.19
Из формул (1.15) и (1.16) следует:
а) при = 0° (поперечное сечение бруса) ; ,
т.е.
б) при = 90° (продольное сечение бруса) ;
, т.е.
в) при = 45° ; , т.е.
Значит, при одноосном растяжении максимальное нормальное напряжение
возникает в поперечных сечениях бруса; максимальное касательное
напряжение возникает в сечениях, наклоненных к оси бруса под
углом 45°.
Кроме того, из равенства (1.16) следует, что переход от произвольной площадки с
наклоном к площадке с наклоном +90° (рис. 1.19) никак не отражается на
абсолютном значении касательньих напряжений. Действительно, если
.
Следовательно
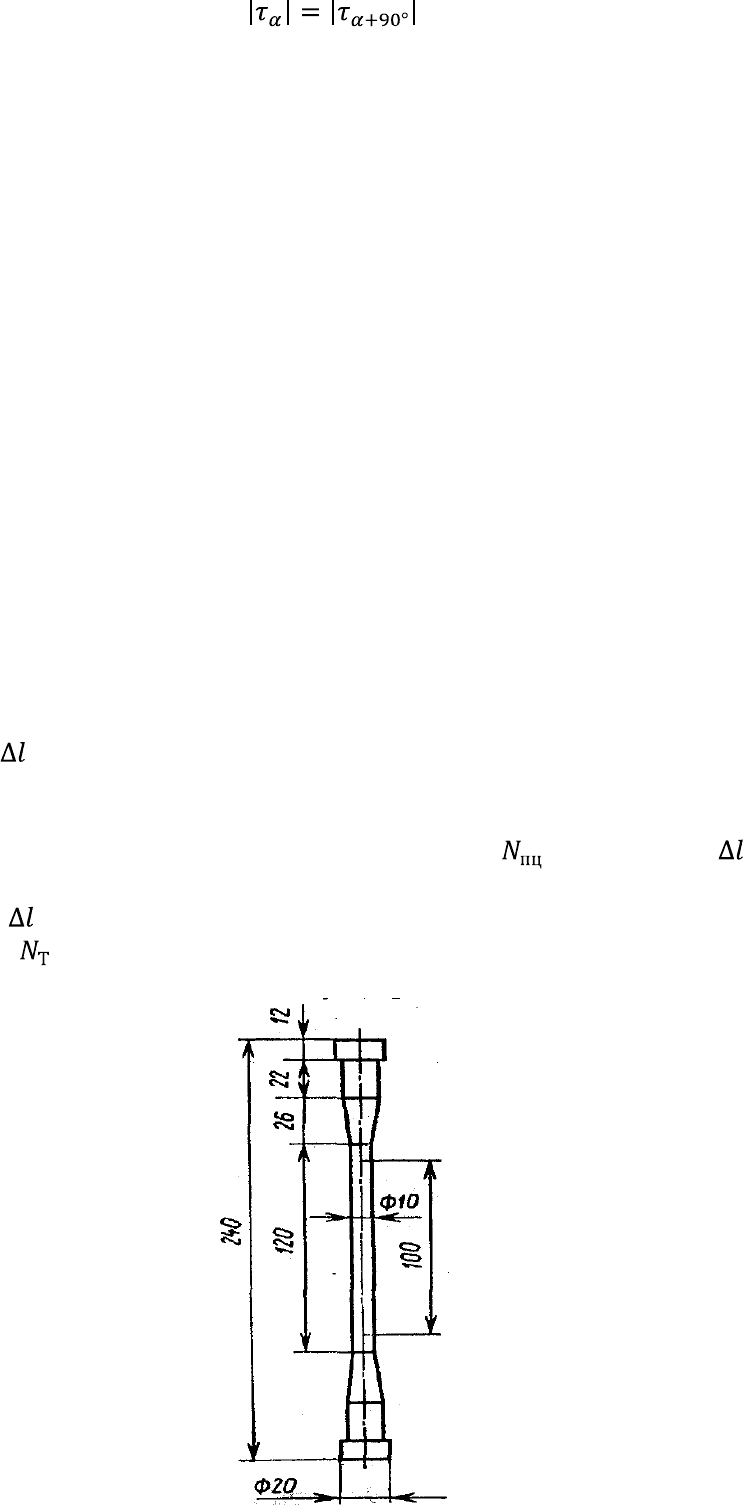
.
Это равенство выражает закон парности касательных напряжений: касательные
напряжения, возникающие в двух взаимно перпендикулярных площадках, равны
друг другу по модулю и направлены либо от ребра, либо к ребру, образуемому
площадками.
§ 1.9. Статические испытания материалов. Основные механические
характеристики.
При выборе материала для какого-либо элемента конструкции в последующих
расчетах необходимо знать механические свойства материала, определяющие его
прочность, упругость, твердость и пластичность. Необходимые сведения о различных
механических свойствах материалов получают экспериментально в процессе
механических испытаний на растяжение, сжатие, срез, кручение и изгиб.
Самыми распространенными являются испытания на растяжение. Для них из
испытуемого материала изготовляют стандартные образцы, один из которых
изображен на рис. 1.20. Образцы испытывают на разрывных машинах, где осевые
нагрузки растягивают их и доводят до разрыва. Поведение образцов по мере роста
нагрузки фиксируется на бумажной ленте с помощью особого записывающего
устройства.
На рис. 1.21 изображена примерная диаграмма, записанная при испытании образца
из низкоуглеродистой стали. По оси абсцисс в определенном масштабе зафиксирован
рост удлинения образца, а по оси ординат — возникающая в его поперечном
сечении нормальная сила N, численно равная осевой нагрузке F, прилагаемой к
образцу. Характерные точки на диаграмме отмечены цифрами 1, 2, 3 и 4.
В начале испытания (до отметки 1 с ординатой ) удлинение растет
пропорционально силѐ N, тем самым подтверждается справедливость закона Гука.
Далее удлинение возрастает непропорционально силе N. При некотором значении
нормальной силы (отметка 2) образец удлиняется без увеличения нагрузки. Это
явление называется текучестью металла.
Рис. 1.20
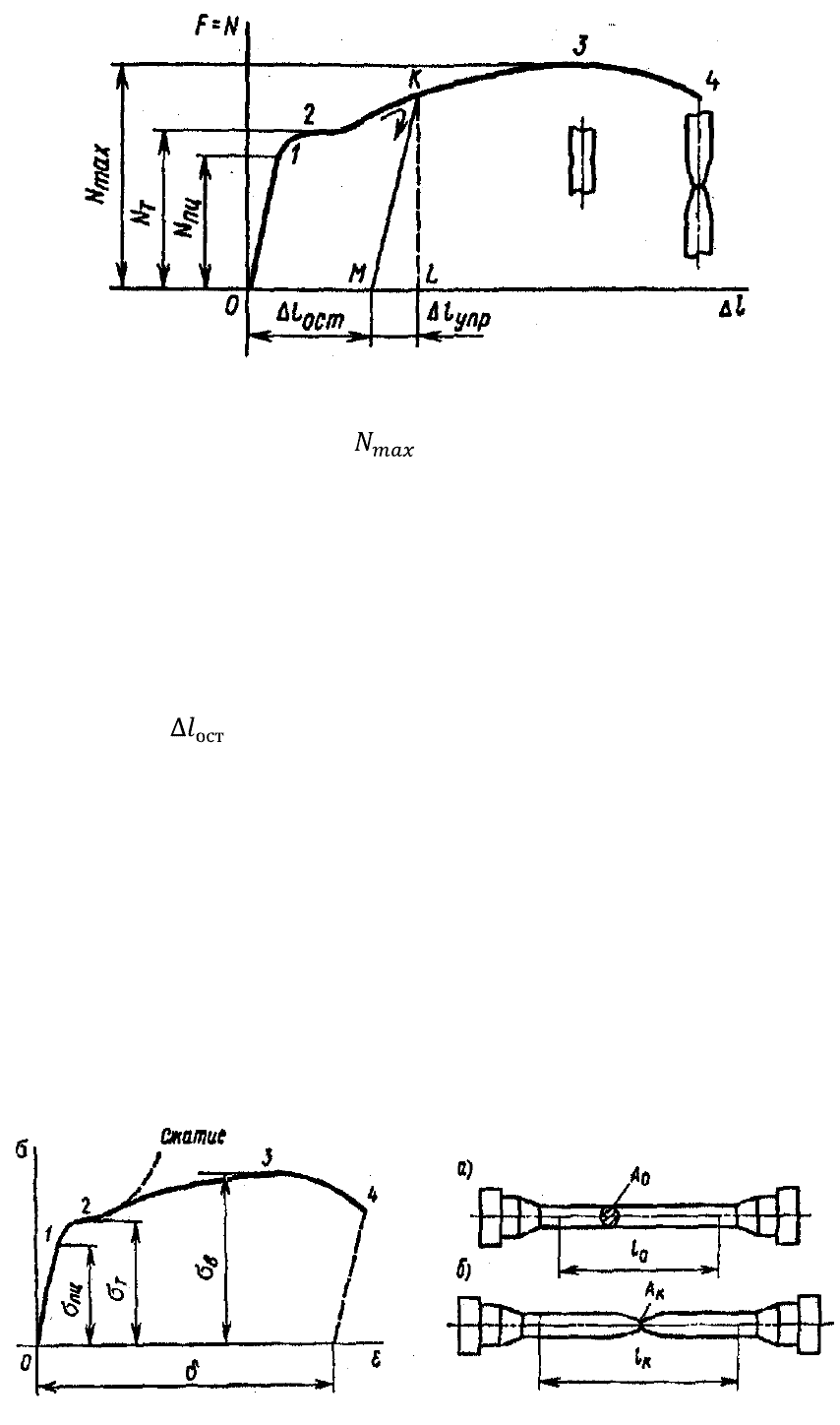
Рис. 1.21
По окончании стадии текучести материал образца снова начинает сопротивляться
нагрузке до отметки 3 с ординатой , после которой наблюдается снижение
сопротивляемости образца нагрузке. Это обстоятельство объясняется тем, что на
образце начинает появляться местное сужение (шейха) и в дальнейшем диаграмма
фиксирует уже растяжение не всего образца, а только его участка в зоне
образовавшейся шейки. Момент окончательного разрушения образца отмечен цифрой
4.
Если после перехода через стадию текучести, например в момент, отмеченный на
диаграмме точкой K (рис. 1.21), образец разгрузить, то процесс разгрузки изобразится
отрезком KM, параллельным отрезку в начале испытания. Как видим, после разгрузки
остаточное удлинение не стало равным удлинению образца, выраженному
отрезком OL, а уменьшилось на значение упругого удлинения. Теперь если этот же
образец подвергнуть повторному нагружению, то окажется, что линия нагрузки
совпадет с линией МК, т. е. часть диаграммы левее этой линии не повторится.
Следовательно, после предварительной вытяжки образца за стадию текучести его
материал способен воспринимать большие нагрузки без остаточных деформаций.
Явление повышения упругих свойств материала в результате предварительной
вытяжки выше предела текучести называется наклепом.
Нормальные силы, возникающие в образце, и его удлинения не могут служить
объективными критериями для оценки свойств материала, так как зависят от
абсолютных размеров самого образца.
Чтобы получить механические характеристики материала, диаграмму, снятую при
испытании образца,
Рис. 1.22 Рис. 1.23
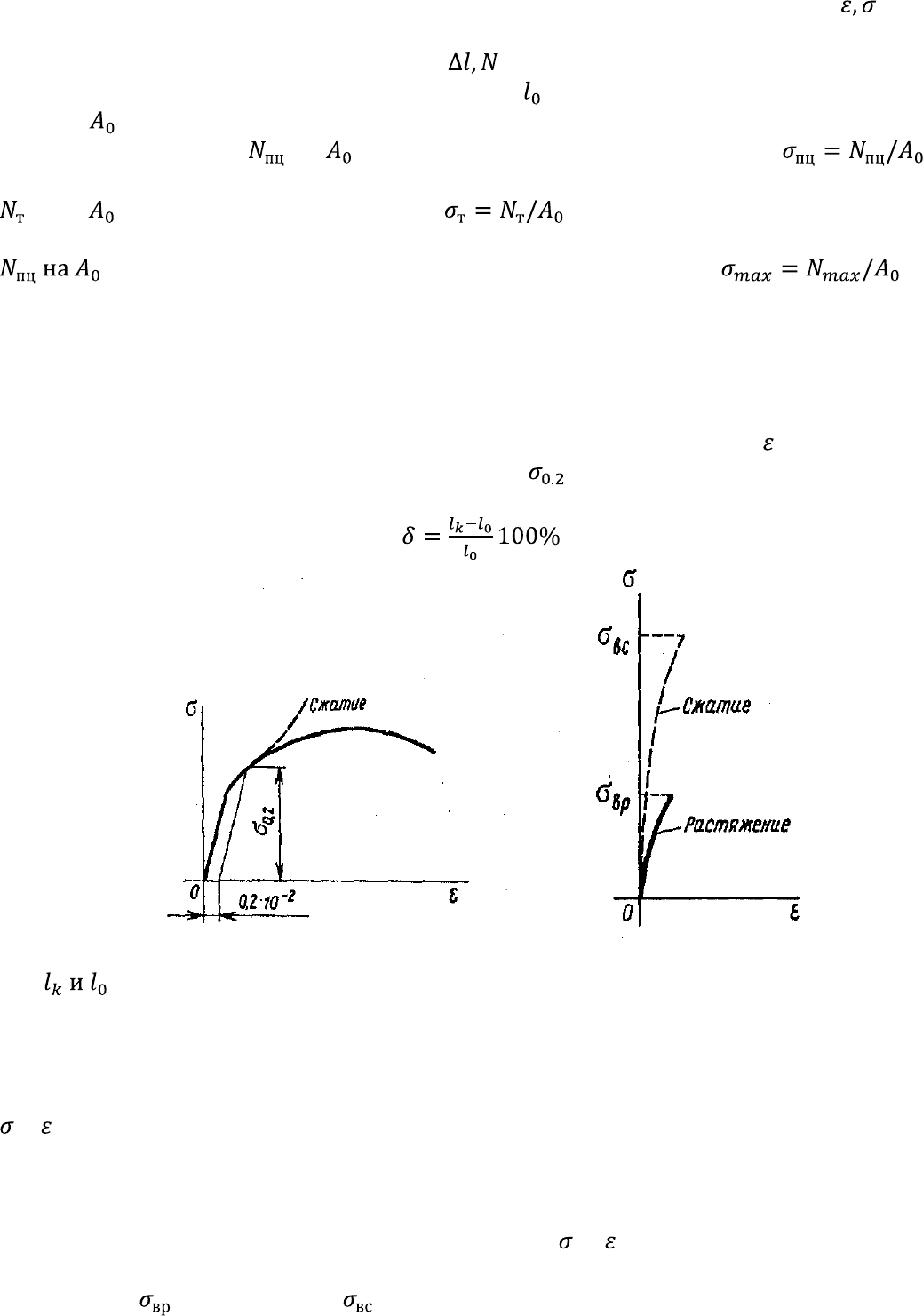
нужно перестроить в условную диаграмму растяжения в координатах ( ), не
зависящих от абсолютных размеров образца (рис. 1.22). Для этого все абсциссы и
ординаты на диаграмме в координатах ( ) (см. рис. 1.21) необходимо разделить
соответственно на начальную расчетную длину и начальную площадь поперечного
сечения образца (рис. 1.23, а).
Разделив ординату на , получим предел пропорциональности ,
т. е. наибольшее напряжение, до которого справедлив закон Гука; разделив ординату
на , получим предел текучести , т. е. напряжение, при котором
происходит рост пластической деформации при неизменной нагрузке; разделив
, получим предел прочности (временное сопротивление) , т.
е. условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой
образцом до разрушения.
При испытании некоторых пластических материалов (среднеуглеродистая сталь,
медь, алюминий) на диаграмме растяжения не образуется ясно выраженной стадии
текучести (рис. 1.24). для таких материалов вводится условный предел текучести,
равный напряжению, при котором продольная деформация образца = 0,002, т. е.
0,2%, Условный предел текучести обозначается . Пластичные свойства материала
оцениваются остаточной деформацией при разрыве
,
Рис. 1.24 Рис. 1.25
где — длины расчетной части образца после разрыва и до начала испытания
(см. рис. 1.23, а, б).
При испытании на сжатие пластические материалы до предела текучести ведут
себя так же, как и при растяжении, но далее пластическая деформация растет
медленнее. Образец постепенно сплющивается. На рис. 1.22 и 1.24 зависимость между
и при сжатии образцов показана штриховой линией.
При испытании хрупких материалов (например, чугунных образцов) установлено,
что они способны выдерживать гораздо большие нагрузки при сжатии, чем при
растяжении. Вид диаграмм при испытании чугунных образцов показан на рис. 1.25.
Сплошной линией изображена зависимость между и при растяжении, штриховой
линией — при сжатии. По этим диаграммам определяют пределы прочности при
растяжении ( ) и при сжатии ( ). Для хрупких материалов
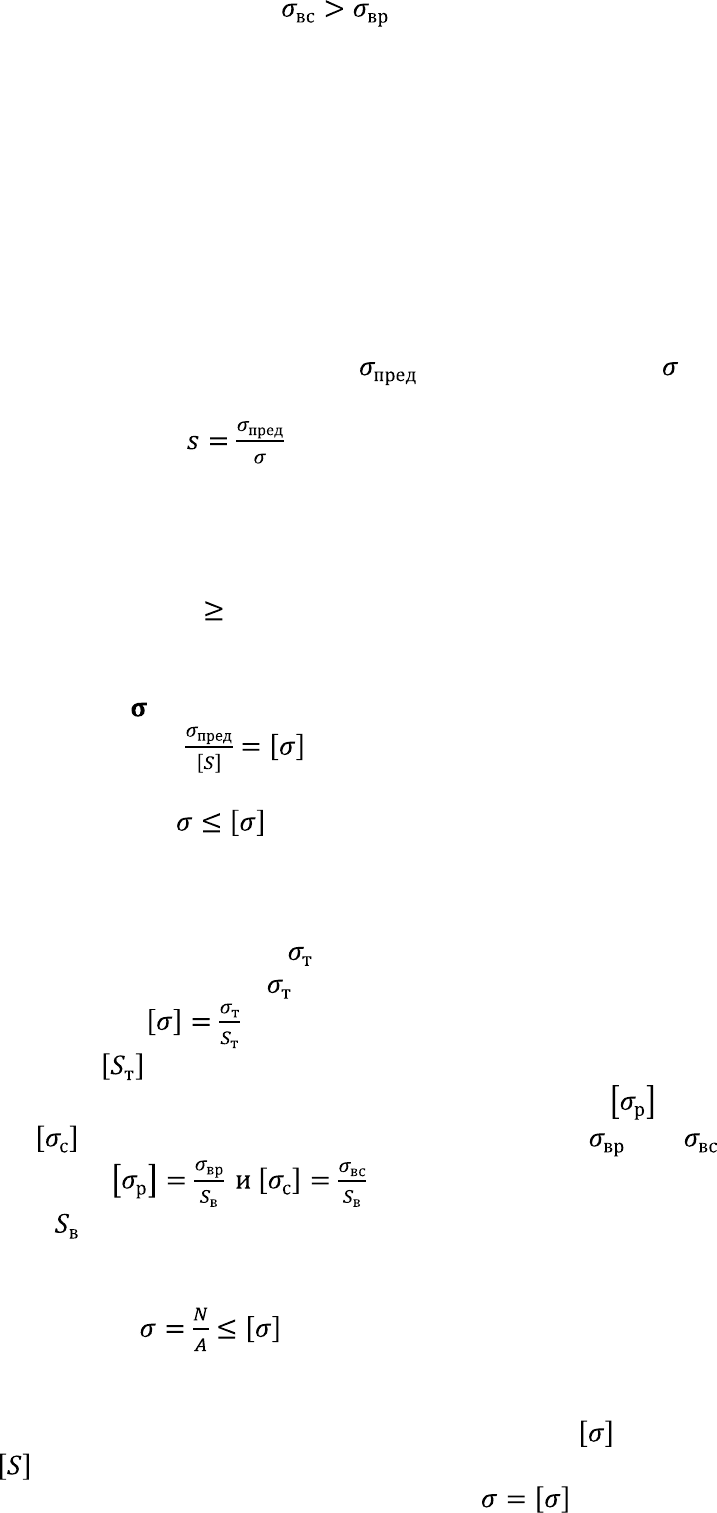
.
Аналогичная диаграмма, но с более высокими ординатами получается для
закаленных сталей.
§ 1.10. Расчеты на прочность
При проектировании элемента конструкции необходимо определить размеры,
обеспечивающие его безопасную работу при заданных нагрузках. для успешного
решения этой задачи необходимо исходить из того, чтобы наибольшее расчетное
напряжение в поперечном сечении элемента конструкции, возникшее при заданной
нагрузке, было меньше того предельного напряжения, при котором возникает
опасность появления пластической деформации или опасность разрушения.
Отношение предельного напряжения к расчетному называется
коэффициентом запаса прочности s:
. (1.17)
При расчете элемента конструкции коэффициент запаса прочности задается
заранее и называется нормативным или требуемым и обозначается [s].
Прочность элемента конструкции обеспечивается, если действительный
коэффициент запаса прочности не ниже требуемого т. е.
S [S]. (1.18)
Неравенство (1.18) выражает условие прочности элемента конструкции.
Разделив предельное напряжение на нормативный коэффициент запаса, получим
допускаемое напряжение [ ]:
. (1.19)
Тогда условие прочности можно выразить неравенством
. (1.20)
т. е. прочность элемента конструкции обеспечивается, если наибольшее
напряжение, возникающее в нем, не превышает допускаемого.
Для пластических материалов, как при растяжении, так и при сжатии предельным
напряжением является предел текучести . Поэтому для них допускаемое напряжение
получают исходя из предела текучести :
, (1.21)
причем в этом случае = 1 ,4...2.
Для хрупких материалов допускаемое напряжение растяжения и допускаемое
напряжение сжатия получают исходя из пределов прочности или .
. (1.22)
в этом случае [ ] = 2,5...5, а иногда и выше. Условие прочности (1.20)
применительно к расчетам на прочность при растяжеыии (сжатии) записывается в
таком виде:
. (1.23)
Исходя из этого условия, производят три вида расчетов.
Проектировочный расчет. При этом расчете известны нагрузки, действующие на
брус, заданы или выбраны материал, допускаемое напряжение или нормативный
запас прочности . Размеры поперечного сечения бруса, обеспечивающие требуемую
прочность, определяем следующим образом: полагая , из уравнения (1.23)
получаем расчетную формулу
