Angermann L. (ed.). Numerical Simulations - Applications, Examples and Theory
Подождите немного. Документ загружается.


Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
13
4.2.5 Discretization of the trapped holes’s number equation
In order to simplify the notations all the cross section terms are divided by the factor
|
e
|
.
Proposition 4.1 The finite volume discretization of Eq.(38) over control volume Ω
i
leads to the
discrete equation
n
hp
k+1
i
− n
hp
k
i
Δt
= σ
ph
N
ph
− n
hp
k+1
i
j
T
h
k+1
i
− σ
ae
. n
hp
k+1
i
. j
T
e
k+1
i
. (52)
which has a unique solution given by
n
hp
k+1
i
=
n
hp
k
i
+ Δt.σ
ph
.N
ph
. j
T
h
k+1
i
1 + Δt.σ
ph
j
T
h
k+1
i
+ Δt.σ
ae
j
T
e
k+1
i
(53)
for which the discrete maximum principle holds
0
≤ n
hp
k
i
≤ N
ph
. (54)
Moreover thanks to the fixed point technique, we have the following nonlinear iteration
n
hp
k+1,p+1
i
=
n
hp
k
i
+ Δt.σ
ph
.N
ph
. j
T
h
k+1,p
i
1 + Δt.σ
ph
j
T
h
k+1,p
i
+ Δt.σ
ae
j
T
e
k+1,p
i
(55)
Let us construct the finite volume discretization. We integrate Eq.(??) over control volume
Ω
i
× [t
k
,t
k+1
] to obtain
Ω
i
n
hp
(z,t
k+1
) − n
hp
(z,t
k
)
dz (56)
=
t
k+1
t
k
Ω
i
σ
ph
N
ph
− n
hp
(
z, t
)
.j
T
h
(
z, t
)
−
σ
ae
.n
hp
(
z, t
)
.j
T
e
(
z, t
)
dt
A cell-centered approximation is used for n
hp
,then
Ω
i
n
hp
(z)
k+1
− n
hp
(z)
k
dz
= h
i
n
hp
k+1
i
− n
hp
k
i
. (57)
But a vertex-centered approximation is used for j
e±,h±
(z,t), so we apply a first order
approximation to the integral, i.e. we evaluate the integrand,which is a fonction of j
e±,h±
(z,t)
at z = z
i
while n
hp
(z,t) is a constant over Ω
i
× [t
k
,t
k+1
] and equal to n
hp
k+1
i
, to obtain
t
k+1
t
k
Ω
i
σ
ph
N
ph
− n
hp
(
z, t
)
.j
T
h
(
z, t
)
−
σ
ae
.n
hp
(
z, t
)
.j
T
e
(
z, t
)
dt
= h
i
Δt
σ
ph
N
ph
− n
hp
k+1
i
j
T
h
k+1
i
− σ
ae
. n
hp
k+1
i
. j
T
e
k+1
i
. (58)
We now prove by induction that the discrete maximum principle holds.
101
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method

14 Numerical Simulations, Applications, Examples and Theory
–Fork = 0, thanks to the initial condition, we have ∀i ∈
[
1, I
]
, n
hp
0
i
= 0 ∈
0, N
ph
,sothe
condition is fulfilled.
– For a given time index k, let us assume that n
hp
k
i
∈
0, N
ph
. Computation of n
hp
k+1
i
is
given by expression
n
hp
k+1
i
=
n
hp
k
i
+ Δt.σ
ph
N
ph
. j
T
h
k+1
i
1 + Δt.σ
ph
. j
T
h
k+1
i
+ Δt.σ
ae
. j
T
e
k+1
i
= α. n
hp
k
i
+ β.N
ph
(59)
where
1
+ Δt.σ
ph
. j
T
h
k+1
i
+ Δt.σ
ae
. j
T
e
k+1
i
α
= 1, (60)
1
+ Δt.σ
ph
. j
T
h
k+1
i
+ Δt.σ
ae
. j
T
e
k+1
i
β
= Δt.σ
ph
. j
T
h
k+1
i
. (61)
but α
≥ 0, β ≥ 0, α + β ≤ 1, hence 0 ≤ n
hp
k+1
i
≤ max
n
hp
k
i
, N
ph
= N
ph
.Sothediscrete
maximum principle is verified for n
hp
k+1
i
.
A similar result can be stated and proved for the discrete approximation of trapped electron’s
equation.
4.3 Numerical simulations
4.3.1 Analysis of the influence of
E
kin
In this subsection we investigate the sensibility of Q
p
(t) and ees(t) with respect to the energy
of the primary electrons. We assume that N
pe
, N
ph
and cross sections σ
ae,h
are fixed.
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.2
2.4
0 0.0005 0.001 0.0015 0.002
see yield
t[s]
1kev
3kev
5kev
7kev
10kev
Fig. 6. Evolution of the secondary electron emission ratio as a function of time t, for various
values of E
kin
.
The behaviour of see with respect to E
kin
is presented in Fig.6 and shows that for small values
of E
kin
the ratio starts from a value greater than one and decreases down to one very quickly.
On the other hand for values of E
kin
greater than 5 kev, the ratio starts below one, and strictly
increases to the asymptotic value of one.
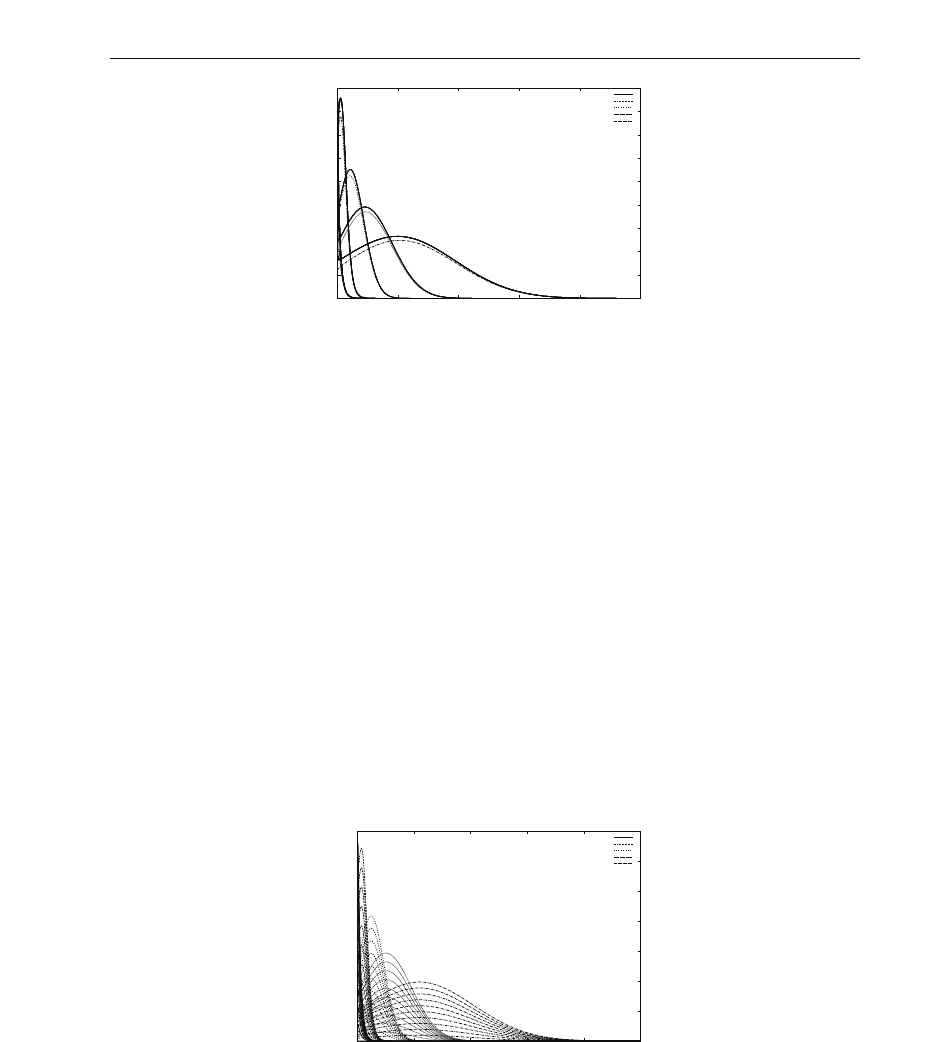
Spatial profiles of electron current j
e−,+
(
z, t
)
and holes currents j
h−,+
(
z, t
)
are similar in shape
and amplitude, hence we only repesented in Fig.7. j
e−
profiles. It is worth mentioning that
102
Numerical Simulations - Applications, Examples and Theory
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
15
0
1
2
3
4
5
6
7
8
9
0 5e-007 1e-006 1.5e-006 2e-006 2.5e-006
jem(z)
z [m]
1kev
3kev
5kev
7kev
10kev
Fig. 7. Spatial distribution of electron current j
e−
(z,t) over domain
[
0, L
]
, for various values
of E
kin
at times k × 200.10
−6
,with0≤ k ≤ 10.
increasing E
kin
induces that the maximum of j
c
(
z, t
)
decreases and the profiles are diffused
pushed towards z
= L. This result is correlated with the shape of the source term S
e
(
z
)
which
varies accordingly when E
kin
increases.
Trapped holes n
hp
(z,t) andtrappedelectronsn
ep
(z,t) are respectively represented in Fig.9
and Fig.8. The maximum of n
ep
(z,t) is smaller than the maximum of n
hp
(z,t) for each value
of E
kin
and always decreases when E
kin
increases while the spatial profiles are smeared out.
The variation of log
(ees(Qp)) is represented in Fig.10 and shows a significant difference
depending on the value of E
kin
.WhenE
kin
is below 5 kev, a strictly superlinear smooth
decreasing profile is observed. On the other hand when E
kin
is higher than 5 kev, the profiles
have a high curvature.
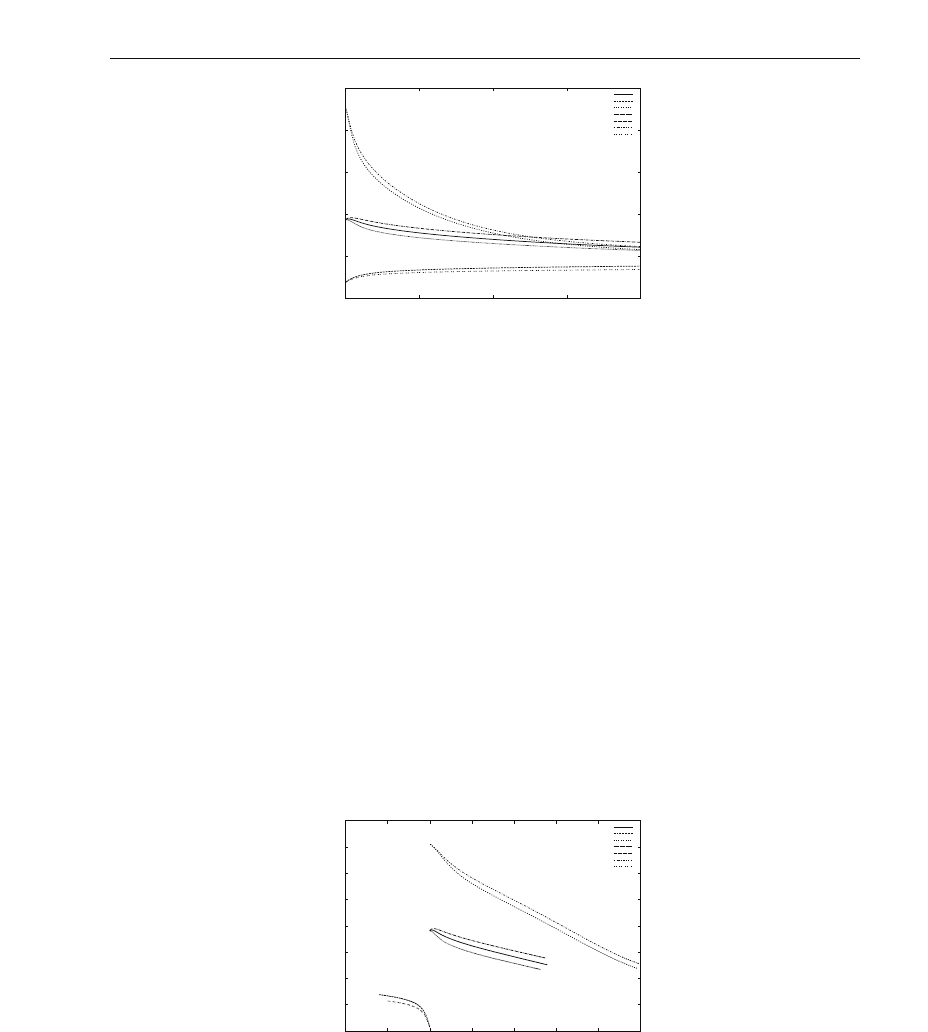
Fig.11 is an enlarged representation of electric field E
(z,t). Three different domains can be
observed for each value of E
kin
and for each time step. A) a thin boundary layer located near
the interface z
= 0wheretheE(z,t) is stiff, B) a central part where E(z,t) is oscillating and a
third part near the interface z
= L where E(z,t) is flat.
4.3.2 Analysis of the influence of the va lue of N
pe
and N
ph
In this subsection we assume that the kinetic energy of the incident electron beam is constant
and given the value of 4 kev, and study the influence of N
pe
,andN
ph
on the variation of sse(t)
and Q
p
(t). The trend observed in the numerical simulations appears independent of E
kin
.
0
100000
200000
300000
400000
500000
600000
700000
0 5e-007 1e-006 1.5e-006 2e-006 2.5e-006
nep(z)
z [m]
1kev
3kev
5kev
7kev
10kev
Fig. 8. Spatial distribution of trapped electrons n
ep
(z,t) over domain
[
0, L
]
, for various values
of E
kin
at times k × 200.10
−6
,with0≤ k ≤ 10.
103
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method

16 Numerical Simulations, Applications, Examples and Theory
0
100000
200000
300000
400000
500000
600000
700000
800000
900000
0 5e-007 1e-006 1.5e-006 2e-006 2.5e-006
nhp(z)
z [m]
1kev
3kev
5kev
7kev
10kev
Fig. 9. Spatial distribution of trapped holes n
hp
(z,t) over domain
[
0, L
]
, for various values of
E
kin
at times k × 200.10
−6
,with0≤ k ≤ 10.
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-0.0004 -0.0002 0 0.0002 0.0004 0.0006 0.0008 0.001 0.0012
loog(ees)
qp
1kev
3kev
5kev
7kev
10kev
Fig. 10. Evolution of log(ees) as function Q
p
for various values of E
kin
.
-1.5e+006
-1e+006
-500000
0
500000
1e+006
1.5e+006
0 5e-007 1e-006 1.5e-006 2e-006 2.5e-006
E(z)
z [m]
1kev
3kev
5kev
7kev
10kev
Fig. 11. Spatial distribution of electric field E(z, t) over domain
[
0, L
]
, for various values of
E
kin
at times k × 200.10
−6
,with0≤ k ≤ 10.
104
Numerical Simulations - Applications, Examples and Theory
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
17
0.5
1
1.5
2
2.5
3
0 0.0005 0.001 0.0015 0.002
ees(t)
t[s]
Npe=Nph=10^22
2*Npe
0.5*Npe
2*Nph
0.5*Nph
0.5*Npe,0.5*Nph
2*Npe,2*Nph
Fig. 12. Sensibility of the temporal evolution of see(t) when both values of N
pe
and N
ph
are
varied simultaneously or independently for E=4keV.
As seen on Fig.12, reducing in/dependently N
pe
and N
ph
leads to a significant increase of the
secondary electron emission ratio well above 1. On the other hand reducing in/dependently
N
pe
and N
ph
leads to a significant decrease of the total trapped charge Q
p
(t).
The analysis of the evolution of log
(ees(Q
p
(t))) represented in Fig.13 shows that setting N
pe
and varying N
ph
induces that the curves are parallel, but converging to the same point where
Q
p
= 0. On the other hand, setting N
ph
and varying N
pe
above or below the initial value of
N
pe
leads to a much wider variation of see above or below 1 as seen on Fig.12.
As a conclusion, the most important parameter in these simulations appears to be N
pe
.
4.3.3 Comparison between numerical computations and experimental results
Preliminary promising results are presented in Fig.14.
5. Transient see computation by a reaction-diffusion method
In section 5, we extend the reformulation of the two-fluxes modelling presented in section
4 into a reaction-diffusion modelling. The main strength of this new approach is the ability
to be extended in two/three spatial dimensions. Moreover, it is more difficult to extend in
two/three-spatial dimensions the two-fluxes approach borrowed from the radiative transfer
(Chandrasekhar 1961), hence this new approach seems more promising.
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
-0.0004 -0.0002 0 0.0002 0.0004 0.0006 0.0008 0.001
log(ees)
qp
Npe=Nph=10^22
2*Npe
0.5*Npe
2*Nph
0.5*Nph
0.5*Npe,0.5*Nph
2*Npe,2*Nph
Fig. 13. Evolution of log(ees) as function Q
p
when both values of N
pe
and N
ph
are varied
simultaneously or independently for E=4keV.
105
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method

18 Numerical Simulations, Applications, Examples and Theory
0
0.2
0.4
0.6
0.8
1
1.2
0 0.1 0.2 0.3 0.4 0.5 0.6
log(ees(t))
qp(t)
comp:0.6kev
exp:0.6kev
comp:1.0kev
exp:1.0kev
comp:1.5kev
exp:1.5kev
Fig. 14. Comparison between experimental and computed values of secondary electron
emission yield see
(t) versus trapped charge Q
p
(t).
5.1 Mathematical Modelling
We present the modelling composed of a set of two, one dimensional reaction-diffusion
equations for electrons/holes coupled with Gauss equation for the electric field and an
equation for trapped electrons/holes evolution.
5.1.1 Governing equation for the electric field E(z, t)
The local conservation equation for the electric field E(z, t) writes
∇.E
(
z, t
)
=
ρ
(
z, t
)
ε
0
ε
r
(62)
The boundary condition at z
= 0, derived from an electrostatic analysis is written
E
(
0, t
)
= −
1
ε
0
ε
r
(
1 + ε
r
)
L
0
ρ
(
z, t
)
dz (63)
5.1.2 Governing equation for charge density ρ(z, t)
We define the overall current flux j
T
(
z, t
)
=
j
e
(
z, t
)
−
j
h
(
z, t
)
−
j
0
j
prim
(
z
)
. The conservation
law expressing the evolution of charge density ρ
(z,t) is written
∂ρ
(
z, t
)
∂t
+ ∇.j
T
(
z, t
)
=
0 (64)
with initial condition ρ
(
z,0
)
=
0 expressing the lack of charge.
5.1.3 Governing equations for the number of free charges
(
n
c
(
z, t
))
c∈C
and current fluxes
j
c
(z,t)
For charge c, the number of trapped charge, either electrons or holes, n
c
(
z, t
)
is based on the
following balance equation
∂n
c
∂t
(
z, t
)
+ ∇
.j
c
(
z, t
)
=
2S
c
(
z
)
−
σ
abs
c
v
n
c
(
z, t
)
(65)
The current flux for charge c j
c
(
z, t
)
is related to the number of free charges n
c
(
z, t
)
thanks to
the equation
j
c
(
z, t
)
= −
D
c
∇n
c
(
z, t
)
+
n
c
(
z, t
)
μ
c
s
c
E
(
z, t
)
. (66)
106
Numerical Simulations - Applications, Examples and Theory
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
19
For a given charge c ∈ C,itssigns
c
is set to be +1 for the holes and −1 for the electrons and
its mobility is represented by μ
c
≥ 0. The diffusion coefficient D
c
is defined by D
c
=
v
c
σ
trans
c
,
where σ
trans
c
= σ
abs
c
+ 2σ
di f f
c
. Hence the partial differential equation related to the evolution of
n
c
(
z, t
)
is rewritten
∂n
c
∂t
(
z, t
)
+ ∇
.
(
−
D
c
∇n
c
(
z, t
)
+
n
c
(
z, t
)
μ
c
s
c
E
(
z, t
))
=
2S
c
(
z
)
−
σ
abs
c
v
n
c
(
z, t
)
(67)
It is a linear reaction-convection-diffusion equation of parabolic type for unknown n
c
(z,t),
expressed in conservation form. Two boundary conditions at interfaces z
= 0andz = L must
be given in order for the problem to be well-posed. Following the discussion presented in
Section 3, we use the following conditions that depend on the charge c.
–atz
= 0
−D
e
∂n
e
(
z, t
)
∂z
− μ
e
n
e
(
z, t
)
E
(
z, t
)
z=0
= −
κ
2 − κ
v
e
n
e
(
0, t
)
,
−D
h
∂n
h
(
z, t
)
∂z
+ μ
h
n
h
(
z, t
)
E
(
z, t
)
z=0
= 0.
–atz
= L
−D
e
∂n
e
(
z, t
)
∂z
− μ
e
n
e
(
z, t
)
E
(
z, t
)
z=L
= v
e
n
e
(
L, t
)
,
−D
h
∂n
h
(
z, t
)
∂z
+ μ
h
n
h
(
z, t
)
E
(
z, t
)
z=L
= v
h
n
h
(
L, t
)
5.2 Numerical scheme
We discuss an implicit finite-volume scheme, on a non uniform spatial grid and focus
the analysis on the discrete maximum principle fulfilled by the numerical scheme for
this linear reaction-convection-diffusion equation. The number of free charges n
c
(z,t) is
positive, a discretization of the equation must give positive values. We know that for
convection diffusion equation, upwind schemes induce artificial numerical diffusion that can
be monitored thanks to the local Peclet number. Moreover a boundary layer characterizes the
modelling. A discrete maximum principle must be verified for the discretization of
∇.
(
n
c
(z,t)μ
c
s
c
E(z, t)
)
(68)
To this end, the finite volume discrete approximation is given by the following expression,
where to simplify the notations, we have defined v
c
(z,t)=μ
c
s
c
E(z, t),
Ω
i
∇.
(
n
c
(z,t)v
c
(z,t)
)
= n
k+1
i
+
1
2
v
k+1
i
+
1
2
− n
k+1
i
−
1
2
v
k+1
i
−
1
2
. (69)
Taking into account the signs of v
i+
1
2
leads to
–ifv
k+1
i
+
1
2
≥ 0, then n
k+1
i
+
1
2
= n
k+1
i
, while if v
k+1
i
+
1
2
≤ 0, then n
k+1
i
+
1
2
= n
k+1
i
+1
.
A discrete maximum principle is then easily established following the method described in
section 3. Work is in progress to analyse the numerical results.
107
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method

20 Numerical Simulations, Applications, Examples and Theory
6. Numerical software sirena
We describe briefly the architecture of our numerical software sirena. It is a toolbox for the
numerical solution either by a two-fluxes method or by a reaction-diffusion method of the
see yield. It is written in C language and consists of distinct modules that compute, the
initial mesh either uniform or geometrically refined near z
= 0, and solve the electric field
equation, trapped charge density equation, etc . Several specialized data structures are used.
The visualization is possible thanks to scripts written for gnuplot software but also in VTK
format for the animated visualization of time-dependent quantities. It has been compiled
under windows xp with a free C compiler, DEV-CPP while under linux with gnu gcc. A
typical run with an adequate refined mesh requires less than a minute on a standard laptop.
7. Conclusions and perspectives
In this book chapter, we have presented a modelling for the computation of the initial
and transient true see yield following a traditional two-fluxes approach. We have stressed
the discrete maximum principle property of the conservative finite-volume numerical
discretization presented in this chapter. A new asymptotic expression for the initial true see
yield was presented and discussed.
A new approach, in this field, based on a reaction-diffusion modelling was presented for
both initial and transient computation of true see yield. As in the two-fluxes approach, we
have analyzed the discrete maximum principle properties of the finite-volume discretization
scheme and provided some numerical simulations.
Finally, a numerical software sirena freely available upon request was presented.
In the future, We plan to extend this reaction-diffusion approach in two-spatial dimensions in
order to perform numerical simulations of charge trapping inside the material for focalized
electron beam, because in this case, lateral and longitudinal distributions of electrons/holes
are important. This requires the knowledge for the creation of free electron/holes inside
the sample. There appears to be no expression for such term in the litterature, which
has a pear-like shape according to some monte carlo computations. We plan to use such
computations and curve-fitting in order to obtain a law that will be plugged into the 2D
version of sirena.
8. References
Aoufi, A. & Damamme, G. (2009). Numerical computation of secondary electron emission
yield by a two-fluxes method, Proceedings of ICNAAM 2009, AIP, Rethymno - Crete.
Aoufi, A. & Damamme, G. (n.d.). 1d numerical simulation of charge trapping in an insulator
submitted to an electron beam irradiation
part i: Computation of the initial secondary electron emission yield, Applied
Mathematical Modelling . www.elsevier.org.
Fitting, H.-J. (1974). Phys. Stat. Sol. A. 26: 525–535.
G. Damamme, C. L. & Reggi, A. D. (1997). IEEE Trans.Dielec.Elect.Insul Vol. 5(No. 4): 558–584.
H.-J. Fitting, H. G. & Wild, W. (1977). Physical Status Solid (a) (43): 185–190.
I.A.Glavatskikh, V. S. K. & Fitting, H.-J. (2001). ’self-consistent electrical charging of insulating
layers and metal-insulator-semiconductor structures’, J. Appl. Phys (89): 440–448.
Levy, L. (2002). Metal Charging, Cepadues Edition.
108
Numerical Simulations - Applications, Examples and Theory
5
Control of Photon Storage Time in
Photon Echoes using a Deshelving Process
Byoung S. Ham
School of Electrical Engineering, Inha University
S. Korea
1. Introduction
Since the first protocol of quantum algorithm was put forth in 1994 (Shor, 1994), quantum
information processing has been intensively studied (Nielsen & Chuang, 2000). The
quantum approach has benefits over the classical optical information processing in areas
such as prime number factorization (Shor, 1994), data searching (Grover, 1996), and high-
resolution lithography (Boto et al., 2000; Yablonovitch, 1999). Compared to conventional
cryptography based on public key cryptosystem (RSA cryptosystem) using conventional
computers, prime number factorization using quantum computers has demonstrated a
potential for a formidable attack on existing cryptographic systems. Like conventional
memory which serves in the information processing unit, such as a processing unit together
with logic gates, quantum memory is also essential to quantum information and
communications networks. For quantum communications via a classical optical channel, the
longest communication distance a quantum light can be transmitted is determined by the
sensitivity of optical detectors and a lossy classical channel such as an optical fibre. Based on
current technologies, the longest distance a single photon can propagate through an optical
fibre is about 100 km (Zbinden et al., 1998). This distance should limit applications of
quantum information especially for long-distance quantum communications. To solve the
limited photon transmission, a quantum repeater has been introduced for virtually
unlimited transmission distance (Duan et al., 2001; Jiang et al., 2007; Simon et al., 2007; Waks
et al., 2002). Quantum memory is an essential element for the entangled photon swapping in
the quantum repeaters. Because quantum repeaters swap entangled photons shared by
neighboring remote quantum nodes in a quantum network, and the quantum information
must be kept coherently through the quantum network, the minimum storage time of
quantum memory is determined by the longest transmission distance of the lossy optical
channel. For tranceatlantic quantum communications, roughly a one-second or more storage
time is required. So far, such a long photon storage has not been demonstrated, where
conventional quantum memory protocols limit the storage time to spin phase decay time at
most (≤10
-3
second).
Unlike classical memories, quantum memory must satisfy a coherent process. Since the first
observation of coherent retrieval of a stored optical pulse in a Bose Einstein condensate
using slow light (Liu et al., 2001), interest in quantum memories has increased in the last
decade (Alexander et al., 2006; Afzelius et al., 2010; Chaneliere et al., 2005. Choi et al., 2008;

Numerical Simulations - Applications, Examples and Theory
110
Ham, 1998; Ham 2009a; Ham, 2010a; Hedges et al., 2010; Hetet et al., 2008; Hosseini et al.,
2009; Julsgaard et al., 2004; Kocharovskaya et al., 2001; Kraus et al., 2006; Liu et al., 2001;
Moiseev & Kroll, 2001; Moiseev et al., 2003; Neumann et al., 2009; Nilsson & Kroll, 2005;
Sangouard et al., 2007; Turukhin et al., 2002; Van der Wal, et al., 2003). Because temporal
multimode storage capability is required for the quantum repeaters, a photon echo-type
protocol has emerged as a best candidate. Unlike a single atom-based quantum memory,
echo-type quantum memory has the advantage of using an ensemble of atoms, where a
quantum light is efficiently absorbed by many atoms. This ensemble system also provides
near perfect storage capability as well as inherent temporal multimode capability. Following
the first observation of echo-type optical memory in a spin system (Hahn, 1950), photon
echoes were intensively studied in the 1980s and 1990s for spatiotemporal ultrahigh-speed
all-optical information processing. Unlike all-optical memories, retrieval efficiency in
quantum memories must satisfy at least a two thirds level of fidelity. In this chapter photon
echo type quantum memory protocols are reviewed and compared. The chapter is
composed of the following sections. In section 2, photon echoes are reviewed as a
background of modified echo-type quantum memories. Section 3 presents the advantages
and disadvantages of several modified photon echoes for quantum memory protocols. In
Section 4, an optical locking technique is introduced for an ultralong photon storage method
that can be applied to long-distance quantum communications. Section 5 discusses a phase
matching condition for optical locking applied to different photon echo protocols, solving a
main drawback in conventional photon echoes. Section 6 presents conclusions.
2. Review of photon echoes
Like spin echoes (Hahn, 1950), photon echoes (Kurnit, et al., 1964) use optical
inhomogeneity of an atomic ensemble. Figure 1 shows numerical simulations of a two-pulse
photon echo in a two-level atomic system. The first pulse D in Fig. 1(b) interacting with a
two-level optical system excites atoms onto the excited state |2>. For a visualization
purpose of maximum coherence, the first pulse D is set at a π/2 pulse area, where the pulse
area Φ is defined by:
,dt
Φ
=Ω
∫
and Ω is the Rabi frequency. By the interaction of the first
pulse D, atomic coherence is created between states |1> and |3>. A phase relaxation-
dependent decoherence is inevitable in any optical system. Because the atoms are
inhomogeneously broadened, randomly detuned atoms from the absorption linecentre
cause a fast dephasing of sum coherence for the atomic system. Later but before each
individual atom diphases completely, the second pulse R, whose pulse area is π, interacts
with all atoms whose sum coherence is washed out, and inverts the system to rephase. The
rephasing by the second pulse R results in a time reversal process, where initial coherence
should be retrieved after the same elapse as taken with R. Here, the photon echo as a
coherent burst has nothing to do with a population transfer process but relates only to
coherent phase retrieval of all individual atoms. The retrieval efficiency degrades as a
function of time due to the optical phase decay process as well as to optical population
decay of the excited atoms. In general, the optical phase decay time in rare-earth doped
solids is ~0.1 ms, which is too short to quantum repeaters (Macfarlane & Shelby, 1987).
Another problem of the two-pulse photon echoes is the echo reabsorption by the
noninteracted (or nonabsorbed) atoms along the propagation direction, common in an
optical medium governed by Beer’s law, where the number of atoms excited by the light
