Angermann L. (ed.). Numerical Simulations - Applications, Examples and Theory
Подождите немного. Документ загружается.

Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
3
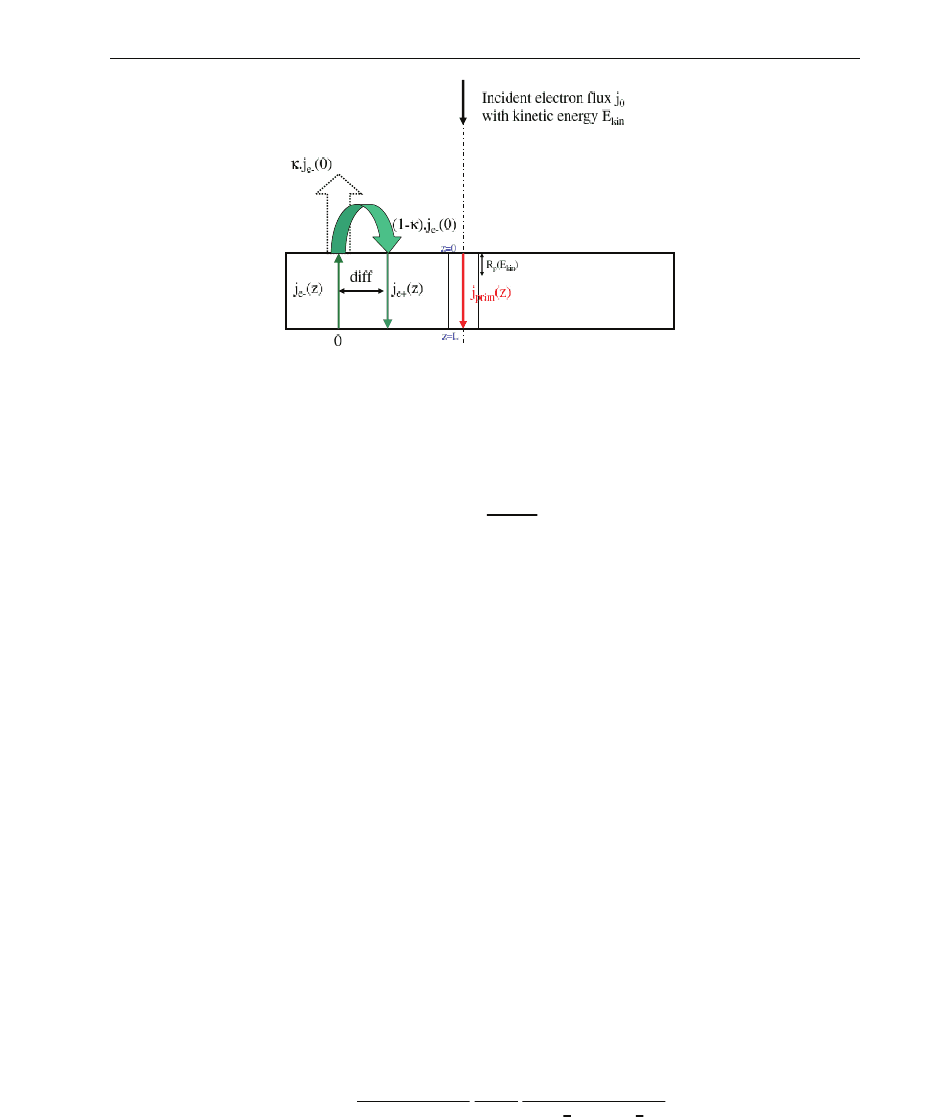
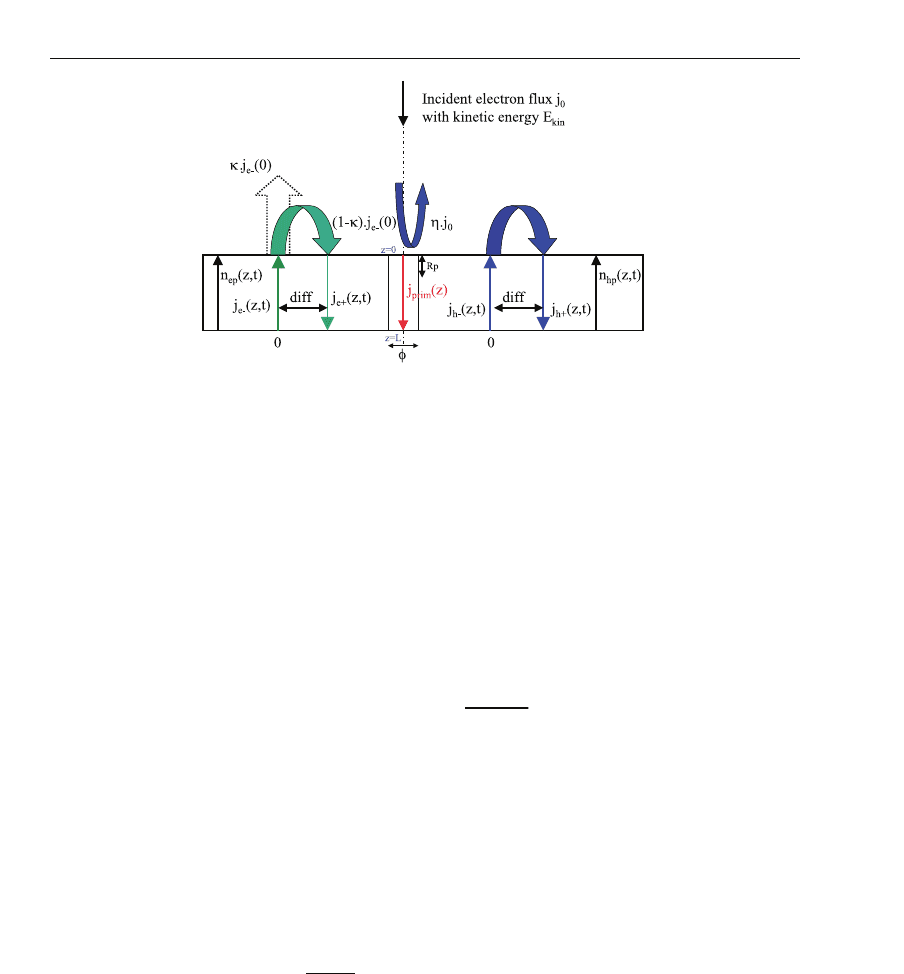
Fig. 1. Scheme of the modelling assuming that there is no backscattered electrons and where
R
p
is the penetration thickness and L is the dielectric thickness. The incident electron flux j
0
has a kinetic energy E
kin
.
mathematical modelling is used to analyse the sensibility of the true secondary electron
emission yield see
∗
defined by the expression
see
∗
= κ
j
e−
(
0
)
j
0
.(3)
with respect to the relative importance of charges absorption/diffusion inside the material,
where j
0
is the current density of primary electrons ( the backscattered electrons being
excluded ) and κ is the transmission coefficient.
2.2 Existence-uniqueness of the formal solution
The following proposition was presented in (Aoufi & Damamme, 2009)
Proposition 2.1 Denoting the constant σ
c
= σ
abs
e
+ σ
di f f
c
, and under the assumption that
[
z → S
e
(
z
)]
is continuous over Ω,then
– the problem has a unique solution
(
j
e−
(
z
)
, j
e+
(
z
))
for z ∈ Ω given by the coupled system
j
e−
(
z
)
=
L
z
S
e
(
E
kin
,u; j
0
)
+
σ
di f f
e
+
j
e+
(
u
)
e
σ
e−
(
z−u
)
du.(4)
j
e+
(
z
)
=
j
e+
(
0
)
.e
−σ
e+
z
+
z
0
S
e
(
E
kin
,u; j
0
)
+
σ
di f f
e
−
j
e−
(
u
)
e
σ
e+
(
u−z
)
du.(5)
– Moreover there exits a constant C
S
e
L
∞
(
Ω
)
, E
kin
, L,σ
abs
e
,σ
di f f
c
> 0 such that for z ∈ Ω
0
≤ j
e−,+
(
z
)
≤
j
0
.C
S
e
L
∞
(
Ω
)
, E
kin
, j
0
, L,σ
abs
e
,σ
di f f
c
2.3 Asymptotic expression for the secondary electron emission yield
Proposition 2.2 We define the transfer cross section σ
trans
e
= σ
abs
e
+ σ
di f f
e
+
+ σ
di f f
e
−
, Under the
asymption that 1
σ
abs
e
.R
p
(
E
kin
)
then
see
∗
κ
S
e
(
z = 0, E
kin
)
σ
abs
e
σ
∗
σ
trans
e
σ
∗
(1 −
κ
2
)σ
abs
e
+
κ
2
σ
∗
.(6)
91
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
4 Numerical Simulations, Applications, Examples and Theory
where
Δσ
di f f
e
= σ
di f f
e
+
− σ
di f f
e
−
,2σ
∗
= Δσ
di f f
e
+
4σ
abs
e
σ
trans
e
+
Δσ
di f f
e
2
.(7)
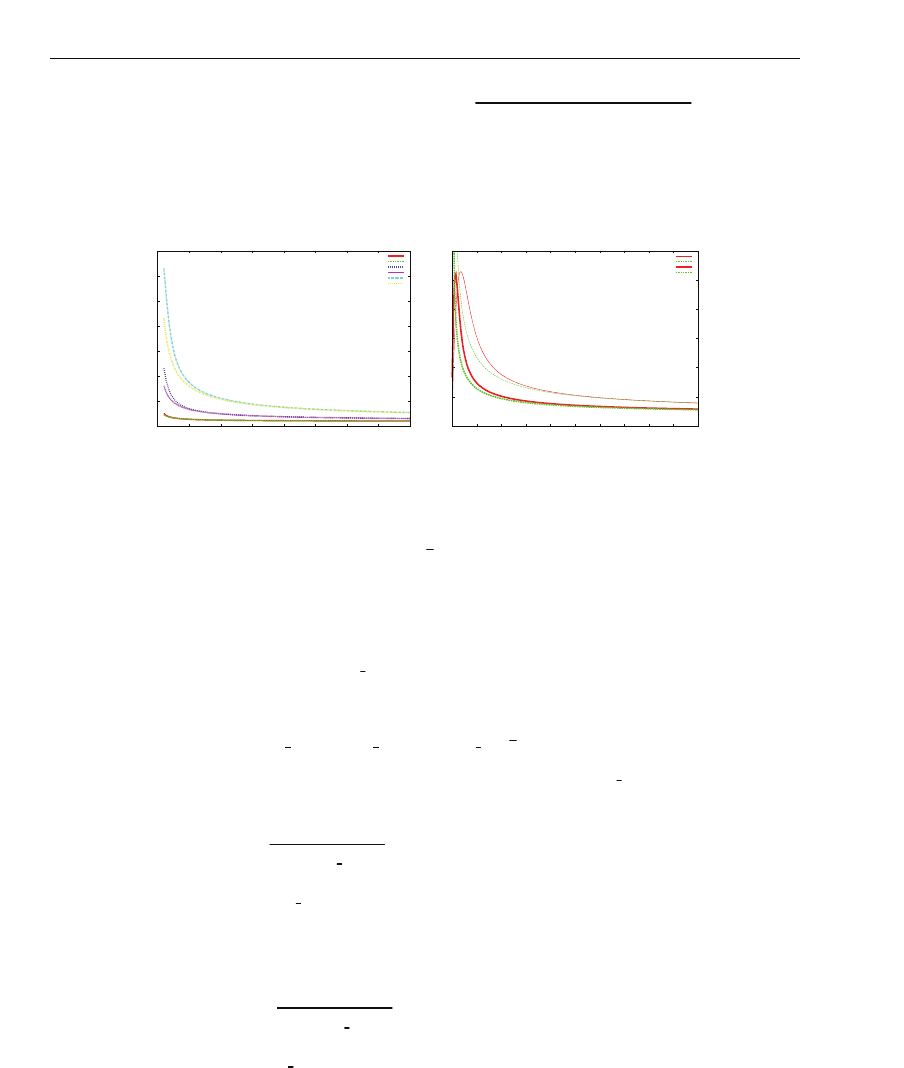
Fig.(2) represents a comparison between asymptotic formula given by Eq.(6) and computation
of see yield from Eq.(3). A good agreement is observed for high values of E
kin
.Other
computational results are given in (Aoufi & Damamme, n.d.).
0
1
2
3
4
5
6
7
0 5 10 15 20 25 30 35 40
see(E)
E [kev]
k=1/10:comp
k=1/10:asym
k=1:comp
k=1:asym
k=10:comp
k=10:asym
0
0.5
1
1.5
2
2.5
3
0 2 4 6 8 10 12 14 16 18 20
see(E)
E [kev]
nodiff:see comp
nodiff:see asym
diff:see comp
diff:see asym
Fig. 2. (a) Comparison between computed and asymptotic expression for see yield in the case
where σ
di f f
e
+
= kσ
di f f
e
and σ
di f f
e
−
= k
−1
σ
di f f
e
with k ∈
{
1/10, 1, 10
}
. (b) Comparison between
numerical values and asymptotic expression of see
∗
(
E
kin
)
as a function of E
kin
[kev] in both
cases with and without diffusion ( for σ
di f f
c
= σ
di f f
c
).
2.4 Numerical scheme
A vertex-centered conservative finite-volume discretization of the governing equation with an
adequate upwind technique is defined. The domain Ω is decomposed into a set of I control
volumes Ω
i
=
[
z
i
,z
i+1
]
with length h
i+
1
2
. The discrete unknown at grid point z
i
related to j
c
is
denoted j
c
|
i
.
Proposition 2.3 Denoting S
i+
1
2
= S
e
z
i+
1
2
,wherez
i+
1
2
=
1
2
(
z
i
+ z
i+1
)
,then
– the scheme obtained after integrating the forward linear equation over Ω
i+
1
2
is written for each cell
index i,
j
e+
|
i+1
− j
e+
|
i
h
i+
1
2
+
σ
abs
e
+ σ
di f f
e
+
+ σ
di f f
e
−
. j
e+
|
i+1
= S
i+
1
2
+ σ
di f f
e
−
j
e−
|
i+1
+ j
e+
|
i
(8)
– using a similar computation, the scheme for the backward linear equation leads to the discrete
equation
−
j
e−
|
i
− j
e−
|
i−1
h
i−
1
2
+
σ
abs
e
+ σ
di f f
e
+
+ σ
di f f
e
−
. j
e−
|
i−1
= S
i−
1
2
+ σ
di f f
e
+
j
e+
|
i−1
+ j
e−
|
i
.(9)
– The linear system with the discrete unknowns
(
j
e−
|
i
)
1≤i≤I+1
,
(
j
e+
|
i
)
1≤i≤I+1
has a unique
solution,
92
Numerical Simulations - Applications, Examples and Theory
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
5
– which verify a discrete maximum principle for a suitable constant C > 0
0
≤ j
e−,+
|
i
≤ C (10)
2.5 Numerical simulations
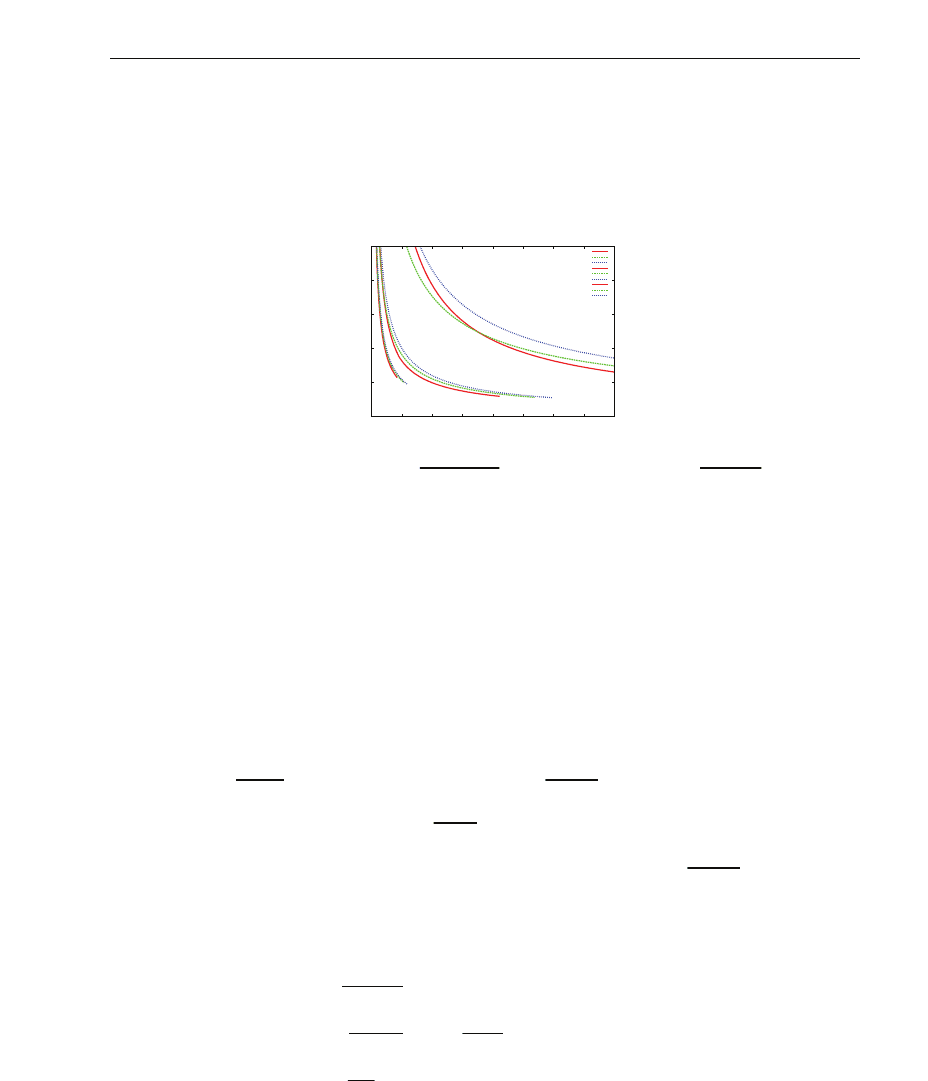
Fig.(3) shows that in a suitable normalized representation, the evolution of secondary electron
emission yield has a similar shape for different expressions of the penetration depth radius.
0
0.02
0.04
0.06
0.08
0.1
0 500 1000 1500 2000 2500 3000 3500 4000
see
*
(E
kin
)/(E
kin
)
R(E
kin
)/λ [kev
-1
]
F : λ
e
= 10
-10
m
K : λ
e
= 10
-10
m
VT : λ
e
= 10
-10
m
F : λ
e
=50 10
-10
m
K : λ
e
=50 10
-10
m
VT : λ
e
=50 10
-10
m
F : λ
e
= 10
-11
m
K : λ
e
= 10
-11
m
VT : λ
e
= 10
-11
m
Fig. 3. Reduced variables evolution of
see
∗
(
E
kin
)
E
kin
in eV
−1
as a function of
R
(
E
kin
)
λ
abs
e
for the
three penetration radius R
p
(
E
)
laws, Vyatskin and Trunev (VT), Kanaya (K) and Fitting (F)
for differents values of λ
abs
e
.
3. Initial see computation by a reaction-diffusion method
3.1 Mathematical modelling
In order to reformulate Eq.(1)-(2) into a reaction diffusion equation, let us define the number
of free electrons per unit volume n
e
(
z
)
such that for z ∈
[
0, L
]
, v
e
n
e
(
z
)
=
j
e+
(
z
)
+
j
e−
(
z
)
with
v
e
the mean absolute velocity of charge carriers and the overall transfert cross-section σ
trans
e
according to σ
trans
e
= σ
abs
e
+ 2σ
di f f
e
. After summation and substraction of Eq(1)-(2), and using
the definition of j
e
(
z
)
and n
e
(
z
)
one obtain that
dj
e
(
z
)
dz
= 2S
e
(
z
)
− <
σ
abs
e
v
e
> n
e
(
z
)
, v
e
dn
e
(
z
)
dz
= −j
e
(
z
)
σ
trans
e
. (11)
Defining the diffusion coefficient D
e
=
v
e
σ
trans
e
with respect to the transfer equation leads to
the fact that the current flux j
e
(
z
)
follows a Fick-type law : j
e
(
z
)
= −
D
e
dn
e
(
z
)
dz
. Pluging this
expression into Eq.(3) leads to the reaction-diffusion equation with Fourier type boundary
conditions
− D
e
d
2
n
e
(
z
)
dz
2
= 2S
e
(
z
)
− <
σ
abs
e
v
e
> n
e
(
z
)
(12)
D
e
dn
e
(
0
)
dz
=
κ
2 − κ
n
e
(
0
)
v
e
, (13)
D
e
dn
e
dz
(
L
)
= −
n
e
(
L
)
v
e
(14)
93
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method

6 Numerical Simulations, Applications, Examples and Theory
The reformulation of Eq.(3) in terms of the number of trapped electrons n
e
(
z
)
is easily
obtained thanks to Eq.(11) and is such that :
see
∗
=
κ
2 − κ
n
e
(
0
)
v
e
j
0
(15)
It is worth mentioning that in the case of electron transport, the velocity v
e
can be obtained
thanks to the equation
1
2
m
e
v
2
e
= E
e
where the energy E
e
was between 1eV − 3eV, and is related
to value of the gap energy.
3.2 Numerical scheme
A cell-centered finite-volume scheme on a geometrically refined grid near interface z = 0is
used. We prove the existence and uniqueness of the discrete solution that is computed by
the inversion of a sparse tridiagonal matrix thanks to the classical Thomas algorithm -i.e.
Gauss method for tridiagonal matrices-. We prove a discrete maximum principle, thanks to
the M-matrix property of the tri-diagonal matrix.
We use a classical cell-centered finite volume approximation on computational domain Ω.A
set of non-uniformly spaced grid points
(
z
i
)
1≤i≤i+1
is given, and is such that z
1
= 0 < ··· <
z
i
< ...z
I+1
= L.Wedenotebyh
i
the length of control volume Ω
i
=[z
i
,z
i+1
] and n
i
the mean
of n
(z) over control volume Ω
i
.ThereareI + 1nodes,butI control volumes.
Proposition 3.1 The finite-volume discretization of Eq.(14) leads to the following linear system
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
b
1
c
1
.
.
.
a
i
b
i
c
i
.
.
.
a
I
b
I
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
n
1
.
.
.
n
i
.
.
.
n
I
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
2h
1
S
1
.
.
.
2h
i
S
i
.
.
.
2h
I
S
I
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
with
a
1
= 0, b
1
=
D
e
h
1
+
h
2
2
+
κ
2 − κ
v
e
+ < σ
abs
e
v
e
> h
1
, c
1
= −
D
e
h
1
+
h
2
2
, (16)
and for i
∈
[
1, I − 1
]
a
i
=
D
e
h
i
+h
i−1
2
, b
i
= −
D
e
h
i
+h
i+1
2
+
D
e
h
i
+h
i−1
2
+ < σ
abs
e
v
e
> h
i
, c
i
= −
D
e
h
i
+h
i+1
2
, (17)
and
a
I
= 0, b
I
= −
D
e
h
I
+
h
I−1
2
, c
I
=
D
e
h
I
+
h
I−1
2
+ v
e
. (18)
which has a unique positive solution.
The discretization of Eq.(14) over control volume Ω
i
leads to the following discrete equation
which is specialized if i
= 1, or 1 < i < I or i = I
94
Numerical Simulations - Applications, Examples and Theory
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
7
− D
e
n
2
− n
1
h
1
+
h
2
+
κ
2 − κ
n
1
v
e
= 2h
1
S
1
+ < σ
abs
e
v
e
> n
1
h
1
(19)
−D
e
n
i+1
− n
i
h
i
+h
i+1
2
+ D
e
n
i
− n
i−1
h
i
+h
i−1
2
= 2h
i
S
i
+ < σ
abs
e
v
e
> n
i
h
i
(20)
v
e
n
I
+ D
e
n
I
− n
I−1
h
I
+
h
I−1
2
= 2h
I
S
I
+ < σ
abs
e
v
e
> n
I
h
I
(21)
The matrix of the linear system that is used to compute
(n
i
)
1≤i≤I+1
is an M-matrix, since
• b
i
≥ 0, a
i
,c
i
≤ 0, b
i
≥
|
a
i
|
+
|
c
i
|
,
• and 2h
i
S
i
≥ 0.
we conclude that it is invertible and that the unique solution of the linear system is positive.
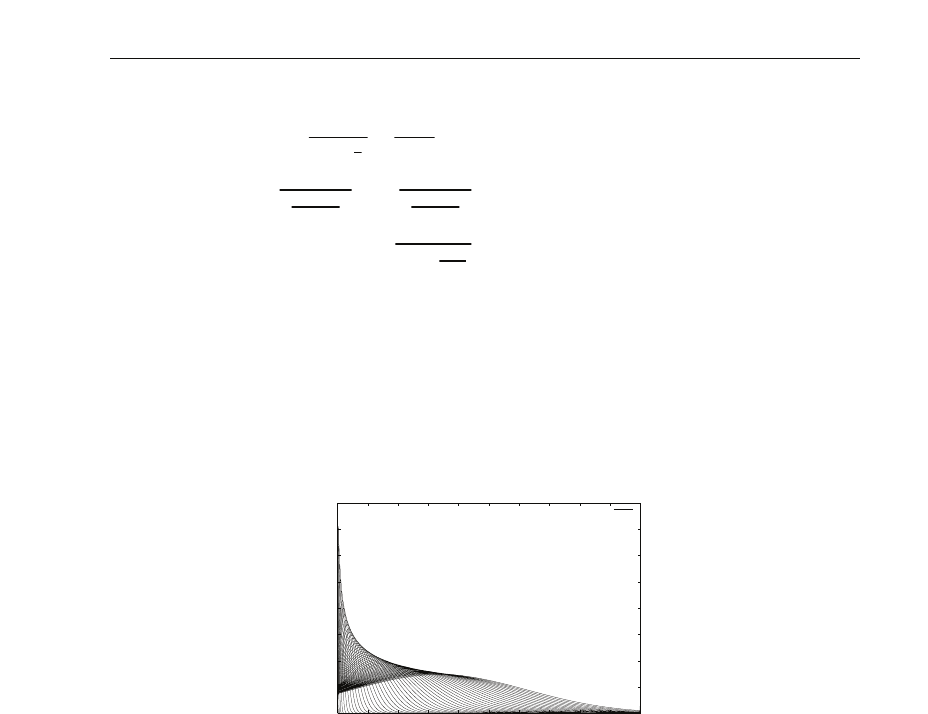
3.3 Numerical simulations
The evolution of n
e
(z) is depicted in Fig.(4). It is seen that n
e
(z) ≥ 0, and that its shape is
closely influenced by the expression used for S
e
(z).
0
1
2
3
4
5
6
7
8
0 5e-007 1e-006 1.5e-006 2e-006 2.5e-006 3e-006 3.5e-006 4e-006 4.5e-006 5e-006
ne(z)
x[m]
Fig. 4. Spatial distribution of n
e
(z) for various values E
kin
.
4. Transient see computation by a two-fluxes method
In section 4, the modelling borrows from Fitting’s papers, the absorption/diffusion
cross-section expressions as a function of electric field. It differs mainly in the governing
set of equations and in the numerical techniques that are used but also in the fact that some
comparison between numerical computations and experimental work are done.
4.1 Mathematical modelling
The mathematical modelling expresses the coupling between electric field with electron/hole
transport and describes the spatial and temporal charge trapping in an insulator submitted
to an electron beam irradiation. The temporal evolution of the secondary electron emission is
computed as a function of global trapped charge. It is given by a set of 7 nonlinear, coupled
equations.
95
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
8 Numerical Simulations, Applications, Examples and Theory
Fig. 5. Scheme of the modelling where R
p
is the penetration depth, φ the diameter of the
irradiated zone and L the dielectric thickness. The incident electron flux j
0
has a kinetic
energy E
kin
. Scheme of the modelling where R
p
(E
kin
) is the penetration depth, φ the diameter
of the irradiated zone and L the dielectric thickness. The incident electron flux j
0
has a kinetic
energy E
kin
. The electron fluxes j
e−
/j
e+
and the hole fluxes j
h−
/j
h+
are coupled by diffusion.
4.1.1 Purpose of the modelling
The purpose of this modelling is to analyze the evolution of the global trapped charge, per
unit surface, at time t, Q
p
(t) which is defined by:
Q
p
(t)=
L
0
ρ(z, t) dz +
|
e
|
n
s
(t) (22)
and the true secondary electron emission yield see
∗
(t) expressed as:
see
∗
(t)=κ
s
(
n
s
(t)
)
j
e−
(
0, t
)
j
0
(23)
where the expression of κ
(
n
s
(t)
)
is given in the next subsubsection.
The proposed modelling describes the interaction between the number of trapped electrons
n
ep
(z,t) and holes n
hp
(z,t) with the four current fluxes
(
j
c
)
c∈C
,thecurrentj
prim
(
z
)
and the
electric field E
(z,t).
4.1.2 Governing equation for the saturation effect of the surface trapping sites n
s
(t)
Defining by N
s
the number of trapping surface sites located at the interface z = 0andbyσ
s
their elementary cross section then the evolution of the number of traps per surface unit at
time t, n
s
(t) follows the equation
|
e
|
dn
s
(t)
dt
= j
e−
(0, t)
(
κ − κ
s
(
n
s
(t)
))
(24)
where κ
s
(
ns(t)
)
is defined by:
κ
(n
s
(t)) = κ exp
(
−
σ
s
(
N
s
− n
s
(t)
))
(25)
Its contribution is especially important during the initial charge injection phase for an amount
of time driven by the product σ
s
N
s
. The initial condition states that there are no surface
trapped charges.
96
Numerical Simulations - Applications, Examples and Theory

Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
9
4.1.3 Governing equation for the electric field E(z,t)
Here we assume that the electric field E(z,t) depends only on the total charge density ρ(z, t)
which is different from the trapped charge density. Using a two-fluxes method it was assumed
that only the trapped charge density contributed to the electric field. The local Maxwell-Gauss
equation writes
∇.E
(
z, t
)
=
ρ
(
z, t
)
0
r
, (26)
An electrostatic analysis taking into account polarization charges on the interface leads to
E
(
0, t
)
= −
1
0
r
(
1 + ε
r
)
1
1 +
πφ
2
/4
L
2
(
1+ε
r
)
Q
p
(t) −|e|
n
s
(t)
0
r
. (27)
where the second factor is introduced as corrections due to image charges in the sample
holder.
4.1.4 Governing equation for current fluxes j
c
(
z, t
)
The following balance is written
d
c
∂j
c
(z,t)
∂z
+
3
∑
i=1
W
c,i
= S
c
(z)+σ
di f f
c
(
E(z, t)
)
j
c
(z,t) (28)
where
(a) d
c
∂j
c
(z,t)
∂z
is the gradient of forward/backward electron/hole flux,
(b) W
c,1
= σ
di f f
c
(
E(z, t)
)
j
c
(z,t) is the flux loss by diffusion,
(c) W
c,2
=
σ
pc
N
pc
− n
cp
(z,t)
.j
c
(z,t), is the flux loss by trapping on unoccupied trapping
sites N
pc
− n
cp
(z,t),
(d) W
c,2
= σ
ac
n
ˆ
cp
(z,t)j
c
(z,t) is the flux loss by annihilation with trapped charge
ˆ
c,
(e) S
c
(z) is a source term for the creation of electrons or holes induced by the slowdown of
primary electrons.
(f) σ
di f f
c
(
E(z, t)
)
j
c
(z,t) is a positive source transport term by diffusion for dual charge of c,
i.e. travelling in the opposite direction.
The boundary conditions are s
c
sign dependant.
–Forbackwardfluxesj
e−
(
z, t
)
and j
h−
(
z, t
)
, the boundary condition at z = L means that the
bottom of the material has no charge injection:
∀c ∈
{
e−,h−
}
: j
c
(
L, t
)
=
0.
–Forforwardfluxes,j
e+
(
z, t
)
and j
h+
(
z, t
)
, the boundary condition at z = 0meansthe
continuity of the hole flux j
h+
(
0, t
)
=
j
h−
(
0, t
)
, but a discontinuity for the electron flux
j
e+
(
0, t
)
=
(
1 − κ
)
.j
e−
(
0, t
)
.
4.1.5 Governing equation for the charge density ρ
(
z, t
)
The temporal variation of the trapped charge density ρ(z,t) follows the conservation law
∂ρ
(
z, t
)
∂t
+ ∇.j
(
z, t
)
=
0, (29)
where the overall current flux of charges j
(
z, t
)
is such that
j
(
z, t
)
=
j
e−
(
z, t
)
−
j
e+
(
z, t
)
−
j
h−
(
z, t
)
+
j
h+
(
z, t
)
−
j
0
j
prim
(
z
)
. (30)
97
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method

10 Numerical Simulations, Applications, Examples and Theory
4.1.6 Governing equation for trapped charge Q
p
(t)
The temporal evolution of total trapped charge Q
p
(t) is defined from the total charge density
ρ
(z,t)=|e|
n
ep
(z,t) − n
hp
(z,t)
(31)
thanks to the equation
dQ
p
(t)
dt
=
L
0
dρ(z,t)
dt
= −j
e+
(L, t)+j
h+
(L, t)+j
0
(1 − see(t)). (32)
4.1.7 Governing equation for the trapped electrons n
ep
(
z, t
)
The evolution of the number of trapped electrons n
ep
(
z, t
)
follows the differential equation
|
e
|
∂n
ep
∂t
(
z, t
)
=
σ
pe
N
pe
− n
ep
(
z, t
)
(
j
e+
(
z, t
)
+
j
e−
(
z, t
))
−
σ
ah
n
ep
(
z, t
)(
j
h+
(
z, t
)
+
j
h−
(
z, t
))
(33)
which expresses the balance between
– the number of electrons that are trapped, where σ
pe
is the trapping cross section of the
electrons and N
pe
is the total number of electrons trapping sites,
σ
pe
N
pe
− n
ep
(
z, t
)
(
j
e+
(
z, t
)
+
j
e−
(
z, t
))
(34)
– and the number of trapped electrons present in the traps that are annihilated by free holes,
where σ
ah
is the annihilation cross section between trapped electrons and free holes.
σ
ah
n
ep
(
z, t
)(
j
h+
(
z, t
)
+
j
h−
(
z, t
))
. (35)
The absolute value,
|
e
|
of the electron charge in coulomb is introduced to transform the fluxes
(
j
c
(
z, t
))
c∈C
expressed in Coulomb into fluxes expressed in carriers numbers.
The initial condition n
ep
(
z,0
)
=
0, means that there are no trapped electrons at the beginning
of charge injection.
Remark 4.1 In order to simplify the notations, we define the total flux j
T
h,e
(z,t)=j
h+/e+
(z,t)+
j
h−/e−
(z,t), which is always positive, while the algebraic flux j
h,e
(z,t)=j
h+/e+
(z,t) − j
h−/e−
(z,t)
can be negative. We introduce functions a(z,t) and b(z,t) that are defined by the expressions
a
(z,t)=
σ
pe
j
T
e
(z,t)+σ
ah
j
T
h
(z,t)
/
|
e
|
≥
0,
b
(z,t)=
σ
pe
N
pe
j
T
e
(z,t)
/
|
e
|
≥
0.
then Eq.(33) can be rewritten
∂n
ep
∂t
(
z, t
)
+
a(z, t)n
ep
(z,t)=b(z,t) (36)
A straightforward computation shows that the formal solution of Eq.(33) is given by
n
ep
(z,t)=
t
0
exp
v
t
a(z,u) du
b(z, v)dv (37)
from which we can infer that n
ep
(z,t) ≥ 0.
98
Numerical Simulations - Applications, Examples and Theory

Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
11
4.1.8 Governing equation for the trapped holes n
hp
(
z, t
)
The evolution of the number of trapped holes n
hp
(
z, t
)
follows the differential equation
|
e
|
∂n
hp
∂t
(
z, t
)
=
σ
ph
N
ph
− n
hp
(
z, t
)
(
j
h+
(
z, t
)
+
j
h−
(
z, t
))
−
σ
ae
n
hp
(
z, t
)(
j
e+
(
z, t
)
+
j
e−
(
z, t
))
(38)
which expresses the balance between
– the number of holes that are trapped, where σ
ph
is the trapping cross section of the holes
and N
ph
is the total number of holes trapping sites,
σ
ph
N
ph
− n
hp
(
z, t
)
(
j
h+
(
z, t
)
+
j
h−
(
z, t
))
(39)
– and the number of trapped holes present in the traps that are annihilated by free electrons,
where σ
ae
is the annihilation cross section between trapped holes and free electrons.
σ
ae
n
hp
(
z, t
)(
j
e+
(
z, t
)
+
j
e−
(
z, t
))
(40)
The initial condition n
hp
(
z,0
)
=
0, means that there are no trapped holes at the beginning of
charge injection.
It is worth mentioning that trapped holes and trapped electrons have the same type of
behaviour, so the governing equations are symmetrical, when one exchanges the index h with
the index e.
4.2 Numerical scheme
The mathematical modelling expresses the nonlinear coupling between a set of seven
equations with seven unknowns E
(
z, t
)
,
(
j
c
(
z, t
))
c∈C
, n
ep
(
z, t
)
and n
hp
(
z, t
)
.Astraighforward
computation leads to a formal expression of each unknown as a function of the others
which involves spatial/temporal integrals and stiff exponential functions, but the non-linear
coupling remain. We are therefore led to use a numerical discretization scheme to compute
the solution of this one-dimensional nonlinear initial boundary value problem, expressed in
conservation form.
We present a full implicit conservative finite volume scheme on a non uniform staggered grid
used for the discretization of the governing set of equations on a geometrically refined grid
near the interface z=0. The computational domain is Ω.
– Unknowns that are located at the center of cell Ω
i
are n
ep
k
i
, n
hp
k
i
, ρ
|
k
i
,
– Unknowns that are located at the edges of cell Ω
i
are
E
|
k
i,i
+1
, j
e+
|
k
i,i
+1
, j
e−
|
k
i,i
+1
, j
h+
|
k
i,i
+1
, j
h−
|
k
i,i
+1
.
We use a backward Euler scheme, with constant time-step Δt, first order accurate in time, for
the temporal discretization, and note t
k
= k.Δt.
4.2.1 Discretization of the surface trapping sites n
s
(t) equation
A straightforward computation leads to the discrete equation
n
k+1
s
− n
k
s
Δt
=
j
e−
|
k+1
1
|
e
|
κ
− κ
s
(n
k+1
s
)
. (41)
99
Two-Fluxes and Reaction-Diffusion Computation
of Initial and Transient Secondary Electron Emission Yield by a Finite Volume Method
12 Numerical Simulations, Applications, Examples and Theory
The stiffness induced by the exponential term present in κ
s
(n
k+1
s
) requires a first order
linearization, hence the iterative solution by a fixed point technique is given by
n
k+1,p+1
s
− n
k,p
s
Δt
=
j
e−
|
k+1,p
1
|
e
|
(
κ − w
p
)
)
, (42)
w
p
= κ
s
(n
k+1,p
s
)+
n
k+1,p+1
s
− n
k+1,p
s
κ
s
(n
k+1,p
s
). (43)
Then the value of n
k+1,p+1
s
is easily determined.
4.2.2 Discretization of the charge density equation
Integrating Eq.(29) over control volume Ω
i
leads to the discrete equation
h
i
ρ
k+1
i
− ρ
k
i
+ Δt
j
k+1
i
+1
− j
k+1
i
= 0. (44)
A decoupled iterative solution thanks to the fixed point method leads to the computation,
where p is the nonlinear iteration index
ρ
k+1,p+1
i
= ρ
k
i
−
Δt
h
i
j
k+1,p
i
+1
− j
k+1,p
i
. (45)
4.2.3 Discretization of the trapped charge equation
The discretization is straightforward and leads to the equation
Q
p
k+1
− Q
p
k
Δt
= − j
e+
|
k+1
I
+1
+ j
h+
|
k+1
I
+1
+ j
0
1
− see
k+1
. (46)
A decoupled iterative solution thanks to the fixed point method leads to the computation,
where p is the nonlinear iteration index
Q
p
k+1,p+1
= Q
p
k,p
+ Δt
− j
e+
|
k+1,p
I
+1
+ j
h+
|
k+1,p
I
+1
+ j
0
1
− see
k+1,p
. (47)
4.2.4 Discretization of the electric field equation
The discretization is straightforward and leads to the equation
E
k+1
i
+1
− E
k+1
i
=
h
i
ρ
k+1
i
0
r
, (48)
E
k+1
1
= −
1
0
r
(
1 + ε
r
)
1
1 +
πφ
2
/4
L
2
(
1+ε
r
)
Q
k+1
p
−|e|
n
k+1
s
0
r
. (49)
A decoupled iterative solution thanks to the fixed point method leads to the computation,
where p is the nonlinear iteration index.
E
k+1,p+1
i
+1
= E
k+1
i
+
h
i
ρ
k+1,p
i
0
r
, (50)
E
k+1,p+1
1
= −
1
0
r
(
1 + ε
r
)
1
1 +
πφ
2
/4
L
2
(
1+ε
r
)
Q
k+1,p
p
−|e|
n
k+1,p
s
0
r
. (51)
100
Numerical Simulations - Applications, Examples and Theory
