Андреев Е.Б., Ключников А.И. и др. Автоматизация технологических процессов добычи и подготовки нефти и газа

Подождите немного. Документ загружается.

131

ние регулятора, в свою очередь находится под его обратным воз-

действием.

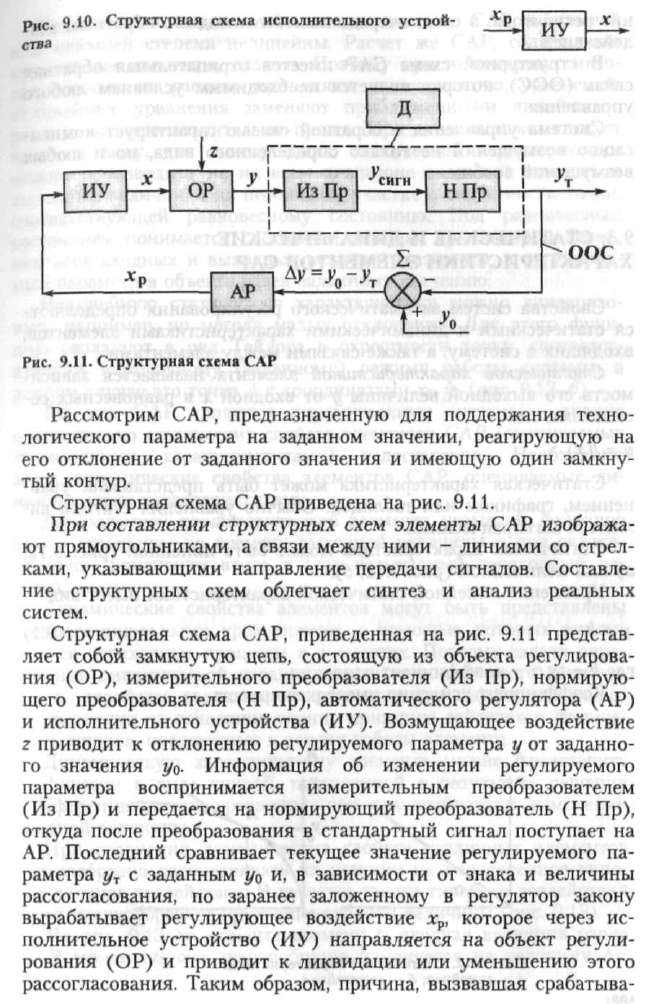
В структурной схеме САР имеется отрицательная обратная

связь (ООС), которая является необходимым условием любого

управления.

Система управления с обратной связью гарантирует компен-

сацию возмущений не только определенного вида, но и любых

возмущений вообще.

9.3. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ

ХАРАКТЕРИСТИКИ ЭЛЕМЕНТОВ САР

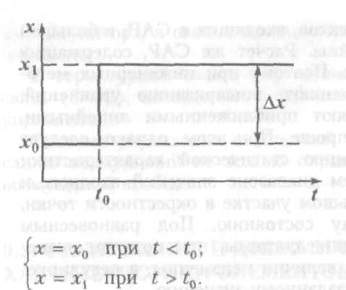
Реакцию элемента на скачкообразное изменение входной ве-

личины называют временной характеристикой. Уравнение вре-

менной характеристики может быть получено в результате реше-

ния дифференциального уравнения при входном скачкообразном

воздействии. По найденному выражению может быть построен

график временной характеристики.

Глава 10

УСТОЙЧИВОСТЬ И КАЧЕСТВО САР

10.1. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ

Для исследования различных по природе и конструкции сис-

тем регулирования с помощью единого математического аппарата

их представляют в виде структурных схем. Такие схемы содер-

жат динамические звенья и различные способы их соединения.

В основу классификации звеньев положены соответствующие

уравнения динамики.

Под динамическим звеном понимают уравнение динамики,

которым можно представить различные по физической природе

и конструкции элементы САР.

Динамические звенья называют элементарными, так как они

не могут быть разложены на более простые. А так как каждое из

них (в зависимости от его динамических свойств) может быть

отнесено к тому или иному типу, их называют также типовыми.

Динамические звенья называют типовыми, если изменение

проходящего через них сигнала описывается алгебраическим или

134

Рис. 9.13. График скачкообразного

изменения входной величины

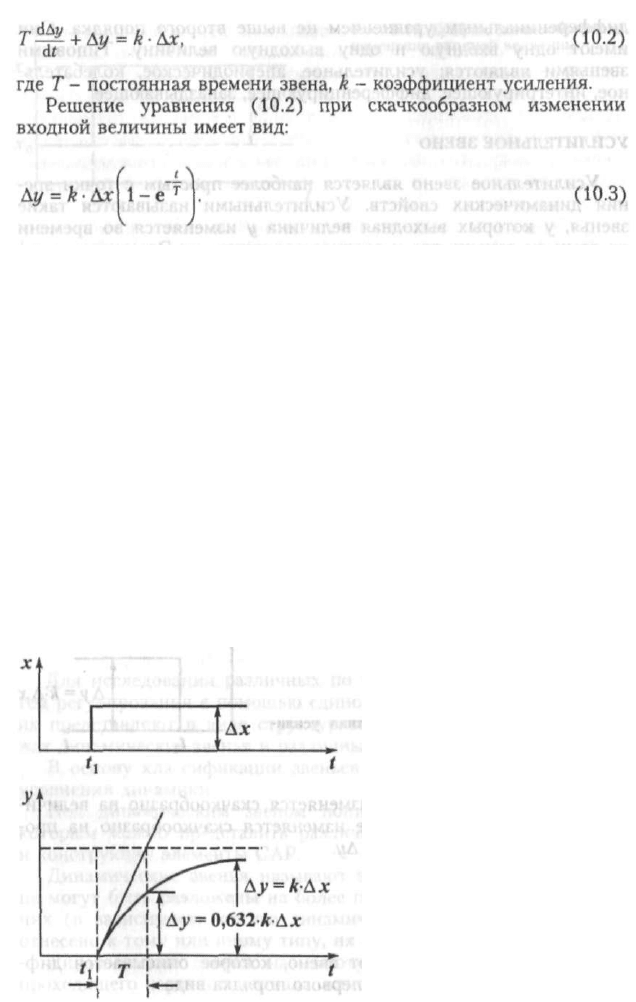
Временная характеристика апериодического звена, построен-

ная по выражению (10.3), представлена на рис. 10.2 и является

экспонентой. Из графика видно, что выходная величина со вре-

менем стремится к новому равновесному значению. Теоретически

время переходного процесса равно бесконечности. Практически

же можно считать, что переходный процесс заканчивается за

время, в течение которого отклонение Ау достигает 95 % от мак-

симального отклонения, соответствующего новому состоянию

равновесия звена. Это время, равное обычно ЗГ, называют вре-

менем разгона.

Постоянную времени Т звена можно определить из временной

характеристики. Если из любой точки экспоненты провести каса-

тельную до пересечения с прямой, характеризующей новое уста-

новившееся значение выходной величины, то проекция этой ка-

сательной на ось времени и будет величиной Т. На рис. 10.2 ка-

сательная проведена из начальной точки кривой. Постоянная

времени Т имеет размерность времени. Из графика рис. 10.2 вид-

Рис. 10.2. Временная характери-

стика апериодического звена

136

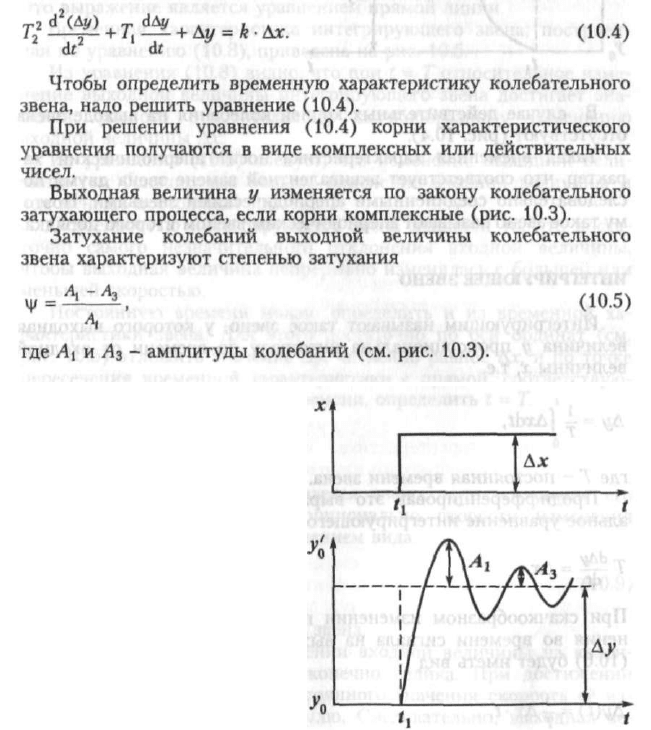
Рис. 10.3. Временная характеристи-

ка колебательного звена

137

но, что за время Т отклонение выходной величины под действи-

ем скачкообразного изменения входной величины достигает

63,2 % от максимального отклонения.

КОЛЕБАТЕЛЬНОЕ ЗВЕНО

Колебательным называют звено, если после скачкообразного

изменения его входной величины х изменение выходной у имеет

форму затухающих колебаний.

Динамические свойства такого звена выражаются дифферен-

циальным уравнением вида:

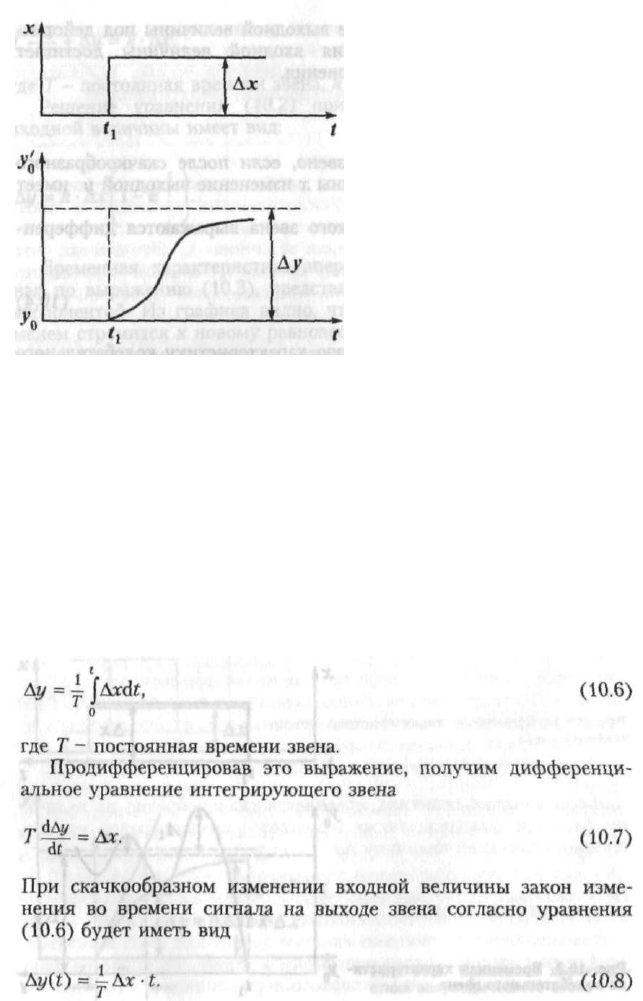
Рис. 10.4. Временная характеристи-

ка апериодического звена второго

порядка

В случае действительных корней колебания на выходе звена

отсутствуют (рис. 10.4).

Такая временная характеристика носит апериодический ха-

рактер, что соответствует эквивалентной замене звена двумя по-

следовательно соединенными апериодическими звеньями. Поэто-

му такое звено называют апериодическим звеном второго порядка.

ИНТЕГРИРУЮЩЕЕ ЗВЕНО

Интегрирующим называют такое звено, у которого выходная

величина у пропорциональна интегралу по времени от входной

величины х, т.е.

138

Это выражение является уравнением прямой линии.

Временная характеристика интегрирующего звена, построен-

ная по уравнению (10.8), приведена на рис, 10.5.

Из уравнения (10.8) видно, что при t = Г относительное изме-

нение выходной величины интегрирующего звена достигает зна-

чения, равного относительному скачкообразному изменению

входной величины Ах.

Из уравнения (10.8) следует, что изменение выходной вели-

чины тем больше, чем больше изменение входной величины и

чем меньше постоянная времени Т.

Особенностью интегрирующего звена является то, что доста-

точно самого незначительного отклонения входной величины,

чтобы выходная величина непрерывно изменялась с большей или

меньшей скоростью.

Постоянную времени можно определить и из временной ха-

рактеристики звена. Для этого достаточно по оси ординат (см.

рис. 10.5) отложить значение Ау, численно равное Ах, и по точке

пересечения временной характеристики с прямой, соответствую-

щей Ах и параллельной оси времени, определить t = Т.

ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО

Дифференцирующим называется звено, если изменение его

выходной величины у пропорционально скорости изменения

входной х и описывается уравнением вида:

Рис. 10.5. Временная характеристи-

ка интегрирующего звена

Рис. 10.6. Временная характеристика идеаль-

ного дифференцирующего звена

личина получает в момент изменения мгновенный импульс, ве-

личина которого изменяется от нуля до бесконечности и снова

возвращается к нулю. Изменение выходной величины при скач-

кообразном изменении входной показано на рис. 10.6.

Из анализа уравнения (10.9) видно, что ни одно реальное зве-

но не может в точности удовлетворить ему, так как в реальных

элементах систем автоматического регулирования невозможны

мгновенные процессы. Звенья, описываемые уравнением (10.9),

называют идеальными.

Реальным дифференцирующим звеном называют такое звено,

для которого зависимость между изменениями входной и выход-

ной величин определяется уравнением

Рис. 10.7. Временная характеристика

реального дифференцирующего звена

140