Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Том 2

Подождите немного. Документ загружается.

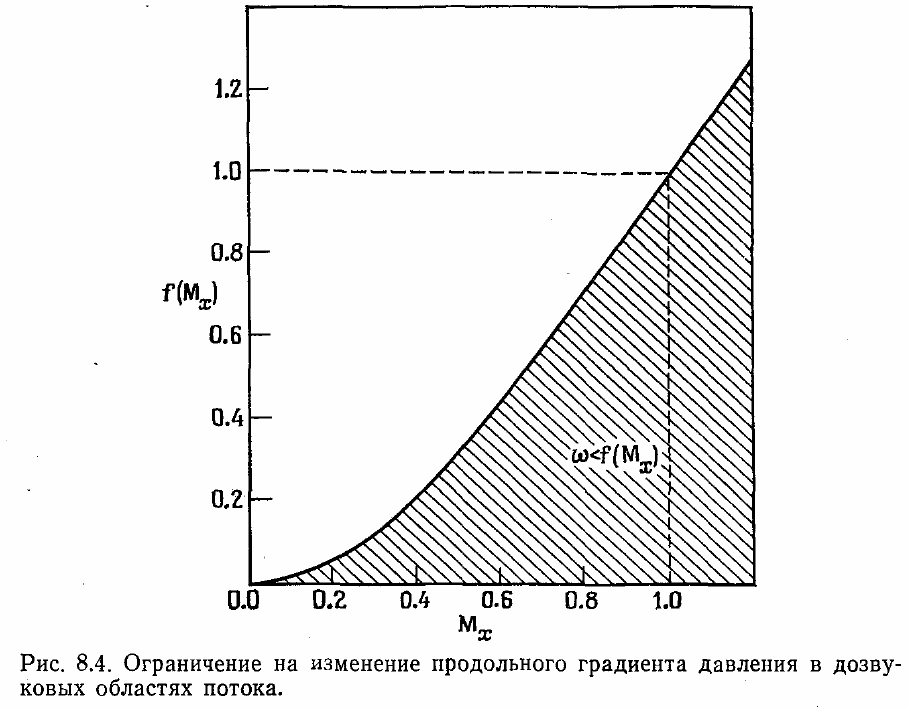
жительными. Заметим также, что

стремится к нулю вблизи

стенки, где Мх =0. Таким образом, мы видим, что решения параболизованных

уравнений Навье—Стокса, полученные маршевым методом по пространственной

координате, подвержены неустойчивостям (расходящиеся решения), когда

продольный градиент давления полностью сохраняется в дозвуковых частях

пограничного слоя, так как тем самым вводится в них элемент эллиптичности.

Предложены различные способы преодоления этой трудности, и мы их сейчас

обсудим.

Самый очевидный способ борьбы с неустойчивостью — полностью отбросить

градиент давления в дозвуковых зонах. Это даст устойчивую маршевую схему, но и

приведет к ошибкам для полей течений с большими продольными градиентами дав-

ления. Следует, однако, заметить, что вариации давления в продольном

направлении будут по-прежнему сказываться на численном решении в случае, если

давление определяется из уравнения движения по координате у и уравнения

энергии. Альтернативный подход состоит в задании изменения продольного

градиента давления. Очевидно, приравнивание нулю градиента давления — один из

путей того, как это можно осуществить. Если продольный градиент давления

определен, его можно исключить из матриц [A

] и [A

] в уравнениях (8.44) и (8.48) и

рассматривать как источниковый член в задаче нахождения собственных значений.

Следовательно, продольный градиент давления уже не будет влиять на

математическую природу уравнений. При решении уравнений пограничного слоя

продольный градиент давления обычно известен из расчета внешнего течения

невязкой жидкости или в случае внутренних течений определяется из закона

сохранения массы. К сожалению, при решении параболизованных уравнений Навье

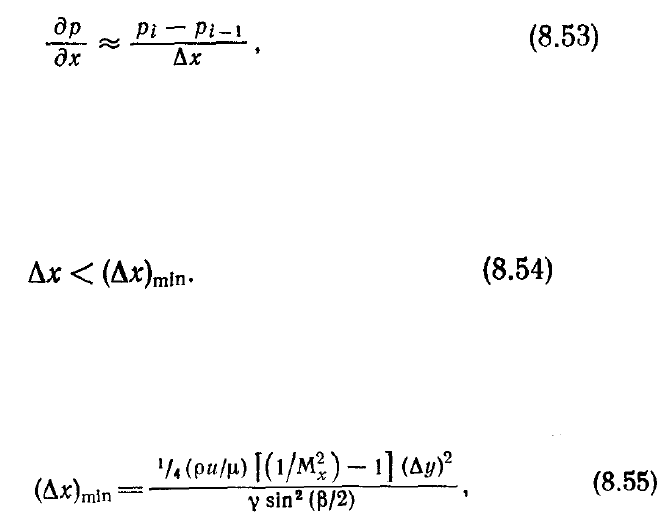
— Стокса продольный градиент давления заранее неизвестен и должен вычисляться

в процессе решения.

В некоторых работах продольный градиент давления был сохранен и в

дозвуковых зонах и аппроксимировался разностями назад, которые рассчитываются

с использованием информации с предыдущего слоя по маршевой координате.

Например, когда рассчитывается решение на слое i+1, производная др/дх

представляется в виде

т. е. это есть разность назад первого порядка. Лубард и Хеллиуэлл [Lubard, Helliwell,

1973] исследовали устойчивость (расходимость), используя разности назад для

продольного градиента давления в уравнениях движения и энергии. Они применили

неявную разностную схему и показали при помощи анализа устойчивости по Фурье,

что неустойчивость будет иметь место, если

Это условие устойчивости очень необычно, так как обыкновенно из анализа

устойчивости по Фурье вытекает, что неустойчивость будет иметь место, если

∆

больше некоторого (

∆

max

. Когда такой анализ был произведен для двумерных

параболизованных уравнений Навье—Стокса (8.48)—(8.49), то оказалось, что

где

—волновое число (k

∆

у). Лубард и Хеллиуэлл показали также, что если

продольный градиент давления аппроксимировать на неявном слое, как и все

остальные члены параболизованных уравнений, то минимальный допустимый шаг

(

∆

min

удваивается. Чтобы объяснить столь необычное условие устойчивости, Рубин

[Rubin, 1981] высказал предположение, что (

∆

min

является размером области

передачи эллиптического взаимодействия вверх по потоку. Если (

∆

x) > (

∆

min

, то

это взаимодействие как бы «не замечается» и маршевая процедура устойчива. В

противном случае, если (

∆

x) < (

∆

min

, численное решение пытается учесть это

эллиптическое взаимодействие, что ведет к расходящимся решениям, поскольку

передача влияния вверх по потоку в маршевой процедуре запрещена. Рубин и Лин

[Rubin, Lin, 1980] показали, что размер области эллиптического взаимодействия

имеет порядок толщины дозвуковой зоны. Поэтому если дозвуковая зона

сравнительно большая, то минимальная допустимая величина

∆

x может быть

слишком велика для осуществления точных (или устойчивых) вычислений.

Другой метод учета градиента давления в продольном направлении называется

приближением подслоя. Первыми его предложили Рубин и Лин [Rubin, Lin, 1971], а

позже он был применен для параболизованных уравнений Навье — Стокса Шиффом

и Стегером [Schiff, Steger, 1979]. В приближении подслоя градиент давления в

вязкой дозвуковой области вычисляется в точке вне подслоя, в которой скорость

сверхзвуковая. Такое приближение основано на том, что в тонком дозвуковом

вязком подслое др/ду пренебрежимо мало. Так как градиент давления задается в

дозвуковой зоне, то маршевый по пространственной координате метод даст, видимо,

устойчивое решение. Однако, как наблюдали Шифф и Стегер, в некоторых случаях

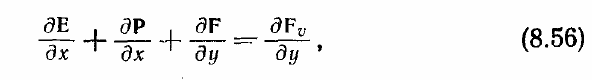
возможны всё же расходящиеся решения. Они могут быть обусловлены

взаимодействием через давление сверхзвуковых и дозвуковых областей, которое

описывается нормальным уравнением движения и уравнением энергии.

Новый метод учета продольного градиента давления предложили Виньерон и др.

[Vigneron et al., 1978a]. В этом подходе в дозвуковой вязкой зоне часть продольного

градиента давления

(др/дх) в уравнении сохраняется, а остальная (1 —

) (др/дх)

либо опускается, либо рассчитывается на явном слое при помощи разностей назад

или приближения подслоя. Уравнение (8.41) переписывается в виде.

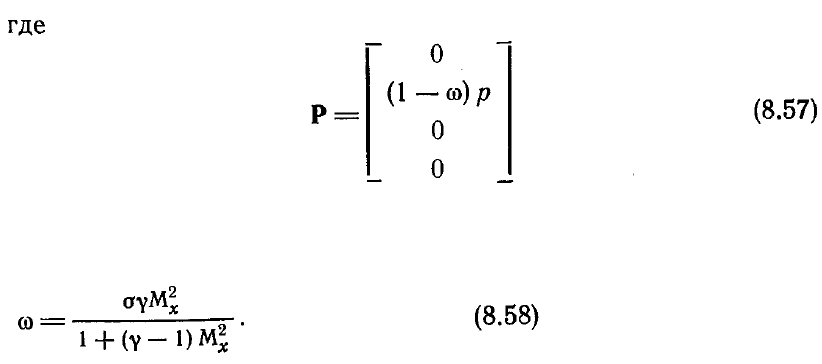
и Е, F и F

определяются уравнениями (8.42). Параметр

вычисляется по

уравнению (8.47) с некоторым коэффициентом запаса

Виньерон и др. [Vigneron et al., 1978b] для анализа устойчивости использовали

метод Фурье. Для уравнения (8.56) с опущенным членом дF/ду они применили

простую неявную схему (неявную схему Эйлера), а производная дР/дх

аппроксимировалась разностью назад. Как и ожидалось, они обнаружили, что если

рассчитываемый на явном слое градиент давления опущен, то маршевый по

пространственной координате метод будет всегда давать устойчивое решение, так

как уравнения остаются гиперболически-параболическими. Если этот член остается,

то возникает неустойчивость, когда (

∆

x) меньше некоторого (

∆

min

. Оказалось, что

при

= 0 (

∆

min

задается зависимостью (8.55), что подтверждает результаты более

ранних работ Лу-барда и Хеллиуэлла. Существуют и другие способы представления

продольного градиента давления [Lin, Rubin, 1979; Buggein et al., 1980; Yanenko et

al., 1980].

Во многих задачах механики жидкости эллиптические эффекты передачи влияния

вверх по потоку сравнительно малы и в упомянутых выше методах удается

предотвратить возникновение неустойчивостей, причем довольно точное решение

получается за одно-единственное прохождение поля течения. В других задачах, в

которых влияние распространения возмущений вверх по потоку велико (из-за

отрыва, наличия следа или ударной волны и т. п.), эти методы оказываются

несостоятельными. В результате возникает неустойчивость или предпринимаемые

для ее подавления меры приводят к большим ошибкам. В этих случаях можно

использовать процедуру глобальной релаксации по давлению [Rubin, Lin, 1980]. В

ней сначала задается некоторое распределение давления во всем поле течения для

определения градиента давления в каждой точке. Начальное распределение

давления можно получить, либо полагая предельный градиент давления равным

нулю, либо применяя метод Виньерона с дР/дх = 0, либо беря достаточно большие

∆

x . Зная градиент давления, параболизованные уравнения Навье — Стокса можно

решить с помощью устойчивой, конечно-разностной маршевой процедуры при

условии, что градиент давления аппроксимируется надлежащим образом. Это реше-

ние дает новое распределение давления, которое можно использовать для расчета

градиента давления, необходимого при следующем прохождении расчетной

области. Такая итерационная процедура продолжается до получения сходимости.

Для адекватного моделирования эллиптического характера поля течения градиент

давления должен влиять на течение вверх по потоку. Этого можно добиться,

аппроксимируя его разностями вперед, т. е. когда вычисляется решение на слое i+1,

градиент давления представляют в дискретном виде

Такого рода дискретизация возможна только при использовании глобальной

релаксационной процедуры по давлению, так как обычно p

i+2

нам неизвестно. Рубин

и Лин исследовали устойчивость, когда др/дх аппроксимируется разностью вперед,

и показали, что имеет место безусловная устойчивость. Однако мы приближаемся к

границе устойчивости, когда дозвуковые области становятся очень большими.

Глобальная релаксационная процедура по давлению представляется

многообещающей для задач, в которых влияние вверх по потоку существенно.

Однако следует помнить, что эта процедура требует значительно больших затрат

машинного времени, нежели типичные расчеты параболизованных уравнений Навье

— Стокса с одним прохождением поля течения. В некоторых случаях затраты

машинного времени сравнимы с теми, которые требуются для расчета полных

уравнений Навье — Стокса. Следовательно, для этих задач параболизованные урав-

нения Навье — Стокса уже не обладают никакими преимуществами по сравнению с

полными уравнениями Навье — Стокса.

8.3.3. Численное решение параболизованных уравнений Навье — Стокса

Как отмечалось ранее, параболизованные уравнения Навье—Стокса образуют

смешанную систему гиперболически-параболических уравнений относительно

координаты х в продольном направлении при выполнении следующих условий:

1) невязкий поток сверхзвуковой;

2) продольная компонента скорости всюду отлична от нуля;

3) градиент давления в уравнении движения по продольной координате либо

опущен, либо неустойчивость подавляется одним из способов, описанных в

предыдущем разделе.

Если эти условия соблюдены, параболизованные уравнения Навье—Стокса

можно решать конечно-разностными методами, сходными с теми, которые

используются для решения параболических уравнений пограничного слоя. Поэтому

устойчивая маршевая по пространственной координате процедура может ис-

пользоваться для получения решения во всей расчетной области, начиная с

поверхности задания начальных данных и далее вниз по потоку до выходного

сечения.

Некоторые из решений параболизованных уравнений Навье—Стокса,

опубликованных ранее, были получены с использованием явных схем. Это было

сделано скорее для удобства, нежели из соображений эффективности, так как в гл. 7

было показано, что неявные схемы для уравнений этого типа более эффективны. В

более поздних работах для решения параболизованных уравнений Навье — Стокса

применялись самые разные неявные алгоритмы: неявная схема переменных направ-

лений Писмена—Ракфорда [Nardo, Cresci, 1971], неявные схемы с итерациями

[Rubin, Lin, 1972; Lubard, Helliwell, 1973]. Схема предиктор-корректор с

итерациями, которую предложили Рубин и Лин, была описана в п. 4.5.10, где она

применяется для решения трехмерного линейного уравнения Бюргерса

Линейное трехмерное уравнение Бюргерса — полезная модель параболизованных

уравнений Навье—Стокса, однако, разумеется, она не передает нелинейный

характер последних. Так, когда схема предиктор-корректор с итерациями

применяется к параболизованным уравнениям, то возникают нелинейные члены

типа

()

k,j,i

,где т - номер итерации, х = i

∆

x , у == i

∆

у , z = i

∆

z. Они

линеаризуются методом Ньютона — Рафсона (см. п. 7.3.3), т. е. если f = f(x

, х

, ...,

), то

где х

обозначает зависимые переменные. Применение этой формулы к нелинейному

члену (уй

/,^)

дает

После линеаризации таким способом всех нелинейных членов получаемую систему

алгебраических уравнений (на итерации т + 1) можно решать при помощи

эффективной процедуры для блочных трехдиагональных систем. Итерирование

продолжается, пока не будет получено сходящееся решение в сечении i + 1. Этот

метод неявный по координате у, градиенты по которой наибольшие, но явный по

координате z (см. п. 4.5.10), что приводит к следующему условию устойчивости для

трехмерных параболизованных уравнений Навье — Стокса:

До недавнего времени параболизованные уравнения Навье—Стокса решались

при помощи неявных разностных схем с итерациями вроде той, которая была

описана выше. Виньерон и др. [Vigneron et al., 1978a] впервые предложили более

эффективную неявную приближенно факторизованную схему без итераций. Этот

алгоритм, принадлежащий к классу неявных схем. переменных направлений,

разработан целой группой авторов [Lindemuth, Killeen, 1973, McDonald, Briley, 1975;

Beam, Warming, 1978] и приспособлен для решения зависящих от времени

уравнений, например уравнений Навье—Стокса. Чтобы разобраться в нем,

применим его для решения трехмерных параболизованных уравнений Навье —

Стокса, записанных в декартовых координатах (х—продольное направление) в слу-

чае совершенного газа. Тогда

Векторы Е

, F

, G

, F

и G

задаются выражениями (8.35) и содержат

параболизованные члены со сдвиговыми напряжениями и тепловыми потоками

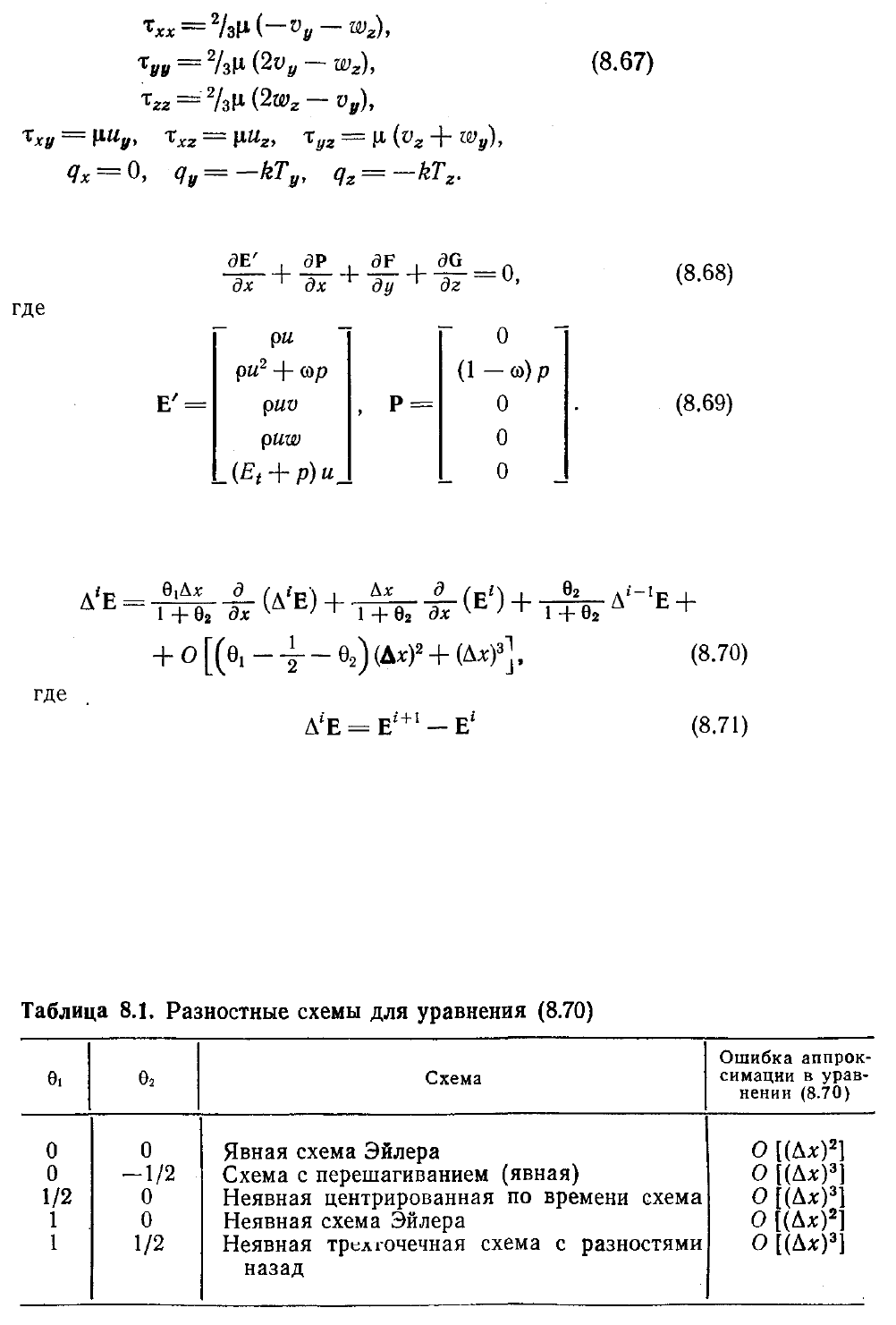
Чтобы, следуя Виньерону, представить градиент давления в направлении течения, Е

можно заменить Е' + Р; тогда уравнение (8.65) примет вид

Решение уравнения (8.65) получается маршевым по координате х методом с

использованием следующей разностной формулы, предложенной Бимом и

Уормингом [Beam, Warming, 1978]:

и х =i

∆

x. Эта разностная формула общего вида за счет выбора параметров

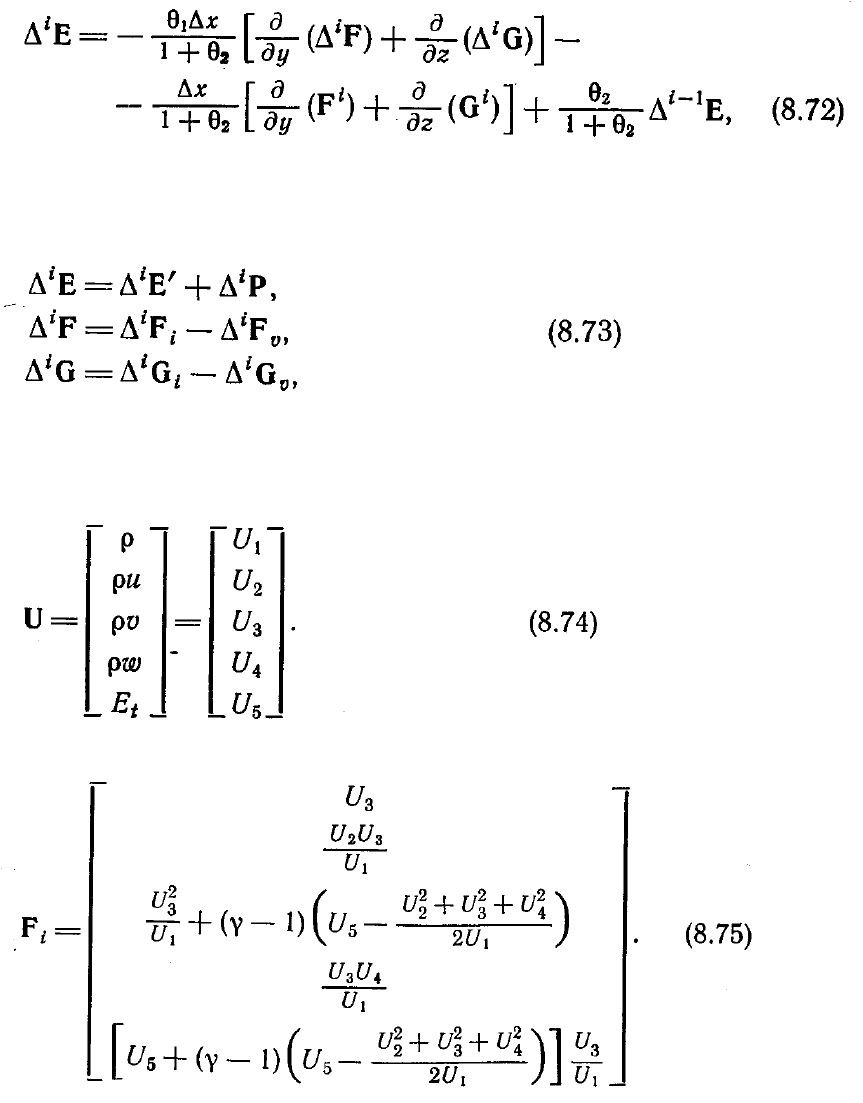
позволяет получать многие обычные разностные схемы, которые перечисляются в

табл. 8.1. Для параболизованных уравнений Навье—Стокса используется обычно

либо неявная схема Эйлера первого порядка (

= 1,

=0), либо трехточечная схема

второго порядка с разностями назад (

= 1,

=1/2). Как показали Бим и Уорминг,

неявная центрированная по времени схема второго порядка (

=1/2,

= 0)

приводит к неустойчивости в случае ее применения к параболическим уравнениям.

Отметим, что в табл. 8.1

приводится ошибка аппроксимации для

∆

Е. Когда в разностной схеме производная

дЕ/дх заменяется на

∆

Е /

∆

x -, ошибка делится на

∆

Подстановка уравнения (8.65) в (8.70) дает

где член с ошибкой аппроксимации опущен. Это разностное соотношение записано

в так называемой дельта-форме, упомянутой в п. 4.4.7. Дельта-члены

∆

Е,

∆

F и

∆

которые можно записать в виде

линеаризуются разложением в ряд Тейлора. Чтобы линеаризовать невязкие дельта-

члены

∆

Е,

∆

F и

∆

G, воспользуемся тем фактом, что Е’, F

и G

, являются

функциями только вектора U:

Например, F

, можно выразить через компоненты вектора U следующим образом:

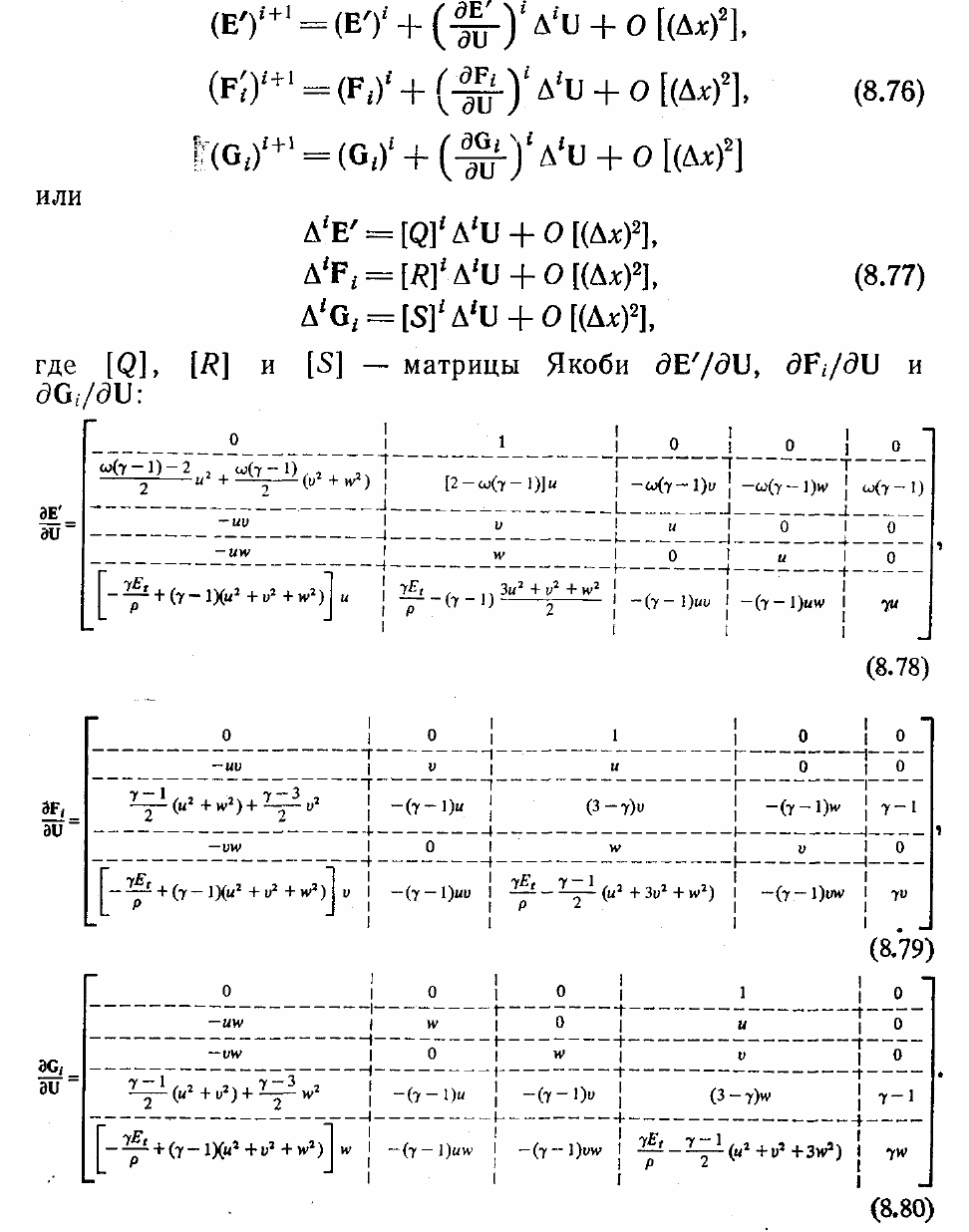
Следовательно, мы легко можем разложить Е’, F

и G

в ряд

Выражение для матрицы Якоби дE'/дU получено в предположении, что

локально

не зависит от U.

Вязкие дельта-члены можно линеаризовать методом, который предложил Стегер

[Steger, 1977]. В нем коэффициенты вязкости

и теплопроводности k считаются

локально не зависящими от U и пренебрегают вязкими членами со смешанными

производными. В результате элементы F

и G

имеют следующий общий вид: