Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Том 2

Подождите немного. Документ загружается.

Численные методы решения параболизованных уравнений Навье—Стокса

§ 8.1. Введение

Уравнениями пограничного слоя можно пользоваться для расчета многих течений

вязкой жидкости, как было показано в гл. 7. Имеется, однако, ряд важных задач

динамики вязкой жидкости, которые не могут быть решены при помощи уравнений

пограничного слоя. В этих задачах допущения пограничного слоя просто

несправедливы. Например, если имеет место полное слияние вязкого и невязкого

потоков, то их нельзя рассчитывать независимо друг от друга, как это делается в

теории пограничного слоя. Поэтому приходится решать систему уравнений,

справедливую как в невязкой, так и в вязкой областях течения.

На рис. 8.1 изображены некоторые поля течений, для описания которых

уравнения пограничного слоя непригодны. Гиперзвуковое течение разреженного

газа вблизи заостренной входной кромки плоской пластины (рис. 8.1 (а)) является

классическим примером вязкого потока, который нельзя рассчитывать при помощи

уравнений пограничного слоя. Фактически в непосредственной близости от входной

кромки газ нельзя даже считать сплошной средой, так что в этой части поля течения

неприменимы и уравнения Навье—Стокса. В области слившегося слоя, когда газ

уже можно рассматривать как сплошную среду, ударная волна и вязкий слой слиты

в одно целое и неотличимы друг от друга. Ниже по течению ударный слой можно

рассматривать как разрыв и между ним и вязким слоем возникает явно выраженная

область невязкого потока. Отсюда начинается область взаимодействия, которая

далее делится на области сильного и слабого взаимодействия.

Течение в области слабого взаимодействия по мере продвижения вниз по

потоку в конечном счете развивается в классическое прандтлевское погранслойное

течение. Очевидно, уравнениями пограничного слоя нельзя пользоваться в области

слившихся слоев, так как вязкий слой и ударная волна слиты друг с другом

абсолютно неразличимо. В начале области сильного взаимодействия вязкое течение

нельзя рассчитывать независимо от невязкого из-за того, что они сильно

взаимодействуют друг с другом. В области слабого взаимодействия уже возможен

расчет вязкой и невязкой частей поля течения независимым образом, но это следует

делать путем итераций, как показано в гл. 7.

Другими словами, сначала рассчитываются уравнения пограничного слоя с

приближенно заданными граничными условиями на внешней границе. Затем можно

рассчитать невязкую часть течения с поправкой на толщину вытеснения, что дает

новые уточненные условия на внешней границе для следующей итерации в

пограничном слое. Эту процедуру можно повторять, пока решение во всей области

не будет меняться от итерации к итерации. За исключением случаев очень слабого

взаимодействия, замечено, что такая итерационная процедура часто менее

эффективна, чем решение уравнений, пригодных как для вязкой, так и для невязкой

областей поля течения [Davis, Rubin, 1980].

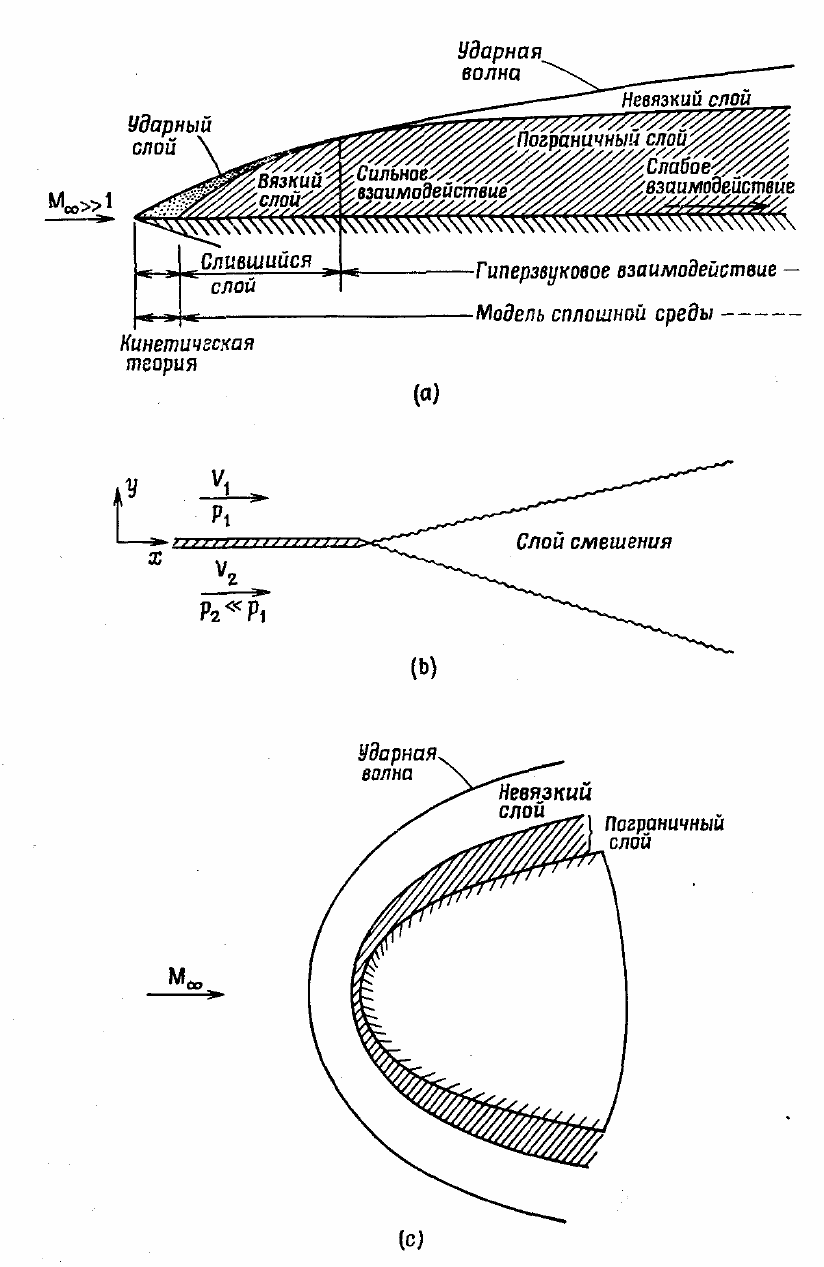
На рис. 8.1(b) изображено течение в слое смешения, для которого уравнения

пограничного слоя (уравнения тонкого сдвигового слоя) неприменимы. Поперек

слоя смешения существует сильный градиент давления. Следовательно, обычные

уравнения пограничного слоя (уравнения тонкого сдвигового слоя), содержащие

уравнение движения в нормальном направлении в виде

в этом случае непригодны и требуется более полное уравнение движения в

нормальном направлении. Другой пример поля течения, которое нельзя описать

уравнениями пограничного слоя—сверхзвуковое обтекание затупленного тела на

больших высотах (рис. 8.1 (с)). В пространстве между ударной волной и телом (т. е.

в ударном слое) существует сильное взаимодействие между пограничным слоем и

невязким течением, поэтому для расчета такого течения используют уравнения,

пригодные для обеих областей (вязкого и невязкого течений).

На рис. 8.1(d) изображено течение в двугранном угле (угле, образованном двумя

пересекающимися плоскостями). Это наш последний пример течения, когда

уравнения пограничного слоя неприменимы. Как показано в гл. 7, в уравнения

пограничного слоя включаются производные только по одной, так называемой

нормальной координате. Вблизи вершины двугранного угла производные, входящие

в вязкие члены, по обоим нормальным направлениям будут величинами одного

порядка. Такого рода конфигурации часто встречаются, например, в каналах прямо-

угольного сечения и в местах сочленения крыло—фюзеляж.

Очевидно, что полные уравнения Навье—Стокса можно использовать для

расчета полей течений, изображенных на рис. 8.1, как впрочем и любого другого

течения, для которого неприменимы уравнения пограничного слоя. В некоторых

случаях только их и можно применять. К сожалению, уравнения Навье — Стокса с

трудом поддаются решению, поскольку это сопряжено с большими затратами

машинного времени и памяти. Особенно это верно в отношении уравнений Навье—

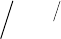
Стокса для сжимаемой жидкости, которые образуют смешанную систему

эллиптически-параболических уравнений для стационарных течений и

гиперболически-параболических уравнений для нестационарных течений. Обычно

даже для расчета стационарного течения применяется зависящая от времени

процедура решения, т. е. нестационарные уравнения Навье — Стокса инте-

грируются по времени до тех пор, пока не будет достигнуто установившееся

решение. Таким образом, при расчете трехмерного течения с использованием

уравнений Навье — Стокса для сжимаемого газа необходимо решать

четырехмерную (три пространственных измерения и время) задачу. Методы

решения полных уравнений Навье—Стокса будут обсуждаться в гл. 9.

К счастью, во многих задачах расчета вязких течений, в которых уравнения

пограничного слоя нельзя применять, можно решать систему уравнений, которая по

сложности занимает промежуточное положение между полными уравнениями На-

вье—Стокса и уравнениями пограничного слоя. Эти уравнения принадлежат к

классу так называемых уравнений Навье—Стокса в приближении тонкого слоя или

параболизованных уравнений Навье — Стокса. В этот класс попадает несколько

систем уравнений. Назовем некоторые из них: уравнения Навье—Стокса в

приближении тонкого слоя, параболизованные уравнения Навье—Стокса, частично

параболизованные уравнения Навье—Стокса, уравнения вязкого ударного слоя, ко-

нические уравнения Навье—Стокса.

Системы уравнений этого класса характеризуются тем, что их можно применять

как в невязкой, так и в вязкой областях поля течения. Кроме того, во всех этих

уравнениях содержится ненулевой градиент давления в нормальном направлении.

Это совершенно необходимо для того, чтобы течения в вязкой и невязкой областях

можно было бы решать одновременно.

Когда эти уравнения используются вместо полных уравнений Навье—Стокса, это

имеет два очень больших преимущества. Во-первых, эти уравнения состоят из

меньшего количества членов, что приводит к сокращению времени счета. Во-

вторых, что более важно, в стационарном случае большинство систем этого класса

состоит из гиперболически-параболических уравнений по координате ^

направлении основного потока (при соблюдении некоторых условий). Другими

словами, уравнения Навье—Стокса «параболизуются» в продольном направлении.

Как следствие этого их можно решать маршевыми методами типа применяемых в

теории пограничного слоя, что уменьшает число измерений с четырех до трех

пространственных. Тем самым достигается существенная экономия памяти и

уменьшается время счета. В этой главе мы обсудим вывод уравнений, относящихся

к типу уравнений Навье — Стокса в приближении тонкого слоя, и некоторые

методы их решения.

§ 8.2. Уравнения Навье — Стокса в приближении тонкого слоя

Формально нестационарные уравнения пограничного слоя можно получить,

пренебрегая в полных уравнениях Навье—Стокса членами порядка

Re и выше.

Вследствие такого анализа порядка величин все вязкие члены с производными по

направлению, параллельному поверхности тела, опускают, так как они существенно

меньше вязких членов с производными по направлению, нормальному к стенке.

Помимо этого, уравнение движения в нормальном направлении сводится к совсем

простому уравнению типа уравнения (8.1) в декартовой системе координат,

означающему, что нормальный градиент давления очень мал. В приближении

тонкого слоя в нестационарных уравнениях Навье—Стокса вязкими членами с

производными по направлениям, параллельным поверхности тела, также прене-

брегают, но остальные члены в уравнениях движения сохраняются. Одно из

основных достоинств сохранения членов, которыми обычно пренебрегают в теории

пограничного слоя, заключается в возможности прямого расчета отрывных и

возвратных течений. Без труда рассчитываются также и течения с большими

градиентами давления в нормальном направлении типа изображенных на рис. 8.1.

Концепция приближения тонкого слоя возникает также из детального

рассмотрения типичных случаев численного решения полных уравнений Навье—

Стокса при больших числах Рей-нольдса [Baldwin, Lomax, 1978]. В этих расчетах

значительная часть ресурсов ЭВМ тратится на вычисление нормальных градиентов

в пограничном слое, так как для этого необходима сетка с очень малым шагом. В

результате градиенты в направлениях, параллельных поверхности тела, обычно не

разрешаются адекватным образом, даже если соответствующие вязкие члены и

сохраняются в уравнениях. Следовательно, при численном решении уравнений

Навье—Стокса во многих случаях имеет смысл опускать члены, которые не

разрешаются адекватным образом, при условии что они малы. Эти соображения

приводят к уравнениям Навье—Стокса в приближении тонкого

слоя.

Упрощая полные уравнения Навье—Стокса в соответствии с приближением

тонкого слоя, для изображенного на рис. 8.2 течения получаем в декартовой системе

координат следующие уравнения:

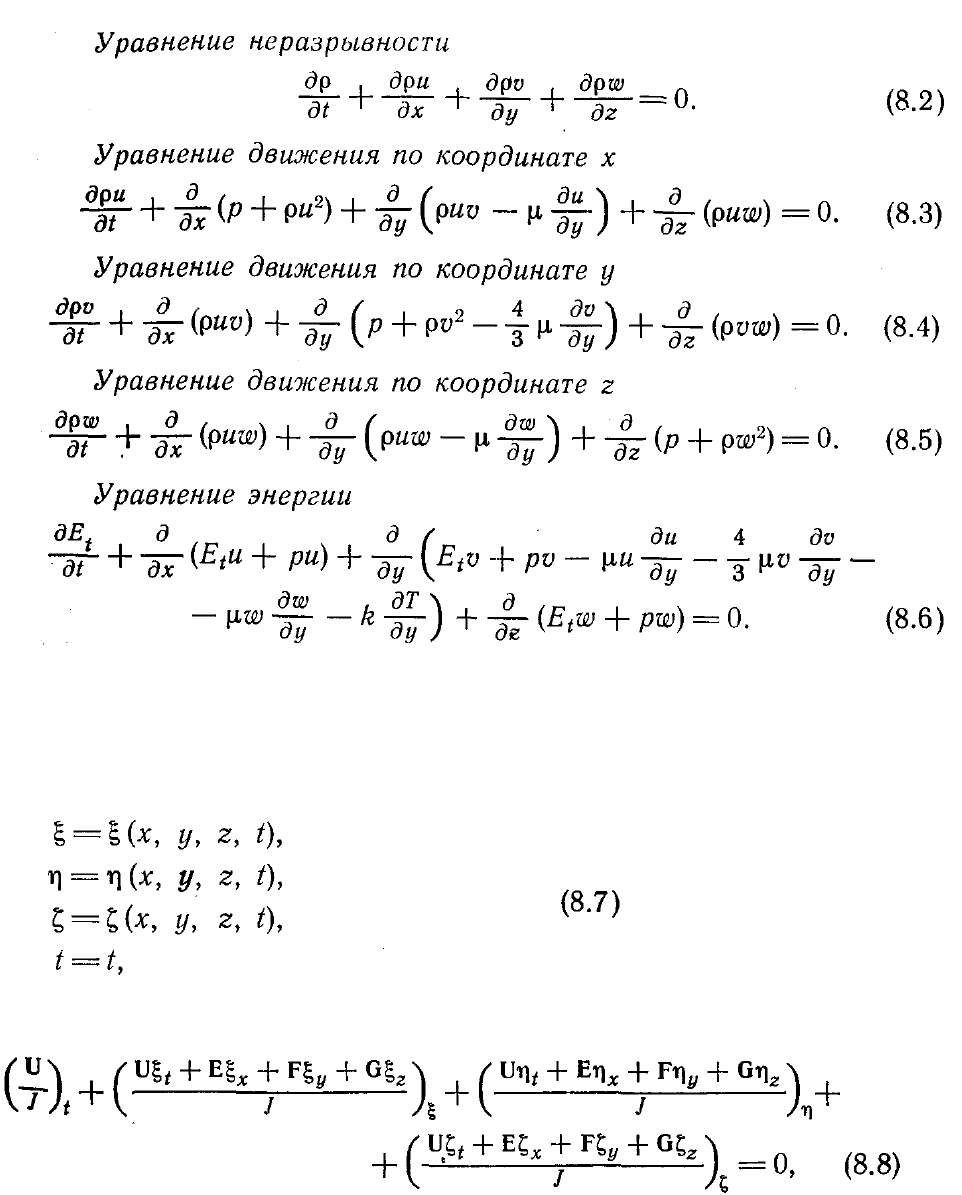
Эти уравнения записаны для случая ламинарного течения, но их легко

модифицировать и для турбулентного течения, используя методику § 5.4.

Для тел более сложной формы необходимо отобразить поверхность тела из

физического пространства на вычислительное и уже в нем применять приближение

тонкого слоя. Зададим это отображение преобразованием общего вида

и пусть поверхность тела определяется уравнением

(

РИС

8.3). Преобразованные

уравнения в строго дивергентной форме имеют вид

тде J—якобиан преобразования и U, Е, F и G определяются Уравнениями (5.44).

Теперь применим приближение тонкого слоя к преобразованным уравнениям

Навье—Стокса. В рамках этого приближения можно пренебречь всеми вязкими

членами, содержащими частные производные по направлениям

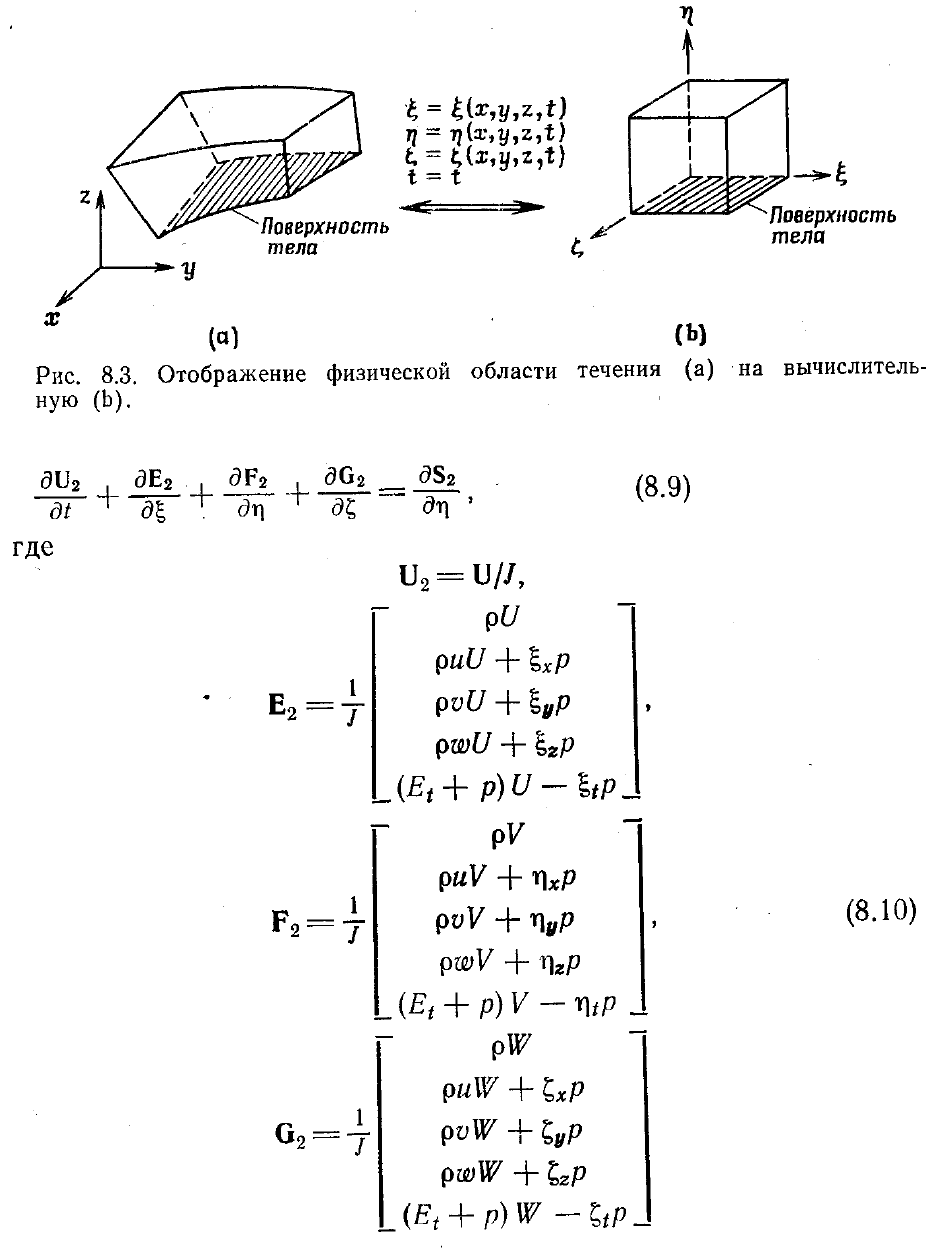
Полученные уравнения тонкого слоя можно записать в следующем виде:

и все вязкие члены содержатся в

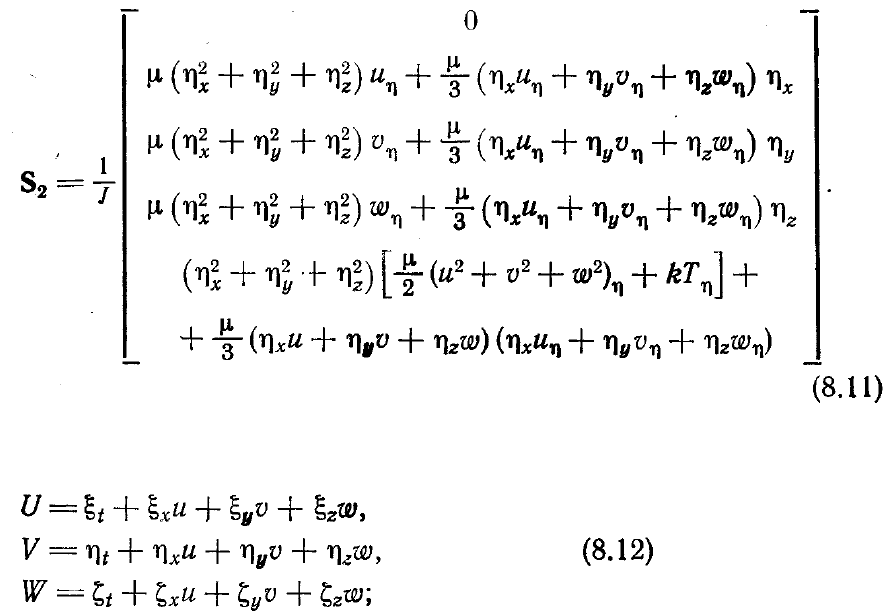
Для компактности выражения (8.10) записаны через контравариантные компоненты

скорости U, V и W, которые определяются в виде

U, V, W суть контравариантные компоненты скорости в направлениях, нормальных

к поверхности постоянства

; соответственно.

Хотя уравнения Навье — Стокса в приближении тонкого слоя существенно

проще полных уравнений Навье—Стокса, все же требуются значительные ресурсы

ЭВМ для их численного решения. Уравнения тонкого слоя образуют смешанную

систему гиперболически-параболических уравнений в частных производных

относительно времени. Следовательно, для их решения можно использовать методы

решения уравнений, зависящих от времени, как это обычно делают при решении

уравнений Навье—Стокса для сжимаемого газа. Поэтому отложим обсуждение

конечно-разностных методов решения уравнений тонкого слоя до гл. 9, в которой

будут подробно рассматриваться методы решения полных уравнений Навье—

Стокса.

§ 8.3. Параболизованные уравнения Навье — Стокса

Параболизованные уравнения Навье—Стокса получили в последнее время

широкое распространение, потому что их применение позволяет весьма эффективно

рассчитывать сложные стационарные трехмерные сверхзвуковые течения вязкого

газа.

Эффективность такого расчета обусловлена применением маршевых по

координате конечно-разностных схем, тогда как для решения полных уравнений

Навье—Стокса применяются маршевые по времени схемы. Поэтому затраты

ресурсов ЭВМ на решение параболизованных уравнений Навье—Стокса во всем

поле течения для сверхзвукового потока сравнимы с затратами на расчет только

невязкой части поля течения по уравнениям Эйлера или только вязкой части по

уравнениям пограничного слоя. Далее, поскольку параболизованные уравнения

Навье—Стокса справедливы и в вязкой, и в невязкой областях течения,

взаимодействие последних автоматически учитывается в расчетах по этим

уравнениям.

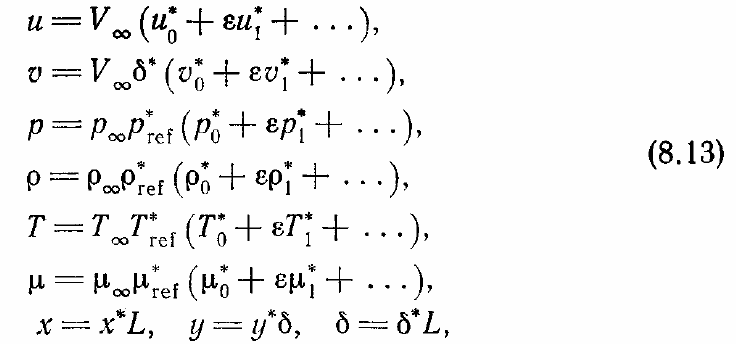
Термин «параболизованные» уравнения Навье—Стокса несколько неточен, так

как на самом деле эти уравнения при выполнении некоторых условий образуют

смешанную систему гиперболически-параболических уравнений. Эти условия вклю-

чают требования того, чтобы внешний невязкий поток был сверхзвуковым, а

продольная компонента скорости всюду была положительна. Заметим, что

последнее исключает возможность расчета отрыва в продольном направлении, хотя

отрыв в поперечном направлении возможен. Еще одно ограничение связано с

наличием продольного градиента давления в уравнении движения вдоль продольной

координаты. Если этот член включать во всем поле течения, тогда происходит

передача влияния вверх по потоку в дозвуковой части пограничного слоя, что

делает маршевый метод плохо обусловленным. Это ведет к экспоненциально

растущим решениям, часто называемым расходящимися. Было предложено

несколько способов преодоления этого затруднения, и вкратце они будут

обсуждены ниже.

8.3.1. Вывод параболизованных уравнений Навье — Стокса

В общем случае вывод параболизованных уравнений Навье—Стокса из полных

уравнений Навье—Стокса является не таким строгим, как вывод уравнений

пограничного слоя. По этой причине возникло несколько слегка отличающихся

версий параболизованных уравнений. Навье—Стокса. Их различие обусловлено

типом рассматриваемого течения. Однако во всех случаях нормальные градиенты

давления в уравнениях сохраняются, а вторые производные по продольному

направлению опускаются.

Одно из самых ранних исследований с использованием параболизованных

уравнений выполнили Рудман и Рубин [Rudman, Rubin, 1968]. Они рассчитали

сверхзвуковое ламинарное течение в окрестности входной кромки плоской

пластины (см. рис. 8.1 (а)). Рудман и Рубин получили параболизованные уравнения

из полных уравнений Навье—Стокса при помощи разложения в ряд. Такой метод

упрощения уравнений Навье— Стокса является альтернативой методу, основанному

на анализе порядка величин и использованному в гл. 5 для вывода уравнений

пограничного слоя. При разложении в ряд переменные сначала обезразмеривают по

некоторым локальным характерным параметрам течения, чтобы можно было

оценить порядок величин разных членов в уравнениях Навье—Стокса. Затем

производят разложение в ряд. Рудман и Рубин предложили делать это в следующем

виде:

где член с нижним индексом ref есть характерный местный параметр течения,

обезразмеренный по параметру свободного потока, L—характерная длина по

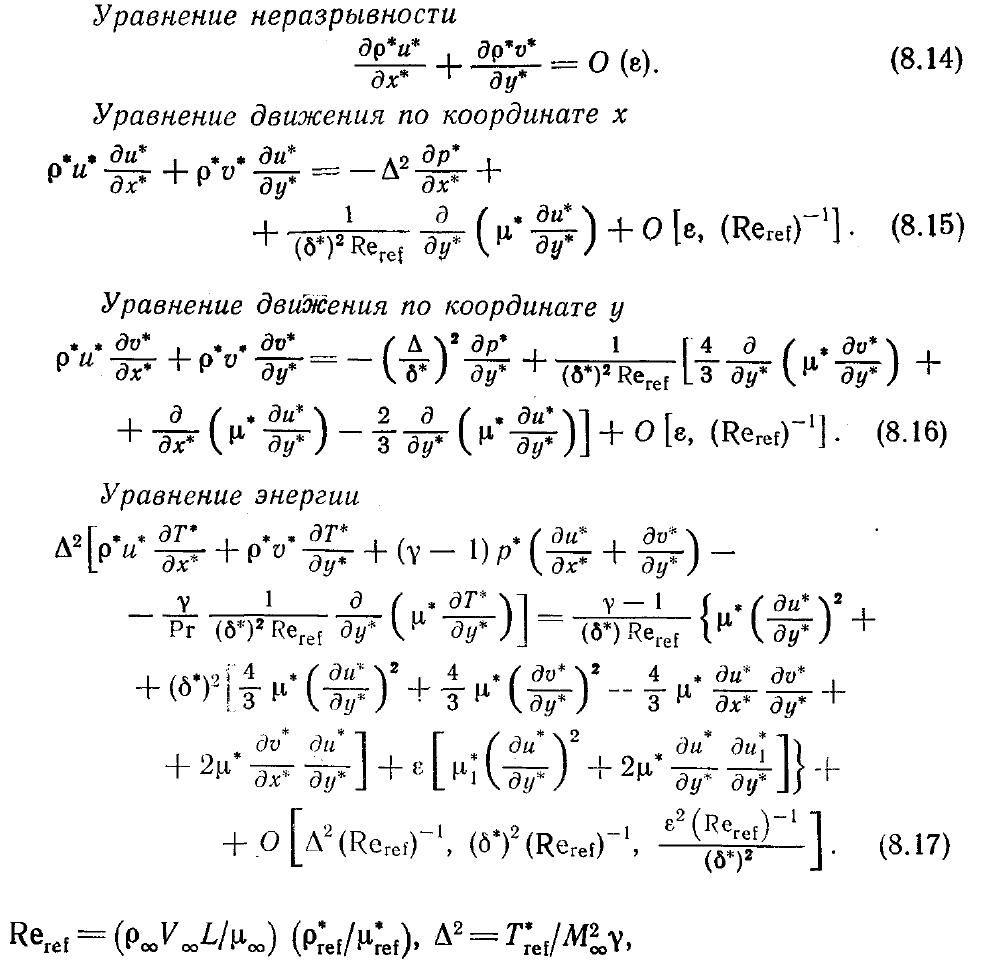
координате х и

—характерная длина по координате у. Первый член разложения,

обозначенный нижним индексом 0, используется для получения решения нулевого

порядка, тогда как для получения решения первого порядка необходимы и первый,

и второй члены. Для относительно тонкой возмущенной области, показанной на рис.

8.1 (а), нормальные к поверхности градиенты много больше градиентов в

направлениях, параллельных поверхности, и

* можно полагать малой величиной.

Подставляя это разложение в двумерные стационарные уравнения Навье—

Стокса, получаем следующие безразмерные уравнения (для удобства нижний

индекс 0 опущен):

В выписанных выше уравнениях

а газ полагается совершенным.

Следующий шаг состоит в том, чтобы выявить члены, которыми можно

пренебречь по сравнению с другими в уравнениях (8.14)—(8.17). Для этого

необходимо оценить порядки величин Re

ref

∆

и (

∆

в различных областях поля

течения. Из теории пограничного слоя известно, что в тонком вязком слое величина

ref

имеет порядок 1/(

. К тому же на начальном участке вязкого слоя

∆