Амелин Р.В., Блинков Ю.А. и др. Основные понятия информатики

Подождите немного. Документ загружается.

Для однозначного описания семантики целесообразно выбрать математическую

форму описания, т. е. сопоставление математических объектов для описания

конструкций языка.

Язык программирования предоставляет как простые операторы, так и методы

композиции, которые позволяют формировать структурные операторы из других

простых или составных операторов. Поэтому для описания семантики языка

программирования нужно решить две связанные между собой задачи.

1. Определить виды используемых в языке программирования простых операторов,

а также часто используемые методы композиции решений подзадач.

2. Обеспечить правила вывода, позволяющие определить эффект воздействия

простого оператора на состояние вычисления, а также вывести определенные

свойства составного оператора из свойств составляющих его компонент.

Ниже мы проиллюстрируем формальное определение семантики на примере

простого модельного языка содержащего основные конструкции и правила

композиции, встречающиеся в современных языках программирования .

Фундаментальное свойство основных правил композиции современных языков

программирования заключается в том, что они дают возможность объединить в

одну сложную структурную схему с одним входом и одним выходом, которая имеет

вид, изображенный на рис. 3.1

Рис 3.1.

Здесь S — оператор, группа операторов или программа; Р — предусловие —

логическое выражение, которое должно быть истинным перед выполнением S; Q —

постусловие — логическое выражение, которое должно принимать истинное

значение при выходе из вычислений S. Если ввести в язык понятие комментария

как произвольного текста, заключенного в фигурные скобки, то свойство,

изображенного на рис 3.1. можно в тексте программы записать как:

(1) {P} S {Q}

Это — спецификация программы S со следующим смыслом: если соотношение Р

истинно перед выполнением S, то Q будет истинно после выполнения S.

Пусть Р некоторое логическое выражение. Для простоты будем полагать, что

кванторы всеобщности и существования не принадлежат Р. Для выражения

)(Px

∀

считаем, что вхождение переменной х в

∀

связано квантором всеобщности и

каждое вхождение х в Р –связанное значение. Та же терминология применяется к

выражению

)(Px∃ , за исключением того, что в этом случае вхождение переменной

х в

∃

называют связанным квантором существования. Каждое вхождение переменной

х в логическое выражение, которое не связано квантором , называют свободной

переменной этого выражения.

Пример 1

• все переменные в выражении

))(( xyyx

≤

∀

∃ связаны;

• все переменные в выражении

)()( kjji

свободны.

Определим понятие подстановки.

Пусть P - логическое выражение. Нотация

(2)

используется для выражения, которое получается в результате

систематической подстановки выражения у вместо всех свободных вхождений

переменной х в Р. Аналогично

(3)

xnx

yny

...1

обозначает одновременную подстановку вместо всех свободных вхождений любой

переменной x

в P соответствующего выражения y

. Вхождения x

в некоторые y

не

замещаются. Переменные x

...x

должны быть различными, в противном случае

подстановка не определена.

Пример 2.

( 10) ( 10)

()

abc

xyz

zxy

x y ababc

xy xyxyz

==+=

+ =++++

Правила вывода - это схемы рассуждений, позволяющие доказывать свойства

программы. Они имеют следующий вид:

(4)

,...,

Если H

,…,H

— истинные утверждения, то H — также истинное утверждение.

Рассмотрим правила вывода для простых операторов языка программирования.

Пустой оператор

Он не оказывает никакого воздействия на значения программных переменных.

Для любого P имеем правило вывода

(5) {P}{P}

Оператор присваивания

Он имеет вид x = e и устанавливает значение переменной x равным значению

выражения e. Тогда для любого P

(6) {

P } x:=e {

}

Пример 3.

{x+y=10} z:=x+y {z=10}

{x-y>0} x:=x-y {x>0}

Рассмотрим правила вывода для более сложных конструкций - составных и

условных операторов.

Составной оператор

Он образуется путем последовательной композиции операторов S

; S

;…;S

. Знак

; используется для соединения операторов в последовательность. В модельном

языке составной оператор (или блок операторов) представлен программной

конструкцией:

(7) begin S

; S

;…;S

end

Правило вывода для составного оператора имеет вид:

(8)

}{ ;...;; }{

}{}{,...,1

210

iii

PendSSSbeginP

PSPni

−

∀

Пример 4.

Дан составной оператор

Z: = z+y

u := u-1

Известно постусловие

Q = (z+u*y = x*y, u≥0)

Тогда согласно правилу вывода для оператора присваивания легко установить

{z+(u-1)*y = x*y, u-1≥0} u := u-1 {z+u*y = x*y, u≥0}

{z+u*y = z+y+(u-1)*y = x*y, u>0} z := z+y {z+(u-1)*y = x*y, u-1≥0}

Следовательно, для рассматриваемого составного оператора справедливо

{z+u*y=z+y+(u-1)*y=x*y, u>0} begin z := z+y; u := u-1 end {z+u*y=x*y, u≥0}

Нетрудно заметить, что логическое выражение z+u*y=x*y сохраняется при

выполнении составного оператора. Логические выражения, сохраняемые

прорграппной конструкцией называются инвариантами. Нетрудно заметить, что в

нашем примере выполнение отдельных операторов присваивания в составном

операторе не сохраняет инвариант. Выражение z+u*y=x*y инвариантно для всего

составного оператора

Условный оператор

Если S

и S

- операторы, а B - булево выражение, то

(9)

endifSelseSthenBif

есть оператор, выполняющий следующие действия: вычисляется B; если B=true,

то выполняется оператор S

, в противном случае — S

. Пусть предусловие этого

оператора есть P, а постусловие — Q.

Тогда если значение B есть true, то оператор S

будет иметь постусловие Q,

если справедливо соотношение

(10) {P ∧ B} S

{Q}

Аналогично для оператора S

должно быть справедливо соотношение

(11) {P ∧ ¬B} S

{Q}

Объединяя (10,11) можно получить правило вывода для условного оператора

(12)

}{}{

}{}{},{}{

QendifSelseSthenBifP

RSBPQSBP

∧

Рассмотрим более простую форму условного оператора

(13)

EndifSThenBIf

По этому оператору вначале вычисляется B. Если B истинно, то выполняется

оператор S, иначе должна быть выполнена тождественная операция. Правило

вывода для оператора (13) имеет вид

(14)

}{}{

},{}{

QSThenBIfP

QPQSBP ⇒

∧

Пример 5.

Легко доказать, что оператор

If r<y Then r := r-y; q :=q+1 EndIf

сохраняет истинным предикат q*y+r=x, r≥0 при условии y>0. В самом деле,

составной оператор удовлетворяет соотношению

(q*y+r=x,0≤r<y} r := r-y; q := q+1 {q*y+r=x,r≥0}

Тогда согласно (14),

{q*y+r=x, 0≤r} If r<y Then r := r-y; q = q+1 EndIf {q*y+r=x,r≥0},

а это означает инвариантность предусловия.

Селективный оператор выбора

Он имеет вид

(15) Select Case x

Case k

;

...

Case k

EndSelect

Оператор Case выбирает для выполнения тот оператор-компоненту, метка

которого k

совпадает с текущим значением селектора x. Если такой метки не

обнаружено, то действие оператора (16) не определено. Очевидно, если

требуется, чтобы Q было справедливым независимо от того, какой оператор S

выбирается для выполнения, мы имеем набор соотношений:

(17) {P

∧(x=k

)} S

{Q}, i=1..n

Тогда правило вывода для оператора выбора должно иметь вид:

(18)

)...(

}{:;...:])},...,[({

,...,1}{)}({

111

nnn

iii

PPPP

QEndSelectSkCaseSkCaseCaseSelectkkxP

niдляQSkxP

∧∧∧=

∈∧

∧

Оператор цикла с предусловием

Если B - булево выражение, а S - оператор, то

(19)

WendSBWhile

обозначает итерационное выполнение оператора S пока B истинно. Если B

ложно с самого начала, то S не будет выполняться совсем. Процесс итерации

заканчивается, когда В становится ложным. Определим правило вывода для этого

оператора. Если Р - его предусловие, то предусловие для оператора S имеет вид

P∧B. Для итерационного повторения выполнения оператора S в цикле его

постусловие должно совпадать с P. Следовательно, оператор S должен

удовлетворять соотношению

{P∧B} S {P}

Оператор цикла с предусловием завершит свою работу, если справедливо

P∧¬B

Итак, получаем следующее правило вывода для оператора с предусловием

(17)

}{}{

PWendSBWhileP

PSBP

∧

Далее будем называть Р инвариантом цикла.

Пример 6.

Рассмотрим оператор цикла

While r >= y

r := r-yz;

q := 1+q

Wend

в предположении, что {x≥0 ∧ y>0}. Покажем, что данный цикл имеет инвариант

x=q*y+r ∧ 0≤r

Согласно правилам вывода для оператора присваивания и составного оператора

легко получаем соотношение

{x=q*y+r ∧ 0≤r-y} r:=r-y; q:=q+1 {x=q*y+r ∧ 0≤r}

Предусловие составного оператора имеет форму P∧B. Поэтому для

рассматриваемого цикла справедливо согласно (20) соотношение:

{(x=q*y+r) ∧ 0≤r} While r>=y r:=r-y; q=q+1 Wend {(x=q*y+r) ∧ 0≤r<y}

Оператор цикла с постусловием

(21)

BUntilLoopSDo

Где S – оператор (составной) и B - булево выражение. Здесь S выполняется

перед вычислением B. Затем, если В ложно, процесс итерационного выполнения S

продолжается, в противном случае он завершается.

Предположим, доказано, что {P} S {Q} и Q∧¬B⊃P. Тогда возможно повторное

выполнение оператора S. Выход из цикла влечет за собой условие Q∧B. Тогда

правило вывода для цикла с постусловием имеет вид

(22)

}{}{

)(},{}{

BQBUntilLoopSDoP

PBQQSP

∧

⇒

∧

Пример 7.

Пусть дан цикл с постусловием

z := z+y;

u := u-1

Loop Until u = 0

Предположим, что x, y — переменные целого типа, которые удовлетворяют

условию x>0 ∧ y>0. Пусть требуемое постусловие цикла есть {z=x*y}. Очевидно,

если объединить его с условием завершения цикла u=0, то его можно переписать

в виде z+u*y=x*y. Используя правила вывода для операторов присваивания и

составного оператора “z=z+y u=u-1” легко показать, что он имеет предусловие и

постусловие {z+u*y=x*y}. Отсюда легко получить числитель правила вывода (22):

{z+u*y=x*y} z := z+y; u := u-1 {z+u*y=x*y}, {z+u*y=x*y} ∧ u>0

Отсюда и из правила вывода (22) следует, что

{z+u*y=x*y} z := z+y; u := u-1 {{z+u*y=x*y}∧ u=0}

Очевидно, полученное постусловие эквивалентно {z=x*y}. Следует обратить

внимание, что неявно мы здесь воспользовались еще одной группой правил вывода

- правилами консеквенции.

Правила консеквенции

имеют вид

(23)

}{}{

}{}{,

}{}{

},{}{

QSP

QSRRP

QSR

QRRSP ⇒⇒

Таким образом, мы строго определили семантику основных операторов

некоторого гипотетического языка программирования посредством формальных

правил вывода.

4.3. Корректность программ.

Правильность программ обычно проверяется тестированием. Оно заключается в

том, что выбираются конкретные значения входных данных программы и программа

выполняется с этим входными данными. Результаты работы программы сравниваются

с заранее известными правильными результатами.

Тестирование - процесс выполнения программы с намерением найти ошибку. Но

оно никогда не докажет их отсутствия. Поэтому необходимо абстрагироваться от

индивидуальных процессов и постулировать некоторые общезначимые условия,

которые можно вывести из характера поведения. Этот аналитический метод

проверки носит название верификация программ или доказательство корректности

программ. Верификация основана на систематическом применении правил вывода,

полученных в предыдущем параграфе. Проиллюстрируем этот прием на примерах

программирования на языке Visual Basic. Единственное отличие нотации данного

пункта, от ранее введенной – использование комментариев и оператора

присваивания этого языка.

Пример 1.

Алгоритм деления целых неотрицательных чисел x на у. Результат операции

частное q и остаток r, которые удовлетворяют соотношению

x=q*y+r ∧ 0≤r<y

Очевидно, это постусловие программы, ее предусловие имеет вид

x≥0 ∧ y>0

Алгоритм можно записать следующим образом

‘{x≥0

∧

y>0}

q = 0

r = x

‘{x=q*y+r

∧

0≤r}

While r>=y

‘{x=q*y+r ∧ 0≤y<r}

r = r-y

q = q-1

Wend

‘{x=q*y+r ∧ 0≤r<y}

Заметим, что первые два оператора q=0 и r=x автоматически гарантируют

истинность инварианта цикла {x=q*y+r ∧ 0≤r}. Этот типичный прием называется

инициализацией инвариантов цикла.

В примере 5 предыдущего параграфа мы доказали, что для цикла справедливо

правило

‘{(x=q*y+r) ∧ 0≤r}

While r>=y

r=r-y

q=1+q

Wend

‘{(x=q*y+r) ∧ 0≤r<y}

Так как программный составной оператор состоит из операторов инициализации

цикла и данного оператора цикла, то по правилу вывода для составного

оператора получаем постусловие программы {(x=q*y+r)∧0≤r<y}, что и требовалось

доказать.

Доказательство корректности программ хорошо сочетается с методом

проектирования программ сверху вниз. Он включает в себя следующие этапы:

1. Провести декомпозицию общей задачи на точно определенные подзадачи и

доказать, что если каждая задача решена корректно, и полученные решения

связаны между собой определенным образом, то первоначальная задача решена

корректно.

2. Повторить этот процесс "декомпозиции и доказательство корректности

декомпозиции" для подзадач.

3. Повторить этот процесс до достижения подзадач настолько простых, что их

решение может быть выражено в нескольких строках языка программирования.

Проиллюстрируем этот метод проектирования сверху вниз на простом примере.

Пример 2.

Умножение двух положительных целых чисел x и y. Результат – z.

Начальное описание алгоритма таково:

‘{x>0 ∧ y>0}

‘сложить значение у само с собой x раз

‘ {z=x*y}

Предусловие есть требование положительности х и у. Постусловие - результат

вычислений. Правильность преобразования предусловия в постусловие следует из

определения операции сложения.

Следующий уровень декомпозиции требует введения переменных z для хранения

промежуточной суммы и u, которая следит, сколько раз будет выполнено

сложение. Таким образом, получаем следующую декомпозицию:

‘{x>0 ∧ y>0}

Установить z равным нулю, u равным x

‘{z+u*y=x*y ∧ u>0}

‘Увеличить z на величину y и уменьшить u на 1; повторять этот процесс до тех

‘пор пока u не станет равным 0

{z=x*y}

Нетрудно заметить, что инвариантом является логическое выражение

z+u*y=x*y

Тогда подзадача 1 содержит операторы присваивания, инициализирующие этот

инвариант.

Действие «увеличить z на величину y и уменьшить u на 1» подзадачи 2

построено таким образом, чтобы сохранить инвариант. В самом деле,

Z+y+(u-1)*y=z+u*y=x*y

Условие «повторять этот процесс до тех пор, пока u не станет равным 0»,

гарантирует, что после окончания итераций будет получен требуемый результат

z=x*y.

Корректность подзадач показана, и мы получаем программу

‘{x>0

∧

y>0}

z = 0

u = x

z = z+y

u = u-1

Loop until u=0

‘{z=x*y}

Можно непосредственно доказать корректность этой программы.

До сих пор мы рассматривали только один аспект корректности программ, а

именно, являются ли корректными результаты, вырабатываемые в точке выхода,

если аргументы удовлетворяют входному утверждению. Другим не менее важным

аспектом корректности является требование, чтобы процесс приводил к

результатам после конечного числа шагов алгоритма.

Рассмотрим цикл While B S Wend. Пусть е является целочисленным

выражением.

Предположим, что

(1) P∧B ⇒ (e>0)

И для e

, принимающего целочисленные значения,

00 0

( ({0 } {0 }) (2)eeeSee∀<= ≤<

Это значит, что e≥0 также является инвариантом цикла. Кроме того, согласно

(2) каждое выполнение оператора S уменьшает значение е. При условии

выполнения (1), (2) и, полагая, что {P∧B} S {P} доказано, сразу можно сделать

вывод о конечности итерационного процесса, так как е не может уменьшаться

бесконечное число раз и оставаться положительным, как требует (1).

Пример 3.

Для цикла примера 1 в качестве функции е в соотношениях (1) и (2) следует

выбрать переменную r.

Для цикла do S loop until B требуется в дополнении к {P}S{Q} и Q∧¬B ⇒ P

необходимо доказать

(3) P ⇒ (e>0)

Тогда гарантируется завершаемость итерационного процесса за конечное число

шагов.

00 0

( ({0 } {0 }) (4)eeeSee∀<= ≤<

Пример 4.

Для цикла примера 2 в качестве функции е в соотношениях (3) и (4) следует

выбрать переменную u.

Разработка приложений в среде

Visual Basic 6.0

Введение

Visual Basic (Beginner’s All-purpose Symbolic Instruction Code)

представляет собой современную систему визуального программирования в среде

Windows.

Visual Basic является и интерпретатором, и компилятором. Как

интерпретатор, Visual Basic позволяет запускать приложения непосредственно в

среде разработки (команда Run\Start). Как компилятор, Visual Basic

предоставляет возможность создавать независимые от среды разработки

исполняемые ЕХЕ-файлы (команда File\Make имя_файла_проекта...).

Исторически различные приложения Microsoft включали различные языки

макросов, значительно отличающиеся друг от друга (WordBasic, ExcelMacro,

AccessBasic и т.д.). Начиная с Office 97, корпорация Microsoft стала снабжать

свои приложения общим языком макросов – VBA (Visual Basic for Applications).

Visual Basic for Applications является диалектом Visual Basic, учитывающим в

наборе используемых объектов и функций специфику приложений (текстовых

редакторов, электронных таблиц и т.п.). Поэтому Visual Basic широко

используется для разработки приложений под Windows на основе продуктов

Microsoft.

Имея длинную предысторию, язык Visual Basic обременен многими устаревшими

конструкциями, оставленными в языке для обратной совместимости с предыдущими

версиями. Поэтому ниже при описании синтаксиса указываются лишь рекомендуемые

конструкции. В качестве металингвистических символов используются квадратные

скобки для необязательных конструкций ([]), фигурные скобки для обязательных

конструкций ({}), вертикальная черта для разделения альтернативных

конструкций (|), многоточие для возможного повторения предшествующей

конструкции (...) и комбинация запятой с двумя точками для возможного

повторения предшествующей конструкции в виде списка конструкций, разделенных

запятой.

1. Интегрированная среда разработки

После запуска Visual Basic можно создать новый проект, указав его тип

(например, Standard EXE или VB Enterprise Edition Controls), загрузить уже

существующий проект или создать новый проект с помощью мастера (например,

мастера приложений VB Application Wizard). Приложение, созданное мастером,

можно в дальнейшем дорабатывать с помощью других штатных средств среды

разработки.

Главное окно интегрированной среды разработки (IDE - Integrated

Development Environment) содержит строку меню (Menu Bar), панели и окна.

Контекстное меню (Context Menu), как обычно, открывается щелчком правой

кнопки мышки.

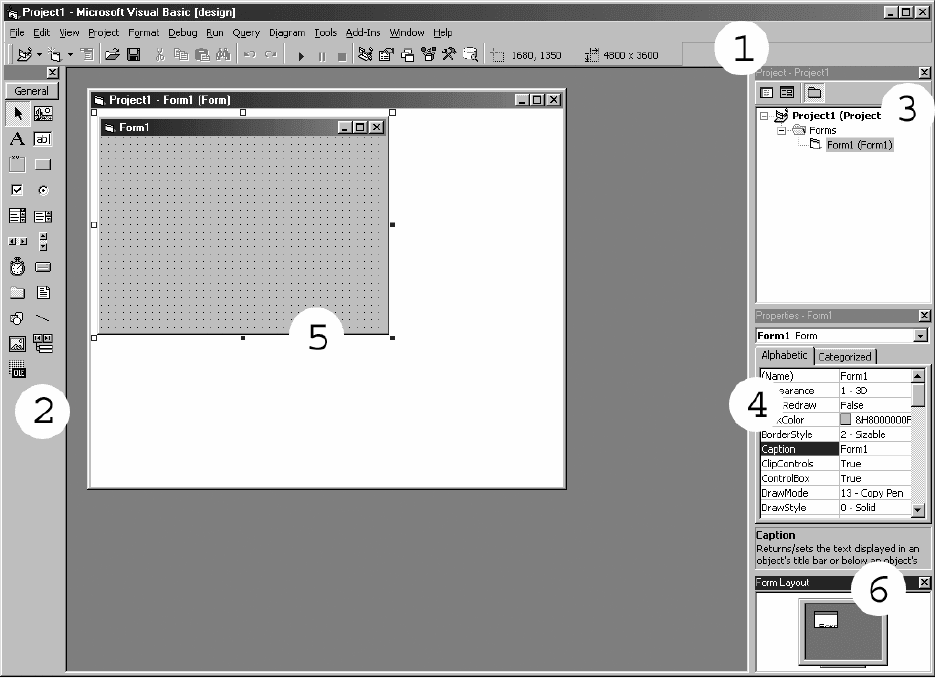
Toolbars - Панели инструментов (1)

Открывать и настраивать панели инструментов Debug (Отладка), Edit

(Правка), Form Editor (Редактор форм), Standard (Стандарт), а также Shortcut

Menus (Сокращенные меню) можно с помощью команды View \ Toolbars ►.

Toolbox - Панель элементов управления (2)

Панель содержит элементы управления, предназначенные для размещения на

формах. Комплект содержащихся на панели элементов зависит от типа проекта.

Открыть панель можно с помощью команды View \ Toolbox, настроить – с помощью

контекстного меню (команды Components…, Add Tab…) и с помощью перетаскивания

элементов между различными вкладками.

Project Explorer Window - Окно проекта (3)

Приложение в Visual Basic реализуется в виде совокупности файлов,

соответствующих различным компонентам проекта – формам, модулям, классам и

другим, перечисленным в меню Project \ Add тип_компонента_проекта. Информация

о файлах компонентов сохраняется в VBP-файле проекта. Если несколько проектов

объединяются в группу, их имена сохраняются в файле с расширением .VBG. Одни

и те же файлы компонентов могут быть использованы в различных проектах.

Открыть окно проекта можно с помощью команды View \ Project Explorer,

добавить новый компонент в проект - с помощью команды Project \ Add

тип_компонента_проекта.

Для сохранения компонента проекта необходимо выделить его в окне проекта и

затем выполнить команду File \ Save имя_файла [As…], для исключения

компонента из проекта - выполнить команду Project \ Remove имя_файла; при

этом файл с диска удален не будет.

Для сохранения всего проекта совместно со всеми компонентами необходимо

выполнить команду File \ Save Project [As…]. Команда File \ Remove Project

закрывает проект, т.е. исключает проект из среды разработки; на диске все

файлы проекта сохраняются.