Амелин Р.В., Блинков Ю.А. и др. Основные понятия информатики

Подождите немного. Документ загружается.

yyx∨=∨

(

)

(

)

yzxyz

∧

∧=∧ ∧

(

)

(

)

yzxyz∨∨=∨∨

закон ассоциативности

xx∧=

xx∨=

закон идемпотентности

(

)

xy x∧∨=

(

)

xy x∨∧=

закон элиминации

(

)

(

)

(

)

yz xy xz∧∨=∧∨∧

(

)

(

)

(

)

yz xy xz∨∧=∨∧∨

Закон дистрибутивности

(

)

(

)

(

)

yxy¬∧ =¬∨¬

(

)

(

)

(

)

yxy¬∨ =¬∧¬

закон де Моргана

(

)

yyx∨∧¬=

(

)

yyx∧∨¬=

закон нейтрализации

Не все представленные законы в таблице являются независимыми. Таким

образом, их количество избыточно. Избыточность часто используют в

программировании, для улучшения читаемости программ и уменьшения ошибок.

Главным критерием, при построении связей между функциями вычислительной

структуры, должна быть их полнота и непротиворечивость.

3.3. Вычислительная структура UINT

Зададим множество S типов и множество F символов функций вычислительной

структуры неотрицательных целых чисел UINT:

UINT = (S, F)

S = {bool, uint},

F = {true, false,

∧

∨

, zero, next, prev, +,-,*,\, mod ,

≤

≥

,<,>,=}

По построению UINT уже содержит внутри себя вычислительную структуру BOOL,

поскольку свойство упорядоченности одно из основных свойств целых чисел.

Такой подход при построении называют архитектурным или иерархическим.

Тип bool у нас уже описан. Множество носителей, сопоставленное типу uint

пусть состоит из следующих символов:

uint

UINT

= {0, 1, 2, ...}∪{ ⊥}.

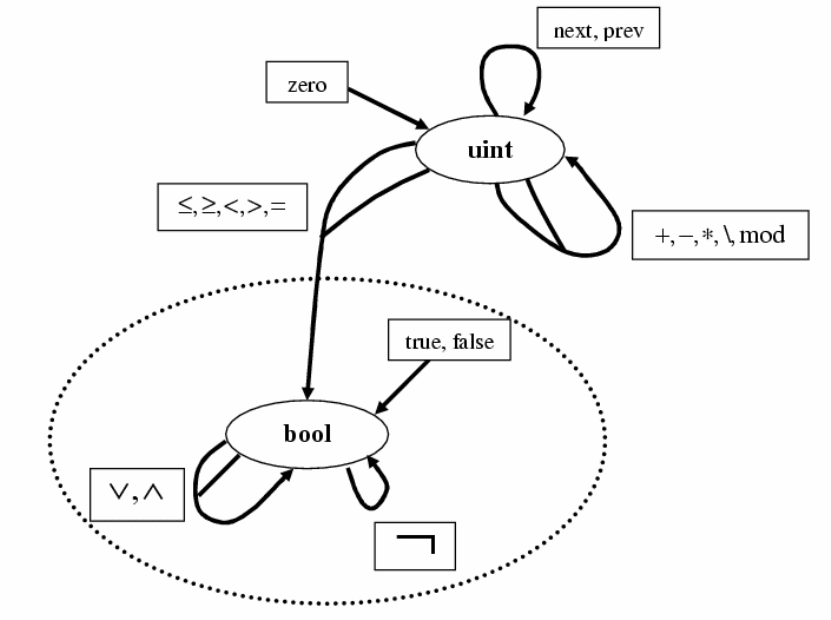
Для представления сигнатуры функций (задания типов входных и типа

выходного аргумента) воспользуемся диаграммой сигнатуры:

На представленном выше рисунке видно, что поскольку к типу bool от других

типов входит только одно входное ребро и, главное, нет ни одного выходного к

другим типам, он может быть выделен в отдельную вычислительную структуру.

Нульместная функция zero возвращает ноль. Функции next, prev возвращают

соответственно следующие и предыдущие значение входного аргумента. Операции

+,-,*,\,mod являются обычным сложением, вычитанием, умножением, целочисленным

делением и взятием остатка от деления. Опишем связи между функциями связанные

с типом uint, поскольку тип bool описан в вычислительной структуре BOOL. При

описании связей между функциями будем использовать дополнительное логическое

условие применения данного правила. Оно будет записываться, если необходимо,

в квадратных скобках за равенством.

∀ x, y ∈ uint

UINT

выполнены следующие равенства:

0zero

()

rev zero

⊥,

(())

rev next x x

zero x

= ,

() ( )

next y next x y

=+,

[

]

yxy

−

=⊥ < ,

zero x

−

= ,

[

]

() ( )

next y prev x y x y−=−≥,

zero zero

*()*

next y x y x

zero

⊥,

[

]

yzeroxy

< ,

[

]

\(()\)

y next x y y x y

−≥,

mod

zero

⊥ ,

[

]

mod

yxxy

< ,

(

)

[

]

mod mod

yxy yxy

−≥,

zero x true

≤

= ,

() ()next x next y x y

≤

=≤,

yyx≥=≤

(

)

yyx

=¬ ≤ ,

(

)

yxy>=¬ ≤ ,

()()

UINT

yxy yx

=≤∧≤

В последнем равенстве, поскольку равенство (=) употреблялось в различном

смысле (контексте), для устранения неоднозначности было использовано «полное

имя» функции =

UINT

. Очень важно сразу научиться обращать внимание на контекст.

В программировании всегда стоит дилемма: использовать полное описание и в

результате получить громоздкую программу или использовать контекст, и давать

полные имена только, когда это необходимо для устранения неоднозначности.

Как и при описании вычислительной структуры BOOL набор правил является

избыточным. Главное чтобы он был полным, т.е. любое соотношение между

функциями являлось комбинацией представленных. Надо также стремиться не

делать данный набор слишком большим. Для контроля за ошибками (в данном

случае это отсутствие полноты) удобно использовать лексикографический

порядок. Выше мы считали операцию next старше prev, и все правила

использовали именно эту операцию, хотя с помощью prev(next(x))=x они могли бы

быть переписаны и через prev. Аналогично поступили с операциями сравнения.

Полностью описав ≤, и считая её старшей, все остальные связи для функций

сравнения мы показали через нее и операции вычислительной структуры BOOL.

3.3. Вычислительная структура INT

В силу важности целых чисел для программирования рассмотрим вычислительную

структуру INT:

UINT = (S, F)

S = {bool, int},

F = {true, false,

∧

∨

, zero, next, prev, +,-,*,\, mod ,

≤

≥

,<,>,=}

Множество носителей, сопоставленное типу int, пусть состоит из следующих

символов:

int

INT

= {...,-1, 0, 1,...}∪{ ⊥}.

Для представления сигнатуры функций (задания типов входных и типа

выходного аргумента) воспользуемся диаграммой сигнатуры построенной для

вычислительной структуры UINT, заменив формально тип uint на int. Это пример

когда сигнатуры совпадают для различных вычислительных структур, хотя набор

связей между функциями может значительно различаться.

∀ x, y ∈ int

INT

выполнены следующие равенства:

0zero

(())

rev next x x

zero x

= ,

[

]

() ( ) 0x next y next x y y+=+≥,

[

]

0xyxyy

=− < ,

zero x

−

= ,

[

]

() ( ) 0x next y prev x y y−=−≥,

[

]

0xyxyy

−

=+ < ,

zero zero

[

]

*()* 0x next y x y x y

+≥

[

]

*()* 0xprevy xyx y

−≤

zero

⊥,

[

]

\(0)(0)x y zero x x y y x x= ≤∧< ∨ <∧≤ ,

[

]

\(()\)( 0)( 0)x y next x y y x y y x y y=− ≥∧>∨≤∧<,

[

]

\ (( )\)(0 0)(0 0)xy prevx y y x y x y= + ≥∧< ∨ ≤∧> ,

mod

zero

⊥ ,

[

]

mod (0 ) ( 0)xyx xxyyxx= ≤∧< ∨ <∧≤ ,

[

]

mod (( ) mod ) ( 0) ( 0)x y next x y y x y y x y y=− ≥∧>∨≤∧<,

[

]

mod (( ) mod ) ( 0 0) ( 0 0)xyprevxy yx y x y=+ ≥∧<∨≤∧>,

() ()next x next y x y

≤

=≤,

yyx≥=≤,

(

)

yyx

=¬ ≤ ,

(

)

yxy>=¬ ≤ ,

()()

INT

yxy yx

=≤∧≤.

При написании связей между функциями, в отличие от вычислительной

структуры UINT, положен принцип симметрии. Введение дополнительных правил,

если имеется произвол при написании, позволяет избежать ошибок и опечаток.

Этот принцип очень часто используется в различных аспектах программирования.

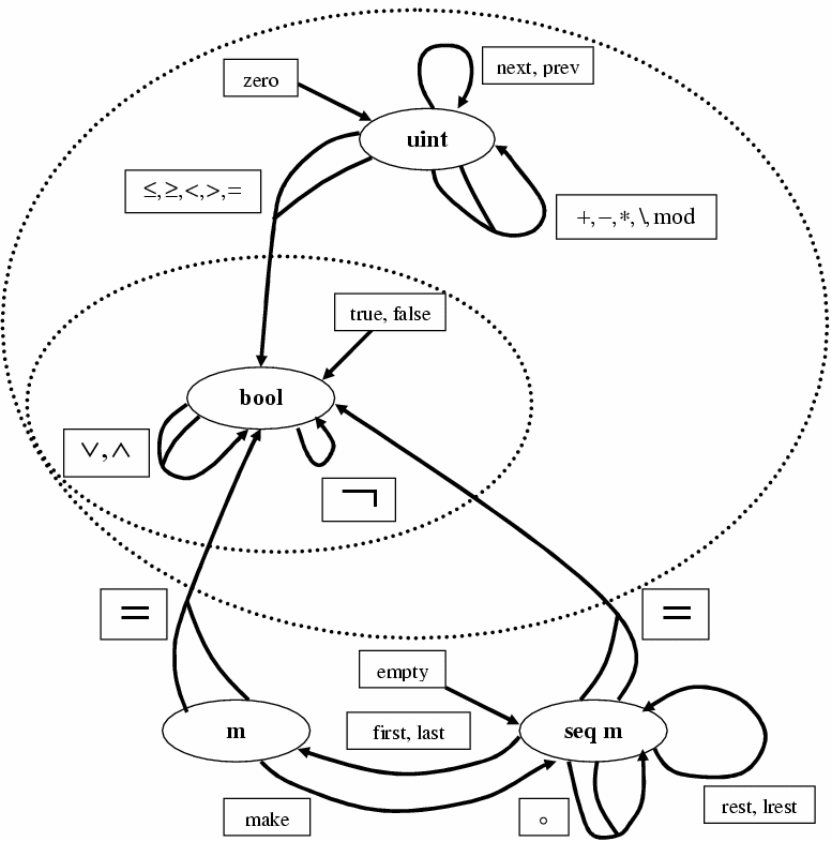
3.4. Вычислительная структура SEQ

Одной из вычислительных структур, в явном или неявном виде используемой в

различных языках программирования, служит понятие последовательности. При ее

формулировке сразу возникает проблема параметризации. Поскольку

последовательности могут образовывать элементы любого типа, будем

рассматривать вычислительную структуру SEQ с типом m в качестве параметра:

SEQ m = (S, F)

S = {bool, uint, m, seq m}

F = {true, false,

∧

∨

, zero, next, prev, +,-,*,\, mod ,

≤

≥

,<,>,=

UINT

empty, make, o, first, last, rest, lrest, length, =

SEQ m

}

SEQ m содержит в качестве типов вычислительные структуры BOOL и UINT.

Множество носителей, сопоставленное типу seq m, пусть состоит из следующих

символов:

seq m

SEQ m

= {m}*∪{⊥}.

Представленные на диаграмме функции выполняют следующие действия:

empty конструирует пустую последовательность. make создает

последовательность из одного элемента. Операция o сливает последовательности.

first возвращает первый элемент, а last последний. rest возвращает

последовательность без первого элемента, а lrest соответственно без

последнего. lenght дает количество элементов последовательности. =

сравнивает

элементы последовательности, а =

SEQ m

— сами последовательности.

∀ x ∈ m

SEQ m

и ∀ y, z ∈ seq m

SEQ m

выполнены следующие равенства:

empty

<>,

()make x x

<>,

yempty y

o ,

yz zy

oo,

()

irst empty

⊥,

(())

irst make x y x

o ,

()last empty

⊥ ,

(())last y make x x

o ,

()rest empty

⊥ ,

(())rest make x y y

o ,

()lrest empty

⊥,

(())lrest y make x y

o ,

()0length empty

(()) ( ())length make x y next length y

o ,

SEQ m

empty empty true

= ,

[

]

()

SEQ m

y empty false y empty==¬=,

[

]

()

SEQ m

empty z false z empty== ¬= ,

[]

(() ())(() ())

()()

SEQ m m SEQ m

y z first y first z rest y rest z

y empty z empty

== = ∧ =

¬= ∧¬=

3.4. Вычислительная структура SET

Одна из вычислительных структур может использоваться для имитации другой

вычислительной структуры. Данный подход часто используется в

программировании. Таким образом поступают при моделировании разнообразных

данных возникающих в задачах с помощью ограниченного набора базовых типов,

которые поддерживаются архитектурой компьютера. Рассмотрим одну из основных

структур математики — вычислительную структуру множества SET с элементами

типа m, смоделированную SEQ m:

SET m = (S, F)

S = {bool, uint, m, seq m}

F = {true, false,

∧

∨

, zero, next, prev, +,-,*,\, mod ,

≤

≥

,<,>,=

UINT

empty, make, o, first, last, rest, lrest, length, =

SEQ m

∅

, {},

∈

∪

∩

⊂

⊆

, Card, =

SET m

}

SET m содержит в качестве типов вычислительные структуры BOOL, UINT и SEQ m.

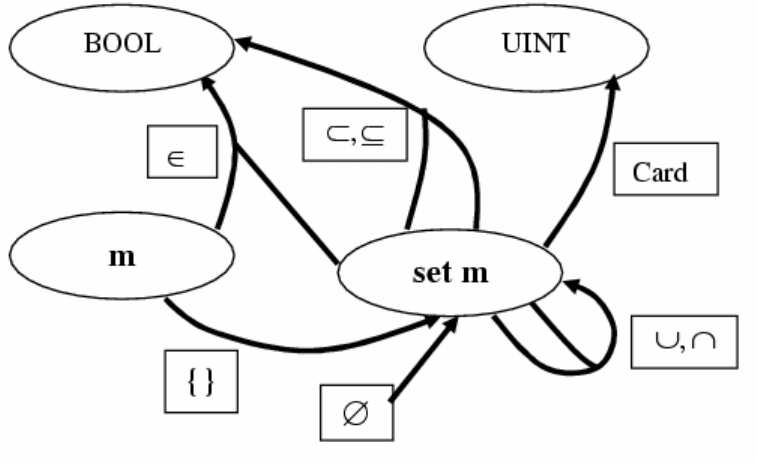
При построении диаграммы сигнатур не будем изображать структуры BOOL и

UINT подробно, заменив их овалами. Тип seq m будет заменен типом set m:

Связи между функциями определим через функции seq m.

∀ x ∈ m

SET m

и ∀ y, z ∈ seq m

SET m

выполнены следующие равенства:

empty

∅

= ,

{} ( )

make x

false

∈

∅= ,

[

]

( ( )) ( ( )) ( )

y x first y x rest y y empty

∈

== ∨∈ ¬= ,

yy∪∅= ,

[

]

( ( )) ( ( )) ( ( ) )y z make first z y rest z first z y∪= ∪ ¬ ∈o ,

[

]

() ()y z y rest z first z y∪=∪ ∈ ,

yempty

∩

∅= ,

[

]

() ( () )y z y rest z first z y∩=∩ ¬ ∈ ,

[

]

( ( )) ( ( )) ( )y z make first z y rest z first z y∩= ∩ ∈o ,

ztrue

∅

⊆= ,

[

]

(())(())( )y z first y z rest y z y empty⊆= ∈ ∧ ⊆ ¬ = ,

()()

SET m

yzyzzy

=⊆∧⊆,

()( )

SET m

yz yz y z⊂= ⊆ ∧¬ = ,

() ()Card y length y

3.5. Вычислительная структура FILE

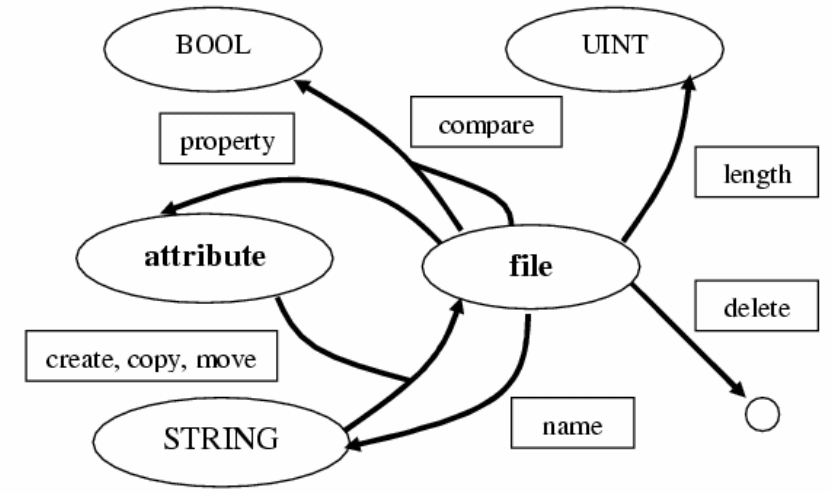
Вычислительные структуры не обязательно представляют математические

объекты или типы данных языков программирования. Они могут моделировать

всевозможные редакторы, окна Windows, калькуляторы и т.д. Рассмотрим в

качестве характерного примера вычислительную структуру FILE.

Для демонстрации приведем диаграмму сигнатур и краткое описание функций и

типов данных. В реальных операционных системах вычислительная структура

FILE

значительно сложнее.

Тип attribute используется при создании (create), копировании (copy),

переносе (move). Тип attribute сильно зависит от операционный системы. Обычно

это множество состоит из следующих свойств (property): скрытый, системный,

только для чтения и т.д. Вычислительная структура строк STRING представляет

набор всевозможных операций со строками и представляет собой

специализированное свойство типа file. Аналогичным специализированным

свойством выступает размер файла. Его предоставляет функция length.

Содержимое файлов может быть сравнено с помощью функции compare. При удалении

(delete) файла он перестает существовать. Для обозначения в этом случае, того

что функция не возвращает значения, использовался пустой круг.

4. Языки программирования высокого уровня

4.1. Синтаксис, формальные грамматики.

Для представления алгоритмов, предназначенных для выполнения на ЭВМ,

используются языки программирования (ЯП). Внешняя форма программы на ЯП

устанавливается с помощью синтаксиса языка , который определяет формальный

язык. Он определяется с помощью определенных грамматических правил,

аналогичных алгоритму текстовых подстановок. Основой формального определения

синтаксиса являются формальные грамматики.

Синтаксис языка — это набор правил, определяющих допустимые конструкции

языка. Синтаксис определяет «форму языка» — задает набор цепочек символов,

которые принадлежат языку.

Семантика языка — это раздел языка, определяющий значение предложений

языка. Семантика определяет «содержание языка» — задает смысловое значение

для всех допустимых цепочек языка.

Грамматика — это описание способа построения предложений некоторого языка.

Иными словами, грамматика — это математическая система, определяющая язык.

Грамматику языка можно описать различными способами: например, грамматика

русского языка описывается довольно сложным набором правил.

Правило — это упорядоченная пара цепочек символов (α, β). В правилах очень

важен порядок цепочек, поэтому их чаще записывают в виде α→β.

Формально грамматика G определяется как четверка (N, T, P, S), где

• N — конечное множество нетерминальных символов или нетерминалов;

• T — конечное множество терминальных символов или терминалов, причем

N∩T=∅;

• P — конечное множество правил грамматики вида α→β,

где (α , β) ∈

***

()()()NTNNT NT×UUU

• S — символ из N, называемый начальным символом.

Множество V = N∪T называют полным алфавитом грамматики G.

Каждый символ множества N может встречаться в цепочках как левой, так и

правой частей правил грамматики, но он обязан хотя бы один раз быть в левой

части хотя бы одного правила. Правила грамматики строятся так, чтобы в левой

части каждого правила был хотя бы один нетерминальный символ.

Пример 1.

Дана грамматика G =({A, S}, {0, 1}, P, S), где P = {S→0A1, 0A→00A1, A→e}.

Нетерминальными символами являются A, S, а терминальными 0, 1.

Грамматика определяет язык рекурсивным образом посредством задания особого

рода выводимых цепочек.

Выводимые цепочки грамматики G = (N, T, P, S) определяются следующим

образом:

• S — выводимая цепочка;

• Если αβγ — выводимая цепочка, и β→δ содержится в Р,

то αδγ - тоже выводимая цепочка

Выводимая цепочка грамматики G, не содержащая нетерминальных символов,

называется терминальной цепочкой, порождаемой грамматикой G.

Язык, порождаемый грамматикой G (L(G)) - это множество терминальных

цепочек, порождаемых грамматикой G.

Пусть G = (N, T, P, S) — грамматика, V = N∪T — ее алфавит. α,β,γ ∈ V*, δ ∈

. Цепочка ϕ = αβγ называется непосредственно выводимой из ψ = αδγ в

грамматике G, если в G существует правило δ→β ∈ P. Обозначается ψ ⇒

ϕ. В

тех случаях, когда из контекста ясно, о какой грамматике идет речь, нижний

индекс G будем опускать.

Иными словами, цепочка ϕ непосредственно выводима из ψ, если можно взять

несколько символов в цепочке ψ, заменить их на другие символы согласно

правилу грамматики и получить цепочку ϕ. Любая из цепочек δ и β (или обе они)

может быть пустой. В предельном случае вся цепочка ψ может быть заменена на

цепочку ϕ, тогда в грамматике G должно существовать правило ψ→ϕ ∈ P.

Через ⇒

будем обозначать k-ю степень отношения ⇒. Иначе говоря, α⇒

β ,

если существует последовательность α

,α

, α

,…, α

, состоящая из k+1 не

обязательно различных цепочек, для которых α=α

, α

i-1

⇒α

, 1≤i≤k и α

=β. Эта

последовательность называется выводом длины k цепочки β из цепочки α в

грамматике G.

Введем отношение ϕ⇒

ψ означающее, что цепочка ψ выводима из ϕ

нетривиальным образом: ϕ⇒

ψ тогда и только тогда, когда ϕ⇒

ψ для некоторого

i≥1.

Говорят, что цепочка ψ выводима из ϕ (обозначение ϕ⇒

ψ)тогда и только

тогда, когда ϕ⇒

ψ для некоторого i≥0.

Вывод называется законченным, если на основе цепочки ϕ, полученной в

результате вывода, нельзя больше сделать ни одного шага вывода. Иначе говоря,

вывод называется законченным, если цепочка ϕ пустая или содержит только

терминальные символы грамматики G = (N, T, P, S). Цепочка, полученная в

результате законченного вывода, называется конечной цепочкой вывода.

Грамматики можно классифицировать по виду их правил.

Грамматика G = (N, T, P, S) называется

• праволинейной, если каждое правило из Р имеет вид A→αB или A→α, где

A,B∈N, α∈V*;

• контекстно-свободной (бесконтекстной), если каждое правило из Р имеет

вид A→α, где A∈N, α∈V*;

• контекстно-зависимой (неукорачивающей), если каждое правило из Р имеет

вид α→β, где α≤β.

Грамматика, не удовлетворяющая ни одному из указанных ограничений,

называется грамматикой общего вида или грамматикой без ограничений.

Пример 2.

Праволинейная грамматика G

=({S}, {0, 1}, {S→0S|1S|e},S) порождает язык

L(G

)={0,1}*.

Пример 3.

Пусть G

=({E, T, F}, {a, +, *, (, )}, P, E), где Р состоит из правил

E→E+T|T

T→T*F|F

F→(E)|a

Язык L(G

) представляет собой множество арифметических выражений,

построенных из символов a, +, *, (, ). Грамматика G

— контекстно-свободная.

Пример 4.

Пусть G

=({C, B, S}, {a, b, c}, P, S), где Р состоит из правил

S→aSBC|abC

CB→BC

bB→bb

bC→bc

cC→cc

Эта грамматика порождает язык {a

| n≥1}.Очевидно, это контекстно-

зависимая грамматика.

Для записи синтаксиса конструкций языков программирования часто используют

форму Бэкуса-Наура. Она практически ничем не отличается от нотаций продукций

формальных грамматик, только вместо знака → используется обозначение ::=.

Пример 5. Десятичное целое без знака.

<Десятичное_целое_без_знака>::=<Цифра>|<Десятичное_целое_без_знака><Цифра>

<Цифра>::=0|1|2|3|4|5|6|7|8|9

4.2. Семантика.