Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH010.tex 10/9/2010 15: 22 Page 406

406 Computational Fluid Dynamics and Heat Transfer

By substituting equation (59) into equation (58), the following expression,

which is used to adjust the values of the nor malization constant of the smoothing

function, n

, yields:

1.0

F(s,h)dη



(60)

Equation (60) is essentially equivalent to the corrective interpolation for mulation

for a ﬁeld quantity of zero-th order proposed by Liu et al. [15], which gives for the

1-D 3-spline quintic kernel, n

[39]

120

⎧

⎪

⎨

⎪

⎩

1.4632 1st closest particle to the boundary

1.0781 2nd closest particle to the boundary

1.0054 3rd closest particle to the boundary

1.0 other particles

(61)

The particle closest to the boundary gets the largest modiﬁcation factor, 1.4632,

which implies that the “near-boundary deﬁciency” stays primarily with the closest

particle to the boundary.

10.4.4 Results

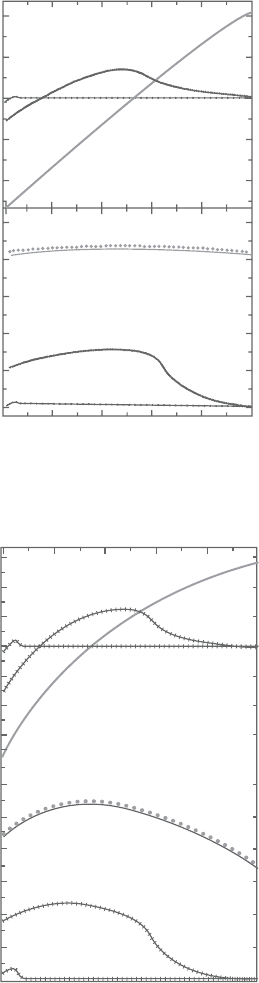
Figures 10.10 and 10.11 display the non-dimensional diffusive temperature and

heat ﬂux distributions in thin ﬁlms of different thicknesses yielding for Kn values

of 10 and 1.0, respectively. The overall agreement between the SPH and FDM

calculationsis excellentand moreaccuratepredictionscanbegiven by SPHforthe

heat conduction processes in solid ﬁlms with smaller values of Kn.

The distributions for the total (summation of the ballistic and diffusive com-

ponents) temperature and heat ﬂux were also calculated; the ballistic component

dominatesandduetoitsanalyticalformulationyieldsenhancedagreementbetween

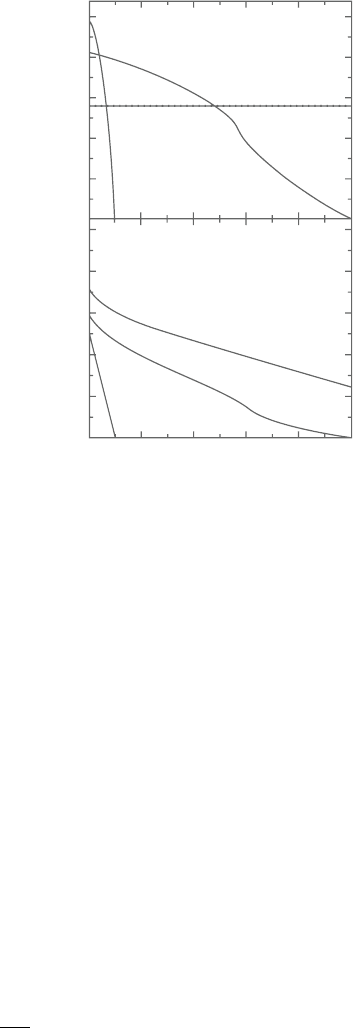
the SPH and FDM results, as shown in Figure 10.12.

As seen from Figure 10.12, the calculated boundary temperature is not con-

stant, but increases as time advances. In Chen [31] this artiﬁcial temperature

jump is attributed to the inconsistency between the temperatures obtained in the

ballistic-diffusive calculation and the imposed boundary temperature. As men-

tioned previously, the imposed boundary temperature is the temperature of the

emitted phonon, not the equivalent equilibrium temperature at the boundary; how-

ever, the calculatedtemperature isthe temperatureof equilibrium phononsthat can

be understood as a measure of the local internal energy. The so-called equivalent

equilibrium concept can be visualized as the adiabatic thermalization equilibrium

state of the local phonons. In what concerns the SPH calculation, the temperature

ofthe particle closestto theboundarycannotbedetermineddirectlyfrom thespec-

iﬁed temperature of the emitted phonons at the boundary, but depends on the SPH

smoothing interpolation. This fact explains why further treatment of the boundary

Sunden CH010.tex 10/9/2010 15: 22 Page 407

SPH – a versatile multiphysics modeling tool 407

Kn = 1.0

Lines : FDM

Symbols : SPH

* ⫽ 0.1

* ⫽ 0.01

* ⫽ 1.0

Non-dimensional position

Non-dimensional diffusive

temperature

Non-dimensional diffusive

heat flux

0.0

0.01

0.02

0.03

0.04

0.05

−0.02

−0.01

0.00

0.01

0.02

0.2 0.4 0.6 0.8 1.0

* ⫽ 0.1

* ⫽ 0.01

* ⫽ 1.0

Figure 10.10. Comparison between the SPH and the FD predictions for non-

dimensional diffusive temperature and heat ﬂux with Kn=10.

Kn ⫽ 1.0

Lines : FDM

Symbols : SPH

t * ⫽ 0.1

t * ⫽ 10

Non-dimensional diffusive

temperature

Non-dimensional diffusive

heat flux

Non-dimensional position

0.0

0.00

0.05

0.15

0.25

−0.12

−0.09

−0.06

−0.03

−0.00

0.03

0.06

0.09

0.10

0.20

0.30

0.2 0.4 0.6 0.8 1.0

Figure 10.11. Comparison between the SPH and the FD predictions for non-

dimensional diffusive temperature and heat ﬂux with Kn=1.0.

Sunden CH010.tex 10/9/2010 15: 22 Page 408

408 Computational Fluid Dynamics and Heat Transfer

Kn ⫽ 1.0

Lines : FDM

Symbols : SPH

t * ⫽ 1.0

Non-dimensional position

Non-dimensional temperature Non-dimensional heat flux

0.0

0.2

0.4

0.6

0.8

1.0

0.00

0.05

0.10

0.15

0.20

0.25

0.2 0.4 0.6 0.8 1.0

t * ⫽ 1.0

t * ⫽ 10

Figure 10.12. Comparison between the SPH and the FD predictions for non-

dimensional total temperature and heat ﬂux with Kn=1.0.

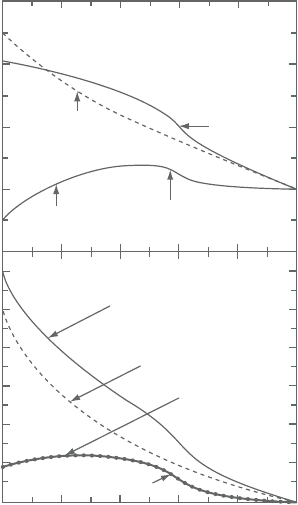
is required. Figure 10.13 displays the contributions of the ballistic and diffusive

components to the total temperature (internal energy) and heat ﬂux. The SPH cal-

culations reproduce the characteristics of the ballistic-diffusive heat conduction

reported in Chen [31].

Close observation of the calculation source data for all the 500 SPH particles

reveals an anomaly for the SPH heat ﬂux result for the second particle away from

the boundary. The heat ﬂux of this particle is inconsistent with the overall trend of

the heat ﬂux proﬁle and clearly deviates from the FDM predictions. This par ticle

was not shown in Figure 10.10 due to the limited amount of particles (only 50)

selected.The implementation of equation (61) can affect the symmetry of the SPH

formations, in particular that given by equation (55), which may explain the cause

forthisanomaly.Atestsimulationdemonstratesapossibleremedyforthisanomaly

is the use of a ad hoc operation: artiﬁcially increase the n

of the second par ticle

close to the boundary to 1.234 (mid value of the n

-s for the ﬁrst and third particle

away from the boundary), which yields [39]

120

⎧

⎪

⎨

⎪

⎩

1.4632 1st closest particle to the boundary

1.234 2nd closest particle to the boundary

1.0054 3rd closest particle to the boundary

1.0 other particles

(62)

Sunden CH010.tex 10/9/2010 15: 22 Page 409

SPH – a versatile multiphysics modeling tool 409

Kn ⫽ 1.0, t ⫽ 1.0

Solid Lines : FDM

Symbols : SPH

0.0

Non-dimensional temperature

Non-dimensional position

Artificial wave front

Diffusive

component

Diffusive

component

Ballistic component

Ballistic

component

Total

Non-dimensional heat flux

0.1

0.2

0.3

0.4

0.5

0.6

−0.1

0.0

0.1

0.2

0.3

0.2 0.4 0.6 0.8 1.0

Figure 10.13. Contribution of the ballistic and diffusive components to the non-

dimensional total temperature and heat ﬂux.

Increasing the n

valueof the second closest particle to the boundary improves the

symmetry contributions amongthe particles in thevicinity of theboundary region,

in particular the symmetry between the ﬁrst and second closest particles to the

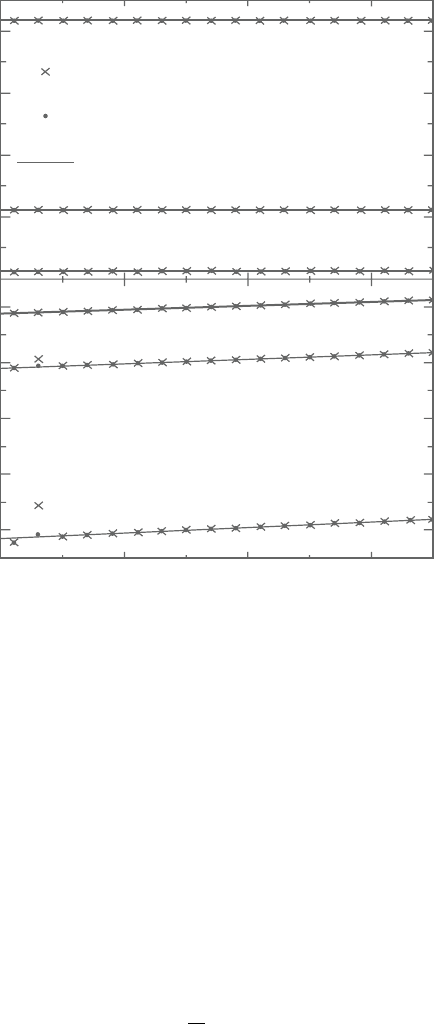
boundary. By plotting all the SPH particles near the left boundary, Figure 10.14

clearly indicates the limitation of the treatment formulated by equation (61).

The use of equation (62) provides an effective ad hoc modiﬁcation for the n

byeliminating the observed heat ﬂux anomaly and it does not inﬂuence the overall

calculation accuracy.

10.5 Mesoscopic Pore-Scale SPH Model for Fluid Flow

in Porous Media

Manyindustrial applications involve ﬂow inporousmedia, such as oilexploration,

groundwater puriﬁcation from hazardous wastes, and packed bed chemical reac-

tors. One application area of particular interest is in liquid composite molding

Sunden CH010.tex 10/9/2010 15: 22 Page 410

410 Computational Fluid Dynamics and Heat Transfer

0.04

Kn = 10

SPH with boundary treatment

expressed by eqation (61)

SPH with boundary treatment

expressed by eqation (62)

FDM

t * = 1.0

t * = 0.1

t * = 1.0

t * = 0.01

0.03

0.02

0.01

0.00

0.000

−0.005

−0.010

−0.015

−0.020

0.000

Non-dimensional diffusive

heat flux

Non-dimensional diffusive

temperature

0.010 0.020

Non-dimensional position

0.030

Figure 10.14. Error resulting from the boundary treatment expressed by equa-

tion (61) and the ad hoc correction effect by using equation (62).

(LCM), a process being widely used to manufacture polymer composite compo-

nents in the civil, aerospace, automotive and defense industries [40]. Important

LCMtechnologiesare theresin transfermolding (RTM)and thestructuralreaction

injection molding (SRIM), and for both cases the understanding of the physics of

liquid ﬂow in the porous preform is a requirement for the design of the mold and

the choice of the operation procedure, which are critical to the quality of the ﬁnal

product. To this goal CFD numerical modeling can effectively reduce the experi-

mental parametric investigation effort needed for the optimization of the industrial

process.Therefore,it canplayanimportant rolein practice.CFD modelingof ﬂuid

ﬂow in porous media is in general conducted by using Darcy’s law [41, 42], which

is expressed in the following form:

v=−

∇P (63)

Sunden CH010.tex 10/9/2010 15: 22 Page 411

SPH – a versatile multiphysics modeling tool 411

where, <v> and P are the volume averaged (superﬁcial) velocity and the pressure

of the ﬂuid (bold text denotes vector or tensor); K is the permeability tensor of the

porous medium; and µ is the dynamic viscosity of the ﬂuid.

Darcy’s law is a macroscopic phenomenological model, which is largely based

on experimental observations. In this law, the complex interactions between ﬂuid

and microscopic porous structures are all lumped in a macroscopic physical

quantity – the permeability tensor, K. As the permeability tensor is of paramount

importance to the ﬂuid ﬂow in porous media, numerous research efforts [42–45]

were devoted to establish theoretical relations between the permeability and other

characteristic material properties with the purpose of avoiding time-consuming

physical experiments.These theoreticalmodels are generally based on the analysis

of the microscopic porous structure of the medium and the subsequent extraction

of the desired macroscopic information. The complicated, diverse pore structures

in reality present a major challenge to pure (or semiempirical) theoretical models

because they are all constructed on the basis of artiﬁcially simple, regular pore

arrangements.

Obviously, the modeling of ﬂuid ﬂow in ﬁbrous porous media directly from

the mesoscopic pore structure level provides reﬁned ﬂuid ﬂow information and

it does not resort to Darcy’s law. Moreover, the simulated ﬂuid ﬁeld is amenable

to the determination of K as well. Over the last few decades, rapid advances in

computer capabilities andcomputational algorithms enabled thiskind of modeling

work. For example, the lattice-gas-automaton (LGA) or lattice Boltzmann method

(LBM) [46], based upon a micro- or mesoscopic model of kinetic formulations

or the Boltzmann equation, respectively, can bridge the gap between microscopic

structuresandmacroscopicphenomena.Thesemodelshavetheadvantageofallow-

ing parallelism in a straightforward manner for large-scale numerical calculations,

and they have the attractive feature of nonslip bounce-back solid boundar y treat-

ment for the simulation of ﬂuid ﬂow in porous media. The simulations based on

LGA [47, 48] and LBM [49–51] have demonstrated that Darcy’s law can be repro-

duced by these methods. The simulated porous media in the work by Koponen et

al. [49] describe three-dimensional (3-D) random ﬁber webs that closely resemble

ﬁbrous sheetssuch as paper andnon-woven fabrics.The computed permeability of

these webs presents an exponential dependence on the porosity over a large range

of porosity and is in good agreement with experimental data [52, 53]. Spaid and

Phelan [51] investigated the resin injection process encountered in RTM. The cell

permeability obtained for transverse ﬂow through regularly arranged porous tows

of circular or elliptical cross-section agrees well with the semi-analytical solution.

In contrast to LBM or LGA, SPH is a meshless particle-based method and offers

more freedomin dealingwith complicated geometries.Application of SPHto ﬂuid

ﬂow in porous media has the potential of providing a mesoscopic/microscopic

pore-scale insight into the relevant physics [54–57]. In the present work, SPH

is employed to construct a mesoscopic pore-scale model for ﬂuid ﬂow in porous

media,inparticular,forthetransverseﬂuidﬂowinrandomlyalignedﬁbrousporous

media.

Sunden CH010.tex 10/9/2010 15: 22 Page 412

412 Computational Fluid Dynamics and Heat Transfer

10.5.1 Modeling strategy

SPH formulation and methodology

SPH formulation is directly based on the resolution of the macroscopic governing

equationsofﬂuidﬂow.DerivationoftheSPHformulationfromtraditionalEulerian-

based equations is routine, as described in Section 2; therefore, in this section is

only brieﬂy surveyed.

InSPH,thecontinuousﬂowattimet isrepresentedbyacollectionofN particles

located at position r

(t) and moving with velocity v

(t), i=1,2,......,N. The

“smoothed” value of any ﬁeld quantity q(r, t) at a space point r is a weighted sum

of all contributions from the neighboring particles

q(r,t)=



j=1

ρ(r

)

q(r

,t)w(|r −r

|,h) (64)

where,m

andρ(r

)denotethe massand densityof particle j, respectively.w(|r|,h)

is the weight or smoothing function with h being the smoothing length. In the

present SPH implementation, the high-order 3-splines quintic kernel [15] is used

andthesmoothinglengthh isequalto

√

2S,withS beingtheaverageseparation

oftheSPHparticles.IntheSPHformulationthegradientofq(r,t)isdeterminedas:

∇q(r,t)=



j=1

[q(r

,t) −q(r,t)]∇w( |r − r

|,h) (65)

Equation (65) is already symmetrized [24], and for the second order viscous

diffusive term, the SPH theory gives the following formulation [8, 24]:

∇·(µ∇q) =



(µ

+ µ

∂w

∂r

(66)

where, q

−q

, r

−r

and w

=w(|r

−r

|,h).

In terms ofequation (65), the “smoothed”version ofthe continuity equationis:

dρ



· r

∂w

∂r

(67)

The summationis overall neighboring particles j with exceptionof particle n itself

and v

−v

The transformation of the N–S equations into their SPH version is relatively

involved,becauseitrequiresthesymmetrizationofthepressureterms[24]tosatisfy

momentumconservation, and theadequate treatmentofthe viscousterms. InSPH,

Sunden CH010.tex 10/9/2010 15: 22 Page 413

SPH – a versatile multiphysics modeling tool 413

the symmetrization version of pressure gradient can be formulated as:

∇p







∂w

∂r

(68)

Fromequations(66)and(68),thestandardSPHformofN–Sequationisderived[8]

=−









∂w

∂r





+ µ





∂w

∂r



(69)

where, F

denotes an external body force. In this work, the following SPH

expression for the momentum equations is used.

=−





+ RG



∂w

∂r

(70)



(µ

+ µ



∂w

∂r



+ F



Equation (70) was proposed by Jiang et al. (2007) and it differs from the standard

SPH N–S equation in what concerns two terms on the right-hand side of this equa-

tion, namely: (a) RG

, an artiﬁcial pressure, which is used to restrain the tensile

instability [58]; (b)



f , an additional force, which is introduced with the purpose

of correctly mimicking the no-penetrating restraint prescribed by the solid pore

structure. The ter m RG

is calculated as follows:

w(S,h)

(71)

R =

⎧

⎪

⎨

⎪

⎩

if p

< 0

if p

< 0





if p

> 0 and p

> 0

(72)

The factors ϕ

and ϕ

are taken to be 0.2 and 0.05, respectively. The exponential

η is dependent on the smoothing kernel as η ≥w(0,h)/w(S,h); 3.0 is adopted

for η in this work. The repulsive force f (per unit mass) is initiated from a porous

material particle and is applied to the neighboring ﬂuid particles within a distance

Sunden CH010.tex 10/9/2010 15: 22 Page 414

414 Computational Fluid Dynamics and Heat Transfer

less than a threshold value r

. In these conditions, for most of the ﬂuid particles,



f =0. f isassumedto beof the12-6 Lennard–Jones pairpotential form, namely

f (r) = φF







−







(r < r

) (73)

Determination of the constants: φ and r

were discussed in detail in Jiang et al.

[55]; the values r

=0.6S and φ =15.0 were found to be suitable for the present

SPH implementation.

The quasi-compressible method, presented in Section 2 is used to comply with

the incompressibility condition for the ﬂuid. The values of p

and c

are taken in

accordance with the following relation

γp

= max



0.01U

,0.01F

0.01Uµ



(74)

where, U and L are the characteristic (or maximum) ﬂuid velocity and the

characteristic length of the geometry, respectively.

Thepositions ofSPH particles aredetermineddirectlyfrom theﬂowﬁeld using

= v

(75)

Adirect numericalintegrationalgorithmisused toperform theintegrationofequa-

tions (67), (70), and (75). The time step t is adaptive and determined by the CFL

condition [8]

t = min

⎛

⎜

⎝

0.125h

max

(∼100.0U,|v

,0.25



0.25h

s,n

⎞

⎟

⎠

(76)

On the right-hand side of equation (76), the quantity ∼100.0U is introduced in

the denominator of the ﬁrst constraint to restrict it to a small value so that the

calculation advances mostly in a ﬁxed small time step. In this way the accuracy

of the integration procedure can be enhanced and the calculation stability is also

improved.

Mesoscopic pore structures

The porous matrix is established by randomly packing a certain number of ﬁbers.

Only the transverse ﬂow across the ﬁbers is simulated in the present implemen-

tation. Typical 2-D porous microstructures are illustrated in Figure 10.15. The

cross-sectional shape of the ﬁbers is either circular (Figure 10.15a) or square

(Figure 10.15b), and the ﬁbers can be either overlapped with no precondition-

ing (Figures 10.15a and b) or be isolated from each other (Figure 10.15c). Each

porous system is formed by packing ﬁbers of ﬁxed cross-section (shape and area).

Sunden CH010.tex 10/9/2010 15: 22 Page 415

SPH – a versatile multiphysics modeling tool 415

(c)

(a) (b)

Figure 10.15. Typical 2-D porous microstructures formed by randomly packing a

number of ﬁbers: (a) ﬁbers are of circular cross-section with unlim-

itedoverlappingbetweenﬁbers; (b)ﬁbersareofsquarecross-section

with unlimited overlapping between ﬁbers; (c) ﬁbers are of circular

cross-section and the ﬁbers are isolated from each other.Void space

represents the ﬂuid region.

Different porous systems have ﬁbers of different cross-sectional shapes, different

cross-sectional areas or different relative arrangement conditions.

BoththeresinﬂuidandtheﬁbersarerepresentedbySPHparticles.Thepositions

of the SPH particles used to represent the solid pore matrix are ﬁxed throughout

the simulation. Thus, the porosity ε of a porous system is determined as:

ε = 1 −

number of ﬁxed particles

total number of particles

(77)

Fixedporousmaterialparticlescontributetothedensityvariationsandexertviscous

forces upon the nearby ﬂuid particles, while their densities are kept constant. The

no-penetrating restraint prescribed by solid pore structure is ensured by activating

a repulsive force, as expressed by equation (73), on a ﬂuid particle once it is away

fromaporousmaterialparticlebyadistancelessthanr

.Withthisadditionalforce,

theﬂuidparticlesaredirectedtopassbytheporestructuresinphysicallyacceptable

paths [55].

Other relevant conditions

Thesimulateddomainisa2-Dsquareofdimensions10mm×10mmwithperiodic

boundary conditions appliedin boththe streamwiseand transverseﬂowdirections.