Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.


Sunden CH010.tex 10/9/2010 15: 22 Page 396
396 Computational Fluid Dynamics and Heat Transfer
where,u andv denotethevelocitycomponents inthestreamwise(x)andtransverse
(y) direction, respectively. In the present study, u is the total velocity in the x
direction: u=¯u+u
, and v is the velocityfluctuation in the y direction, i.e., v =v
.
ρ, and µ stand for the density and dynamic viscosity, respectively. D/Dt is the
material derivative. F
B
(N/m
3
) is the applied body force, which is used to balance
the electromagnetic force in the x direction, and is given by:
F
B
= σ(B sinθ)
2
U
0
(34)
10.3.3 SPH analysis of magnetic conditions to restrain the transition
to turbulence
SPH simulations are performed with respect to the channel flow configuration
shown in Figure 10.6. The separation distance between the two parallel infinite
plates (L) is takenas 1.0m.The computational domain isaunit square where solid
boundaries confine the flow in the transverse direction (y) and periodic boundaries
arespecifiedintheflowdirection(x).Thesimulationisstartedwiththefluidmoving
tothe right(positivex)at avelocity, U
0
=1.0m/s.TheReynolds numberis defined
as Re=UL/ν, with U, L being the characteristic velocity (1.0m/s) and length
(1.0m), respectively, and the kinematic viscosity, ν, is adjusted to give different
Reynolds numbers. The initial arrangement of the SPH particles and treatment of
solid wall boundaries were already illustrated inFigure 10.1.A 50square lattice of
fluid particles is used.
Theintensityoftheelectromagneticforcecanbequantifiedwithadimensionless
quantity, namely, Stuart number St, which is defined as:
St = Re
m
Al =
σB
2
L
m
ρU
m
(35)
where, Al denotes the Alfvén number. The Stuart number St designates the ratio
of the electromagnetic force to the inertial force. It is assumed that the magnetic
characteristic velocity U
m
and lengthL
m
have thesame magnitudes of theirhydro-
dynamic counterparts, i.e., 1.0m/s for U
m
and 1.0m for L
m
.The magnitude of the
applied magnetic field B is adjusted to give different values of St.
Transitional organization of the SPH fluid particles versus the onset
of turbulence
For SPH simulations, the onset of turbulence is accompanied by an ordered–
disordered transition of the SPH fluid particles [14, 24], so the transitional
organization of the SPH fluid particles indicates the time when the onset of tur-
bulence takes place. ForfluidflowofRe=10
4
and St=40 with the magnetic field
alignedalongthe streamwiseflowdirection, i.e.,θ =0
◦
, atthetimeof1.89 seconds
the SPH particles display an ordered flow pattern, which takes on a plug flow pro-
file withvery thinboundary layers.At 1.95secondsthe transitionalorganizationof
SPH fluid particles begins to appear, which indicates that the flow turbulence sets

Sunden CH010.tex 10/9/2010 15: 22 Page 397
SPH – a versatile multiphysics modeling tool 397
−0.5
0.0
0.6 0.8 1.0
y/L
0.5
u (m/s)
−0.5
0.0
0.02 0.03 0.04 0.05
y/L
0.5
u ′u ′ (m
2
/s
2
)
y/L
−0.5
0.0
0.0
5.0×10
−4
1.0×10
−3
1.5×10
−3
2.0×10
−3
0.5
ν′ν′ (m
2
/s
2
)
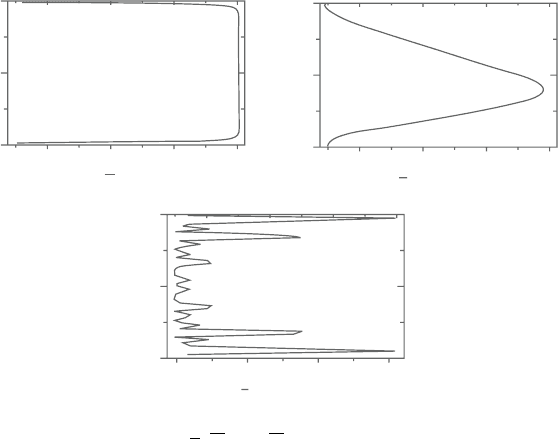
Figure 10.7. Representationof ¯u, u
¯
u
,andv
¯
v
forMHDchannelflowofRe=10
4
,
St=40, and θ =0
◦
at time ∼1.9 seconds.
in.Thecalculation isterminatedatthis pointbecause theensuing MHD turbulence
is of no immediate interest to the present study.
Further insightinto theflow statecanbe achievedbyexaminingthe turbulence-
related quantities, the mean velocity ¯u and the velocity correlations u
¯
u
and v
¯
v
.
This is done by dividing the flow domain into 50 horizontal strips and by using
a smaller time step to redo the calculations around a specified instant of time,
afterwards the results are averaged both spatially and temporally over each sub-
region. Shortly before the onset of turbulence is detected, at time ∼1.9 seconds,
theturbulence-related quantitiesof theabove-described MHDfluid floware shown
in Figure 10.7. The flow takes on some turbulent flow characteristics, namely, the
mean velocity profile is approaching to that of plug flow with the occurrence of
very thin boundary layers.
Enhanced effect of the tilting angle θ
TheMHDflowtobeconsideredinthissectionhasRe=10
4
andSt=40.Thetilting
angle θ of the applied magnetic field B to the main fluid flow direction is varied to
examinetheacquiredrestrainingeffecttothetransitiontoturbulence.Whenθ =0
◦
,
i.e., a streamwise magnetic field is applied, the flow turbulence takes place at time
∼1.95 seconds. The turbulence-related quantities at time ∼1.9 seconds, as shown
inFigure10.7, revealthe velocity correlations inthey directiontakesmaller values
thanthoseinthex direction:thevaluesofu
¯
u
areintherangeof0.015to0.06m
2
/s
2
Sunden CH010.tex 10/9/2010 15: 22 Page 398
398 Computational Fluid Dynamics and Heat Transfer
0.0
5.0×10
−15
1.0×10
−14
1.5×10
−14
y/L
−0.5
0.0
0.5
u′u ′ (m
2
/s
2
)
y/L
−0.5
0.0
0.5
0.0
6.0×10
−9
1.2×10
−8
1.8×10
−8
ν′ν′ (m
2
/s
2
)
0.94 0.96 0.98 1.00
y/L
−0.5
0.0
0.5
u (m/s)
Figure 10.8. Representation of u, u
, and v
v
for MHD channel flow of Re=10
4
,
St=40, and θ =20
◦
at time ∼5.24 seconds.
whilev
¯
v
arewithin0to0.002m
2
/s
2
,whichimpliesthatthevelocityfluctuationsin
the transverse plane of the flow are restrained by the applied streamwise magnetic
field. The largest velocity fluctuation in the y direction is detected to occur in the
region close to the walls, whereas that in the x direction takes place in the central
region of the fluid flow. This indicates the velocity fluctuation in the x direction
is initiated from the large bulk flow velocity, while the one in the y direction is
caused by the interactions between the fluid flow and the boundary walls. It is the
largevelocityfluctuationsfreelydevelopinginthex directionthatcausethevelocity
fluctuationintheydirectionandyieldthetransitionalorganizationofSPHparticles.
AneffectiveMHD methodtorestrain thetransitionto turbulenceisenhancedwhen
the applied magnetic field is capable of controlling the flow concurrently in the x
and y direction.
Atanangle ofθ =20
◦
, plugflowwith very thinboundarylayers developsgrad-
ually; although the displacement in the streamwise direction between particles in
the boundary layers and those in the main flow is cumulative with time, the flow
is laminated and the SPH particles remain ordered till the end of the simulation
(t =6.79 seconds).The corresponding turbulence-related quantities for this condi-
tion at time ∼5.24 seconds are displayed in Figure 10.8.The representation of the
meanvelocityprofiletakesona nearlyperfectplug flow:evenforthefluidparticles
close to the wall boundaries, their velocities approach the bulk velocity, 1.0m/s.
Compared to those shown in Figure 10.7, both the velocity fluctuations in the x
and y direction are restrained, even when the time is extended by approximately
3.3 seconds beyond that presented in Figure 10.7; for these conditions the

Sunden CH010.tex 10/9/2010 15: 22 Page 399
SPH – a versatile multiphysics modeling tool 399
fluctuationsare atamuch lower level,namely: u
¯
u
iswithin 0to1.5×10
−14
m
2
/s
2
and v
¯
v
within 0 to 2.0×10
−8
m
2
s
2
. The velocity fluctuation in either the x or
y direction gets effectively damped, and although the electromagnetic force pre-
scribed in the y direction diminishes, the restraining effect exerted on the velocity
fluctuations in this direction seems to become stronger, not weaker. This is seem-
ingly unreasonable; however, it may be explained on the basis of what is observed
inFigure10.7: the velocity fluctuationsin thex directionare notconstrained by the
applied streamwise magnetic field, thus they have very large values; these velocity
fluctuations in the x direction transfer “turbulent” energy to the velocity fluctua-
tions in the y direction, which, in turn, also acquire large values.This supports the
viewpointadvanced above: an effectiveMHDmethod for restraining the transition
to turbulence needs to suppress simultaneously the velocity fluctuations in the x
and y direction.
Ten SPH simulations were performed for θ =0, 10, 20, 30, 40, 50, 60, 70, 80,
and90
◦
, respectively.All theresultsare listedinTable10.1.Anapplied streamwise
magnetic field (θ =0
◦
) is more effective in restraining the velocity fluctuations in
they direction,but ithasno influenceonthevelocityfluctuationsinthex direction.
Table 10.1. Restrainingeffectuponthetransitiontoturbulence bythetiltingangle
θ (Re=10
4
,St=40)
θ(
◦
) Onset of turbulence Turbulence-related quantities
at time equal
¯u
b
u
¯
u
v
¯
v
to (seconds)
c
90 0.96 0.991 0–4.3×10
−11
0–0.068
c
80 1.02 0.99 0–1.1×10
−11
0–0.014
c
70 1.23 0.989 0–4.2×10
−12
0–0.011
c
60 1.85 0.988 0–1.1×10
−12
0–0.006
a
50 – 0.985 0–5.4×10
−17
0–9.2×10
−9
a
40 – 0.978 0–5.1×10
−18
0–1.2×10
−8
a
30 – 0.965 0–5.7×10
−18
0–2.2×10
−8
a
20 – 0.93 0–1.5×10
−14
0–2.0×10
−8
a
10 – 0.78 0–8.0×10
−7
0–3.5×10
−8
c
0 1.95 0.55 0.015–0.06 0–2.1×10
−3
a
Up to the end of simulation time, 6.79 seconds, turbulence is practically not detected.
The turbulence-related quantities are calculated at time ∼5.24 seconds.
b
In the central region of the fluid flow, the average velocity is about 1.0m/s. The datum
shown here is the velocity of the fluid particle closest to the wall.
c
The turbulence-related quantities are calculated shortly before the onset of turbulence.
For instance, the turbulence quantities shown in the last row are calculated around at
1.90 seconds.
Sunden CH010.tex 10/9/2010 15: 22 Page 400
400 Computational Fluid Dynamics and Heat Transfer
It is the fast growth of the velocity fluctuations in the x direction that leads to the
early turbulence onset (1.95 seconds).With increasing θ (θ =10 to 50
◦
), the mean
flowvelocityprofileapproachestheplugflowmoreclosely;thevelocityfluctuations
in the x direction are effectively restrained due to the increasing electromagnetic
force produced in this direction; although the y-component of the electromagnetic
force decreases, the restraining effect exerted on the velocity fluctuations in the y
directionbenefits fromthe effective constraintof itscounterpartsinthex direction.
Further increase of θ (θ =60 to 80
◦
) yields the renewed appearance of turbulence,
largely dueto theincrease ofthe velocityfluctuations inthe y direction.An applied
transverse magnetic field (θ =90
◦
) is more effective in controlling the mean flow
profile, but it does not restrain well the transition to turbulence.Turbulence occurs
at an earlier time (0.96 seconds), when the applied magnetic field is aligned with
the transverse direction.
Enhanced conditioning effect of the transition to turbulence is obtained when
the oblique angle θ is within the range 20 to 50
◦
. In this situation, the mean flow
velocityprofileis closetoaperfectplug flow;thevelocityfluctuationsin boththex
and y directionare keptatvery low levels, namely: u
¯
u
is below1.5×10
−14
m
2
/s
2
and v
¯
v
less than 2.2×10
−8
m
2
/s
2
; and, effectively, the onset of flow turbulence
does not take place up to the end of the simulation time (6.79 seconds).
SPH simulations were also conducted with a magnetic field, B, increased by a
factorof10togiveaStuartnumber,St, of4,000fortheMHDflowofRe=10
4
with
the θ varying in the range of 0 to 90
◦
. For the range 10
◦
≤θ ≤80
◦
the transition to
turbulence getseffectively suppressed; even so, forthe magnetic supply conditions
of θ =0 and 90
◦
with this increased magnetic field applied, the flow turbulence
still appears, which supports the viewpoint advanced above; an effective MHD
method for restraining the transition to turbulence requires a strategy that restrains
all velocity fluctuation components simultaneously.
10.4 SPH Numerical Modeling for Ballistic-Diffusive
Heat Conduction
Design of nanoscale systems, such as semiconductor devices based on the GaAs
MESFETs or Si MOSFETs, and ultrafast (picoseconds or even femtoseconds)
pulsed lasers have forced a fresh look into fundamental heat transfer issues [26].
At nanoscale level, the classical Fourier heat diffusion is not valid due to: (a)
the mean free path of the energy carriers becomes comparable to or larger than
the characteristic length scale of the particular device/system, and/or (b) the time
scale of the processes becomes comparable to or smaller than the relaxation time
of the energy carriers. Numerical solutions either using the Boltzmann transport
equation (BTE) or using atomic-level simulations such as the molecular dynamics
simulation (MDS) and Monte Carlo simulation (MCS) are helpful in understand-
ing the physics of heat transfer in this regime; however, these options require
large computational resources, which make them not ver y effective analytical
tools for the design/management of devices in practical nanoscale engineering.

Sunden CH010.tex 10/9/2010 15: 22 Page 401
SPH – a versatile multiphysics modeling tool 401
The Cattaneo-Vernotte (C-V) hyperbolic equation [27], for a while, seemed to be
a convenient alternative approach, since it excludes the so-called infinite thermal
propagation speed assumption implied in Fourier law. The work reported by Haji-
Sheikh et al. [28] was the first one to point out certain anomalies existing in the
hyperbolic solutions. Further on, recentworkby JiangandSousa [29] also demon-
strated the presence of hyperbolic anomalies in a hollow sphere with the Dirichlet
boundary conditionprescribed.Although mayexistsomeremedies [28]totheC–V
equation, a newly developed heat conduction formulation, known as the ballistic-
diffusive equation [30, 31], seems to be a viable candidate for applications in this
particular field.
The key concept of the model, on which the ballistic-diffusive heat conduc-
tion equation is formulated, is to split the heat carriers inside the medium into two
components – ballistic and diffusive. The ballistic component is determined from
the prescribedboundary conditionand/or nanoscale heatsources, and it only expe-
riences outscattering; the transport of the scattered and excited heat carriers inside
the medium is treated as a diffusive component. This approach has its origin in
methodologies used to deal with radiative heat transfer [32, 33].
The ballistic-diffusive equation is derived on the basis of the BTE under the
relaxation time approximation; it differs, in appearance, from the C–V equation
mainly by having the additional ballistic term, namely
τ
∂
2
u
m
∂t
2
+
∂u
m
∂t
=∇
λ
C
∇u
m
−∇·q
b
+
S + τ
∂S
∂t
(36)
where, C refers to the volumetric specific heat (J/m
3
K), q
b
to the ballistic heat
flux vector (W/m
2
), S to the heat generation (W/m
3
), t to time (seconds), u
m
to the
internal energy per unit volume (J/m
3
), λ to the heat conductivity (W/m K), and τ
to the thermal relaxation time (seconds).The heat generation S is assumed to have
a much larger feature size than the mean free path of the heat carriers; otherwise it
should be treated as a ballistic term also. In the original work of Chen [30, 31], the
following general boundary condition for the diffusive components is as follows:
τ
∂u
m
∂t
+ u
m
=
2
3
∇u
m
· n (37)
where,n (boldtextdesignates vector)is theinwardunitvector perpendicular tothe
boundary, and is the meanfree path of heatcarrier (m).The ballisticheat flux q
b
is given by an algebraic analytical expression [31, 34]; however, the full solution
of equation (36) still has to resort to an appropriate numerical method, in general,
the finite difference or finite element method.
Thepresent sectionaims toshow theviability andaccuracyof theSPH solution
oftheone-dimensional(1-D)modelproposedbyChen[31].Itshouldbementioned
thatSPHwasalreadyemployedtosolvetheFourier heatconductionequationswith
satisfying results [3, 4, 35], and acorrectiveSPH method [35] is used by Chen and
Beraun[36] tosolve thenon-classicheattransferprocessinthin metalfilms heated
by ultrashort laser pulse [37].

Sunden CH010.tex 10/9/2010 15: 22 Page 402
402 Computational Fluid Dynamics and Heat Transfer
10.4.1 Transient heat conduction across thin films
In Chen [31] it is reported that the application of the ballistic-diffusive model to a
transientheatconductionprocessinthinfilms.Thesamethermalcaseisconsidered
in the present study: a thin (nanoscale) film of thickness L with constant thermal
properties initially at ambient temperature T
0
; at the time t ≥0, one boundary
surface emits phonons at temperature T
1
; both boundary surfaces are black body
emittersandthere isnoheatgeneration insidethefilm.Thedimensionlessballistic-
diffusive equation and associated initial and boundary restrictions can be written
as in Chen [31].
∂
2
θ
m
∂t
∗2
+
∂θ
m
∂t
∗
=
Kn
2
3
∂
2
θ
m
∂η
2
− Kn
∂q
∗
b
∂η
(38)
t
∗
= 0, θ(η,0)= 0
∂θ(η,t
∗
)
∂t
∗
t
∗
=0
= 0 (39)
η = 0,
∂θ
m
∂t
∗
+ θ
m
η=0
=
2Kn
3
∂θ
m
∂η
η=0
(40)
η = 0, θ
b1
= 1 (41)
η = 1,
∂θ
m
∂t
∗
+ θ
m
η=1
=−
2Kn
3
∂θ
m
∂η
η=1
(42)
η = 1, θ
b2
= 0 (43)
where, η and θ
m
are the dimensionless coordinate and diffusive temperature,
respectively.
The boundary heat flux, its derivative, and thetemperature of the ballistic com-
ponents have their algebraic analytical expressions [31] given in non-dimensional
form as:
q
∗
b
(η,t
∗
) =
⎧
⎪
⎨
⎪
⎩
1
2
&
1
µ
t
µe
−(η/µKn)
dµ
0 ≤ µ
t
=
x
vt
≤ 1
0 other µ
t
(44)
∂q
∗
b
η,t
∗
∂η
=
⎧
⎪
⎨
⎪
⎩
−
1
2Kn
&
1
µ
t
e
−
(
η/µKn
)
dµ +
η
Knt
∗2
e
−t
∗
(
0 ≤ µ
t
≤ 1
)
0 other µ
t
(45)
θ
∗
b
η,t
∗
=
⎧
⎪
⎨
⎪
⎩
1
2
&
1
µ
t
e
−
(
η/µKn
)
dµ
(
0 ≤ µ
t
≤ 1
)
0 other µ
t
(46)

Sunden CH010.tex 10/9/2010 15: 22 Page 403
SPH – a versatile multiphysics modeling tool 403
where, µ
t
=x/(vt), v refers to the carrier group velocity (m/s), x to the coordinate
(m), and µ to the directional cosine.
The non-dimensional parameters are defined as follows:
θ
m
=
u
m
− u
m0
CT
,θ
b
=
u
b
− u
b0
CT
,q
∗
m
=
q
m
− q
m0
CvT
,q
∗
b
=
q
b
− q
b0
CvT
,
(47)
t
∗
= t/τ,η = x/L
with
Kn = /L, T = T
1
− T
0
(48)
where,KnreferstothephononKnudsennumber,Ltothethicknessofthenanoscale
thin film (m), T
0
and T
1
are the initial temperature (K) and the phonon emission
temperature at the left boundary (K), respectively.
Thus, the total temperature and heat flux are defined by:
θ =
u −u
0
CT
=
T − T
0
T
, q
∗
=
q −q
0
CvT
(49)
The diffusive component of the heat flux is governed by the following equation.
∂q
∗
m
∂t
∗
+ q
∗
m
=−
Kn
3
∇θ
m
(50)
where, q
∗
m
is the dimensionless diffusive heat flux.
In Chen [31] the above set of equations were solved numerically with the finite
difference method (FDM) and the results were compared against those obtained
using: (a) the direct solution of the BTE, (b) the Cattaneo hyperbolic heat conduc-
tion equation [27], and (c) the classic Fourier heat diffusion equation. Relative to
the BTE results, the ballistic-diffusion heat conduction equation gives consistent
temperature and heat flux profiles, whereas the Cattaneo and Fourier heat conduc-
tion model both lead to erroneous representations of the processes. In the present
study, the ballistic-diffusive equation is to be solved with the SPH method.
10.4.2 SPH modeling
Intheimplementation ofthe SPHmethod tosolvetheheat conduction,the thermal
action attime t is represented by a collectionof N particles located ata position r
i
,
i =1,2, ……,N.The“smoothed”valueofanyfieldquantityf (r, t)ata spacepoint
r and at a time t is a weighted sum of all contributions from neighboring particles
f (r,t)=
N
j=1
V
j
f (r
j
,t)w
|r −r
j
|,h
(51)
where, N refers to the total SPH particle number.

Sunden CH010.tex 10/9/2010 15: 22 Page 404
404 Computational Fluid Dynamics and Heat Transfer
Sincetheparticledensityremainsconstanthere,theweightisthevolumeofSPH
particle instead of the quotient of mass and density [9]. The first order derivative
of f (r, t) is written as:
∇f (r,t)=
N
j=1
V
j
f (r
j
,t)∇w(|r − r
j
|,h) (52)
Equation (52) is not symmetric; however, by using the following mathematical
operator
∇f =
∇
(
χ f
)
− f ∇χ
χ
(53)
where, χ is unity, equation (52) can be rewritten in the following symmetric form:
∇f (r,t)=
N
j=1
V
j
[f
(
r,t
)
− f (r
j
,t)]∇w(|r − r
j
|,h) (54)
In terms of equation(54), the “smoothing” formulation of thefirst-order derivative
of the temperature (θ
m
) is:
∇θ
m
(η
i
,t
∗
) =
j
V
j
[θ
m
(η
i
,t
∗
) −θ
m
(η
j
,t
∗
)]∇
i
w
ij
(55)
where, ∇
i
denotes the gradient taken with respect to the coordinates at particle i
∇
i
w
ij
=
η
ij
|η
ij
|
∂w
ij
∂η
i
(56)
and η
ij
=η
i
−η
j
and w
ij
=w(|η
i
−η
j
|,h).
One of the key issues for the SPH modeling of the ballistic-diffusive heat con-
ductionishowtoconstructthe“smoothing”formulationforthesecondderivativeof
thediffusivetemperature(θ
m
)in equation(36).A formulation, which combinesthe
standardfirst-orderSPHderivative(equation(55))andthefinitedifferenceconcept,
was first used by Brookshaw [38] and later on by Cleary and Monaghan [3]. This
procedure is computationally efficient, since it only involves the first-order deriva-
tive ofthe smoothingkernel.Althoughit doesnot conservethe angularmomentum
accurately, its use in simulations of Fourier heat conduction problems [3] has been
very successful. Itis employed in thepresent studyand has thefollowing evolution
form:
∂
2
θ
m
(η
i
,t
∗
)
∂η
2
=
j
2V
j
[θ
m
(η
i
,t
∗
) −θ
m
(η
j
,t
∗
)]
1
|η
ij
|
∂w
ij
∂η
i
(57)
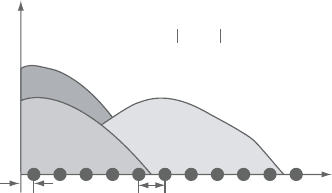
Five hundred SPH particles are uniformly distributed along the heat transfer
path. The separation distance between neighboring particles is p (=L/500).The
Sunden CH010.tex 10/9/2010 15: 22 Page 405
SPH – a versatile multiphysics modeling tool 405
W
0
∆p/2 ∆p
η
A
1
A
1
= 1, A
2
< 1, A
2
+ A
3
= 1
A = ∫ w( η − η′ , h)dη′
A
2
A
3
Figure 10.9. Illustration of SPH “near-boundary deficiency” and the boundary
treatment devised.
inner-node approach is used, which means that either the first or the last SPH
particle is not set on the boundary surfaces, but has half p distance away from
the respective adjoining boundary. The time derivatives are approximated by the
explicit central (for the second-order derivative) or by the forward (for the first-
orderderivative) scheme.The timestepisadjusted tosatisfythe numericalstability
requirements.
In this implementation, the high order 3-splines quintic kernel is also used.
10.4.3 Boundary treatment
In the present ballistic-diffusive heat conduction case, the temperature specified
at the boundary does not represent the equivalent equilibrium temperature of the
boundary; the boundary temperature and the boundary flux are calculated from
the summationof thecorresponding ballisticand diffusivecomponents.Therefore,
the temperature values of all the SPH particles depend on the smoothing interpo-
lation.This is the reason why the boundary condition requires special treatment.
On the basis of the properties of the smoothing kernel, a simple boundary
treatment is devised, as illustrated in Figure 10.9.
Oneofthe properties theSPH smoothingkernel musthave isthenormalization
property [15], that is
&
w(|η −η
|,h)dη
= 1.0 (58)
Clearly, fortheparticlesclose totheboundarythe normalizationpropertyis not
satisfied,whichisthereasonfortheSPH“near-boundarydeficiency”.Anexpedient
boundary treatmentcanbedevisedbyvarying thenormalizationconstantn
d
values
to meet the requirements set by equation (58) for all the particles. A general form
for the SPH smoothing kernel is:
w(s,h) = n
d
F(s,h) (59)
where, s=|η
ij
|/h, and F is a fitting function.
