Allman E.S., Rhodes J.A. Mathematical Models in Biology: An Introduction

Подождите немного. Документ загружается.

176 Constructing Phylogenetic Trees

.32

.18

.24

.02

.32

.18

.24

.02

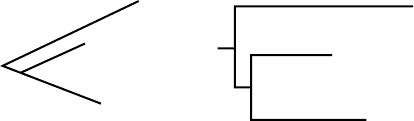
Figure 5.4. Alternate depictions of the same metric tree.

between splittings of the lineage. The longer an edge is, the more the DNA

sequence mutated in the course of the evolution that edge represents.

If, for instance, the Jukes-Cantor model of base substitution adequately

described the evolution of several taxa, then the edge length in a tree relating

them might be the Jukes-Cantor distance between the sequences at the two

ends of the edge. As we saw in Chapter 4, this distance is the average number of

base substitutions per site that occurred in the descent. Included in this are the

mutations obscured by other mutations that the distance formula was designed

to estimate. Because the Jukes-Cantor distance is additive and symmetric,

the total distance between two taxa along a tree should be the Jukes-Cantor

distance between them.

If the molecular clock assumption holds for the evolution of the sequences

being related, then the distances in a tree have a more direct meaning. Recall

that a molecular clock just means that the mutation rate is constant for all

lineages under consideration. If µ denotes the mutation rate, measured in

(base substitutions per site)/year, for instance, and t denotes a time in years,

then the amount of mutation that will occur during this time is

d = µt base substitutions per site.

Thus, a molecular clock means that the amount of mutation along any edge is

proportional to the elapsed time, with the constant of proportionality being the

constant rate of mutation. Under the assumption of a molecular clock, then,

whether we draw edge lengths representing amount of mutation or elapsed

time, we draw exactly the same ﬁgure, up to scaling by this constant.

If the molecular clock hypothesis holds for a rooted metric tree, then every

leaf will be located the same total distance from the root. This is because

distances from the root are proportional to the elapsed time since the taxa

began to diverge from the common ancestor. Every taxon has had the same

amount of time to evolve from the root ancestor, so each will have accumulated

the same amount of mutation.

5.1. Phylogenetic Trees 177

Without a molecular clock, the relationship between the amount of mu-

tation along an edge and the amount of time may be complicated. Suppose

that, along one edge of a phylogenetic tree, the mutation rate was quite small,

and along another, the mutation rate was large. Then, even though both edges

might correspond to the same amount of time, considerably more mutation

would occur along one. Without somehow getting additional information

about the rate of mutation – perhaps by comparisons to the fossil record –

we usually do not have ways of determining elapsed times associated to tree

edges.

Metric trees are sometimes drawn in a “square” manner so that it is easier

to compare distance along various evolutionary paths. As an example, the two

trees in Figure 5.4 both represent the same information. In the tree on the left,

the edges have speciﬁed lengths, and in the tree on the right, the horizontal

edges have those same lengths. Thus, the vertical edges on the right-hand tree

are read as contributing nothing to the amount of mutation; they serve solely

to separate the various lineages for increased readability.

Problems

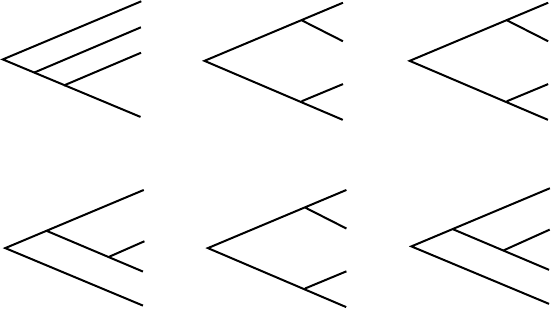
5.1.1. Consider the trees in Figure 5.5.

a. Which of them are the same, as rooted metric trees?

b. Which of them are the same, as unrooted metric trees?

Figure 5.5. Trees for Problem 5.1.1.

178 Constructing Phylogenetic Trees

c. Which of them are the same, as rooted topological trees?

d. Which of them are the same, as unrooted topological trees?

e. For which trees does a molecular clock appear to be operating?

5.1.2. a. Draw the single topologically distinct unrooted bifurcating tree that

could describe the relationship between 3 taxa.

b. Draw the three topologically distinct rooted bifurcating trees that

could describe the relationship between 3 taxa.

5.1.3. a. Draw all 3 topologically distinct unrooted bifurcating trees that

could describe the relationship between 4 taxa.

b. Draw all 15 topologically distinct rooted bifurcating trees that could

describe the relationship between 4 taxa.

5.1.4. For n terminal taxa, the number of unrooted bifurcating trees is

1 · 3 · 5 ···(2n − 5) =

(2n − 5)!

n−3

(n − 3)!

Make a table of values and graph this function for n ≤ 10.

5.1.5. For n terminal taxa, the number of rooted bifurcating trees is

1 · 3 · 5 ···(2n − 3) =

(2n − 3)!

n−2

(n − 2)!

Make a table of values and graph this function for n ≤ 10.

5.1.6. In this problem, we will step through the reasoning behind the formulas

for the number of topologically distinct trees, rooted and unrooted.

a. Suppose we already know that an unrooted tree with n terminal

vertices is made up of e edges. Explain why an unrooted tree with

n + 1 terminal vertices will have e + 2 edges. (Hint: Think about

how adding one more terminal vertex to an existing tree affects the

number of edges.)

b. Because an unrooted tree with 2 terminal vertices has 1 edge, explain

from part (a) why an unrooted tree with n terminal vertices will have

1 + 2(n − 2) = 2n − 3 edges.

c. Suppose we know there are m unrooted trees with n terminal ver-

tices. Explain why there will be (2n − 3)m unrooted trees with n + 1

terminal vertices. (Hint: Think about how many different ways you

can add one more terminal vertex to an existing tree.)

d. Because there is only 1 unrooted tree with 2 terminal vertices, ex-

plain from part (c) why there are 1 · 3 · 5 ···(2n − 5) unrooted trees

with n terminal vertices when n > 2.

5.1. Phylogenetic Trees 179

e. Explain why

1 · 3 · 5 ···(2n − 5) =

(2n − 5)!

n−3

(n − 3)!

f. Why is the number of rooted trees with n terminal vertices the same

as the number of unrooted trees with n + 1 terminal vertices?

g. Conclude that the formulas of Problems 5.1.4 and 5.1.5 are correct.

5.1.7. Because mitochondrial DNA in humans is inherited solely from the

mother, it can be used to construct a tree relating any number of humans

from different ethnic groups, assuming we all descended from a single

ﬁrst human female. Depending on the clustering pattern of the ethnic

groups, this might give insight into the physical location of this woman

sometimes called Mitochondrial Eve.

In (Cann et al., 1987), a work that ﬁrst purported to locate Mito-

chondrial Eve in Africa, supporting the “out of Africa” theory of human

origins, a rooted tree was constructed that was claimed to show the rela-

tionships between 147 individuals. How many topologically different

trees would need to be looked at if every possibility was really exam-

ined? (You may need to use Stirling’s formula: n! ∼

√

2πn

−n

Here, the symbol “∼” can be interpreted as “is approximately.”)

See (Gibbons, 1992) for the fall-out from the difﬁculty of consid-

ering so many trees.

5.1.8. The phylogeny of four terminal taxa A, B, C, and D are related ac-

cording to a certain metric tree. The total distances between taxa along

the tree have been found to be as in Table 5.1.

a. Using any approach you wish, determine the correct unrooted tree

relating the taxa, as well as all edge lengths. Explain how you rule

out other topological trees.

b. Can you determine the root from this data? Explain why or why not.

Note: Techniques for this sort of problem are the subject of the next

few sections.

Table 5.1. Distances Between Taxa for

Problem 5.1.8

ABCD

A .6.6.2

B.4.6

C.6

180 Constructing Phylogenetic Trees

5.2. Tree Construction: Distance Methods – Basics

In constructing a phylogenetic tree, the taxa we wish to relate are usually

ones currently living. We have information, such as DNA sequences, from

the terminal taxa and no information from the ones represented by internal

vertices. Indeed, we do not even know which internal vertices should exist,

because we do not yet know the tree topology.

The ﬁrst class of methods for constructing phylogenetic trees that we will

discuss are distance methods. These attempt to build a tree using information

that we believe describes the total distances between terminal taxa along the

tree.

To see how we might obtain these distances, imagine trying to ﬁnd the

evolutionary relationship of four species: S1, S2, S3, and S4. Choosing a

particular orthologous stretch of DNA from their genomes, we obtain and

align sequences from each. If the Jukes-Cantor model of base substitution

discussed in Chapter 4 seems appropriate for the data, we then compute Jukes-

Cantor distances between each pair of sequences. These are our estimates of

distances along the tree, which we organize in Table 5.2.

Table 5.2. Distances Between Taxa

S1 S2 S3 S4

S1 .45 .27 .53

S2 .40 .50

S3 .62

Depending on the sequence data, we might instead adopt a different model

of base substitution, leading us to use a different distance formula, such as

the Kimura 2-parameter or the log-det distance. Regardless, the distance we

calculate between sequences is believed to be a measure of the amount of

mutation that has occurred. If these distances were an exact measure of the

amount of mutation that occurred, they would match up with the total distances

between terminal taxa in the metric tree we would to ﬁnd.

We do not really expect to ﬁnd a tree that this data ﬁts exactly; after all, the

distances are inferred from sequence data and are not expected to be exactly

correct. Moreover, the method of inferring the distances depended on a model

that involved assumptions that are certainly not met in real organisms. We

hope that however we construct a tree will not be too sensitive to these sorts

of errors in the distances.

UPGMA. The ﬁrst method we consider is called the average distance

method, or, more formally, the unweighted pair-group method with arithmetic

5.2. Tree Construction: Distance Methods – Basics 181

means (UPGMA). This method produces a rooted tree and assumes a mole-

cular clock. The easiest way to understand the algorithm is by following an

example of its use.

With the data table above, we pick the two closest taxa, S1 and S3. Because

they are .27 apart, we draw Figure 5.6 with each edge .27/2 = .135 long.

.135

Figure 5.6. UPGMA; step 1.

We then combine S1 and S3 into a group, and average the distances of S1

and S3 to each different taxon to get the distance from the group to that taxon.

For example, the distance between S1–S3 and S2 is (.45 + .40)/2 = .425,

and the distance between S1–S3 and S4 is (.53 + .62)/2 = .575. Our table

thus collapses to Table 5.3.

Table 5.3. Distances Between

Groups; UPGMA, Step 1

S1–S3 S2 S4

S1–S3 .425 .575

S2 .50

Now, we simply repeat the process, using the distances in the collapsed

table. Because the closest taxa and/or groups in the new table are S1–S3 and

S2, which are .425 apart, we draw Figure 5.7.

.135

.0775

.2125

Figure 5.7. UPGMA; step 2.

182 Constructing Phylogenetic Trees

The edge to S2 must have length .425/2 = .2125, while the other new

edge must have length (.425/2) − .135 = .0775, because we already have

the edges of length .135 to account for some of the distance between S2 and

the other taxa.

Again combining taxa, we form a group S1–S2–S3, and compute its dis-

tance from S4 by averaging the original distances from S4 to each of S1,

S2, and S3. This gives us (.53 + .5 + .62)/3 = .55. (Note that this is not the

same as averaging the distance from S4 to S1–S3 and to S2.) Because a new

collapsed distance table would have this as its only entry, there is no need to

give it. We draw Figure 5.8, estimating that S4 is .55/2 = .275 from the root.

The ﬁnal edge has length .0625, since that places the other taxa .275 from the

root as well.

.135

.0775

.0625

.275

.2125

Figure 5.8. UPGMA; step 3.

As we suspected, the tree we have constructed for the data does not exactly

ﬁt the data. The distance on the tree from S3 to S4, for instance, is .55, although

according to the original data, it should be .62. Nonetheless, the tree distances

are at least reasonably close to the distances given by the data.

If we had more taxa to relate, we would have to do more steps to complete

the UPGMA process, but there would be no new ideas involved. At each step,

we join the two closest taxa or groups together, always placing them at equal

distances from a common ancestor. We then collapse the joined taxa into a

group, using averaging to compute a distance from that group to the taxa and

groups still to be joined. The one point to be particularly careful about is

that when the distances between two groups are computed, we must average

all the distances from members of one group to another – if one group has

n members and another has m members, we have to average nm distances.

Each step of the algorithm reduces the size of the distance table by one, so

that after enough steps, all of the taxa are joined into a single tree.

5.2. Tree Construction: Distance Methods – Basics 183

Notice that the molecular clock assumption is implicit in UPGMA. In this

example, when we placed S1 and S3 at the ends of equal length branches, we

assumed that the amount of mutation each underwent from their common an-

cestor was equal. UPGMA always places all the taxa at the same distance from

the root, so that the amount of mutation from the root to any taxon is identical.

Fitch-Margoliash algorithm. This method is a bit more complicated than

UPGMA, but builds on its basic approach. However, it attempts to drop the

molecular clock assumption of UPGMA.

Before giving the algorithm, we need a few mathematical observations.

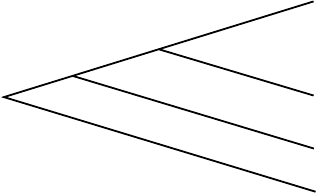
First, if we attempt to put 3 taxa on an unrooted tree, then there is only one

topology that needs to be considered. Furthermore, for 3 taxa, we can assign

lengths to the edges to ﬁt the data exactly. To see this, consider the tree in

Figure 5.9. If we have some distance data d

, d

, and d

, then

x + y = d

x + z = d

y + z = d

These equations can be solved either by writing the system as a matrix equa-

tion and ﬁnding an inverse, or by substituting formulas for one variable ob-

tained from one of the equations into the others. Either way leads to the

solution

x = (d

+ d

− d

)/2,

y = (d

+ d

− d

)/2,

z = (d

+ d

− d

)/2.

(5.1)

We will refer to these formulas as the 3-point formulas for ﬁtting taxa to

a tree. Unfortunately, with more than 3 taxa, exactly ﬁtting data to a tree is

usually not possible. The Fitch-Margoliash (cited in tables as FM) algorithm

uses the 3 taxa case, however, to handle more taxa.

Now we explain the operation of the algorithm with an example. We’ll use

the distance data in Table 5.4.

Figure 5.9. The unrooted 3-taxon tree.

184 Constructing Phylogenetic Trees

Table 5.4. Distances Between Taxa

S1 S2 S3 S4 S5

S1 .31 1.01 .75 1.03

S2 1.00 .69 .90

S3 .61 .42

S4 .37

We begin by choosing the closest pair of taxa to join, just as we did with

UPGMA. Looking at our distance table, S1 and S2 are the ﬁrst pair to join. In

order to join them without placing them at an equal distance from a common

ancestor, we temporarily reduce to the 3-taxa case by combining all other

taxa into a group. For our data, we thus introduce the group S3–S4–S5. We

ﬁnd the distance from each of S1 and S2 to the group by averaging their

distances to each group member. The distance from S1 to S3–S4–S5 is thus

d(S1, S3–S4–S5) = (1.01 + .75 + 1.03)/3 = .93, whereas the distance from

S2 to S3–S4–S5 is d(S2, S3–S4–S5) = (1.00 + .69 + .90)/3 = .863. This

gives us Table 5.5.

Table 5.5. Distances Between

Groups; FM Algorithm, Step 1a

S1 S2 S3–S4–S5

S1 .31 .93

S2 .863

With only three taxa in this table, we can exactly ﬁt the data to the tree

using the 3-point formulas to get Figure 5.10. The key point here is that the

3-point formulas, unlike UPGMA, can produce unequal distances of taxa

from a common ancestor.

.7415

.1885

.1215

S3-S4-S5

Figure 5.10. FM algorithm; step 1.

We now keep only the edges ending at S1 and S2 in Figure 5.10 and

return to our original data. Remember, the group S3–S4–S5 was only needed

temporarily so we could use the 3-point formulas; we did not intend to join

5.2. Tree Construction: Distance Methods – Basics 185

those taxa together yet. Because we have joined S1 and S2, however, we

combine them into a group for the rest of the algorithm, just as we would

have done with UPGMA. This gives us Table 5.6.

Table 5.6. Distances Between Groups; FM

Algorithm, Step 1b

S1–S2 S3 S4 S5

S1–S2 1.005 .72 .965

S3 .61 .42

S4 .37

We again look for the closest pair (now S4 and S5) and join them in a similar

manner. We combine everything but S4 and S5 into a single temporary group

S1–S2–S3 and compute d(S4, S1–S2–S3) = (.75 + .69 + .61)/3 = .683 and

d(S5, S1–S2–S3) = (1.03 + .90 + .42)/3 = .783. This gives us Table 5.7.

Applying the 3-point formulas to Table 5.7 produces Figure 5.11.

Table 5.7. Distances Between Groups; FM

Algorithm, Step 2a

S1–S2–S3 S4 S5

S1–S2–S3 .683 .783

S4 .37

S1-S2-S3

.548

.135

.235

Figure 5.11. FM algorithm; step 2.

We keep the edges joining S4 and S5 in Figure 5.11, discarding the edge

leading to the temporary group S1–S2–S3. Thus we now have two joined

groups, S1–S2 and S4–S5. To compute a new table containing these two

groups we have found, we average d(S1–S2, S4–S5) = (.75 + 1.03 + .69 +

.90)/4 = .8425 and d(S3, S4–S5) = (.61 + .42)/2 = .515. We have already

computed d(S1–S2, S3) so we produce Table 5.8. At this point, we can ﬁt a