Акулиничев Ю.П., Дроздова В.И. Теория информации
Подождите немного. Документ загружается.

41
()
(
)()
(
)
(
)
;.
I
Xt Yt HXt H Xt Yt=−
(2.4.8)
Возможен и другой способ вычисления средней энтропии
(условной и безусловной) дискретной стационарной случайной
последовательности, приводящий к тем же результатам.
Энтропия последовательности X(t) равна
()
() () ()
11
lim , ,
nn
n
HXt HX X X
−
→∞
=
K
(2.4.9)
и характеризует среднее количество дополнительной информа-
ции, доставляемой одним символом в реализациях бесконечной
длины.
Средняя условная энтропия последовательности Х(t) вы-
числяется по формуле
()
(
)
() () () () ()
111
lim , , , , , .
nnn
n
HXtYt
HX X X Y Y
−
→∞
=
……
(2.4.10)
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 2.4.1. Сообщение X есть стационарная последова-
тельность независимых символов, имеющих ряд распределения
Сигнал Y является последователь-
ностью двоичных символов, связанных
с сообщением следующим неудачным
образом: x
1
→00, x
2
→00, x
3
→1.
Определить: а) средние безусловную и условную энтропии,
приходящиеся на 1 символ сообщения;
б) средние безусловную и условную энтропии, приходя-
щиеся на 1 символ сигнала;
в) среднюю взаимную информацию в расчете на 1 символ
сообщения.
Решение. Символы в последовательности на выходе источ-
ника независимы, поэтому из (2.4.3)
(
)
(
)
[]
1
0, 2 log 0, 2 0,1 log 0,1 0,7 log 0, 7 1,1568 áèò/ñèì â.
HXt H Xt HX===
−⋅ −⋅ −⋅ =
x
j
x
1
x
2
x
3
p(x
j
) 0,2 0,1 0,7
=
42
Обозначив y
1
=00, у
2
=1, вычислим условные и безусловные
вероятности сигнала:
(
)
(
)
(
)
()() ()
11 1 2 13
21 22 23
1, 0,
0, 1,
py x py x py x
py x py x py x
=
==
=
==
(
)
(
)
(
)
(
)
(
)
()
()
()
1111212
313
2
0, 2 0,1 0,3,
0,7.
py px py x px py x
px py x
py
=
++
=+=
=
Энтропия случайной величины Y равна
(
)
0,3 log 0,3 0,7 log 0,7 0,8813 áèòHY =− ⋅ − ⋅ = ,
а условная энтропия H(Y/X)=0, так как сигнал однозначно опре-
деляется сообщением.
Взаимная информация
(
)
(
)
(
)
; 0,8813 áèòIXY HY HYX=− = .
Условная энтропия сообщения
(
)
(
)
(
)
; 1,1568 0,8813 0,2755 áèòHXY HX IXY=− =− = .
Итак, получаем, что условная энтропия сообщения равна
0,2755 бит/симв, а взаимная информация в расчете на 1 символ
сообщения равна 0,8813 бит/симв.
Среднее количество символов сигнала, приходящихся на
1 символ сообщения, равно
()
3
1
0, 2 2 0,1 2 0,7 1 1,3 ñèì â,
jj
j
Lpxl
=
= = ⋅+ ⋅+ ⋅=
∑
где l
j
– длина кодового слова, соответствующего x
j
.
Энтропия последовательности Y(t) равна
(
)
( ) 0,8813 1,3 0,6779 áèò/ñèì â,HYt HY L== =
а условная энтропия равна нулю.
Пример 2.4.2. Вычислить энтропию однородной неразло-
жимой марковской последовательности, заданной матрицей ве-
роятностей переходов
() ( )
(
)
1kk
pX X
−
от символа
()
1k
X
−
к
символу
()
k
X
(табл. 2.4.1).
+

43
Решение. Однородность последова-
тельности проявляется в том, что при
k →∞безусловная вероятность p
j
того,
что k-й символ примет значение x
j
, не зави-
сит от k и от значения первого символа и
связана с вероятностями переходов
() ( )
()
1kk
rj j r
ppxx
−
=
уравнением
1
.
m
jrrj
r
p
pp
=
=
∑
Записываем это уравнение для каждого j и получаем систе-
му уравнений
1111221331
2 1 12 2 22 3 32
3 1 13 2 23 3 33
,
,
.
p
pp pp pp
p
pp pp pp
p
pp pp pp
=
++
=++
=++
Подставляем численные значения вероятностей переходов
и получим
123
123
123
0,8 0,3 0,6 0,
0,4 0,5 0,1 0,
0,4 0,2 0,7 0.
pp p
ppp
ppp
−
++=
−+=
+−=
Определитель этой системы равен нулю, поэтому вероятно-
сти p
j
определяется с точностью до постоянного множителя.
Выбираем его так, чтобы выполнялось условие нормировки
123
1,ppp++= и получим
p
1
= 0,3548, р
2
= 0,3441, р
3
= 0,3011.
Энтропия последовательности Н[Х(t)] по смыслу есть сред-
няя дополнительная (условная) информация, приносимая одним
символом последовательности, поэтому для марковской после-
довательности ее можно вычислить по формуле (2.4.9)
()
() ( )
()
() ( )
()
11
1
11
log 0,3548 1,5219 0,3441 1,4855
0,3011 1, 2955 1,4412 áèò ñèì â.
m
kk kk
j
j
mm
jjrjr
jr
HXt Hx X pHX X
ppp
−−
=
==
== =
==⋅+⋅+
⋅=
∑
∑∑
Таблица 2.4.1
X
(k-1)
X
(k)
x
1
x
2
x
3
x
1
0,2 0,3 0,6
x
2
0,4 0,5 0,1
x
3
0,4 0,2 0,3
+
44
3 НЕПРЕРЫВНЫЕ КАНАЛЫ
3.1 Взаимная информация
Определение непрерывного канала. Непрерывным назы-
вается канал, в котором сигналы на входе x(t) и выходе y(t) яв-
ляются реализациями непрерывных случайных функций.
В дальнейшем в качестве входного и выходного сигналов
будут рассматриваться только такие функции, спектр которых
заключен в ограниченной полосе частот от 0 до F
B
. Такие функ-
ции полностью определяются последовательностью отсчетов,
взятых с шагом 12
Â
tF
∆
= .
Для полного описания канала в фиксированный момент
времени t
1
достаточно задать совместную плотность вероятно-
стей W(x, у) системы двух отсчетов, т.е. непрерывных случай-
ных величин X=X(t
1
) и Y=Y(t
1
). Часто для расчетов более удоб-
ными являются следующие характеристики:
W(x) – одномерная плотность вероятности сообщения,
W(y) – одномерная плотность вероятности сигнала,
W(x/y) – условная плотность вероятности сообщения х при
известном у,
W(y/x) – условная плотность вероятности сигнала у при за-
данном х.
Соотношения, связывающие эти плотности вероятности, см.
в разд. 1, формулы (1.3) – (1.5).
Обобщим понятие взаимной информации на непрерывные
сигналы.
Взаимная информация. По аналогии с дискретным случа-
ем взаимной информацией называют величину
()
(
)
() ()
()
()
()
()
,
;log
log log .
Wxy
Ixy
WxWy
Wxy Wyx
Wx Wy
==
=
(3.1.1)
Свойства взаимной информации I(х;у) для непрерывных
случайных величин х и у аналогичны свойствам взаимной ин-
=
45
формации I(x
j
;y
k
) для дискретных случайных величин, за исклю-
чением свойства 2, связанного с понятием собственной инфор-
мации, неприменимым к непрерывной случайной величине (см.
далее в разд. 3.2).
Средняя взаимная информация. Рассмотрим среднее зна-
чение взаимной информации для объединенного ансамбля XY.
Здесь возможны следующие случаи. Средняя информация, со-
держащаяся в реализации у принятого сигнала относительно
ансамбля передаваемых сообщений X, есть
()
(
)
()
()()
()
()
()
;Mlog ;
log .
WXy
I
Xy WxyIxydx
WX
Wxy
Wxy dx
Wx
∞
−∞
∞
−∞
== =
∫
∫
(3.1.2)
Иначе, это – средняя взаимная информация между ансамблем X
и реализацией у.
Средняя информация, содержащаяся в реализации переда-
ваемого сообщения x относительно ансамбля Y, равна
()
(
)
()
()()
()
()
()
;Mlog ;
log
WYx
I
Yx W yxI xydy
WY
Wyx
Wyx dy
Wy
∞
−∞
∞
−∞
== =
∫
∫
(3.1.3)
Это – средняя взаимная информация между ансамблем Y и
реализацией х.
Средняя информация о непрерывной случайной величине X,
заключенная в непрерывной случайной величине Y,
()
(
)
()
()
(
)
()
; M log , log
WXY Wxy
IXY Wxy dxdy
WX Wx
∞∞
−∞ −∞
==
∫∫
(3.1.4)
есть средняя взаимная информация между ансамблями X и Y.
Средняя взаимная информация неотрицательна, обладает
свойством симметрии и связана с относительными энтропиями
(см. разд. 3.2) непрерывных случайных величин X и Y следую-
=
=
46
щим образом:
(
)
(
)
(
)
(
)
(
)
;//.
I
XY H X H X Y HY HY X=− =−
(3.1.5)
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 3.1.1. Вольтметром измеряется напряжение в элек-
трической сети. Ошибка измерения не зависит от истинного
значения напряжения и распределена нормально с нулевым ма-
тематическим ожиданием и среднеквадратическим отклонени-
ем, равным 2 В. Истинное значение напряжения в сети также
имеет нормальное распределение с математическим ожиданием
220 В и СКО, равным 10 В.
Найти:
а) зависимость величины получаемой информации от пока-
заний прибора,
б) среднюю величину получаемой информации.
Решение. Введем обозначения:
X – напряжение в сети,
V – ошибка измерения,
Y = X + V – показание прибора.
Из условия задачи записываем плотности вероятностей:
()
()
2
2
1
exp ,
2
2
x
x
x
xm
Wx
σ
πσ
−
=−
()
()
2
2
1
exp .
2
2
v
v
yx
Wyx
σ
πσ
−
=−
Безусловную плотность вероятности величины Y можно
найти по общей формуле (1.3), но проще поступить следующим
образом. Показание прибора Y есть сумма двух независимых
нормальных случайных величин и, следовательно, Y также име-
ет нормальное распределение с математическим ожиданием
220 Â
yxvx
mmmm
=
+==
и дисперсией
222 2
104 Â
yxv
σσσ
=+= .
47
Итак,
()
()
2
2
1
exp .
2
2
x
y
y
ym
Wy
σ
πσ
−
=−
Условную плотность вероятности х находим по формуле
(1.4)
()
()
(
)
()
WyxWx
Wxy
Wy
==
()()()
222
22 2
2
1
exp .
2
22
y
xx
vx y
vx
yx xm ym
πσ
σσ σ
πσ πσ
−− −
−+−
В выражении, стоящем под знаком экспоненты, осуществ-
ляем возведение в квадрат и затем группируем члены, содержа-
щие х
2
и х. В итоге убеждаемся, что условное распределение ве-
личины х также нормально
()
()
2
2
1
exp ,
2
2
xSy
Wxy
δ
πδ
−
=−
где
() ()
2
2
x
xx
y
Sy m y m
σ
σ
=+ − – условное математическое
ожидание X,
22
2
2
xv
y
σ
σ
δ
σ
= – условная дисперсия X.
Для ответа на вопрос п. а) следует по формуле (3.1.2) вы-
числить величину средней взаимной информации между ан-
самблем X и реализацией у
()
()
()
;Mln
WXy
IXy
WX
==
()
()
2
2
22
Mln .
22
x
x
x
XSy
Xm
σ
δδ σ
−
−
−+
=
=
48
Находим квадраты разностей и выносим за знак математи-
ческого ожидания слагаемые и множители, не зависящие от х.
Далее учитываем, что вычисляются условные математические
ожидания при конкретном значении у, поэтому
[
]
(
)
(
)
22 2
M,M .XSy X Sy
δ
==+
В итоге получаем
()
2
2
2
22
11
;ln 1
22
y
xx
vyy
ym
IXy
σ
σ
σσσ
−
=
+−=
()
2
220
1 104 100
ln 1
2 4 2 104 104
y
−
+
−=
⋅
()
2
220
1,629 0,4801 1 í àò.
104
y
−
+−
Таким образом, искомая зависимость есть параболическая
функция разности
x
ym
−
, причем наименьшее количество ин-
формации, равное 1,1482 нат, доставляет наиболее вероятное
показание прибора
220
x
ym В
=
= .
Для ответа на вопрос п. б) необходимо найти среднюю ве-
личину взаимной информации между ансамблями X и Y. Вычис-
ляем безусловное математическое ожидание величины I(Х; у).
При этом учитываем, что
()
2
2
M
xy
Ym
σ
−
=
, и получаем
()
2
2
22
11
; ln ln 1 1,629 í àò.
22
y
x
vv
IXY
σ
σ
σσ
==+=
Обратите внимание, что в среднем количество получаемой
информации в данном примере зависит только от отношения
«сигнал/ошибка»
.
xv
σ
σ
Пример 3.1.2. Для контроля исправности блока периодиче-
ски измеряют значение напряжения в контрольной точке схемы.
Если блок исправен, то это напряжение равно 1 В, в противном
случае – 0 В. Ошибка вольтметра распределена равномерно с
=
=
49
нулевым математическим ожиданием, но ширина этого распре-
деления зависит от величины измеряемого напряжения: она
равна 2 В, если напряжение на входе 1 В, и 1 В − в противном
случае. В среднем в 90% времени блок исправен.
Найти количество информации, доставляемой прибором
при одном измерении.
Решение. Введем обозначения:
X – измеряемое напряжение, Y – показание вольтметра.
Из условия задачи следует, что величина X – двоичная,
причем
()
(
)
12 1 2
1; 0; 0,9; 0,1.x x px px== = =
Сигнал Y есть непрерывная случайная величина, и для нее
заданы условные плотности вероятности:
()
1
0,5, 0 2,
0, 0, 2,
y
Wyx
yy
≤≤
=
<>
()
2
1, 0, 5 0, 5,
0, 0,5, 0,5.
y
Wyx
yy
−≤≤
=
<− >
Рассматриваемый канал является дискретно-непрерывным,
так как входной сигнал дискретен, а выходной непрерывен.
Требуется найти среднюю взаимную информацию I(X;Y).
Найдем безусловную плотность вероятности выходного
сигнала:
()
(
) ()()
(
)
112 2
0, 0,5,
0,1, 0,5 0,
0,55, 0 0,5,
0, 45, 0,5 2,
0, 2 .
Wy pxWyx pxWyx
y
y
y
y
y
=
+=
<−
−≤<
≤≤
<≤
<
Далее вычисляем величину средней взаимной информации,
учитывая соотношение (3.1.3)
()
(
)( ) ( )
(
)
112 2
;; ;IXY pxIYx px IYx
=
+=
50
() ()
(
)
()
2
1
11
0
log
Wyx
p
xWyx dy
Wy
+
∫
() ()
(
)
()
0.5
2
22
0.5
log
Wyx
p
xWyx dy
Wy
−
=
∫
0,5
2
00,5
0,5 0,5
0,9 0,5 log 0,5 log
0,55 0, 45
dy dy
⋅
+⋅ +
∫∫
0,5
0
0,5 0
11
0,1 1 log 1 log 0,2809 áèò.
0,1 0,55
dy dy
−
⋅+⋅ =
∫∫
3.2 Относительная (дифференциальная) энтропия
Определения. Из формулы (2.2.3) видно, что даже в дис-
кретном случае при бесконечном числе состояний энтропия не
имеет верхней грани. Тогда неопределенность реализации одно-
го из бесконечного множества состояний (т.е. непрерывной слу-
чайной величины) может быть сколь угодно велика – непрерыв-
ные случайные величины не допускают введения конечной аб-
солютной меры неопределенности. Поэтому вводится относи-
тельная мера неопределенности – относительная энтропия
() () () ()
ä
Mlog log .H X WX Wx Wxdx
∞
−∞
=− =−
∫
(3.2.1)
Благодаря связи с дифференциальным законом распределе-
ния вероятностей ее называют еще дифференциальной энтропи-
ей (в дальнейшем изложении индекс д и слово «дифференци-
альная» будем опускать, но помнить, что если речь идет о не-
прерывной случайной величине, то ее энтропия Н(Х) есть вели-
чина относительная).
Аналогично для относительной энтропии непрерывной слу-
чайной величины Y имеем
() () ()
log .HY W y W ydy
∞
−∞
=−
∫
(3.2.2)
=
+
=
+

51
Для средней условной энтропии имеем
() () ()
,log ,HXY Wxy Wxydxdy
∞∞
−∞ −∞
=−
∫∫
(3.2.3)
() () ()
,log .HYX Wxy W yxdxdy
∞∞
−∞ −∞
=−
∫∫
(3.2.4)
Свойства. Энтропия непрерывных величин обладает свой-
ствами, во многом аналогичными свойствам энтропии дискрет-
ных случайных величин.
1) Относительная энтропия может принимать любые значе-
ния (сравнить с (2.2.2))
()
.HX
−
∞< <∞
(3.2.5)
2) Свойство аддитивности.
Энтропия объединения двух непрерывных случайных величин
()
(
)
(
)()
(
)
,HXY HX HYX HY HXY=+ =+
(3.2.6)
если X и Y статистически связаны между собой. Здесь обозначе-
но
() () ()
,log , .HXY Wxy Wxydxdy
∞∞
−∞ −∞
=−
∫∫
(3.2.7)
Энтропия объединения двух независимых непрерывных
случайных величин равна сумме их энтропий
(
)()()
.HXY HX HY=+
(3.2.8)
3) Относительная условная энтропия не превышает безус-
ловной
()
(
) ()
(
)
,.HXY HX HYX HY≤≤
(3.2.9)
4) Свойство экстремальности энтропии.
Среди всех непрерывных случайных величин, удовлетво-
ряющих условиям:
а)
() ()
,xW xdx
ϕ
θ
∞
−∞
=
∫
б)
()
1Wxdx
∞
−∞
=
∫
(условие нормировки),
(3.2.10)
52
наибольшей энтропией обладает случайная величина X, имею-
щая плотность вероятности
(
)
(
)
12
exp .Wx x
λ
ϕλ
=+
(3.2.11)
Коэффициенты λ
1
и λ
2
выбираются так, чтобы функция W(x)
удовлетворяла условиям а) и б).
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 3.2.1.
Положительная непрерывная случайная ве-
личина X распределена по экспоненциальному закону с матема-
тическим ожиданием m
х
=3. Вычислить значение дифференци-
альной энтропии величины X.
Решение. Заданный закон распределения имеет вид
()
1
exp
xx
x
Wx
mm
=
−
,
0.x ≥
Дифференциальная энтропия непрерывной случайной вели-
чины X определяется формулой (3.2.1)
() ()
1
M log M log exp
xx
x
HX Wx
mm
=
−=− −=
() ()
log log
log M log log .
xxxx
xx
ee
mXmmem
mm
+=+=
Подставляя m
x
= 3, получим
(
)
(
)
log 2,7183 3 3,0277 áèòHX=⋅= .
Пример 3.2.2. Среди всех случайных величин, которые мо-
гут принимать значения из интервала (а, в) и имеют следующие
числовые характеристики:
() () () ()
() ()
112 2
, ,...,
,
bb
àà
b
kk
à
xW xdx xW xdx
xW xdx
ψθψθ
ψθ
==
=
∫∫
∫
найти случайную величину X, обладающую наибольшей энтро-
=

53
пией.
Решение. Поставленная задача состоит в определении
плотности вероятности W(x), доставляющей наибольшее значе-
ние функционалу энтропии
( ) () ()
ln ,
b
a
HX Wx Wxdx=−
∫
при указанных k условиях и условии нормировки
() ()
11.
b
a
kWxdx
+
=
∫
Составляем вспомогательный функционал
() ()
1
1
,
k
ii
i
FX HX
λ
θ
+
=
=+
∑
где λ
j
– произвольные постоянные коэффициенты (неопределен-
ные множители Лагранжа). Так как сумма
1
1
k
ii
i
λ
θ
+
=
∑
есть по усло-
вию задачи величина постоянная, не зависящая от конкретного
вида функции W(x), то плотность W(x), обеспечивающая макси-
мум функционалу F(X), обеспечит также максимальное значе-
ние функционалу Н(Х).
Вспомогательный функционал с учетом выражений
(1) – (k+1) принимает вид
( ) () () ()
1
1
ln ,
b
k
ii
i
a
FX Wx Wx x dx
λψ
+
=
=−+
∑
∫
где
1
1
k
ψ
+
= .
Воспользуемся очевидным соотношением
() ()
{
}
ln exp
ii ii
x
x
λψ λψ
=
и получим
() ()
()
()
1
1
exp
ln
k
ii
b
i
a
x
FX Wx dx
Wx
λψ
+
=
=
⋅=
∑
∫
54
()
()
1
1
exp
Mln .
k
ii
i
X
WX
λψ
+
=
∑
Далее пользуемся неравенством Иенсена (см. пример 1.4) и
получаем
()
()
()
1
1
exp
ln M
k
ii
i
X
Fx
WX
λψ
+
=
≤
=
∑
()
()
()
()
1
1
1
1
exp
ln ln exp .
k
ii
bb
k
i
ii
i
aa
x
Wx dx x dx
Wx
λψ
λψ
+
+
=
=
=
∑
∑
∫∫
Правая часть этого неравенства есть постоянная, не завися-
щая от вида распределения W(x), поэтому наибольшее значение
F(x) будет достигнуто для функции W(x), обращающей неравен-
ство в равенство. Как следует из примера 1.4, неравенство Иен-
сена обращается в равенство только в том случае, когда
()
()
1
1
exp
,
k
ii
i
x
Ñ
Wx
λψ
+
=
=
∑
где С – некоторая постоянная.
Полагая С=1, получим
() ()
1
1
exp
k
ii
i
Wx x
λψ
+
=
=
∑
.
Подставляя эту функцию в выражения (1) – (k+1) и решая
систему k+l уравнений, можно найти конкретные значения ко-
эффициентов
12 1
,,, .
k
λ
λλ
+
K
Пример 3.2.3. Среди всех случайных величин, для которых
задано математическое ожидание m
х
, а W(x)=0 при х<0, найти
=
=

55
случайную величину X, обладающую наибольшей энтропией.
Решение. Задача состоит в нахождении плотности вероят-
ности W(x), доставляющей максимум функционалу энтропии
() () ()
lnHX Wx Wxdx
∞
−∞
=−
∫
при дополнительном условии
()
0
1)
x
x
Wx m
∞
=
∫
(3.2.12)
и условии нормировки
()
0
2) 1.Wxdx
∞
=
∫
Имеем решение задачи в
общем виде (формула (3.2.11))
(
)()
12
exp .Wx x
λ
ϕλ
=+
Сравнивая выражения (3.2.10) и (3.2:12), убеждаемся, что
()
x
x
ϕ
=
, и решение для данного случая примет вид
(
)
[
]
12
expWx x
λ
λ
=+.
Значения коэффициентов λ
1
и λ
2
ищем, подставляя W(x) в
условия (3.2.12). Получим систему уравнений с двумя неизвест-
ными:
12 12
00
1) , 2) 1.
xx
x
xe dx m e dx
λλ λλ
∞∞
++
==
∫∫
Решаем эту систему уравнений. Из уравнения 2) находим
∫
∞
=
0
1
2
1
dxe
e
x
λ
λ
.
Воспользуемся табличным интегралом вида
∫
∞
−=
0
1
c
dxe
cx
,
где с<0. Тогда
∫
∞
−=
0
1
1
1
λ
λ
dxe
x
и
1
2
λ
λ
−=e .
56
Подставляя
1
2
λ
λ
−=e в уравнение 1) системы
∫
∞
=−
0
1
)(
1
x
x
mdxxe
λ
λ
и воспользовавшись табличным интегралом вида
∫
∞
−=
0
2
1
c
dxxe
cx
,
получим
∫
∞
=
−
⋅−=−
0
2
1
11
)(
1
)()(
1
x
x
mdxxe
λ
λλ
λ
.
Отсюда
x
m
1
1
−=
λ
и
x
m
e
1
1
2
=−=
λ
λ
.
Искомый закон распределения имеет вид
12
1
() exp , 0.
x
xx
x
Wx e e x
mm
λλ
=
=− ≥
Это – одностороннее экспоненциальное распределение
3.3 Информационные характеристики непрерывных
случайных функций
Имеются два различных способа определения информации-
онных характеристик непрерывных стационарных случайных
функций.
Первый способ предусматривает квантование во времени
исходной непрерывной случайной функции X(t) и переход к по-
следовательности непрерывных случайных величин-отсчётов
…, X
)1(−
,X
)0(
,X
)1(
,…, взятых через интервалы
()
12tF
∆
=∆,
где
F
∆
– ширина полосы частот на положительной полуоси,
занимаемых спектром плотности мощности этой функции. Для
полученной непрерывной последовательности вводятся харак-
теристики, аналогичные тем, которые были введены для дис-
кретных последовательностей (формулы (2.4.1) – (2.4.3), (2.4.6)
– (2.4.10)), но используется понятие относительной энтропии.
57
Определённая таким образом энтропия непрерывной слу-
чайной величины функции X(t) равна средней относительной
энтропии, приходящейся на один отсчёт. Эта величина также
удовлетворяет неравенствам (2.4.3) и (2.4.4), причём в качестве
H
max1
используется максимальное значение относительной эн-
тропии непрерывной случайной величины при заданных ог-
раничениях. Например, если задана средняя мощность σ
2
слу-
чайной функции X(t), оба неравенства совместно дают
[]
)2log(
2
1
)(
2
σπ
etXH ≤ ,
(3.3.1)
причём максимальной относительной энтропией на один отсчёт
обладает нормальная случайная функция с нулевым математи-
ческим ожиданием, дисперсией (средней мощностью)
2
σ
и рав-
номерным в полосе F
∆
энергетическим спектром (белый шум).
«Энтропийной мощностью» случайной функции X(t),
имеющей ширину спектра
F∆
и энтропию Н нат/отсчёт, назы-
вается средняя мощность белого шума с такой же шириной
спектра и тем же значением энтропии на отсчёт
)12exp(
2
1
−= HN
π
.
(3.3.2)
Относительная энтропия на один отсчёт нормальной слу-
чайной функции, имеющей спектр плотности мощности G(f),
вычисляется по формуле
[] []
1
() ln 2 ( )
2
F
HXt e FGf df
F
π
∆
=⋅∆⋅
∆
∫
,
(3.3.3)
а энтропийная мощность равна
∆
−∆=
∫
∆F
dffG
F
FN )(ln
1
exp
.
(3.3.4)
Второй способ введения энтропийных характеристик слу-
чайной функции опирается на понятие точности воспроизведе-
ния реализации этой функции. Пусть x(t) есть реализация непре-
рывной случайной функции X(t), которую необходимо передать,
58
а z(t) – реализация другой случайной функции Z(t), которая в
действительности принимается. Обозначим как ),( ZX
ρ
неко-
торую заранее заданную количественную меру различия этих
двух случайных функций. Тогда
ε
-энтропией
[
]
)(tXH
ρ
ε
слу-
чайной функции X(t) называется минимальное среднее количе-
ство взаимной информации в единицу времени между X(t) и Z(t),
необходимое для того, чтобы
ε
ρ
≤
),( ZX .
Часто в качестве меры отличия используют среднеквадра-
тическую ошибку воспроизведения стационарной случайной
функции X(t) при помощи стационарной и стационарно свя-
занной с ней случайной функции Z(t)
2
0
(,) M( )XZ X Z
ρ
=−
.
(3.3.5)
Если Z(t) – это цифровой сигнал, то
ε
-энтропия численно
равна минимальному среднему количеству двоичных символов
в единицу времени, необходимых для восстановления функции
X(t) со среднеквадратической ошибкой, не превышающей
ε
.
Для нормальной стационарной случайной функции X(t),
имеющей спектр плотности мощности G(f),
ε
-энтропия при
среднеквадратическом критерии точности (3.3.5) вычисляется
по формуле
[]
0
()
() log
f
Gf
HXt df
ε
λ
∆
=
∫
,
(3.3.6)
где
f
∆
– полоса частот, в которой
λ
≥)( fG
. Коэффициент
λ
выбирается таким образом, чтобы площадь фигуры, ограничен-
ной снизу осью f, а сверху – прямой G=
λ
(в области f∆ ) либо
кривой G(f) (вне области f
∆
), была равна
2
ε
. Эта фигура за-
штрихована на рис. 3.3.1.
Понятие
ε
- энтропии может
быть применено и к последова-
тельности дискретных случайных
величин.
При вычислении
ε
-энтропии
случайной величины X, когда рас-
G(f)
f
λ
∆f
ε
2
Рис. 3.1
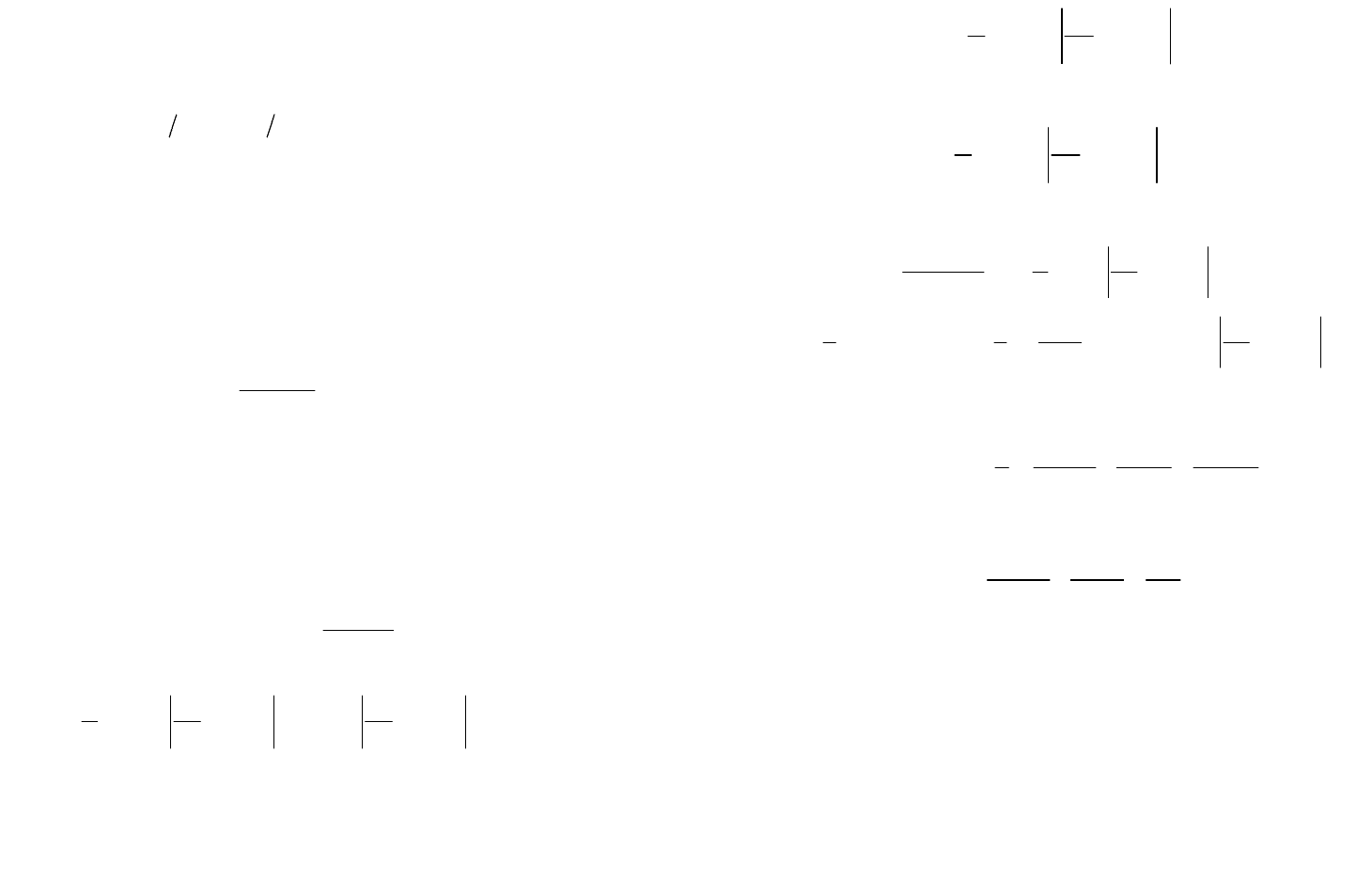
59
стояние между X и Z задано в виде математического ожидания
некоторой функции
[
]
(,) M ()
X
ZV
ρϕ
=
(3.3.7)
их разности V=X–Z, справедливо соотношение
()()()HXZ HVZ HV
=
≤ .
(3.3.8)
Оно показывает, что средняя условная энтропия ошибки
при заданном ограничении
ε
ρ
≤ достигает максимального
значения, когда X и Z независимы. Это требование, однако, не
является достаточным.
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 3.3.1. Нормальный стационарный узкополосный
случайный процесс, имеющий корреляционную функцию
τπ
τ
τ
0
22
2cos
1
1
)(
f
a
B
+
=
,
пропускают через идеальный фильтр с полосой, заключённой в
интервале частот от Fff −
=
01
до Fff
+
=
02
. Найти отно-
сительную энтропию в единицу времени для процесса на вы-
ходе фильтра.
Решение. Односторонний спектр плотности мощности ис-
ходного процесса в соответствии с теоремой Винера−Хинчина
равен преобразованию Фурье от корреляционной функции
0
22
1
() 2 ()cos2 2 cos2( ) .
1
Gf B fd f f d
a
τ
πττ π ττ
τ
∞∞
−∞ −∞
==−
+
∫∫
Этот интеграл – табличный:
00
22
() exp ( ) exp ( ) , 0.Gf f f f f f
aa a
ππ π
=−−+−+ ≥
Поскольку процесс узкополосен, то справедливо соотноше-
ние f
0
>>a, поэтому в полученном выражении можно пренеб-
речь вторым слагаемым и получим
60
0
2
() exp ( ), 0.Gf f f f
aa
ππ
≈
−− ≥
Спектр плотности мощности процесса на выходе идеально-
го полосового фильтра равен
01 2
2
() exp ( ), .
âû õ
Gf ff fff
aa
ππ
=
−− ≤≤
Величину относительной энтропии на один отсчёт вычис-
ляем по формуле (3.3.3)
[]
[]
2
1
2
1
0
21
2
21 21 0
12
() ln exp ( )
2( )
112 2
ln 2 ( ) ln ( ) ( ) .
22
f
f
f
f
HXt f f df
ff a a
e
ef f f f f f df
aa
ππ
ππ
π
=−−+
−
+−= −+−−
∫
∫
Далее учитываем, что
20 01
f
fffF
−
=−=и, осуществив
интегрирование, получим
22
14 2 íàò
[()] ln .
2îòñ÷¸ò
eF F
HXt
aa
ππ
=−
В одну секунду берется
FFn 42
=
∆
=
отсчётов, поэтому
относительная энтропия в единицу времени равна
22
48íàò
[()]2ln .
ñ
eF F
HXt F
aa
ππ
=−
Пример 3.3.2. Уровень воды в водоёме U(t) меняется со
временем так, что он полностью определяется отсчётами, взя-
тыми через полгода. Отдельные отсчёты независимы и имеют
одностороннее экспоненциальное распределение с математиче-
ским ожиданием, равным 4 м. При учёте запаса воды допустимы
только положительные ошибки v=u–z, причём среднее значение
ошибки не должно превышать 0,25 м.
Найти
ε
-энтропию функции U(t).
Решение. Задача заключается в вычислении минимального
среднего количества информации, которое необходимо пере-
давать в год для воспроизведения функции U(t) при помощи
другой функции с заданной точностью. За год уровень воды из-
