Акулиничев Ю.П., Дроздова В.И. Теория информации
Подождите немного. Документ загружается.


21
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 2.1.1. Определить собственную информацию, со-
держащуюся в изображении, при условии, что оно разлагается
на 500 строк по 500 элементов в каждой строке. Яркость каждо-
го элемента передается одним из восьми квантованных уровней.
Различные градации яркости равновероятны, а яркости разных
элементов статистически независимы.
Решение. Обозначим случайной величиной
X
яркость од-
ного элемента изображения. По условию задачи все 8 градаций
яркости одинаково вероятны, т.е. ()1
j
p
xn
=
, где 8n
=
и, сле-
довательно, собственная информация одного элемента для лю-
бого j по формуле (2.1.1)
2
()log
j
I
xn= .
Изображение содержит
5
500 500 2,5 10N =⋅=⋅ элементов.
Так как яркости элементов независимы, то по свойству ад-
дитивности информации
55
2
(èçî áðàæåí èÿ) ( ) log 2,5 10 3 7,5 10 áèò.
j
INIxNn== =⋅⋅=⋅
Пример 2.1.2. На экране индикатора РЛС, представляюще-
го поле с 10 вертикальными и 10 горизонтальными полосами,
появляется изображение объекта в виде яркостной отметки. Все
положения объекта равновероятны.
Определить количество информации, содержащееся в со-
общениях:
а) объект находится в 46-м квадрате экрана;
б) объект находится в 5-й горизонтальной строке экрана;
в) объект находится в 6-м вертикальном столбце и 3-й гори-
зонтальной строке экрана.
Решение. а) Пусть
46
x
– сообщение о том, что объект нахо-
дится в 46-м квадрате экрана.
Собственная информация в этом сообщении по формуле
(2.1.1) равна
46 2 46
() log()
I
xpx
=
− . Безусловная вероятность
сообщения – объект находится в 46-квадрате экрана – равна
46
()
p
xmn= , где n – общее число возможных исходов (квад-
22
ратов поля), m – число исходов, благоприятствующих событию
46
x
.
По условию задачи 100n
=
квадратов, a 1m
=
. Тогда
46
()0,01px
=
и
46 2
( ) log0,01 log 100 6,6439 áèò.Ix
=
−= =
б) Вероятность события
5
y – объект находится в 5-й гори-
зонтальной строке экрана – по аналогии с рассмотренным слу-
чаем а) определится
5
( ) 10 100 0,1py mn
=
== и собственная
информация
52 2
( ) log 0,1 log 10 3,3219 áèò.Iy
=
−==
в) Вероятность события
6,3
z – объект находится в 6-м вер-
тикальном столбце и 3-й горизонтальной строке – равна
6,3
() 0,01pz mn
=
= , следовательно,
6,3 2
( ) log 0,01 6,6439 áèò.Iz
=
−=
Пример 2.1.3. Рассматривается ансамбль сообщений, при-
веденный в
табл. 2.1.1.
Таблица 2.1.1
j
x
0
x
1
x
2
x
3
x
4
x
5
x
6
x
()
j
p
x
1/2 1/4 1/8 1/32 1/32 1/32 1/32
Кодовое
слово
001 010 100 011 101 110 111
Сообщение
4
x
поступает в кодер. Вычислить дополнитель-
ную информацию об этом сообщении, доставляемую каждым
последующим символом на выходе кодера.
Решение. На вход кодера поступает одно из сообщений
0
x
,...,
6
x
, а кодер порождает соответствующие таблице двоич-
ные символы. Так, сообщению
4
x
соответствует на выходе ко-
довое слово 101. Символы на выходе кодера появляются после-
довательно, т.е. первый символ 1, второй 0 и третий 1. Первый
символ кодового слова содержит некоторую информацию отно-
сительно того, какое сообщение поступает на вход кодера. Так,

23
первый символ 1 показывает, что на входе могли быть сообще-
ния
2
x
,
4
x
,
5
x
или
6
x
. Второй символ 0 сужает выбор – теперь
на входе возможно одно из двух сообщений:
2
x
или
4
x
. И, на-
конец, последний, третий символ 1 однозначно определяет пе-
реданное сообщение.
По формуле (2.1.3) взаимная информация, содержащаяся в
первом кодовом символе 1 относительно сообщения
4
x
, равна
4
4
4
(/1)
(;1)log
()
px
Ix
p
x
=
.
Обратная вероятность
4
(/1)px может быть найдена по
формуле Байеса (1.4)
44
4
6
1
()(1/ )
(/1)
(1 / ) ( )
jj
j
px p x
px
p
xpx
=
=
∑
,
где
1, 2,4,5,6,
(1 / )
0, 0,1,3,
j
j
px
j
=
=
=
т.е. условная вероятность (1 / ) 0
j
px= для гипотез, при которых
первый кодовый символ есть 0, и (1 / ) 1
j
px
=
для гипотез, при
которых первый кодовый символ 1. В знаменателе формулы
Байеса таким образом учитываются те гипотезы, при которых
возможно появление 1 на первом месте.
Итак,
4
132 1
(/1)
18 3132 7
px ==
+⋅
,
4
132 1
( /10)
18 132 5
px
=
=
+
,
4
132
( /101) 1
132
px
=
= ,
а взаимная информация, содержащаяся в первом кодовом сим-
воле 1 относительно сообщения
4
x
, равна
4
4222
4
(/1) 17
( ;1) log log log 32 log 7 2,1926 áèò.
() 132
px
Ix
px
===−=
24
Информация, содержащаяся во втором кодовом символе 0
при условии, что первый кодовый символ был 1, есть
4
42
4
( /10) 1 5
( ;0 /1) log log 0,4854 áèò.
(/1) 17
px
Ix
px
===
Информация, содержащаяся в третьем кодовом символе 1
при условии, что ему предшествовали 10, есть
4
42 2
4
( /101)
1
( ;1/10) log log 2,3219 áèò.
( /10) 1 5
px
Ix
px
===
Так как сообщения
J
x
и кодовые слова однозначно связа-
ны, то
44 4 4
() (;1) (;0/1) (;1/10)Ix Ix Ix Ix
=
++ .
Действительно,
4242
( ) log ( ) log 32 5Ix px
=
−== бит, и
это совпадает с приведенной суммой.
Пример 2.1.4. По дискретному каналу передаются сообще-
ния
1
x
или
2
x
. Вследствие действия шумов на выходе появляет-
ся один из сигналов
123
,,yyy. Вероятности совместного появ-
ления (; )
jk
p
xy заданы табл. 2.1.2
Вычислить взаимные информации
22
(; )
I
xy,
13
(; )
I
xy .
Решение. Дискретный канал с шу-
мом удобно изображать в виде графа
(рис. 2.1.2).
Определим взаимную информа-
цию по формуле (2.1.3)
13
13
1
(/ )
(; ) log
()
p
xy
Ix y
px
=
или в силу свойства симметрии
31
13 31
3
(/)
(; ) (;) log
()
p
yx
Ix y Iy x
py
==
.
Условные и безусловные вероят-
ности найдем, воспользовавшись таб-
лицей. По формуле (1.3)
Таблица 2.1.2
k
y
j
x
1
y
2
y
3
y
1
x
1/4 1/16 1/8
2
x
1/8 3/16 1/4
Рис. 2.1

25
1111213
1117
() (, ) (, ) (, )
416816
px px y px y px y=++=++=
;
2
1319
()
816416
px
=
++=
;
1
113
()
488
py
=
+=
;
2
131
()
16 16 4
py
=
+=;
3
113
()
848
py
=
+=.
Используя формулы (1.4), найдем условные вероятности:
22
22
2
(, )
316 1
(/)
() 916 3
px y
py x
px
===
,
13
13
3
(, )
18 1
(/)
() 38 3
px y
px y
py
===
.
Тогда количество взаимной информации по формуле (2.1.3)
22
22 2 2
2
(/)
13
( ; ) log log 0,415 áèò.
() 14
py x
Ix y
py
===
13
13 2 2
1
(/ )
13
( ; ) log log 0,3923 áèò.
() 716
px y
Ix y
px
===−
Мы получили
13
(; ) 0Ix y < , так как
13 1
(/ ) ()
p
xy px
<
.
2.2 Средняя собственная информация (энтропия)
Энтропия. Дискретный источник удобнее характеризовать
количеством собственной информации, содержащимся в сред-
нем в одном символе ансамбля X.
Это среднее количество собственной информации есть
() ()
()()
1
Mlog
n
jj
j
IX pX Ix px
=
=− = =
∑
1
()log() ()
n
jj
j
p
xpxHX
=
−=
∑
(2.2.1)
и названо энтропией (по аналогии с понятием энтропии в тер-
модинамике).
=
26
Свойства энтропии.
1) Энтропия неотрицательна
()0.HX ≥
(2.2.2)
Знак равенства имеет место, когда X – неслучайна, т.е. p(x
j
) = 1, a
p(x
i
) = 0 для .ij
≠
При этом неопределенность относительно ан-
самбля X отсутствует. Таким образом, энтропия есть мера неоп-
ределенности случайного ансамбля.
2) Величина энтропии удовлетворяет неравенству
()log.HX n
≤
(2.2.3)
Знак равенства имеет место при равновероятности символов
ансамбля X, т.е. при ()1.
j
p
xn
=
3) Свойство аддитивности энтропии.
В последовательности i независимых символов энтропия
равна сумме энтропий, содержащихся в отдельных символах
(1) ( ) (1) ( )
,..., ( ) ... ( ).
ii
HX X HX HX
=++
(2.2.4)
Вычисление энтропии по формуле (2.2.1) можно упростить,
введя функцию () log ,
p
p
η
=
− тогда формула примет вид
1
() ( ).
n
j
j
HX p
η
=
=
∑
(2.2.5)
Значения функции ()
p
η
приведены в Приложении 1.
Условная энтропия. Пусть имеются два статистически за-
висимых конечных ансамбля символов X и Y. Пары символов
x
j
y
k
c вероятностями p(x
j
, у
k
) можно рассматривать как элемен-
тарные символы объединенного ансамбля XY с энтропией
,,
11
() ( )log( ).
nm
jk jk
jk
HXY pxy pxy
==
=−
∑∑
(2.2.6)
Появление символа x
j
вызовет появление символа y
k
с ус-
ловной вероятностью
,
()
(/) .
()
jk
kj
j
p
xy
py x
px
=
При этом условная энтропия ансамбля Y в предположении,
что выбран символ х
j
, будет

27
1
(/ ) M log(/ )
(/)log(/).
jj
m
kj kj
k
HY x pY x
p
yx pyx
=
=− =
∑
(2.2.7)
Здесь каждому х
j
соответствует свое значение энтропии
(/ )
j
HY x , т.е. (/ )
j
HY x – случайная величина.
Тогда средняя условная энтропия случайной величины Y,
вычисленная при условии, что известно значение другой слу-
чайной величины X, равна
[]
1
11
(/ ) M log(/ ) () (/ )
() (/)log(/).
n
jj
j
nm
jkj kj
jk
HY X pY X px H Y x
px py x py x
=
==
=− = =
−
∑
∑∑
(2.2.8)
Энтропия объединенного ансамбля ()HXY удовлетворяет
следующим соотношениям:
а) () () (/) () (/),HXY HX HY X HY HXY=+ =+
(2.2.9)
если X и Y зависимы;
в) () () (),HXY HX HY
=
+
(2.2.10)
если X и Y независимы.
Для объединенного ансамбля XY условная энтропия удовле-
творяет неравенствам:
(/ ) (), ( /) ().HY X HY H X Y H X
≤
≤
(2.2.11)
Избыточность. Считают, что имеется избыточность, если
количество информации, содержащейся в сигнале (энтропия
сигнала), меньше того количества, которое этот сигнал мог бы
содержать по своей физической природе. Введем количествен-
ную меру избыточности. Пусть сигнал длиной в n символов (от-
счетов) содержит количество информации Н. Пусть далее наи-
большее количество информации, которое в принципе может
содержаться в данном сигнале с учетом наложенных на него ог-
раничений (заданное основание кода, заданная средняя мощ-
ность сигнала и т.п.), равно H
max
. Тогда количественной мерой
избыточности является величина
=
=
28
1
max
RHH
=
− .
(2.2.12)
Причины появления избыточности – это статистическая
связь между символами (отсчетами) сигнала и неэкстремаль-
ность распределения вероятностей отдельных символов (отсче-
тов). Введение избыточности приводит к удлинению сигнала, но
зато повышает его информационную устойчивость при воздей-
ствии помех.
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 2.2.1. На измерительной станции имеются два прибо-
ра. Первый имеет шкалу, содержащую 100 делений, его показания
могут меняться через каждые 0,05 с. Шкала второго прибора имеет
10 делений, и его показания могут меняться каждые 0,01 с.
Какова наибольшая средняя информация, поставляемая
двумя приборами в 1 с?
Решение. 1-й прибор. Энтропия одного значения (отсчета)
по формуле (2.2.3)
11
( ) log log 100.HX m
=
=
Число отсчетов в 1 секунду равно
1
1 0,05 20.n
=
=
2-й прибор. Энтропия одного значения
2
()log10HX
=
, а
число отсчетов в 1 секунду равно
2
100.n
=
Энтропия двух приборов в 1 с по формуле (2.2.4.) равна
11 2 2
( ) ( ) ( ) 20 6,64 100 3,32 465 áèò/ñ.HX nHX nHX
Σ
=
+=⋅+⋅≈
Пример 2.2.2. Производится стрельба по двум мишеням, по
одной сделано 2 выстрела, по второй – 3. Вероятности попада-
ния при одном выстреле соответственно равны 1/2 и 1/3. Исход
стрельбы (число попаданий) по какой мишени является более
определенным?
Решение. Исход стрельбы определяется числом попаданий
в мишень, которое подчинено биномиальному закону распреде-
ления
() (1)
m
mnm
n
pX m C p p
−
== − ,
где
!
!( )!
m
n
n
C
mn m
=
−
.
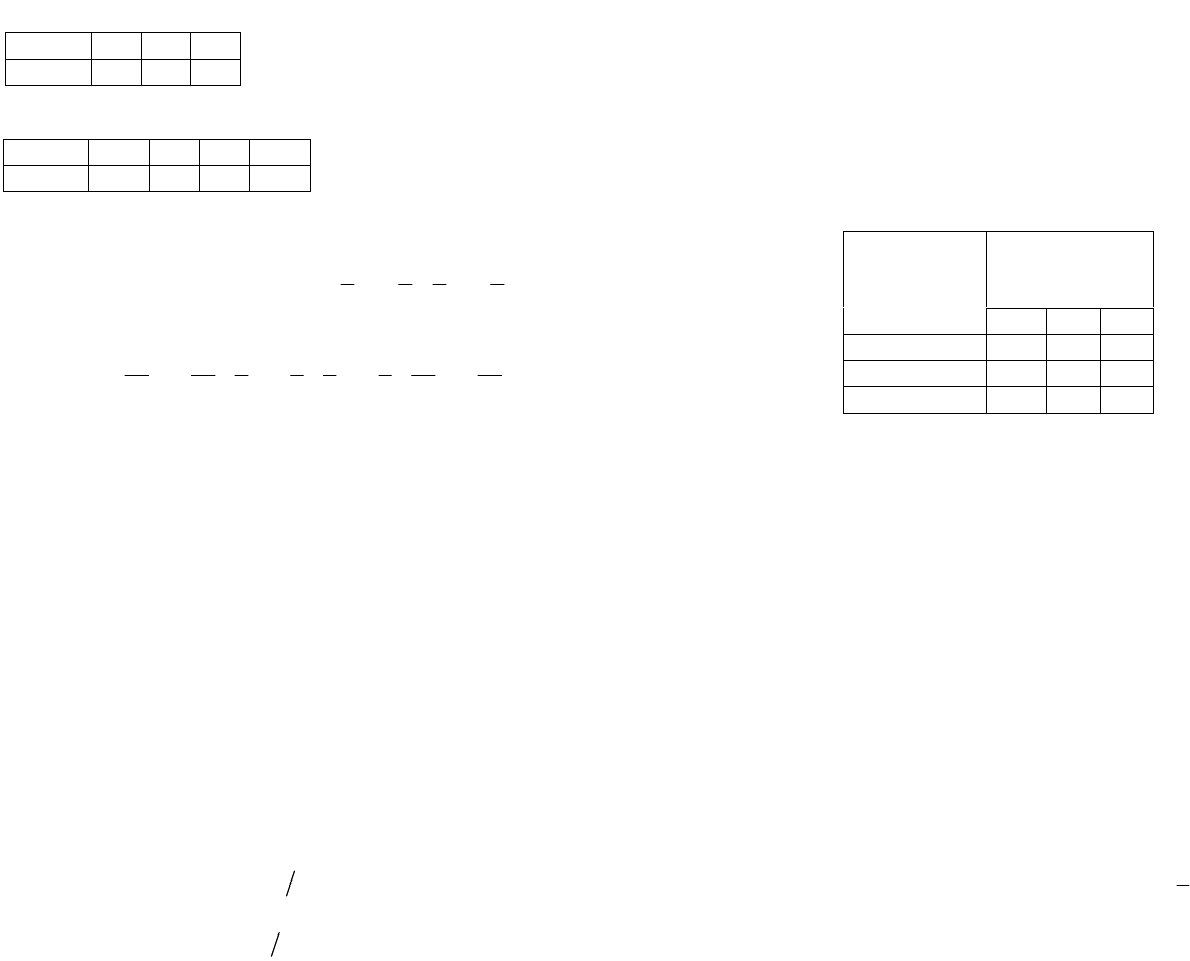
29
Составляем ряд распре-
деления для числа попаданий
в первую мишень при n=2 и
p=1/2 (табл. 2.2.1) и вторую
мишень при n=3 и p=1/3
(табл. 2.2.2).
Мерой неопределенно-
сти исхода стрельбы служит
энтропия числа попаданий.
Энтропия числа попаданий при стрельбе по первой мишени
1
122
1
1111
() ()log() 2 log log 1,5áèò.
4422
n
jj
j
HX px px
=
=− =− ⋅ + =
∑
Аналогично для второй мишени имеем
22222
8 844221 1
( ) log log log log 1,7 áèò,
27 27 9 9 9 9 27 27
HX
=− + + + =
т.е. исход стрельбы по второй мишени обладает большей неоп-
ределенностью.
Пример 2.2.3. Источник сообщений вырабатывает ан-
самбль символов
12 3 45 6
0,4 0,2 0,15 0,1 0,1 0,05
x
xxxxx
X
=
.
Символы в последовательности независимы.
Вычислить энтропию источника и определить избыточ-
ность.
Решение. Энтропия источника для случая неравновероят-
ных и независимых сообщений определяется формулой (2.2.1)
1
( ) ( ) log ( ) [0, 4 log 0, 4 0, 2 log 0,2
0,15 log 0,15 2 0,1 log 0,1 0,05 log 0,05] 2,2842 áèò.
m
jj
j
HX px px
=
=− =− ⋅ + ⋅ +
⋅+⋅⋅+⋅ =
∑
Избыточность за счет неоптимальности (неравновероятно-
сти) распределения сообщений в источнике определяется
формулой (1.2.12) 1
max
RHH
=
− , где log
max
Hm
=
по фор-
муле (2.2.3).
Отсюда 1 2,2842 log6 0,1164.R
=
−=
Таблица 2.2.1
m
0 1 2
p(x=m) 1/4 1/2 1/4
Таблица 2.2.2
m
0 1 2 3
p(x=m) 8/27 4/9 2/9 1/27
+
30
Пример 2.2.4. Алфавит источника состоит из трех букв:
х
1
, х
2
, х
3
.
Определить энтропию на 1 букву текста
(1)
X
,
(2)
X
для
следующих случаев:
а) буквы алфавита неравновероятны:
1
() 0,5px =
,
23
() ()0,25px px
=
= , а символы в последовательности на вы-
ходе источника статистиче-
ски зависимы. Условные ве-
роятности
(2) (1)
(/)
ji
p
xx за-
даны в табл. 2.2.3;
б) вероятности букв те
же, что и в п. а), но символы
независимы;
в) символы в последова-
тельности независимы, веро-
ятности букв одинаковы.
Вычислить избыточность источников для случаев а) и б).
Решение. а) В случае неравновероятных и зависимых со-
общений энтропия текста по формуле (2.2.9)
(1) (2) (1) (2) (1)
()()(/)HX X HX HX X=+ ,
где
(1)
1
() ()log()1,5áèò
m
jj
j
H X px px
=
=− =
∑
,
а условная энтропия по формуле (2.2.8) равна
33
(2) (1) (1) (2) (1) (2) (1)
11
(1) (2) (1) (2) (1) (2) (1) (2) (1)
111 11 21 21
(/) ()(/)log(/)
()(/)log(/)(/)log(/)
{[
iji ji
ij
HX X px px x px x
px px x px x px x px x
==
=− =
−
++
∑∑
(2) (1) (2) (1) (1) ( 2) (1) (2) (1)
31 31 2 12 12
(2) (1) (2) (1) (2) (1) (2) (1)
22 22 32 32
(/)log(/) ()(/)log(/)
(/)log(/)(/)log(/)
][
]
px x px x px px x px x
px x px x px x px x
+
+
++
(1) (2) (1) (2) (1) (2) (1) (2) (1)
313 13 23 23
(2) (1) (2) (1)
33 33 2 2
()( / )log( / )( / )log( / )
1
(/)log(/) 0,4log0,40,2log0,2
2
[
]} { [
px px x px x px x px x
px x px x
+
++
=−⋅+⋅+
Таблица 2.2.3
j – индекс по-
следующей
буквы
i – индекс
предыдущей
буквы
1 2 3
1 0,4 0,2 0,4
2 0 0,6 0,4
3 0,3 0 0,7
=
+
+
+

31
2222
2
11
0, 4 log 0, 4 0 0, 6 log 0,6 0, 4 log 0, 4 0,3 log 0,3
44
0,7 log 0,7 1,224 áèò.
][ ][
]}
⋅++⋅+⋅+⋅+
⋅≈
Энтропия на один символ
(1) (2) (1) ( 2) (1)
1
( , ) ( ) ( / ) 2 1,362 áèò ñèì â.HX X HX HX X
=+ =
б) При неравновероятных, но зависимых сообщениях эн-
тропия вычисляется по формуле (2.2.1)
22
1
1111 áèò
( ) ( )log ( ) log 2 log 1,5 .
2244 ñèìâ
n
jj
j
HX px px
=
=− =− + ⋅ =
∑
Избыточность, обусловленная статистической зависимо-
стью
11
1 ( ) ( ) 1 1,362 1,5 0,092.RHXHX=− =− =
в) В случае равновероятных и независимых сообщений эн-
тропия по формуле (2.2.3)
22
( ) log log 3 1,585 áèò.
max
HX m
=
==
Избыточность, обусловленная неоптимальностью распре-
деления
2
1 ( ) ( ) 1 1,5 1,585 0,054.
max
RHXHX=− =− =
Полная избыточность (за счет неоптимальности распреде-
ления и наличия статистических взаимосвязей)
1
1 ( ) ( ) 0,141.
max
RHXHX
=
−=
2.3 Средняя взаимная информация
Определения. В изучении проблем связи, кроме рассмот-
ренных выше величин, важную роль играет среднее значение
взаимной информации между элементами различных ансамблей.
Рассмотрим условное среднее значение взаимной информа-
ции для объединенного ансамбля XY. Пусть сигнал принял зна-
чение у
k
. Тогда информация, содержащаяся в реализации у
k
при-
нятого сигнала относительно ансамбля передаваемых сообще-
ний X,
+
+
32
1
1
(/)
(; ) Mlog ( / )(; )
()
(/)
(/)log
()
n
k
kjkjk
j
n
jk
jk
j
j
pX y
IXy px y Ix y
pX
px y
px y
px
=
=
=
==
−
∑
∑
(2.3.1)
есть средняя взаимная информация между ансамблем X и
реализацией y
k
.
Аналогично информация, содержащаяся в ансамбле приня-
тых сигналов Y относительно реализации переданного сообще-
ния x
j
, определяется как
1
1
(/ )
(;)Mlog ( / )(; )
()
(/)
(/)log .
()
m
j
jkjjk
k
m
kj
kj
k
k
pY x
Ix Y py x Ix y
pY
py x
py x
py
=
=
=
==
∑
∑
(2.3.2)
Это средняя взаимная информация между ансамблем Y и реали-
зацией x
j
.
Средняя взаимная информация между ансамблем прини-
маемых сигналов Y и ансамблем передаваемых сообщений X
1
11
(/)
(;) Mlog ()(; )
()
(/)
(, )log
()
k
kk
k
nm
jk
jk
jk
j
pX Y
IXY py IXy
pX
px y
px y
px
=
==
=
==
∑
∑∑
(2.3.3)
есть то количество информации, которое содержится в среднем
в ансамбле принимаемых символов Y относительно ансамбля
передаваемых символов X.
Основные свойства средней взаимной информации.
1) Средняя взаимная информация симметрична
(;) (;).
I
XY IYX
=
(2.3.4)
2) Средняя взаимная информация не превышает собствен-
ную
=
=
=

33
()
(;)
().
HX
IXY
HY
≤
(2.3.5)
3) Средняя взаимная информация всегда неотрицательна
(;)0.IXY ≥
(2.3.6)
4) Следующее свойство устанавливает соотношение между
средней взаимной информацией и энтропиями, относящимися к
объединенному ансамблю. Величина
(;) () ( /)
I
XY HX HXY
=
−
(2.3.7)
– среднее количество информации о сообщении, содержащееся
в принятом сигнале – равна среднему количеству информации,
требуемому для определения сообщения X, минус среднее коли-
чество информации, которое все еще потребуется для определе-
ния X после приема сигнала Y. Тогда энтропию Н(Х) мы пони-
маем как среднее количество переданной информации, а услов-
ную энтропию H(X/Y) – как среднее количество информации,
потерянное вследствие влияния шума («ненадежность»).
В другом варианте
(;) () (/ )
I
XY HY HY X
=
−
(2.3.8)
среднее количество информации есть разность между средним
количеством информации, необходимым для определения при-
нятого сигнала, и средним количеством информации, необходи-
мым для определения того же сигнала, когда известно передан-
ное сообщение. Тогда H(Y/X) можно трактовать как среднее ко-
личество информации, необходимое для определения помехи в
канале, т. е. это есть энтропия шума в канале.
При отсутствии в канале помех
(;) ()
I
XY HX=
,
(2.3.9)
т.е. принимаемый сигнал Y доставляет получателю всю инфор-
мацию, содержащуюся в переданном сигнале.
В этом случае у
k
и x
j
связаны однозначно
1ïðè ,
(/)
0ïðè ,
ji
ij
px y
ij
=
=
≠
(2.3.10)
и условная энтропия H(X/Y)=0.
При значительном уровне помех прием у
k
не дает ответа от-
носительно переданного x
j
, следовательно, X и Y можно при-
34
ближенно считать статистически независимыми, тогда
(/) ()
jk j
p
xy px
=
– прием символа у
k
никак не определяет пе-
реданного символа x
j
– и среднее количество информации
(;) () ( /) 0IXY HX HX Y
=
−=.
Очевидно, формулы (2.3.3), (2.3.7) и (2.3.8) дают тождест-
венные результаты, и выбор той или иной формулы при реше-
нии конкретной задачи производится из соображений удобства
математических выкладок.
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Пример 2.3.1. Вычислить для конкретного канала, заданно-
го в примере 2.1.4, средние количества информации.
11
( ; ), ( ; ), ( ; ).
I
Xy IxY IXY
Решение. а) Средняя взаимная информация в реализации
сигнала на выходе y
1
относительно случайной величины X на
входе канала определяется формулой (2.3.1)
1
11
1
11 21
11 21
12
(/)
(;) ( / )log
()
(/) (/)
( / )log ( / )log .
() ()
n
j
j
j
j
px y
IXy px y
px
p
xy pxy
px y px y
px px
=
==
+
∑
Из примера 2.1.4 известны вероятности:
12
() 716, () 916,px px
=
=
123
( ) 38, ( ) 14, ( ) 38.py py py
=
==
Определим условные вероятности:
11
11
1
(, )
14 2
(/) ,
() 38 3
px y
px y
py
=
==
21
21
1
(,) 18 1
(/) .
() 38 3
px y
px y
py
=
==
Средняя информация
12 2
223113
( ; ) log log 0,4967 áèò.
338338
IXy =+=
=
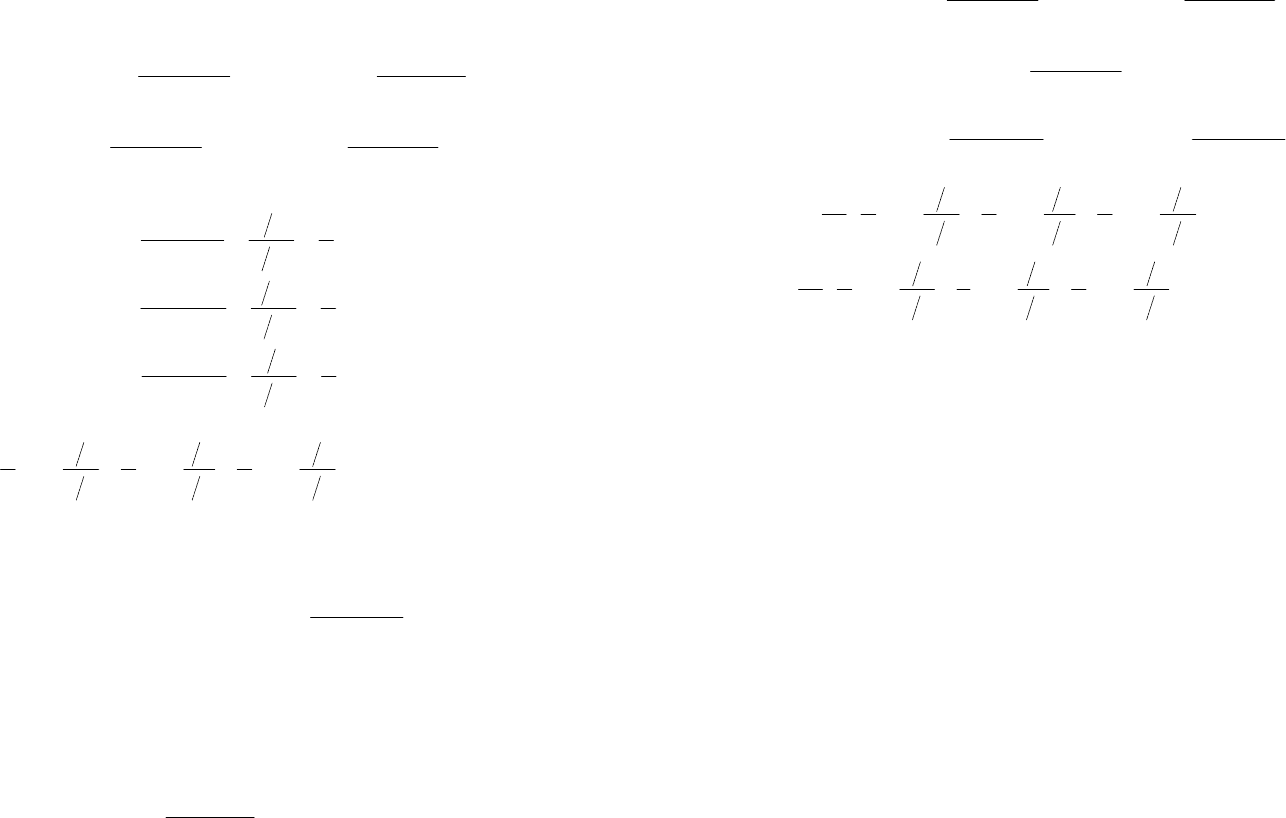
35
б) Средняя взаимная информация в выходной величине
Y относительно реализации случайной величины на входе x
1
определяется формулой (2.3.2)
1
11
11 11
1
1
31
21
21 31
23
(/)
(/)
(;) ( /)log (/)log
() ()
(/)
(/)
( / ) log ( / )log .
() ()
m
k
k
k
k
py x
py x
IxY py x py x
py py
py x
py x
py x py x
py py
=
==+
+
∑
Определяем условные вероятности
11
11
1
(, )
14 4
(/) ,
() 716 7
px y
py x
px
===
12
21
1
(, ) 116 1
(/) ,
() 716 7
px y
py x
px
===
13
31
1
(, )
18 2
(/) .
() 716 7
px y
py x
px
===
Условная средняя взаимная информация равна
12 22
447117227
( ; ) log log log 0,1198 áèò.
738714738
IxY =++=
в) Средняя взаимная информация между случайной
величиной Y на выходе канала и случайной величиной X на
входе определяется формулой (2.3.3)
11
(/)
(;) ()( / )log .
()
nm
kj
jkj
jk
k
p
yx
IXY px py x
py
==
=
∑∑
Воспользовавшись результатами вычислений
1
(;)
I
xY, по-
лучим для средней взаимной информации
1
11
111
1
(;) M (;) ()(;)
(/)
() ( / )log
()
[
n
jjj
j
I
XY Ix Y px Ix Y
py x
px py x
py
=
== =
+
∑
+
=
36
31
21
21 31
23
12
212
1
(/)
(/)
( / ) log ( / )log
() ()
(/)
() (/ )log
()
]
[
py x
py x
py x py x
py py
py x
px py x
py
+
+
++
32
22
22 32
23
222
(/)
(/)
( / )log ( / )log
() ()
7 4 47 1 17 2 27
log log log
16738714738
]
py x
py x
py x py x
py py
+
=
++ +
222
9 2 29 1 13 4 49
log log log 0,0972 áèò.
16938314938
++ =
Пример 2.3.2. На вход приемника двоичных сигналов по-
ступают посылки (1) и паузы (0). Априорные вероятности
р(0)=р(1)=1/2. Из-за помех посылка, появившаяся на входе при-
емника, регистрируется в решающем устройстве правильно (как
посылка) с вероятностью
0,8
α
=
, ошибочно (как пауза) – с ве-
роятностью
1.
α
−
При поступлении паузы на вход приемника
она принимается правильно (как пауза) с вероятностью
0,6
β
=
и ошибочно (как посылка) – с вероятностью
1
β
−
. Определить
среднюю информацию о входном сигнале, содержащуюся в на-
блюдаемом сигнале на выходе приемника.
Решение. Обозначим X – ансамбль сигналов на входе, Y –
ансамбль сигналов на выходе. Ищем среднюю взаимную ин-
формацию по формуле (2.3.8)
(;) () (/ ),
I
XY HY HY X
=
−
где
2
1
() ( )log ( )
kk
k
HY py py
=
=−
∑
– энтропия на выходе,
22
11
(/) ()(/)log(/)
jkj kj
jk
HY X px py x py x
==
=−
∑∑
– средняя
условная энтропия шума в канале, определяемая условными
вероятностями искажений
(/)
kj
p
yx. По условию задачи они
=
+
+
+

37
имеют следующие значения
0
1
() 0,8, ()1 0,2,
11
0
1
() 0,6, ()1 0,4.
00
pp
pp
αα
ββ
== =−=
== =−=
Для вычисления вероятностей появления сигналов на вы-
ходе p(Y=1) и p(Y=0) воспользуемся формулой полной вероят-
ности
11
(1) (1)( )(0)( )
10
0,50,8 0,50,4 0,6.
yy
py px p px p
xx
==
== =⋅ + =⋅ =
==
⋅+⋅=
00
(0)(0)( )(1)( )
01
0,5 0, 6 0,5 0, 2 0, 4.
yy
py px p px p
xx
==
== = + =⋅ =
==
⋅+⋅=
Тогда средняя взаимная информация
(;) () (/ )
(0)log(0)(1)log(1)
IXY HY HY X
py py py py
=− =
−=⋅ =−=⋅ =+
00
(0)[( )log( )
00
11
()log()]
00
yy
px p p
xx
yy
pp
xx
=
=
=
+
==
==
+
==
00
(1)[( )log( )
11
11
()log()]
11
yy
px p p
xx
yy
pp
xx
=
=
=
+
==
==
=
==
[]
[]
22
22
0, 4 log 0, 4 0, 6log 0,6
0,5 0,6 log 0,6 0, 4 log 0, 4
{
−⋅ + +
⋅
+⋅ +
[]
22
0,5 0,2 log 0,2 0,8 log 0,8 0,1245 áèò.
}
⋅+⋅ =
Пример 2.3.3. Эргодический источник имеет алфавит, со-
стоящий из 8 букв. Средние частоты повторения букв одинако-
вы. При передаче по каналу с шумом в среднем половина всех
букв принимается правильно, в другой половине случаев имеют
место ошибки, при этом любая буква переходит в любую дру-
=
=
+
+
+
+
=
+
+
38
гую с одинаковой вероятностью. Какова средняя информация в
принятой букве относительно переданной?
Решение. Обозначим
123 8
123 8
...
( ) ( ) ( ) ... ( )
xxx x
X
p
xpxpx px
=
–
ансамбль переданных букв,
123 8
123 8
...
() () ()... ()
yyy y
Y
p
ypypy py
=
–
ансамбль принятых букв.
Так как для эргодической последовательности средние по
времени частоты повторения букв совпадают с вероятностями,
то по условию задачи вероятности появления букв на входе
канала
()1 18.
j
px n
=
=
Ищем условные вероятности (/)
kj
p
yx. Поскольку по-
ловина всех букв принимается правильно, то
(/)1/2
kj
py x =
при .kj
=
Другая половина случаев есть ошибочный прием, причем
по условию задачи все возможные ошибки равновероятны.
Число возможных переходов (ошибок) равно 7. Тогда веро-
ятность ошибки (/)0,51/71/14
kj
py x
=
⋅= при .kj
≠
Вероятности появления букв на выходе найдем по (1.3)
8
1
11 1 1 1
() ()( /) 7
82 814 8
kjkj
j
py px py x
=
=
=⋅+⋅⋅ =
∑
для любого к.
Этот же результат следует непосредственно из того факта,
что рассматриваемый канал – симметричный (набор вероятно-
стей ошибок одинаков для любого Х), тогда при равномерном
распределении на входе распределение на выходе также равно-
мерно.
Среднюю взаимную информацию находим по формуле
(2.3.3)
88
11
(/)
(;) ()( / )log
()
kj
jkj
jk
k
py x
IXY px py x
py
==
=
=
∑∑

39
11 21
111 21
12
(/) (/)
( ) ( / ) log ( / )log ...
() ()
[
py x py x
px py x py x
py py
+++
[] []
81
81 2 8
8
(/)
( / )log ( ) ... ( ) .
()
]
py x
py x px px
py
+⋅++⋅
Выражения в квадратных скобках
[
]
⋅
численно равны, по-
этому
[
]
[
]
[
]
12 8
( ; ) ( ) ( ) ... ( )IXY px px px
=
⋅+++=⋅=
112 1 114
log 7 log 0,5963 áèò.
218 14 18
+⋅ =
2.4 Информационные характеристики случайных
последовательностей
Энтропия. Пусть имеется отрезок случайной функции X(t),
дискретной по времени и амплитуде, и он полностью определя-
ется последовательностью отсчетов
(1) ( )
,...,
n
XX, взятых в мо-
менты времени
1
,...,
n
tt. Тогда энтропия отрезка этой случайной
функции длиною в n отсчетов (m-ичных символов) равна
()
() ( )
()
() ( )
()
11
11
,, log ,, .
n
mm
nn
jk jk
jk
HXt
px x px x
==
=
−
∑∑
KK K
(2.4.1)
Для стационарных случайных последовательностей исполь-
зуют более удобную характеристику, называемую энтропией
случайной последовательности
()
()
áèò
lim .
ñè ì â
n
n
HXt
HXt
n
→∞
=
(2.4.2)
Эта величина имеет смысл средней энтропии, приходящей-
ся на один отсчёт (символ) в реализациях бесконечно большой
длины.
Энтропия случайной последовательности удовлетворяет
неравенствам (2.4.3) и (2.4.4).
+
=
=
40
(
)
(
)
1
,HXt H Xt
≤
(2.4.3)
где
(
)
1
HXt
– энтропия одного из отсчетов.
Энтропия случайной последовательности достигает наи-
большего значения (знак равенства в (2.4.3)) только тогда, когда
отдельные отсчеты функции X(t) (т.е. случайные величины
(1) ( )
,...,
n
XX) статистически независимы (см. формулу (2.2.4)).
(
)
11max
,HXt H
≤
(2.4.4)
где
1max
H – максимальное значение энтропии одного символа.
Энтропия случайной последовательности максимальна, когда
все возможные значения символов равновероятны (см. формулу
(2.2.3)). В итоге получаем
(
)
log .HXt m
≤
(2.4.5)
Можно найти и среднюю условную энтропию стационар-
ной случайной последовательности X(t). Она вычисляется при
условии, что известно значение другой дискретной случайной
последовательности Y(t), также стационарной и стационарно
связанной с X(t):
() ()
(
)
(
)
áèò
lim ,
ñè ì â
n
n
HXtYt
HXtYt
n
→∞
=
(2.4.6)
где
(
)
(
)
() () () ()
()
11
1111
... , , , , ,
n
mmmm
nn
jkr q
jkrq
HXtYt
px x y y
====
=
−
⋅
∑∑∑∑
KKK
(2.4.7)
() ( ) () ( )
(
)
11
log , , , , ,
nn
jkr q
p
xx
yy
KK
.
Взаимная информация. Среднее количество информации,
содержащейся в отрезке последовательности Y(t) относительно
отрезка X(t), равно
(
)
(
)
(
)
(
)
(
)
;,
nnn
I
Xt Yt H Xt H Xt Yt=−
а средняя информация, приходящаяся на один отсчет (символ)
.
