Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

10.19 Exercises 809

using the resultant like in Examples 10.9.1. Compare your answer with what you

would get by simple elimination of t in the equations:

Section 10.10

10.10.1. List the following monomials in three variables X

, X

, and X

in the degrevlex order:

10.10.2. Show that the degrevlex and deglex order are the same in the case of two variables.

10.10.3. Apply Algorithm 10.10.2 to the polynomials

(a) f = X

+ 2XY

- XY, p

= 3X + Y - 1

(b) f = X

Y + 1, p

= X

+ X, p

= XY + X

Use the deglex order and assume that Y < X.

10.10.4. If g(X

,...,X

) Œ k[X

,...,X

] and a

, a

,..., a

Œ k, show that

for h

,...,X

) Œ k[X

,...,X

10.10.5. Let

Find a P-normal form for f with respect to the deglex order assuming that Y < X.

10.10.6. Consider the polynomials

Let P = {p

}. Show that

with respect to the deglex order assuming that Y < X. Since f = Yp

+ p

belongs to

the ideal <P> in R[X,Y], this shows that the mere fact that a polynomial belongs to

the ideal <P> does not guarantee that every one of its P-normal forms is zero.

10.10.7. Use Theorem 10.10.12 to determine which of the following sets of polynomials P are

Gröbner bases for the ideal I, if any, with respect to the deglex order assuming that

Y < X:

(a) P = { p

= XY - Y, p

= Y

- X }

(b) P = { p

= X

+ X, p

= XY + Y, p

= Y

+ Y }

fXX

æÆææÆæ-0

and f

fXY Xp XYYp Y X XY=- =- =-Œ

[]

,, ,.R

fXYXYYY

P pXXpXXYpXYY

=+ ++

==+ =+ =-

{}

3222

,, .

gXXX hXXXX g

ni ni n

12 1 2 1 1 2

,..., , ,..., , ,...,

()

aaaa

X XXX XX XX X X

123

, ,,,,.

810 10 Algebraic Geometry

10.10.8. Use the deglex order on k[X,Y] and Algorithm 10.10.13 to ﬁnd Gröbner bases for the

ideals <P> below assuming that Y < X:

(a) P = { XY + X, X

+ Y }

(b) P = { X

Y + X, X + Y }

10.10.9. Consider the ideal I =<X

Y - X - Y,XY

+ Y> in k[X,Y]. Use a Gröbner basis to deter-

mine which, if any, of the polynomials below belongs to I. If it does, then express the

polynomial in terms of that Gröbner basis.

(a) f = X

Y + 2X

+ XY

- X

- XY

(b) f = X

Y + X

- XY + X

Y - XY

- X

10.10.10. Solve Exercise 10.9.1 using Gröbner bases.

Section 10.12

10.12.1. Let C be a plane curve in P

(k). Show that a parameterization of C deﬁned in one

coordinate system will remain a parameterization when transformed to another coor-

dinate system.

10.12.2. Show that

is a parameterization of the projective curve in P

Find its center.

10.12.3. Let g(t) be the parameterization in Exercise 10.12.2. Let h(t) = t + t

. Show by direct

computation that g

(t) =g(h(t)) has the same center as g(t).

10.12.4. Consider the irreducible curves below:

(a) Y

- X

= 0

(b) X

+ X

- Y

= 0

(One way to see that this curve is irreducible is to note that it has a parameterization

What are their singular points? Find a sequence of quadratic transformations that

transform them into curves with only ordinary singularities.

Section 10.13

10.13.1. Consider the afﬁne conic deﬁned by

f X Y X XY Y X Y,.

()

=- +-++=56 514250

g t

()

4 9 36 0

22 2

XY Z+- =.

g t

()

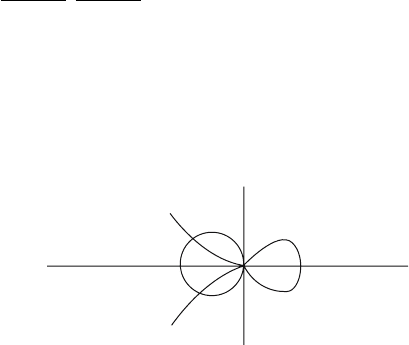
10.19 Exercises 811

Find a parameterization of the curve using the method described in Example 10.13.1

and the point (3/2,1/2) on the curve.

10.13.2. Prove Theorem 10.13.2(2).

10.13.3. (a) If f Œ k[V] is a polynomial function on an afﬁne variety V, then f: V Æ k is a con-

tinuous function with respect to the Zariski topology.

(b) Generalize (a) and prove that any polynomial function between afﬁne varieties

is continuous.

10.13.4. Prove or disprove that the following maps deﬁne isomorphisms:

(a) f:V(XY - 1) Æ R, f(x,y) = x

(b) g : R Æ V (Y

- X

), g(t) = (t

)

), h(t) = (t,t

)

10.13.5. Let X and Y be varieties in k

. Let D = { (v,v) | v Œ k

} be the diagonal in k

¥ k

(a) Show that X ¥ Y and D are varieties in k

(b) Deﬁne

Show that j deﬁnes an isomorphism between X « Y and (X ¥ Y) « D. In other

words, one can replace an intersection between varieties with the intersection

of another variety and a linear variety.

10.13.6. Show that a rational function u : V Æ W between varieties V and W is dominant if

and only if W is the smallest variety in W containing u(V).

10.13.7. Let f(X,Y) = X

- X

+ Y

and g(X,Y) = X

+ Y

+ X. Show that the map

sends the variety V(f) to the variety V(g). Show also that the two places of f with

center 0 are mapped to places of g with distinct centers. See Figure 10.22.

j XY

()

2222

jj:,.XY v vv«Æ

()

kby

Figure 10.22. The curves in Exercise

10.13.7.

+ Y

+ X = 0

– X

+ Y

= 0

812 10 Algebraic Geometry

10.13.8. Show that the map f in Example 10.13.31 cannot be expressed as a pair of homoge-

neous polynomials without common zeros.

Section 10.15

10.15.1. What is the genus of the cubic f(X,Y) = X

- Y

APPENDIX A

Notation

N = the natural numbers {0,1,2, . . .}

Z = the ring of integers

Q = the ﬁeld of rational numbers

R = the ﬁeld of real numbers

R* = the extended real numbers, that is, R » {•}

I = the unit interval [0,1]

C = the ﬁeld of complex numbers

H = the noncommutative division ring of quaternions

In the context of an n-tuple p, p

will always refer to the ith component of p. The same

holds for functions. If f:R

Æ R

, then f

is the ith component function of f, that is,

= {z = (z

,...,z

) | z

Œ N}

= {z = (z

,...,z

) | z

Œ Z}

= {p = (p

,...,p

) | p

Œ R}

= n-dimensional Euclidean space

= {p Œ R

| p

≥ 0}

= the upper halfplane of R

= {p Œ R

| p

£ 0}

= the lower halfplane of R

= {p = (p

,...,p

) | 0 £ p

£ 1}

= the unit “cube” in R

= Kronecker delta (1, if i = j, and 0, otherwise)

, e

,..., e

= standard (orthonormal) basis of R

, that is, e

= (d

,...,d

)

|v| = length of vector v

pq = the segment from point p to point q in R

, unless p and q are

quaternions, in which case this denotes their product

||pq|| = signed distance from p to q

–(u,v) = angle between vectors u and v

fff f

ppp p

()

() () ()()

, ,..., .

–

(u,v) = signed angle between vectors u and v

(p,r) = {q Œ R

| |pq| < r}

(r) = B

(0,r)

= B

(0,1)

= the open (n-dimensional) unit disk in R

(p,r) = {q Œ R

| |pq| £ r}

= an n-dimensional closed disk

= D

(0,1)

= the closed (n-dimensional) unit disk in R

n-1

= {q Œ R

| |q| = 1}

= the (n - 1)-dimensional unit sphere in R

n-1

= S

n-1

« R

= the upper hemisphere

n-1

= S

n-1

« R

= the lower hemisphere

= n-dimensional projective space

(k) = n-dimensional projective space over a ﬁeld k

[L] = [a,b,c], where L is a line in P

deﬁned, in homogeneous coor-

dinates, by the equation

There are natural inclusions: 0 = R

Ã R

Ã ...

Similarly for the other spaces above.

The map f: S

Æ S

, f(p) = -p, is called the antipodal map of S

and p and -p are

called antipodal points.

= the k-fold Cartesian product of the set X

X D Y = (X - Y) » (Y - X) (symmetric difference)

inf X = inﬁmum or greatest lower bound of the set X of real numbers

sup X = supremum or least upper bound of the set X of real numbers

cl(X) = closure of X

int(X) = interior of X

aff(X) = afﬁne hull of X

conv(X) = convex hull of X

f(a

) = right-handed limit of f at a

f(a

) = left-handed limit of f at a

(d)

(x) = the dth derivative of f

I = I

= n ¥ n identity matrix that consists of 1s along the diagonal and

0s elsewhere

the value c in the ijth position, and 0s elsewhere (if i = j, then

the ith element on the diagonal is c, not 1)

D(c

,...,c

) = n ¥ n diagonal matrix whose ith diagonal entry is c

and which

has 0s elsewhere

= transpose of the matrix A

det(A) = determinant of matrix A

tr(A) = trace of matrix A

XX X¥ ¥◊◊◊¥

1244 344

aX bY cZ++=0.

814 Appendix A Notation

= the column vector form (n ¥ 1 matrix) of the row vector v (1

¥ n matrix)

GL(n,k) = the linear group of nonsingular n ¥ n matrices over k = R or

O(n) = the group of real orthogonal n ¥ n matrices

SO(n) = the group of real special orthogonal n ¥ n matrices

ker h = kernel of a homomorphism

im h = image of a homomorphism

V(f) = set of zeroes of f (see pages 468, 675, and 676)

<a,b, . . .>=ideal generated by elements a, b, . . . in a ring

= the radical of an ideal I

R(f,g) = R

(f,g) = the resultant of polynomials f(X) and g(X)

k[V] = ring of polynomial function on V

k(V) = ﬁeld of rational functions on V

(K) = transcendence degree of ﬁeld K over k

= the complex conjugate of the complex number z

= the identity map on the set X

= the characteristic function of a set A as a subset of a given

larger set X

-1

(y) = {x | f(x) = y}

a | b = a divides b

Sign(x) =+1 if x ≥ 0 and -1 otherwise (returns an integer)

Sign(s) = sign of permutation s

=+1 if s is an even permutation, -1 if s is an odd permutation

atan2(y,x) = undeﬁned, if x = y = 0,

p/2, if x = 0 and y > 0,

-p/2, if x = 0 and y < 0,

0, if y = 0 and x > 0,

p, if y = 0 and x < 0, and

q, where -p<q<p, tan q=y/x, and q lies in the same

quadrant

as (x,y).

Note: atan2(y,x) is closely related to the ordinary arctangent tan

-1

(y/x). However,

the ordinary arctangent, which is a function of one variable, is not able

to keep track of the quadrant in which (x,y) lies, whereas atan2 does. For

example,

exp(x) = e

L(V,W) = vector space of linear (see page 873)

,...,V

;W) = Vector space of multilinear maps (see page 875)

= tangent bundle of manifold M

= normal bundle of manifold M

atan but atan233

233

()

=,, ,.

Appendix A Notation 815

Vect (M) = vector space of vector ﬁelds on the manifold M

(s) = signal curvature function of curve in R

k(s) = curvature function

t(s) = torsion function

<s>=simplicial complex generated by simplex s

[s] = oriented simplex s

(K) = group of q-chains

(K) = group of q-boundaries

(K) = group of q-cycles

(K) = q-th homology group

ª=homeomorphic, isomorphic

 = homotopic, homologous



= homotopic relative to A

Partial derivative notation for a function f:

T(A,B,...) = (A¢,B¢, . . .) : This means that T(A) = A¢, T(B) = B¢,...

Commutative diagram: In general, if one has a directed graph where the nodes are

sets and the arrows correspond to maps between these sets, then this is said to con-

stitute a commutative diagram if, whenever two directed paths start and end at the

same points, the corresponding composition of maps is equal. Commutative diagrams

are nice to have and the terminology is useful in many areas of mathematics. As an

example, consider the diagram

If G(g(a)) = F(f(a)) for all a Œ A, then the diagram is said to be commutative.

æÆæ

ØØ

æÆæ

∂

∂∂

or f f for D f D f

or f f for D f D f respectively etc

xx yy

,, ,,

,,,, ,.

11 1 2

respectively, etc,

816 Appendix A Notation

APPENDIX B

Basic Algebra

B.1 Number Theoretic Basics

Deﬁnition. If a and b, b π 0, are integers and if a = kb for some integer k, then we

say that b divides a and that b is a divisor of a. We write b|a.

Deﬁnition. A positive integer p greater than 1 whose only integer divisors are ±1 or

±p is called a prime number. Two integers a and b are said to be relatively prime if ±1

are the only common divisors. Given nonzero integers n

, n

,..., n

, the greatest

common divisor of these integers, denoted by gcd(n

,...,n

) or simply (n

) if k

= 2, is the largest integer that divides all the n

. The least common multiple of these

integers, denoted by lcm(n

,...,n

), is deﬁned to be the smallest nonnegative

integer m so that n

divides m for all i.

B.1.1. Theorem. If a and b are integers that have a greatest common divisor d, then

there are integers s and t such that

Proof. This follows from the Euclidean algorithm for integers. See, for example,

[Mill58].

Deﬁnition. Let m be an integer. Two integers a and b are said to congruent modulo

m, or mod m, if m divides a - b, equivalently, a = b + km for some k. In that case we

shall write

Deﬁnition. Let a and m be integers. If (a,m) = 1, then a is called a quadratic residue

modulo m if the congruence

has a solution; otherwise, a is called a quadratic nonresidue modulo m.

∫

()

a mod m

a b mod m .∫

()

sa tb d+=.

B.2 Set Theoretic Basics

Deﬁnition. A (binary) relation between sets X and Y is a subset S of the Cartesian

product X ¥ Y. If X = Y, then we call S a relation on X. The notation xSy is often used

to denote the fact that (x,y) Œ S.

Deﬁnition. Let S be a relation between sets X and Y. Deﬁne subsets dom(S) and

range(S), called the domain and range of S, respectively, by

and

The relation S is said to be one-to-one if x

Sy and x

Sy imply that x

= x

. The rela-

tion S is said to be onto Y if for all y in Y there is an x in X so that xSy. S is said to

be well deﬁned if xSy

and xSy

imply that y

= y

Deﬁnition. Let S be a relation on a set X. Below are names and deﬁnitions of some

common properties such a relation may possess:

Reﬂexive: For all x Œ X, xSx

Symmetric: For all x, y Œ X, if xSy, then ySx

Antisymmetric: For all x, y Œ X, if xSy and ySx, then x = y

Transitive: For all x, y, z Œ X, if xSy and ySz, then xSz

Deﬁnition. An equivalence relation on a set X is a reﬂexive, symmetric, and transi-

tive relation on X.

B.2.1. Example. It is easy to show that the congruence relation ∫ on the set of inte-

gers is an equivalence relation.

The reason that equivalence relations play such an important role in mathemat-

ics is that they capture a fundamental concept.

B.2.2. Theorem. Let X be a nonempty set.

(1) Given a relation S on X and x Œ X, deﬁne

If S is an equivalence relation, then each S

is nonempty and X is the disjoint

union of these sets.

(2) Conversely, assume that X is the disjoint union of nonempty sets A

. Deﬁne a

relation S on X by the condition that (x,y) Œ S if and only if both x and y

belong to A

for some a. Then S is an equivalence relation.

SXS

yxy=Œ

{}

range y x y for some x inSS X

()

{}

dom x x y for some y inSS Y

()

{}

818 Appendix B Basic Algebra