Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

Deﬁnition. Let L be an oriented line and let u be the unit vector that deﬁnes the

orientation of L. Let p and q be two points on L. The oriented or signed distance from

p to q, denoted by ||pq||, is deﬁned by

It is easy to check that if p π q, then ||pq|| is just the ordinary (unsigned) distance

|pq| if the vector pq induces the same orientation on L as u and -|pq| otherwise

(Exercise 1.6.6).

The angle between two vectors as deﬁned in Section 1.3 is always a nonnegative

quantity, but sometimes it is convenient to talk about a signed angle, where the sign

of the angle is determined by the direction (counterclockwise or clockwise) that the

angle “sweeps” out.

Deﬁnition. Let u and v be two linearly independent vectors in the plane R

. If q is

the angle between u and v, deﬁne –

(u,v), the signed angle between u and v, by

This ﬁnishes our discussion of the local theory of orientation. We shall return to

the subject of orientation in Chapters 6 and 8 and deﬁne what is meant by an orien-

tation at a point of a “curved” space. We shall also consider global aspects of orien-

tation and what it might mean to say that an entire space is oriented. However, in

order not to leave the reader in a kind of limbo with respect to how the deﬁnitions of

this section ﬁt into the whole picture, it is useful to give a brief sketch of what is to

come. Surfaces will serve as a good example.

Suppose that S is a smooth surface. What we mean by that is that S has a nice

tangent plane T

at every point p that varies continuously as we move from point to

point. Let us call the point where the tangent plane touches the surface its “origin.”

Since every tangent plane T

is a two-dimensional vector space, we already know what

it would mean to have an orientation s

for each T

separately. The family of orien-

tations O = {s

} is called an orientation for S if the orientations s

vary continuously

from point to point. To explain what is meant by the notion of a continuously varying

orientation, note that there is a well-deﬁned one-to-one projection p

of a neighbor-

hood of the origin in T

onto a neighborhood of p in the surface. Figure 1.14 shows

–

()

uv uv R,, ,

if the ordered basis induces the standard orientation of

otherwise.

pq pq u=∑.

1.6 Orientation 29

y = π

–1

(x)

Figure 1.14. Deﬁning continuously varying

orientations.

this correspondence in the case of a curve. This means that if two points p and q are

close, then the map

is a well-deﬁned bijection between a neighborhood of the origin in T

and a neigh-

borhood of the origin in T

. We can use this map to set up a correspondence between

ordered bases in the two tangent spaces. In this way we can compare orientations,

and we say that the orientations in O vary continuously if for nearby points s

and

correspond under p

p,q

. An oriented surface is a pair (S,O), where S is a surface and

O an orientation for S.

1.7 Convex Sets

Deﬁnition. A subset X of R

is said to be convex if, for every pair of points p and q

in X, the segment [p,q] is entirely contained in X.

Examples of convex and nonconvex sets are shown in Figure 1.15(a) and (b),

respectively. The next proposition lists some basic facts about convex sets.

1.7.1. Proposition.

(1) Both the empty set and R

are convex.

(2) Each halfplane in R

is convex.

(3) The intersection of an arbitrary number of convex sets is convex.

Proof. Part (1) is trivial and parts (2) and (3) are left as exercises for the reader

(Exercise 1.7.1 and 1.7.2).

Because convex sets have many nice properties, it is convenient to introduce the

notion of the smallest convex set that contains a set.

ppp

p,q q p

-1

30 1 Linear Algebra Topics

convex set non–convex

set

convex hull

of (b)

(a) (b) (c)

Figure 1.15. Convex and nonconvex sets and a convex hull.

Deﬁnition. Let X Õ R

. The convex hull or convex closure of X, denoted by conv(X),

is deﬁned by

This deﬁnition is similar to the one for the afﬁne hull of a set. Two facts justify it.

First, since each R

is convex, we are never taking an empty intersection. Second, by

Lemma 1.7.1(3) convex hulls are actually convex. One can also easily see that conv(X)

is contained in any convex set that contains X, which is why one refers to it as the

“smallest” such set.

1.7.2. Proposition. If X is a convex subset of R

, then conv(X) = X.

Proof. Exercise 1.7.3.

Deﬁnition. A bounded subset of R

that is the intersection of a ﬁnite number of half-

planes is called a convex linear polyhedron.

The term “bounded” means that the set is contained in some closed disk about

the origin. See Section 4.2. For example, we do not want to call R

itself a convex

linear polyhedron. A convex linear polyhedron is a special case of a linear polyhedron

that will be deﬁned in Section 6.3. It seems natural to give the deﬁnition here in order

to show that the intersection of halfplanes produces many interesting and quite

general sets and at the same time proves that these sets are convex. See Figure 1.16.

Certain convex linear polyhedra are especially interesting.

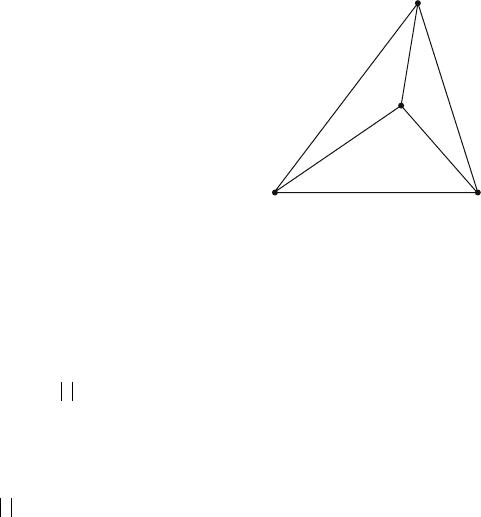
Deﬁnition. Let k ≥ 0. A k-dimensional simplex, or k-simplex, is the convex hull s of

k + 1 linearly independent points v

, v

,..., andv

in R

. We write s = v

···v

. The

points v

are called the vertices of s. Often one writes s

to emphasize the dimension

of s. If the dimension of s is unimportant, then s will be called simply a simplex. If

, w

,..., w

} Õ {v

, v

,..., v

}, then t = w

···w

is called a j-dimensional face

of s and we shall write t Ɱ s.

Figure 1.17 shows some examples of simplices and shows that our use of the term

“k-dimensional” is justiﬁed. Note that R

does not contain any three-dimensional

conv XCC X

()

=«

{}

is a convex set that contains .

1.7 Convex Sets 31

Figure 1.16. A convex linear polyhedron X.

simplex. In general, R

contains at most n-dimensional simplices because it is not

possible to ﬁnd j linearly independent points in R

for j > n + 1. Also, a simplex depends

only on the set of vertices and not on their ordering. For example, v

= v

. K-

simplices are the simplest kind of building blocks for linear spaces called simplicial

complexes, which are deﬁned in Chapter 6, and they play an important role in alge-

braic topology. They have technical advantages over other regularly shaped regions

such as cubes. In particular, their points have a nice representation as we shall show

shortly in Theorem 1.7.4.

1.7.3. Lemma.

(1) The set aff({v

,...,v

}) consists of the points w that can be written in the

form

(1.25)

(2) The set conv({v

,...,v

}) consists of the points w that can be written in the

form

Proof. To prove (1), let

Sv==

ÂÂ

ii i

wv=Œ

[]

ÂÂ

a where a and a

ii i i

,, .01 1

wv==

ÂÂ

a where a

ii i

,.1

32 1 Linear Algebra Topics

(a)

s = v

(b)

= v

is the

line segment

from v

to v

(c)

= v

is the

solid triangle

(d)

= v

the solid tetrahedron

Figure 1.17. Some simplices.

If w belongs to aff({v

,...,v

}), then we know from Theorem 1.4.4 that

This equation can be rewritten in the form

which shows that w belongs to S. Conversely, if w belongs to S, then

This equation can be rewritten in the form

Part (1) is proved.

To prove (2), let

We need to show that S is the smallest convex set containing {v

,...,v

}. We show

that S is convex ﬁrst. Consider two points

in S and let t Œ [0,1]. Then

Clearly, 0 £ ta

+ (1 - t)b

. Furthermore,

ta tb t a t b

()()

()

=◊+ -

()

◊

===

ÂÂÂ

11 1

000

pw w v v

=+-

()

¢=

()

=+-

()()

ÂÂ

ttta tb

ta tb

iii

wv w v=¢=

ÂÂ

a and b

Sv=Œ

[]

ÂÂ

a a and a

ii i i

01 1

wv vv vv=+ ++

0 101 0

a a

....

wv==

ÂÂ

1for some a such that

wvvv=-- -

()

+++1

1011

ttt t

kkk

... ... ,

w v vv vv R=+ + + Œ

0 101 0

tt t

kk i

.... .for some

1.7 Convex Sets 33

This also shows that ta

+ (1 - t)b

£ 1; hence the point p belongs to S, proving that S

is convex since p is a typical point on the segment from w to w¢.

Next, we show that S belongs to every convex set C containing the points v

, v

..., andv

. The case k = 0 is trivial. Assume that k ≥ 1 and that the statement has

been proved for all values smaller than k. Let

belong to S. Since not all a

can be zero, we may assume without loss of generality

that a

π 0. The case a

= 1 is trivial, and so assume that a

< 1. Thus we can write

But

and 0 £ a

/(1 - a

) £ 1. By our inductive hypothesis

belongs to every convex set containing v

, v

,..., andv

. In particular, u belongs to

C. Since v

belongs to C, it follows that w = a

+ (1 - a

)u belongs to C and we are

done. Therefore,

and (2) is proved.

An interesting consequence of Lemma 1.7.3(1) is that it gives us a homogeneous

way of deﬁning a plane. We could deﬁne a k-dimensional plane as a set deﬁned by k

+ 1 linearly independent points v

, v

,..., v

which satisfy equation (1.25) instead of

the deﬁnition we gave in Section 1.5 that involved a point and a basis.

Lemma 1.7.3(2) motivates the following deﬁnition.

Deﬁnition. An expression of the form

a where a and a

ÂÂ

[]

01 1,, ,

Svvv=

{}

()

conv

, ,...,

uv=

()

ÂÂ

wv v=+-

()

00 0

wv=

34 1 Linear Algebra Topics

and where the v

are any objects for which the expression makes sense is called a

convex combination of the v

1.7.4. Theorem. Let v

, v

,..., v

be k + 1 linearly independent points.

(1) Every point w of aff({v

,...,v

}) can be written uniquely in the form

(2) Every point w of the simplex s = v

···v

can be written uniquely in the

form

Furthermore, the dimension and the vertices of a simplex are uniquely deter-

mined, that is, if v

···v

= v

¢v

...

¢, then k = t and v

= v

¢ after a renum-

bering of the v

¢.

Proof. Lemma 1.7.3 showed that every point w has a representation as shown in (1)

and (2). We need to show that it is unique. Suppose that we have two representations

of the form

Then

The second to last equality sign follows from the fact that

0ww v v

vv v

=-= -

()

ÂÂ

aa aa

ii ii

iii

()

wv v==

ÂÂ

ii ii

wv=Œ

[]

ÂÂ

a where a and a

ii i i

,,,.01 1

wv==

ÂÂ

a where a

1,.

1.7 Convex Sets 35

But the vectors v

- v

, v

- v

,..., and v

- v

are linearly independent, so that

= a

¢ for i = 1,2, . . . ,k, which then also implies that a

= a

¢. This proves that the rep-

resentation for w is unique.

The rest of part (2) is left as an exercise.

Deﬁnition. Using the notation in Theorem 1.7.4(1), the a

are called the barycentric

coordinates of w with respect to the points v

. The point

is called the barycenter of the simplex s.

1.7.5. Example. Let v

= (1,0), v

= (4,0), and v

= (3,5). We want to ﬁnd the barycen-

tric coordinates (a

) of w = (3,1) with respect to these vertices.

Solution. We must solve

for a

, a

, and a

. Since a

= 1 - a

- a

, we really have to solve only two equations in

two unknowns. The unique solutions are a

= 4/15, a

= 8/15, and a

= 1/5. The barycen-

ter of the simplex v

is the point (8/3,5/3).

Theorem 1.7.4 shows that barycentric coordinates are another way to parame-

terize points, which is why that terminology is used. They are a kind of weighted sum

and are very useful in problems that deal with convex sets. In barycentric coordinates,

the point w in the deﬁnition would be represented by the tuple (a

,...,a

). The

barycenter would have the representation

Barycentric coordinates give information about ratios of volumes (or areas in

dimension 2). (For a general deﬁnition of volume in higher dimensions see Chapter

4.) Consider a simplex s = v

···v

and a point w in it. Let (a

,...,a

) be the

barycentric coordinates of w. Let D be the volume of s and let D

be the volume of the

simplex with vertices v

, v

,..., v

i-1

, w, v

i+1

,..., v

. See Figure 1.18.

1.7.6. Proposition.

Proof. See [BoeP94].

Finally, barycentric coordinates are useful in describing linear maps between sim-

plices. Let f be a map from the set of vertices of a simplex s onto the set of vertices

1kk k++ +

, ,..., .

aaa

01 2

10 40 35 31,,,,

()

+++

()

vv v...

aa a a

()

=-=

===

ÂÂÂ

000

11 0.

36 1 Linear Algebra Topics

of another simplex t. Let s = v

···v

and t = w

···w

. If we express points of s

in terms of the (unique) barycentric coordinates with respect to its vertices, then f

induces a well-deﬁned map

deﬁned by

Deﬁnition. The map |f| is called the map from s to t induced by the vertex map f.

In Chapter 6 we shall see that the map f is a special case of what is called a sim-

plicial map between simplicial complexes and |f| is the induced map on their under-

lying spaces. The main point to note here is that a map f of vertices induces a map

|f| on the whole simplex. (This is very similar to the way a map of basis vectors in a

vector space induces a well-deﬁned linear transformation of the whole vector space.)

This gives us a simple abstract way to deﬁne linear maps between simplices, although

a formula for this map in Cartesian coordinates is not that simple. See Exercises 1.7.6

and 1.7.7.

1.8 Principal Axes Theorems

The goal of this section is to state conditions under which a linear transformation can

be diagonalized. We shall be dealing with vector spaces over either the reals or the

complex numbers. We refer to the main theorems of this section as “principal axes

theorems” because they can be interpreted as asserting the existence of certain coor-

dinate systems (coordinate axes) with respect to which the transformation has a par-

ticularly simple description. Such diagonalization theorems are special cases of what

are usually called “spectral theorems” in the literature because they deal with the

eigenvalues (the “spectrum”) of the transformation.

fa af

ÂÂ

()

f:stÆ

1.8 Principal Axes Theorems 37

Figure 1.18. Barycentric coordinates and volume ratios.

In the ﬁnal analysis, it will turn out that a transformation is diagonalizable if the

matrix associated with it is symmetric or Hermitian. Unfortunately, those properties

of a matrix are not independent of the basis that is used to deﬁne the matrix. For

example, it is possible to ﬁnd a transformation and two bases, so that the matrix is

symmetric with respect to one basis and not symmetric with respect to the other. The

deﬁnition that captures the essence of the symmetry that we need is that of the

“adjoint” transformation.

1.8.1. Lemma. Let V be an n-dimensional vector space over a ﬁeld k. If a:V Æ k is

a nonzero linear functional, then

Proof. Since a is nonzero, dim im(a) = 1 and so the lemma is an immediate conse-

quence of Theorem B.10.3.

If the vector space V has an inner product •, then it is easy to check that for each

u Œ V the map

deﬁned by

is a linear transformation, that is, a linear functional. There is a converse.

1.8.2. Theorem. If a is a linear functional on an n-dimensional vector space V with

inner product •, then there is a unique u in V, so that

for all v in V.

Proof. If a is the zero map, then u is clearly the zero vector. Assume that a is

nonzero. Then by Lemma 1.8.1, the subspace X = ker(a) has dimension n - 1. Let u

be any unit vector in the one-dimensional orthogonal complement X

of X. We show

that

is the vector we are looking for. (The complex conjugate operation is needed in case

we are dealing with vector spaces over the complex numbers.) If v is an arbitrary

vector in V, then V = X ≈ X

implies that v = x + cu, for some x in X and some scalar

c. But

uuu=

()

a vuv

()

=∑

u* vvu

()

=∑

uk*: V Æ

dim ker a

()

=-n1.

38 1 Linear Algebra Topics