Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

A necessary condition is clearly that f

(Z,z

)) Õ p

(Y,y

)). The amazing fact is

that this condition is also sufﬁcient provided that some weak connectivity conditions

hold.

Deﬁnition. A topological space X is said to be locally path-connected if every neigh-

borhood of a point contains a neighborhood that is path-connected.

Fortunately, the spaces of interest to us are locally path-connected. Manifolds are

trivially locally path-connected, but so are CW complexes (use induction on the

number of cells).

7.4.2.11. Theorem. Let (Y,p) be a covering space for a space X. Let Z be a path-

connected and locally path-connected space. Let x

Œ X, y

Œ p

-1

), and z

Œ Z. Then

a map f : (Z,z

) Æ (X,x

) lifts to a map f

: (Z,z

) Æ (Y,y

) if and only if f

(Z,z

)) Õ

(Y,y

)).

Proof. See [Mass67] or [Jäni84]. The diagram below should help clarify what is

being said:

We can deduce a number of important results from Theorem 7.4.2.11.

7.4.2.12. Theorem. Let (Y

) and (Y

) be covering spaces for a space X, where

and Y

are path-connected and locally path-connected spaces. Let x

Œ X and y

-1

). The two covering spaces are isomorphic via a bundle isomorphism f : (Y

)

Æ (Y

) if and only if p

)) = p

)).

Proof. See [Mass67]. The following diagram might again help:

To get the next theorem we need another technical deﬁnition.

122

2122

()

()()

æÆæ

()

p ,

111

1111

()

()()

ppp

10 10 1 0

Zz Zz Xx,,,.

()

æÆæ

()()

()

Yy Yy

Zz Xx Yy

,, ,

010

0010

()

ØØ

æÆæ

()()

fp p

Zz Xx

æÆæ

7.4 Homotopy Theory 429

Deﬁnition. A topological space X is said to be semi-locally simply connected if every

point x in X has a neighborhood U so that every closed curve in U that starts at x is

homotopic to a constant map in X.

Manifolds and CW complexes are semi-locally simply connected (use induction

on the number of cells for CW complexes).

7.4.2.13. Theorem. Let X be a path-connected, locally path-connected, and semi-

locally simply connected space. Let x

Œ X. If G is an arbitrary subgroup of p

(X,x

then there is a path-connected and locally path-connected space Y and covering space

(Y,p) of X, so that for some point y

Œ p

-1

), p

(Y,y

)) = G.

Proof. See [Mass67] or [Jäni84].

Deﬁnition. A universal cover or universal covering space for a space X is a covering

space (Y,p) for X, with the property that Y is path-connected, locally path-connected,

and simply connected.

By Theorem 7.4.2.12, the universal covering space of a space (if it exists) is unique

up to isomorphism. Therefore, if the projection p is obvious from the context, then

the common expression “the universal cover Y of X” refers to the universal covering

space (Y,p).

7.4.2.14. Example. The space R is the universal cover of the circle S

(see Example

7.4.2.2).

7.4.2.15. Example. The sphere S

is the universal cover of projective space P

(see

Example 7.4.2.1).

7.4.2.16. Theorem. Let X be a path-connected, locally path-connected and semi-

locally simply connected space. Then X has a universal covering space and any two

are isomorphic.

Proof. Only the existence part of this theorem needs proving. See [Mass67] or

[Jäni84].

The reason that a universal covering space (Y,p) for a space X has the name it

has is that if (Y¢,p¢) is any other covering space for X, then there a unique (up to iso-

morphism) map p˜ : Y Æ Y¢ making the following diagram commutative

In fact, (Y,p˜) will be a covering space for Y¢. In other words, the universal covering

space of a space “covers” every other covering space of the space.

The covering transformations of a covering space are interesting. They obviously

form a group.

æÆæ¢

¢pp

430 7 Algebraic Topology

Deﬁnition. Cov(Y,p) will denote the group of covering transformations of a cover-

ing space (Y,p).

7.4.2.17. Theorem. Let (Y,p) be a covering space for a path-connected and locally

path-connected space X. Let x

Œ X and y

Œ p

-1

). Let G = p

(Y,y

)) and let N

be the normalizer of G in p

(X,x

). Given an element [g] Œ N

, there is exactly one

covering transformation h

[g]

that maps y

into the end point g˜(1) of the lifting g˜ of g

that starts at y

. The map

is a homomorphism with kernel G, that is,

Proof. See [Mass67] or [Jäni84].

7.4.2.18. Corollary. Let (Y,p) be the universal covering space for a path-connected

and locally path-connected space X and let x

Œ X. Then Cov(Y,p) ªp

(X,x

). If

(X,x

) is ﬁnite and n =Ωp

(X,x

)Ω, then (Y,p) is an n-fold covering.

7.4.2.19. Example. The covering transformations of the universal covering space

(R,p) deﬁned in Example 7.4.2.2 are the maps

deﬁned by

The maps h

are obviously covering transformations. Note that h

= h

7.4.2.20. Example. The only covering transformation of the covering space S

over

is the antipodal map of S

7.4.2.21. Corollary. Let (Y,p) be the universal covering space for a path-connected

and locally path-connected space X and let x

Œ X. Then X ª Y/~, where ~ is the equiv-

alence relation deﬁned by y ~ y¢ if there is an h Œ Cov(Y,p), such that y¢=h(y).

7.4.2.22. Example. Let m, n Œ Z. Deﬁne maps

hxyx my n

mn,

()

=+ +

()

22pp

mn,

: RR

ht t n

()

=+2p .

: RRÆ

Cov p

Y,.

()

N Cov p

()

[]

7.4 Homotopy Theory 431

and think of the torus S

¥ S

as the quotient space of R

/~, where ~ is the equiva-

lence relation

If p : R

Æ R

/~ is the quotient map, then (R

,p) is the universal covering space of the

torus. With this interpretation, the maps h

m,n

are obviously the covering transforma-

tions. Note that h

m,n

= h

1,0

0,1

Using Corollary 7.4.2.18 and what we showed in Examples 7.4.2.19, 7.4.2.20, and

7.4.2.22 we now have alternate proofs of the facts stated in Theorem 7.4.1.10(1) and

(2) and Corollary 7.4.1.15, namely,

7.4.2.23. Corollary.

(1) p

) ª Z.

(2) p

) ª Z

(3) p

¥ S

) ª Z ≈ Z.

All this talk about covering transformations and the last three examples leads to

another question. Suppose that we turn things around and start with a group of

homeomorphisms G of a space Y and deﬁne

(7.8)

where

Deﬁnition. The space Y/G in equation (7.8) is called the quotient space of Y modulo

the group G.

If p : Y Æ Y/G is the quotient map, then is (Y,p,Y/G) a covering space with G the

group of covering transformations? The answer in general is no. At the very least the

homeomorphisms in G could not be allowed to have ﬁxed points, but we need some-

thing stronger.

Deﬁnition. A group of homeomorphism G of a space X is said to be properly

discontinuous if every point x in X has a neighborhood U so that all the sets h(U),

h Œ G, are disjoint.

Clearly, no homeomorphism in a properly discontinuous group of homeomor-

phism can have a ﬁxed point. Furthermore, it is easy to see that the covering

transformations of a covering space form a properly discontinous group of homeo-

morphisms of the total space.

7.4.2.24. Theorem. Let Y be a connected, locally path-connected topological space

and G a properly discontinuous group of homeomorphism of Y. If p : Y Æ Y/G is the

yy y y

12 2 1

~ if h for=

()

Œ some h G.

YG Y= ~,

xy h xy

,,.

() ()

432 7 Algebraic Topology

quotient map, then (Yp) is a covering space for Y/G with G the group of covering

transformations.

Proof. See [Mass67].

As a nice application of this discussion of covering transformations we relate this

to the lens spaces deﬁned in Section 7.2.4. As before, let p and q be relatively prime

positive integers and assume that 0 £ q £ p/2. Consider the unit sphere S

in complex

2-space C

. (One can identify C

with R

.) Deﬁne rotations

where z

, z

Œ C and i = 0, 1,..., p-1. (The e

2pi/p

are the pth roots of unity.) Since

, we have in effect deﬁned a group

of order p of rotations acting on S

. Deﬁne

and let

be the quotient map.

7.4.2.25. Theorem. The new spaces L(p,q) are homeomorphic to the lens spaces

L(p,q) deﬁned in Section 7.2.4. Furthermore,

(1) (S

,h) is the universal covering space for L(p,q).

(2) G = Cov(S

,h).

Proof. See [CooF67] or [HilW60]. Parts (1) and (2) are obvious.

7.4.2.26. Corollary. p

(L(p,q)) ª Z

This concludes our overview of the theory of covering spaces. The gist of the main

results stripped of their technical details is summarized by the following:

(1) The theory of covering spaces for simply connected spaces is uninteresting

because the only covering space in that case is where the space covers itself.

(2) The universal covering space of a space covers every other covering space of

the space.

h:,S

()

Lpq

Lpq G,

()

= S

{}

ss s

01 1

, ,...,

i p qi p

eezz z z

12 1

,,,

()

: SS

7.4 Homotopy Theory 433

(3) The covering transformations of the universal covering space of a space have

no ﬁxed points and are in one-to-one correspondence with the elements of the fun-

damental group of the space. They act transitively on the ﬁbers, that is, any point in

the total space can be mapped into any other point belonging to the same ﬁber as the

ﬁrst.

(4) Every conjugacy class of a subgroup of the fundamental group of a space

deﬁnes a covering space for that space.

See [Jäni84] for a variety of applications of covering space theory.

7.4.3 Higher Homotopy Groups

There is an important generalization of the fundamental group of a space that leads

to higher-dimensional homotopy groups.

Deﬁnition. Let n ≥ 2. Given maps a, b : (I

,∂I

) Æ (X,x

), deﬁne a map

Deﬁnition. Let

be the set of equivalence classes of maps a with respect to the equivalence relation



∂I

. Deﬁne a product * on p

(X,x

) as follows: If [a], [b] Œp

(X,x

), then

7.4.3.1. Theorem. The operation * on p

(X,x

) is well deﬁned and makes p

(X,x

)

into a group called the nth homotopy group of the pointed space (X,x

Proof. The proof is similar to the one for the fundamental group. Exercise 7.4.3.1.

There is a perhaps easier way to visualize the product in p

(X,x

). First, we need

a deﬁnition.

Deﬁnition. Let X, Y, and Z be pointed spaces with base points x

, y

, and z

, respec-

tively. If f : X Æ Z and g : Y Æ Z are continuous maps with f(x

) = z

and g(y

) = z

then deﬁne a map

abab

[]

paa∂

∂

Xx I I Xx

,:,,

()

{}



ab a

()( )

()

££

()

££

t t t t t t if t

tt t ift

12 12 1

12 1

, ,..., , ,..., , ,

, ,..., , .

ab ∂*

()

:, ,II Xx

434 7 Algebraic Topology

This map is called the wedge of f and g.

With this deﬁnition we can now give an alternate deﬁnition of the product in

(X,x

). First of all, we can clearly identify maps (I

,∂I

) Æ (X,x

) with maps (S

)

Æ (X,x

). Let

(7.9)

be the map that collapses S

n-1

to the base point of S

⁄ S

and that wraps the upper

and lower hemisphere of S

around the ﬁrst and second factor of S

⁄ S

, respectively.

Let [a], [b] Œp

(X,x

). If we represent a and b as maps

then the product [a]*[b] is nothing but the homotopy class of the composite map

(a⁄b)

c. See Figure 7.29.

We now have homotopy groups p

(X,x

) deﬁned for n ≥ 1. It is convenient to make

a deﬁnition for n = 0. Note that S

= {-1,+1}.

Deﬁnition. p

(X,x

) is deﬁned to be the set (there is no group structure) of homo-

topy classes of maps

(Equivalently, p

(X,x

) is the set of path components of X.)

Although p

(X,x

) has no group structure, one often refers to it as the 0th homo-

topy “group.”

7.4.3.2. Theorem. The group p

(X,x

) is abelian whenever n ≥ 2.

Proof. Figure 7.30 shows how to construct a homotopy between a*b and b*a.

Just as in the case of the fundamental group, higher homotopy groups are inde-

pendent of the base point if the space is path-connected. One therefore often writes

(X) instead of p

(X,x

f: , , .SXx

()

ab,: , , ,Se Xx

()

nnn

: SSSÆ⁄

fg byfg fandfg g⁄⁄Æ ⁄= ⁄=:.XY Z X Y

7.4 Homotopy Theory 435

n–1

⁄S

(a⁄b)

Figure 7.29. Using the wedge operation to

deﬁne a homotopy group

product.

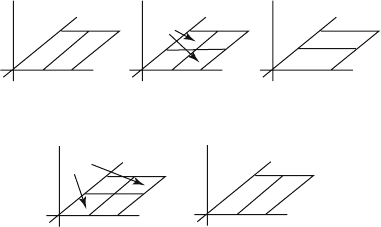
Continuous maps induce homomorphisms on the homotopy groups in a natural

way, similar to how it was done in the case of the fundamental group. Let (X,x

) and

(Y,y

) be pointed spaces. Given a continuous map

deﬁne

7.4.3.3. Lemma. The map f

is well deﬁned. It is a homomorphism of groups when

n ≥ 1.

Proof. Exercise 7.4.3.2.

Deﬁnition. The map f

is called the homomorphism induced by the continuous map

The fact that the higher (n ≥ 2) homotopy groups are abelian sets them apart from

the fundamental group. In other ways, they satisfy similar properties however. For

example, one can show, just like in Theorem 7.4.1.14, that there are isomorphisms

(By the way, no such isomorphism exists for homology. A theorem, the Künneth

theorem, relates the homology of the product of two spaces to that of the spaces but

it is much more complicated.) There are also natural homomorphisms

(7.10)

mp:, ,

HXx X

()

ppp

nnn

XYx y Xx Yy¥¥

()

,,,.

00 0 0

[]

()

[]

aao .

nn*

()

≥:, ,, ,ppXx Yy

f: , ,Xx Yy

()

436 7 Algebraic Topology

Figure 7.30. Proving the commutativity of

homotopy groups.

called the Hurewicz homomorphisms, which generalize the homomorphism for the

fundamental group. (We are again pretending that H

(X) is well deﬁned.) These

homomorphisms are neither onto nor one-to-one in general though. The homotopy

groups capture the idea of “holes” better than the homology groups. After all, the

n-sphere S

is the prototype of an n-dimensional “hole.”

Nontrivial “higher” homotopy groups of spheres are one important example of

what sets homotopy groups apart from homology groups. The homology groups H

(X)

are all 0 if i is larger than the dimension of X, but this is not necessarily the case for

homotopy groups. For example,

One well-known theorem that relates the homotopy and homology groups in a

special case is

7.4.3.4. Theorem. (The Hurewicz Isomorphism Theorem) If n ≥ 2 and if X is a con-

nected polyhedron whose ﬁrst n - 1 homotopy groups vanish, then the Hurewicz

homorphism

is an isomorphism.

Proof. See [Span66].

Theorem 7.4.3.4 is one result that can be used to compute higher homotopy

groups.

7.4.3.5. Theorem. Let n ≥ 1.

(1) p

) = 0 for 0 £ i < n.

(2) p

) ª Z.

Proof. To prove (1) consider a map f : S

Æ S

. The map f is homotopic to a map

that misses a point, say e

n+1

. (To prove this fact, use the simplicial approximation

theorem with respect to some triangulations of the spheres.) But S

- e

n+1

is home-

orphic to an open disk that is contractible. It follows that f is homotopic to a constant

map and proves (1). The case n = 1 in part (2) is just Corollary 7.4.2.23(1). If n > 1,

then (2) follows from (1), Theorem 7.4.3.4, and Theorem 7.2.3.4.

It should be noted that Theorem 7.4.3.4 implies nothing about the homomor-

phisms

for i > n (n as in the theorem). In general, homotopy groups are much harder to

compute than homology groups but they are stronger invariants than homology

groups. As an example of the latter, there is the following theorem:

mp:,

HXx X

()

mp:,

HXx X

()

ª .

7.4 Homotopy Theory 437

7.4.3.6. Theorem. A continuous map f : X Æ Y between CW complexes is a homo-

topy equivalence if and only if it induces isomorphisms on all (n ≥ 0) homotopy

groups.

Proof. See [LunW69].

The best that one can do for homology is

7.4.3.7. Theorem. Let X and Y be simply connected CW complexes. A continuous

map f : X Æ Y is a homotopy equivalence if and only it induces isomorphisms on all

homology groups.

Proof. See [Span66].

Theorem 7.4.3.7 is false if X and Y are not simply connected. For a counter-

example, see [Span66], page 420. There is an analog of the theorem when spaces are

not simply connected, but things get much more involved. It is based on the notion

of a simple homotopy equivalence. See [Dieu89].

We ﬁnish with one last application.

Deﬁnition. A topological space that has the homotopy type of the n-sphere S

called a homotopy n-sphere. A polyhedron is called a homology n-sphere if it has the

same homology groups as S

7.4.3.8. Theorem. Every simply connected homology n-sphere, n ≥ 2, is a homo-

topy n-sphere.

Proof. By Theorems 7.4.3.4 we get a map between the S

and the space that is an

isomorphism on homology. Now use Theorem 7.4.3.7.

Theorem 7.4.3.8 is also false if we drop the simply connected hypothesis. In

[SeiT80] one can ﬁnd an example of a three-dimensional space, called a Poincaré

space, that is a homology 3-sphere but that has a nontrivial fundamental group and

hence cannot be of the same homotopy type as S

(nor homeomorphic to it). The nice

thing about Theorems 7.4.3.7 and 7.4.3.8 is that, in order to prove something about

homotopy type, we do not have to mess around with complicated homotopy groups

but can simply work with homology groups, which is a much easier task. We do have

to check that spaces are simply connected though.

7.5 Pseudomanifolds

This section specializes to manifold-like spaces. We shall deﬁne what it means for

them to be orientable and relate this concept to homology. Some applications of this

can be found in the next section.

Deﬁnition. A polyhedron X is called an n-dimensional pseudomanifold or n-

pseudomanifold or simply pseudomanifold if it admits a triangulation (K,j) satisfying

438 7 Algebraic Topology