Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

Proof. The corollary follows from Theorems 7.4.1.10(1) and 7.4.1.14. See also Corol-

lary 7.4.2.23(3).

Theorem 7.4.1.10(3) showed that the fundamental group of a space is not neces-

sarily abelian. Is there any connection between it and the ﬁrst homology group? After

all, in both cases we are dealing with one-dimensional “holes.” To answer that ques-

tion we describe a natural map from one to the other.

Note. To simplify the discussion below we are pretending (as we earlier said we

would) that polyhedra have well-deﬁned homology groups.

Let X be a connected polyhedron and let x

Œ X. Deﬁne

as follows: Let [a] Œp

(X,x

), where a:(I,∂I) Æ (X,x

). If is the map

then a induces a unique map b:S

Æ X with the property that a(t) =b(j(t)). (b is the

unique map that makes the diagram

commutative.) Now b induces a map b

on homology groups. If i is a ﬁxed (“stand-

ard”) generator of H

), then

7.4.1.16. Theorem.

(1) The map m deﬁnes a homomorphism of groups called the Hurewicz

homomorphism.

(2) The map m sends p

(X,x

) onto H

(X).

(3) The kernel of m is the commutator subgroup of p

(X,x

Proof. See [Cair68].

It follows from Theorem 7.4.1.16 that H

(X) is the abelianization of p

(X,x

). The

advantage of the fundamental group of a space is that it gives somewhat more infor-

mation about the space than the ﬁrst homology group. The disadvantage is that it is

more complicated to compute.

ma b

[]

()

i H

X .

(I,∂I)

jppttt

()

cos ,sin ,22

j : ISÆ

mp:,

10 1

Xx X

()

7.4 Homotopy Theory 419

Deﬁnition. A path-connected space that has a trivial fundamental group is called

simply connected.

Analyzing spaces and maps gets much more complicated if the spaces involved

are not simply connected. The fundamental group has a subtle but signiﬁcant inﬂu-

ence on the topology of a space and its name is quite appropriate. It is probably the

single most important group from the point of view of algebraic topology. A great

many theorems have as part of their hypotheses the assumption that a space is simply

connected. See for example Theorems 7.4.3.7 and results in Section 8.7, 8.9, and 8.10.

A nice way to summarize some aspects of the fundamental group and its rela-

tionship to the ﬁrst homology group is as follows: If

is a continuous map, then (again ignoring the current nonuniqueness of homology

groups) there is a commutative diagram

where m is the Hurewicz homomorphism.

We end this section with an application of the fundamental group. The group plays

a central role in the study of knots. Some references for knot theory are [CroF65],

[Livi93], [Rolf76], and [Mass67].

Deﬁnition. A subspace K of R

is called a knot if K is homeomorphic to S

. The

space R

- K is called the complement of the knot K. Two knots K

and K

are said

to be equivalent if there is a homeomorphism h:R

Æ R

, so that h(K

) = K

.The equiv-

alence class of a knot is called its knot type. A knot is trivial if it is equivalent to the

standard S

in R

. A knot is called a polygonal knot if it is the union of a ﬁnite number

of (linear) segments, that is, it is a polygonal curve. A knot is said to be tame if it is

equivalent to a polygonal knot.

We are sticking to the traditional theory here, because the deﬁnition of a knot is

sometimes generalized to include imbeddings of n-spheres, n ≥ 1, in a space. We also

need to point out that there are other variations of the deﬁnition of a knot in the lit-

erature. Sometimes knots are deﬁned to be maps, that is, imbeddings k:S

Æ R

rather than subsets. In that case, the equivalence of knots is deﬁned in terms of

isotopies. (Two imbeddings h

and h

are said to be isotopic if there exists a one-

parameter family of imbeddings h

, or isotopy, between them.) Fortunately, there is

not much difference between the theories. For example, if we stick to orientation-

preserving homeomorphisms, then two knots are equivalent using our deﬁnition if

and only if they are isotopic. (We shall deﬁne what it means for a homeomorphism

between oriented manifolds to be orientation preserving in Section 7.5.1. A homeo-

morphism h:R

- K Æ R

- K is said to be orientation preserving if its extension to

Æ S

is.)

10 10

Xx Yy

()

æÆæ

()

ØØ

()

æÆæ

()

f: , ,Xx Yy

()

420 7 Algebraic Topology

7.4 Homotopy Theory 421

Sometimes it is convenient to consider knots in S

rather than R

because S

is a

compact space, but there is again no real difference in the theory since, using the

stereographic projections, S

can be thought of as just R

with one point added. Note

also that, since all knot, are homeomorphic to S

, classifying them is not a question

of determining if they themselves are homeomorphic because they are. What makes

knots different is their imbedding in R

. Every knot in the plane is necessarily trivial

by the Schoenﬂies theorem.

In order not to have to deal with wild imbeddings, one also usually assumes that

knots are polygonal.

Deﬁnition. Let K be a knot. The fundamental group p

- K) is called the group

of the knot K. (The base point of the fundamental group was omitted because we are

only interested in the group up to isomorphism.)

The group of a knot plays a large role in the study of knots but does not deter-

mine the knot completely because there exist inequivalent knots that have the same

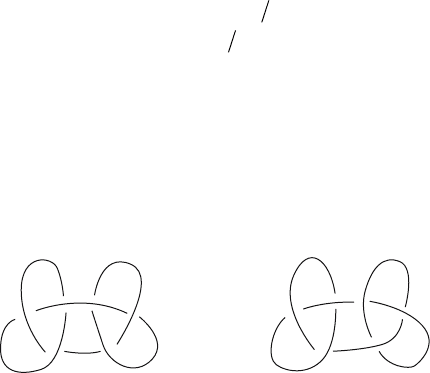
knot group, such as for example, the square knot and the granny knot shown in Figure

7.22. Certainly, equivalent knots have isomorphic knot groups because their comple-

ments are homeomorphic. The knot group is only one of many interesting invariants

associated to a knot.

Before we list a few important known facts about the classiﬁcation of knots, we

deﬁne a well-known inﬁnite family of knots that serve as useful examples.

Deﬁnition. A torus knot of type (p,q), where p and q are relatively prime, is a knot

that can be imbedded in a torus and has the property that it cuts a meridian circle of

the torus in p points and a circle of latitude in q points. In cylindrical coordinates, a

speciﬁc instance of such a knot is the curve

that lies in the torus in R

(the circle in the x-z plane with center (2,0,0) and radius

1 rotated about the z-axis) deﬁned by the equation

rz-

()

+=21

rqp

zqp

()

2 cos

sin

square knot granny knot

Figure 7.22. Two inequivalent knots with isomorphic knot groups.

422 7 Algebraic Topology

Figure 7.23 shows an example of a torus knot.

7.4.1.17. Theorem.

(1) A tame knot is trivial if and only if the group of the knot is inﬁnite cyclic (iso-

morphic to Z). There is an algorithm that determines whether or not a knot

is trivial.

(2) Two tame knots have homotopy equivalent complements if and only if their

knot groups are isomorphic. (Conjecture: If two tame knots have homeomor-

phic complements, then they have the same knot type.)

(3) There exist inﬁnitely many knot types. For example, the torus knots of type

(p,q) are all inequivalent.

(4) The abelianization of every knot group is inﬁnite cyclic.

(5) If K is a tame knot, then p

- K) = 0 for i > 1.

Proof. The proofs of most of these facts are much too complicated to give here. See

the references for knot theory listed earlier.

7.4.2 Covering Spaces

The topic of this section is intimately connected with the fundamental group but also

has important applications in other areas such as complex analysis and Riemann sur-

faces. Section 8.10 in the next chapter will continue the discussion and discuss the

related topic of vector bundles.

We begin with some basic terminology and motivational remarks. See Figure 7.24.

Deﬁnition. A bundle over a space X is a pair (Y,p), where Y is a topological space

and p:Y Æ X is a continuous surjective map. One calls Y the total space, p the pro-

jection, and X the base space of the bundle. The inverse images p

-1

(x) Õ Y for x Œ X,

are called the ﬁbers of the bundle.

In our current context we should think of the total space of a bundle as consist-

ing of a union of ﬁbers that are glued together appropriately. Of course, the general

case of an arbitrary surjective map p does not lead to anything interesting. The inter-

esting case is where all the ﬁbers are homeomorphic to a ﬁxed space F. The obvious

example of that is the product of the base space and F.

Deﬁnition. A bundle over X of the form (X ¥ F,p), where p is the projection onto

the ﬁrst factor deﬁned by p(x,f) = x, is called the product bundle with ﬁber F.

Figure 7.23. A torus knot of type (3,5).

Next, we deﬁne a notion of equivalence of bundles over a space. We begin by deﬁn-

ing general bundle maps. They should preserve the ﬁbers (map ﬁbers to ﬁbers) since

that is the only structure present.

Deﬁnition. A bundle map from a bundle (Y

) over a space X to a bundle (Y

)

over X is a map

with the property that

is a commutative diagram (p

= p

f). The bundle map f is called a bundle isomorphism

and we say that the bundles (Y

) and (Y

) are isomorphic if f is a homeomorphism.

If (Y,p) = (Y

) = (Y

), then a bundle isomorphism is called a bundle automorphism

of (Y,p).

Deﬁnition. A bundle (Y,p) over a space X that is isomorphic to a product bundle is

called a trivial bundle. The bundle is called a locally trivial bundle if for every x Œ X

there is an open neighborhood U of x in X such that (p

-1

(U),pΩp

-1

(U)) is isomorphic

to a trivial bundle over U.

If all locally trivial bundles were trivial bundles, there would be no point in intro-

ducing the concept of bundle. The next example describes a very simple nontrivial

bundle.

7.4.2.1. Example. If we consider P

as the quotient space of S

where antipodal

points are identiﬁed and let p:S

Æ P

be the quotient map, then one can show that

,p) is a locally trivial bundle over P

(Exercise 7.4.2.1). Every ﬁber is the discrete

space consisting of two points. Clearly, (S

,p) is not a trivial bundle because S

is con-

nected and the trivial bundle with ﬁbers consisting of two points would not be.

æÆæ

f: YY

7.4 Homotopy Theory 423

total space

base space

projection

fibers p

–1

(x) ≈ F

Figure 7.24. Basic bundle terminology.

It is the bundles with discrete ﬁbers that interest us in this section. In Section 8.10

we shall look at bundles whose ﬁbers are vector spaces.

Deﬁnition. A covering space for a space X is a locally trivial bundle with base space

X with the property that every ﬁber is a discrete space. The covering is called an

n-fold covering if every ﬁber consists of n points. The bundle automorphisms of a

covering space are called covering transformations.

Example 7.4.2.1 already described a 2-fold covering space. Here are some more

examples.

7.4.2.2. Example. The map

deﬁnes a covering space (R,p) of S

whose ﬁbers

are a countable discrete set of points.

7.4.2.3. Example. Consider the circle S

as a subset of the complex plane C. The

map

deﬁnes a bundle (S

,p) over S

that is an n-fold covering space for S

7.4.2.4. Example. The map

deﬁnes a is a covering space (R

,p) of the torus S

¥ S

That all the total spaces in our examples were manifolds should not be

surprising.

pst t t t t, cos ,sin , cos ,sin .

()

()()()

p: RSSRR

21122

Æ¥Ã ¥

()

p: SS

pt t nn

()

=+ Œ

{}

2p Z

pt t t

()

cos ,sin

p: RSÆ

424 7 Algebraic Topology

7.4.2.5. Theorem. The total space of a covering space of a topological manifold is

a topological manifold.

Proof. This is obvious from the local triviality property of the bundle.

When one works with covering spaces or bundles in general, some of the most

important tools are map-lifting tools.

Deﬁnition. Let (Y,p) be a covering space for a space X and let g:[a,b] Æ X be a con-

tinuous curve. A map g˜ :[a,b] Æ Y is called a lifting of the curve g starting at g˜(a) if

we have a commutative diagram

that is, p

g˜ =g. More generally, given a map f : Z Æ X, any map

f:Z Æ Y is called a

lifting of f if we have a commutative diagram

that is, p

= f.

7.4.2.6. Theorem. (The Path-Lifting Theorem) Let (Y,p) be a covering space for a

space X. Let x

Œ X and y

Œ p

-1

). Then every continuous curve g:[0,1] Æ X lifts

to a unique continuous curve g˜:[0,1] Æ Y that starts at y

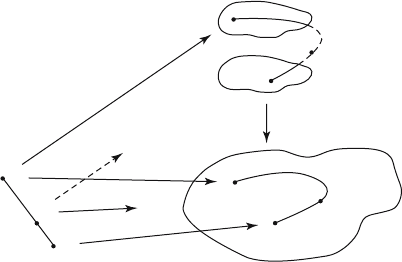
Proof. We sketch a proof of this theorem. It will give the reader a good idea of the

kind of arguments one uses with covering spaces. Figure 7.25 shows what is involved.

æÆæ ,

[]

æÆæ

7.4 Homotopy Theory 425

····

g (t)

–1

(U)

Figure 7.25. Lifting paths.

426 7 Algebraic Topology

The easy case is where one can ﬁnd an open neighborhood U of x

over which the

covering space is trivial and that contains the curve g(t). The set p

-1

(U) will consist of

disjoint open sets in Y that are homeomorphic copies of U. Let V be the one that con-

tains y

and let p

= pΩV. Then g˜ = p

-1

g is the unique curve we seek. For the general

case, we separate the proof into two parts.

We prove uniqueness ﬁrst. Let g˜

and g˜

be two liftings of g that start at y

. Con-

sider the sets

These are obviously disjoint sets whose union is [0,1]. Using continuity, it is easy to

show that both of these sets are open in [0,1]. Since 0 Œ A, A is nonempty. But [0,1]

is connected and so B must be the empty set and we have proved uniqueness.

To prove the existence of a g˜, consider the set

Figure 7.26 should help the reader follow the rest of the argument. Since the cover-

ing space is trivial over an open neighborhood of x

and we know how to lift paths

over such a neighborhoods, the set C will contain a small neighborhood of 0 and

hence, if c is the supremum of C, then 0 < c £ 1. If c = 1, we are done. Assume that

c < 1. Choose a neighborhood U of g(c) over which the covering space is trivial. Choose

e>0, such that [c - 2e,c + 2e] Ã [0,1] and g([c - 2e,c + 2e]) Ã U. By the deﬁnition of

c, there is a lifting

Because the curve gΩ[c - 2e,c + 2e] lies in U it can be lifted to Y, that is, the lifting g˜

can be extended to a lifting of gΩ[0,c + 2e]. This contradicts the fact that c was the

supremum of the set C and so c < 1 is impossible.

ge:, .0c-

[]

Æ X

:,ge0c-

[]

Æ Y

C t there t=Œ

[] []

{}

01 0,,. is a lifting of overg

AB=Œ

[]

()

{}

=Œ

[]

()

{}

t t t and t t t01 01

12 12

˜˜

.gg gg

= g (0)

lifting of g | [c – e, c + 2e]

g (c – e)

g (c + 2e)

g (c)

Figure 7.26. Proving the existence of path

liftings.

The importance of Theorem 7.4.2.6 is not only that every path in the base space

lifts to path in the total space but that the lift is essentially unique, meaning that if

two lifted paths agree at one point, then they agree everywhere. The unique lifting

property generalizes to arbitrary connected spaces not just the interval [0,1]. Another

important lifting theorem is the following:

7.4.2.7. Theorem. (The Homotopy Lifting Theorem) Let (Y,p) be a covering space

for a space X. Let h:Z ¥ [0,1] Æ X be a continuous map. Deﬁne h

:Z Æ X by h

(y) =

h(y,t). If h

is a lifting of h

, then h lifts to a unique continuous map h

:Z ¥ [0,1] Æ Y

so that h

(y,0) = h

(y).

Proof. See [Jäni84]. Figure 7.27 tries to indicate the relationship between the various

maps.

7.4.2.8. Corollary. (The Monodromy Lemma) Let (Y,p) be a covering space for a

space X. Let g

, g

:[0,1] Æ X be two continuous curves that start at the same point x

and end at the same point x

, that is, x

(0) =g

(0) and x

(1) =g

(1). Assume

that g

and g

are homotopic by a homotopy h that ﬁxes the endpoints, that is, h(t,0)

= x

and h(t,1) = x

, for all t Œ [0,1]. If, g˜

, g˜

:[0,1] Æ Y are liftings of g

and g

, respec-

tively, that start at the same point in Y, then g˜

and g˜

will end at the same point, that

is, g˜

(1) =g˜

(1).

Proof. This is an easy consequence of Theorem 7.4.2.7.

Corollary 7.4.2.8 is an important uniqueness type theorem. It says that if one lifts

two homotopic paths that start and end at the same point, then the lifted paths will

also end at the same point if they start at the same point.

The next two results describe some relationships between the fundamental groups

of the total and base space of a covering space.

7.4.2.9. Theorem. Let (Y,p) be a covering space for a space X. Let x

Œ X and y

-1

). Then the induced homomorphism

()

:, ,pp

10 10

Yy Xx

7.4 Homotopy Theory 427

Z ¥ 0

Z ¥ 1

Z ¥ [0,1]

h(z,t)

Figure 7.27. Lifting a homotopy.

is one-to-one.

Proof. See [Mass67] or [Jäni84]. Basically, if an element [f] maps to 0, then the map

f is homotopic to a constant in X and this homotopy lifts to a homotopy between f

and the constant map in Y.

A natural question is if y

Œ p

-1

), then what is the relation between the sub-

groups p

(Y,y

)) and p

(Y,y

)) in p

(X,x

)? There is an easy answer.

7.4.2.10. Theorem. Let (Y,p) be a covering space for a space X and let x

Œ X. If Y

is connected, then the subgroups p

(Y,y

)) in p

(X,x

) as y

ranges over the points

in p

-1

) generate a conjugacy class of subgroups in p

(X,x

Proof. See [Mass67]. The result follows easily from the following observations. Let

, y

Œ p

-1

). Let a˜ : [0,1] Æ Y be a curve with a˜ (0) = y

and a˜ (1) = y

. The curve a

= p

a˜ : [0,1] Æ X is a loop at x

. If [g˜] Œp

(Y,y

), then deﬁne m˜ : [0,1] Æ Y by

Now, set g=p

g˜ and m=p

m˜. It is easy to show that [m˜] Œp

(Y,y

) and [m] = [a]

-1

[g][a]

Œp

(X,x

). See Figure 7.28.

Next, we would like to classify covering spaces. Let (Y,p) be a covering space for

a space X and let x

Œ X and y

Œ p

-1

). First, we shall answer the question about

when maps from some arbitrary space Z into X lifts to a map into Y. Let z

Œ Z. The

speciﬁc question is, given a map f : (Z,z

) Æ (X,x

), when does a lifting f

: (Z,z

) Æ

(Y,y

) exist? In terms of diagrams, we are given f and p and are looking for an f

that

will produce a commutative diagram

,,,

,,.

tt t

()

428 7 Algebraic Topology

Figure 7.28. How loops in the total space project to

conjugate loops.