Афонин А.В., Ньюпорт Р.К., Поляков В.С. и др. Основы инфракрасной термографии

Подождите немного. Документ загружается.

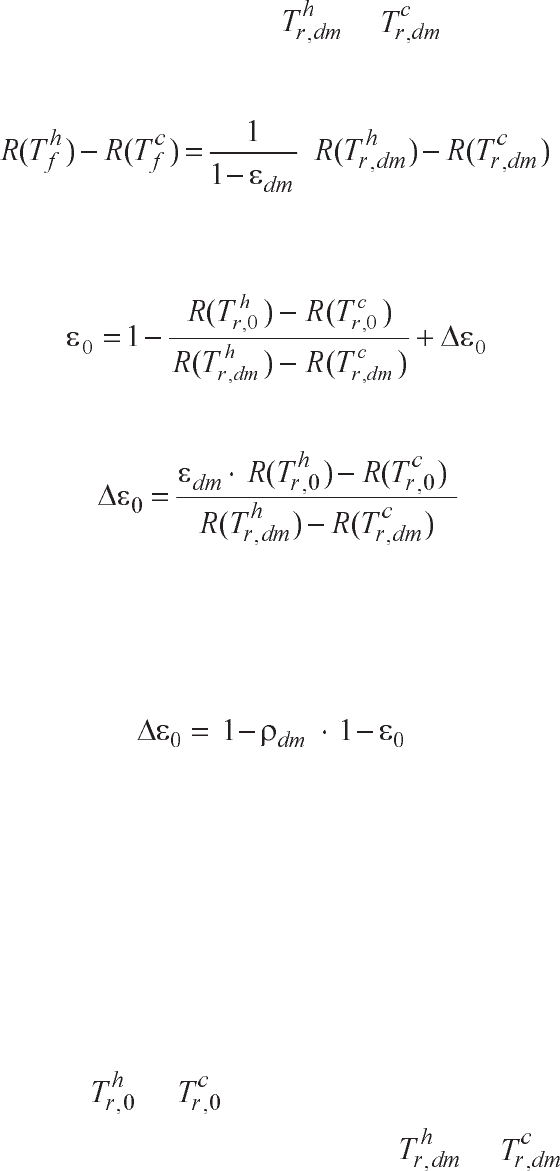
211

îò íèõ ýôôåêòèâíûå òåìïåðàòóðû

è . Òîãäà ðàçíîñòü ñâåòè-

ìîñòåé ôîíîâîé çàñâåòêè ðàâíà





. (4.11)

Ïîäñòàâëÿÿ (4.11) â (4.10), ïîëó÷èì

; (4.12)





. (4.13)

Åñëè ïðåíåáðå÷ü ïðè âû÷èñëåíèÿõ ïîñëåäíèì ÷ëåíîì (4.12), òî

åãî âåëè÷èíà áóäåò îïðåäåëÿòü ïîãðåøíîñòü èçìåðåíèÿ êîýôôèöèåíòà

èçëó÷åíèÿ îáúåêòà e

âñëåäñòâèå e

¹ 0. Ïîñêîëüêó èç (4.13) ñëåäóåò, ÷òî



, (4.14)

òî íå òðóäíî îòûñêàòü ýòó ïîãðåøíîñòü. Åñëè èñïîëüçóåòñÿ äèôôóç-

íîå çåðêàëî ñ êîýôôèöèåíòîì îòðàæåíèÿ r

= 0,9 , òî ïðè e

=0,8 ïî-

ãðåøíîñòü De

= 0,02. Ïîýòîìó, ÷åì ìåíüøå êîýôôèöèåíò èçëó÷åíèÿ

îáúåêòà, òåì òî÷íåå íóæíû ðàñ÷åòû, è âåëè÷èíîé De

ïðåíåáðåãàòü íå

ðåêîìåíäóåòñÿ.

Òàêèì îáðàçîì, îïðåäåëåíèå êîýôôèöèåíòà èçëó÷åíèÿ äèôôóçíîé

èëè çåðêàëüíî-äèôôóçíîé ïîâåðõíîñòè ïðîèçâîäèòñÿ ïî ÷åòûðåì èç-

ìåðåíèÿì òåïëîâèçîðà ðàäèàöèîííûõ òåìïåðàòóð îáúåêòà èëè èññëå-

äóåìîãî ìàòåðèàëà

è ïðè «ãîðÿ÷åé» è «õîëîäíîé» ïîëóñôå-

ðè÷åñêèõ çàñâåòêàõ, è äèôôóçíîãî çåðêàëà

è .

Íóæíî îòìåòèòü, ÷òî çíà÷åíèåì êîýôôèöèåíòà èçëó÷åíèÿ äëÿ çåð-

êàëüíî-äèôôóçíîé ïîâåðõíîñòè ìîæíî ïîëüçîâàòüñÿ ïðè èçìåðåíèÿõ

òåìïåðàòóðû, êîãäà â îêðóæàþùåé ñðåäå îòñóòñòâóþò ëîêàëüíûå èñ-

òî÷íèêè èçëó÷åíèÿ, ñïîñîáíûå âûçâàòü ïîâûøåííûé óðîâåíü ÿðêîñòè

îòðàæåííîãî èçëó÷åíèÿ â íàïðàâëåíèè òåïëîâèçîðà, ò.å. èçëó÷åíèå îò

ýòèõ áîêîâûõ èñòî÷íèêîâ íåîáõîäèìî ýêðàíèðîâàòü.

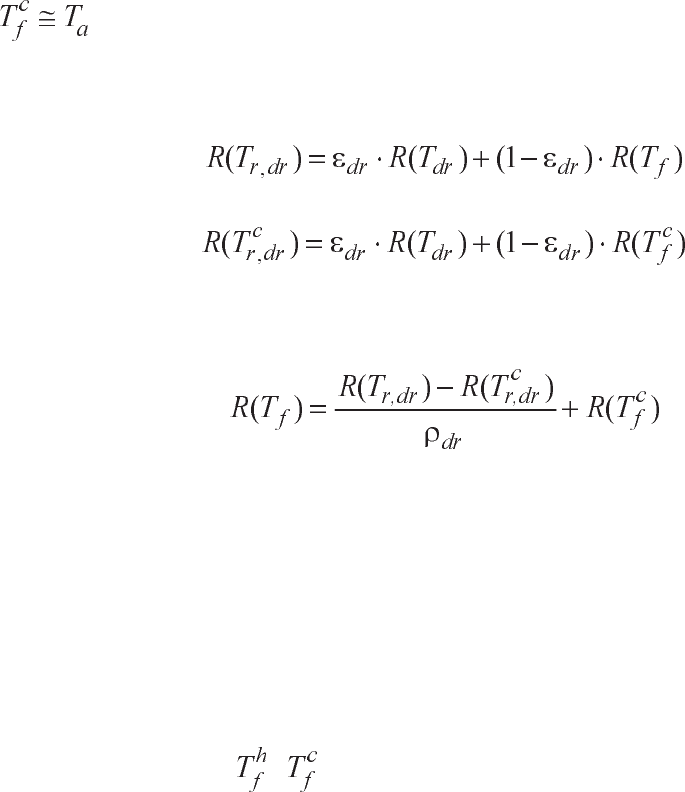
212

4.2. Îïðåäåëåíèå ýôôåêòèâíîé òåìïåðàòóðû

ïîëóñôåðè÷åñêîé ôîíîâîé çàñâåòêè

Îïðåäåëåíèå ýôôåêòèâíîé òåìïåðàòóðû ïîëóñôåðè÷åñêîé ôîíî-

âîé çàñâåòêè ìîæíî ïðîâîäèòü ñ ïîìîùüþ äèôôóçíî îòðàæàþùåãî

ïëîñêîãî çåðêàëà ïî èçìåðåíèÿì òåïëîâèçîðà, åñëè óäàåòñÿ ñîçäàòü

äèôôóçíîå çåðêàëî ñ âûñîêèì êîýôôèöèåíòîì èçëó÷åíèÿ è ñ ïðåíåá-

ðåæèìî ìàëîé çåðêàëüíîé ñîñòàâëÿþùåé îòðàæåíèÿ. Òîãäà T

= T

Ñîçäàíèå òàêîãî çåðêàëà â òåïëîâîé ÈÊ îáëàñòè ñïåêòðà  äîðîãîñ-

òîÿùåå ìåðîïðèÿòèå, ïîýòîìó ìîæíî èñïîëüçîâàòü äèôôóçíûé îòðà-

æàòåëü ñ ìåíüøèì êîýôôèöèåíòîì îòðàæåíèÿ, íî çàòî ñ ãàðàíòèðî-

âàííîé ìèíèìàëüíîé çåðêàëüíîé ñîñòàâëÿþùåé îòðàæåíèÿ.

Îïðåäåëåíèå ýôôåêòèâíîé òåìïåðàòóðû ïîëóñôåðè÷åñêîé ôîíî-

âîé çàñâåòêè ïðîèçâîäèòñÿ ìåòîäîì ñðàâíåíèÿ ñâåòèìîñòåé, ðåãèñò-

ðèðóåìûõ òåïëîâèçîðîì ïðè íàòóðíîì ôîíå, îñâåùàþùåì äèôôóç-

íûé îòðàæàòåëü ïðè òåìïåðàòóðå T

, è ïðè ôîíå, òåìïåðàòóðà êîòîðîãî

ïðèìåðíî ðàâíà òåìïåðàòóðå îêðóæàþùåãî âîçäóõà. Òàêóþ

òåìïåðàòóðó èìååò «õîëîäíûé» èñòî÷íèê ïîëóñôåðè÷åñêîé çàñâåòêè.

Çàïèøåì óðàâíåíèÿ ñâåòèìîñòåé äèôôóçíîãî îòðàæåíèÿ

; (4.15)

. (4.16)

Ðåøàÿ ýòè óðàâíåíèÿ ñîâìåñòíî, ïîëó÷èì

. (4.17)

Òåìïåðàòóðû èçìåðÿþòñÿ òåïëîâèçîðîì òîëüêî ïðè ðàçíîé ôîíîâîé

çàñâåòêå. Ïîãðåøíîñòè îïðåäåëåíèÿ T

âîçðàñòàþò ïðè óìåíüøåíèè

=1-e

, ïîýòîìó åãî âåëè÷èíà äîëæíà áûòü áîëåå ~0,5. Êîýôôèöè-

åíò èçëó÷åíèÿ äèôôóçíîãî îòðàæàòåëÿ îïðåäåëÿåòñÿ òàê æå, êàê è ó

îáúåêòà ñ èñïîëüçîâàíèåì äèôôóçíîãî çåðêàëà è ïàðû èçëó÷àòåëåé

«ãîðÿ÷åãî» è «õîëîäíîãî». Íóæíî îòìåòèòü, ÷òî ê äèôôóçíîìó çåðêà-

ëó ñ âûñîêèì êîýôôèöèåíòîì îòðàæåíèÿ r

, èñïîëüçóåìîìó ïðè êîí-

òðîëå òåìïåðàòóð

, è óñòàíàâëèâàåìîìó â óñòðîéñòâî â ïëîñêî-

213

ñòè ðàçìåùåíèÿ êîíòðîëèðóåìîãî îáúåêòà, íå ïðåäúÿâëÿþòñÿ âûñîêèå

òðåáîâàíèÿ ïî î÷åíü ìàëîé âåëè÷èíå çåðêàëüíîé ñîñòàâëÿþùåé, ïî-

ñêîëüêó â óñòðîéñòâå ñîçäàåòñÿ äîâîëüíî ðàâíîìåðíàÿ ïîëóñôåðè÷åñ-

êàÿ çàñâåòêà çåðêàëà.

4.3. Îïðåäåëåíèå ñèñòåìàòè÷åñêèõ ïîãðåøíîñòåé

Ïðîâåðêà ãðàäóèðîâî÷íîé õàðàêòåðèñòèêè íåêîòîðûõ òèïîâ òåï-

ëîâèçîðîâ ïîêàçàëà, ÷òî îíà íå ïîñòîÿííà è èìååò ìåñòî òåìïåðàòóð-

íûé äðåéô åå ïàðàìåòðîâ. Ýêñïåðèìåíòàëüíûå èññëåäîâàíèÿ ïîçâî-

ëèëè íàéòè íàèáîëåå óäîáíûé ñïîñîá åå êîíòðîëÿ ñ ïîìîùüþ

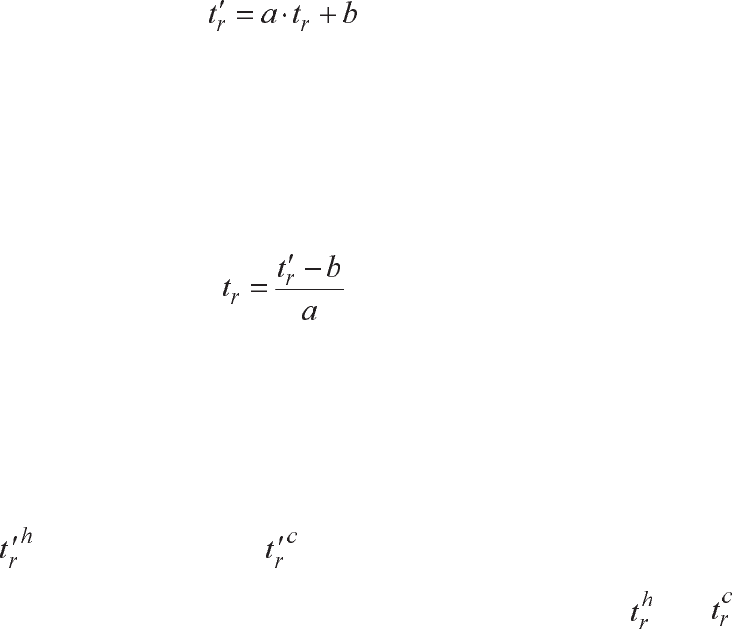
îïðåäåëåíèÿ ðåãðåññèè èçìåðÿåìîé ýôôåêòèâíîé òåìïåðàòóðû t¢

, ñî-

äåðæàùåé ñèñòåìàòè÷åñêèå ïîãðåøíîñòè, íà èñòèííóþ ýôôåêòèâíóþ

òåìïåðàòóðó t

èìèòàòîðà ÷åðíîãî òåëà, èçìåðÿåìóþ êîíòàêòíûì òåð-

ìîäàò÷èêîì, èìåþùèì øêàëó 0,1°. Ýêñïåðèìåíòû ïîêàçàëè, ÷òî ëè-

íåéíàÿ ðåãðåññèîííàÿ çàâèñèìîñòü ñîõðàíÿåò ñâîè ïàðàìåòðû â øè-

ðîêîì äèàïàçîíå èçìåíåíèÿ òåìïåðàòóð îáúåêòà.

Çàïèøåì óðàâíåíèå ðåãðåññèè

, (4.18)

ãäå a, b  ïàðàìåòðû óðàâíåíèÿ, çàâèñÿùèå îò òåìïåðàòóðû îêðóæàþ-

ùåé ñðåäû. Èç ýòîãî óðàâíåíèÿ ìîæíî îïðåäåëèòü èñòèííóþ ýôôåê-

òèâíóþ òåìïåðàòóðó îáúåêòà, è, òåì ñàìûì, êîìïåíñèðîâàòü ñèñòåìà-

òè÷åñêèå ïîãðåøíîñòè

. (4.19)

Äëÿ ýêñïåðèìåíòàëüíîãî îïðåäåëåíèÿ ýòèõ ïàðàìåòðîâ íåîáõîäèìî èç-

ìåðåíèå â íàòóðíûõ óñëîâèÿõ, ïî êðàéíåé ìåðå, äâóõ çíà÷åíèé òåìïå-

ðàòóð èìèòàòîðà ÷åðíîãî òåëà. Ïîëîæèì, ÷òî â íàòóðíûõ óñëîâèÿõ ó

íàñ ðåàëèçîâàíà âîçìîæíîñòü èçìåðåíèÿ ýôôåêòèâíîé òåìïåðàòóðû

«ãîðÿ÷åãî» (

) è «õîëîäíîãî» ( ) ÷åðíûõ òåë ñ ïîìîùüþ òåïëîâè-

çîðà, à òàêæå èçìåðåíèÿ èñòèííûõ ýôôåêòèâíûõ òåìïåðàòóð (

) è ( )

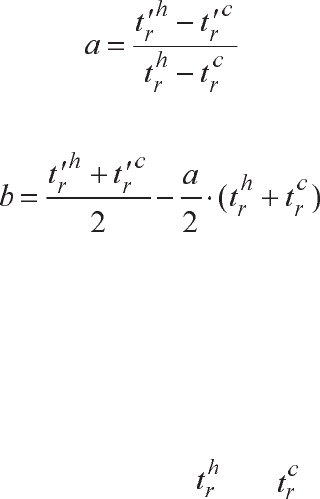
214

ýòèõ òåë ñ ïîìîùüþ êîíòàêòíîãî òåðìîäàò÷èêà. Òîãäà ïàðàìåòðû óðàâ-

íåíèé ìîãóò áûòü îïðåäåëåíû

; (4.20)

. (4.21)

Ïðè a =1 è b=0 ñèñòåìàòè÷åñêèå ïîãðåøíîñòè òåðìîðàäèîìåòðè-

÷åñêèõ èçìåðåíèé îòñóòñòâóþò. Ïîíÿòíî, ÷òî îäíîé ïàðû òî÷åê âñëåä-

ñòâèå ñëó÷àéíûõ ïîãðåøíîñòåé èçìåðåíèÿ íåäîñòàòî÷íî. Íåîáõîäè-

ìî ïîëó÷èòü, ïî êðàéíåé ìåðå, îò 3 äî 15 è áîëåå ïàð òî÷åê è çàòåì

ïðîâåñòè îñðåäíåíèå ïî âûáîðêå. Ìèíèìàëüíîé âûáîðêîé ìîæíî

îáîéòèñü, åñëè ðàçíîñòü òåìïåðàòóð (

) è ( ) áóäåò ïåðåêðûâàòü âåñü

äèàïàçîí èçìåðÿåìûõ òåìïåðàòóð îáúåêòà, è ñðåäíåêâàäðàòè÷åñêàÿ ïî-

ãðåøíîñòü èçìåðåíèÿ ýôôåêòèâíîé òåìïåðàòóðû òåïëîâèçîðà íå ïðåâû-

øàåò òðåáóåìóþ ñðåäíåêâàäðàòè÷åñêóþ ïîãðåøíîñòü åå èçìåðåíèé.

Óñòðîéñòâî äëÿ ðåàëèçàöèè âûøå ðàññìîòðåííûõ ñïîñîáîâ, íà-

çûâàåìîå êàëèáðàòîðîì, ïðåäñòàâëÿåò ñîáîé çàìêíóòóþ ïëîñêîñòü â

âèäå ïîëóñôåðû, ñîäåðæàùåé îòâåðñòèå â âåðõíåé ÷àñòè, ÷åðåç êîòî-

ðîå ñ ïîìîùüþ òåïëîâèçîðà èìååòñÿ âîçìîæíîñòü íàáëþäàòü ðàçëè÷-

íûå ïîâåðõíîñòè. Îïòè÷åñêàÿ ñõåìà óñòðîéñòâà ïðèâåäåíà íà ðèñ. 4.2.

Â ïëîñêîñòè A óñòàíàâëèâàþòñÿ:

 ýëåìåíòû ñ âûñîêèì êîýôôèöèåíòîì èçëó÷åíèÿ äëÿ êàëèáðîâ-

êè òåïëîâèçîðà, ïðèíèìàþùèå ïðè íåêîòîðîé âûäåðæêå òåìïåðàòóðó

êîëüöà íàãðåâàòåëåé, ðàñïîëîæåííîãî çà äèàìåòðîì d

;

 äèôôóçíîå çåðêàëî, äèôôóçíûé îòðàæàòåëü è ïëîñêîñòü êîíò-

ðîëèðóåìîãî îáúåêòà.

«Ãîðÿ÷àÿ» çàñâåòêà ñîçäàåòñÿ êîëüöîì, èçëó÷åíèå êîòîðîãî îòðà-

æàåòñÿ âíóòðåííåé çåðêàëüíîé ïîâåðõíîñòüþ ïîëóñôåðû íà îáñëåäó-

åìûé îáúåêò. «Õîëîäíàÿ» çàñâåòêà ìîæåò ôîðìèðîâàòüñÿ òàêèì æå

óñòðîéñòâîì áåç íàãðåâà. Òàêèì îáðàçîì, äëÿ áûñòðîé è ýôôåêòèâíîé

ðàáîòû íåîáõîäèìî èìåòü äâà êàëèáðàòîðà. Ãåîìåòðè÷åñêèå ðàçìåðû

óñòðîéñòâ äîëæíû óäîâëåòâîðÿòü ñîîòíîøåíèÿì

215

; (4.22)

, (4.23)

ãäå a

 ìãíîâåííûé óãîë ïîëÿ çðåíèÿ â ðàäèàíàõ, D

 äèàìåòð

âõîäíîãî çðà÷êà òåïëîâèçîðà, r  ðàäèóñ ïîëóñôåðû.

Òåìïåðàòóðà ýëåìåíòîâ ñ âûñîêèì êîýôôèöèåíòîì èçëó÷åíèÿ äëÿ

êàëèáðîâêè òåïëîâèçîðà êîíòðîëèðóåòñÿ ÷óâñòâèòåëüíûì ýëåìåíòîì

êîíòðîëüíîãî òåðìîäàò÷èêà, äåðæàòåëü êîòîðîãî âñòàâëÿåòñÿ â îòâåð-

ñòèå íà âåðøèíå ïîëóñôåðû.

Ïðèìåíåíèå ïîëóñôåðû ñ çåðêàëüíûì âíóòðåííèì ïîêðûòèåì

ïîçâîëèò ìàêñèìàëüíî óâåëè÷èòü ïîòîê çàñâåòêè ïðè ìèíèìàëüíîé

èçëó÷àþùåé ïîâåðõíîñòè íàãðåâàòåëÿ. Êðîìå òîãî, ýòî ðåøåíèå ñíè-

æàåò òðåáîâàíèÿ ê òåïëîèçîëÿöèè óñòðîéñòâà. Òàêèì îáðàçîì, òàêîé

êàëèáðàòîð ïîçâîëÿåò çíà÷èòåëüíî, (à, èíîãäà, ðàäèêàëüíî) ïîâûñèòü

òî÷íîñòü èçìåðåíèé òåðìîäèíàìè÷åñêîé òåìïåðàòóðû îáúåêòîâ â øè-

ðîêîì äèàïàçîíå òåìïåðàòóð îêðóæàþùåé ñðåäû ñ ïîìîùüþ òåðìî-

ãðàôè÷åñêèõ òåïëîâèçîðîâ.

Ðèñ. 4.2. Îïòè÷åñêàÿ ñõåìà êàëèáðàòîðà

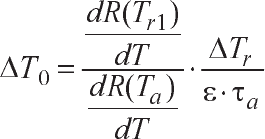
216

4.4. Ïëàíèðîâàíèå òåðìîðàäèîìåòðè÷åñêèõ èçìåðåíèé

Ïîä ïëàíèðîâàíèåì òåðìîðàäèîìåòðè÷åñêèõ èçìåðåíèé ïîíèìà-

åòñÿ ñîâîêóïíîñòü ïîäãîòîâèòåëüíîé ðàáîòû, âêëþ÷àþùàÿ:

 âûÿâëåíèå ñïåöèôèêè ýêñïåðèìåíòà è îïðåäåëåíèå âçàèìîñâÿçè

òåìïåðàòóðû ïîâåðõíîñòè îáúåêòà è êîíòðîëèðóåìûõ òåïëîôèçè÷åñ-

êèõ ïàðàìåòðîâ;

 îïðåäåëåíèå òðåáîâàíèé è âûáîð èçìåðèòåëüíîé àïïàðàòóðû;

 îïðåäåëåíèå òðåáîâàíèé ê òî÷íîñòè èçìåðåíèé ýôôåêòèâíîé è

òåðìîäèíàìè÷åñêîé òåìïåðàòóðû;

 âûáîð óñëîâèé ïðîâåäåíèÿ òåïëîâèçèîííîé ñúåìêè è îïðåäåëå-

íèå íåîáõîäèìîñòè ó÷åòà ñîïóòñòâóþùèõ ïàðàìåòðîâ.

Î÷åâèäíî, ÷òî ïëàíèðîâàíèå ýêñïåðèìåíòà äîëæíî íîñèòü êîíêðåò-

íûé õàðàêòåð, ñâÿçàííûé â ïåðâóþ î÷åðåäü ñî ñïåöèôèêîé ðåøàåìîé ïî-

ñðåäñòâîì òåðìîìåòðè÷åñêèõ èçìåðåíèé òåïëîôèçè÷åñêîé çàäà÷è. Ïî-

ëó÷åííûå ïðè ýòîì äàííûå äîëæíû ëå÷ü â îñíîâó êîíêðåòíîé ìåòîäèêè

ïðîâåäåíèÿ ýêñïåðèìåíòà è èçìåðåíèé îïåðàòîðà òåïëîâèçèîííîé àïïà-

ðàòóðû, à òàêæå ìåòîäèêè îáðàáîòêè ðåçóëüòàòîâ ýêñïåðèìåíòà.

4.4.1. ÈÇÌÅÐÅÍÈÅ ÌÀËÛÕ ÒÅÌÏÅÐÀÒÓÐÍÛÕ ÊÎÍÒÐÀÑÒÎÂ

ÍÀ

ÓÐÎÂÍÅ ÒÅÌÏÅÐÀÒÓÐ ÎÊÐÓÆÀÞÙÅÉ ÑÐÅÄÛ

Ìíîãèå çàäà÷è êîíòðîëÿ â ýíåðãåòèêå ïîñòðîåíû íà èçìåðåíèè ðàç-

íîñòè òåìïåðàòóð êîíòðîëèðóåìûõ ýëåìåíòîâ, ÷üè õàðàêòåðèñòèêè òðå-

áóåòñÿ îïðåäåëèòü, è ýëåìåíòîâ ñ èçâåñòíûìè õàðàêòåðèñòèêàìè. Ýëå-

ìåíòû ñ èçâåñòíûìè õàðàêòåðèñòèêàìè íàçîâåì îïîðíûìè èëè áàçîâûìè.

Ðàññìîòðèì ñïåöèôèêó ïðèìåíåíèÿ òåðìîãðàôè÷åñêîé àïïàðàòó-

ðû äëÿ ðåøåíèÿ ýòèõ çàäà÷. Äëÿ ïðîñòîòû èçëîæåíèÿ ðàññìîòðèì ñëó-

÷àé, êîãäà òåìïåðàòóðà îïîðíîãî ýëåìåíòà î÷åíü áëèçêà ê òåìïåðàòó-

ðå îêðóæàþùåãî âîçäóõà.

Èñïîëüçóÿ óðàâíåíèå (3.21), çàïèøåì óðàâíåíèå ñâÿçè êîíòðàñ-

òîâ òåðìîäèíàìè÷åñêîé è ðàäèàöèîííîé òåìïåðàòóð, èçìåðÿåìûõ â ýê-

ñïåðèìåíòå, ó÷èòûâàÿ, ÷òî òåðìîäèíàìè÷åñêàÿ òåìïåðàòóðà îïîðíîãî

ýëåìåíòà ðàâíà Ò

=Ò

. (4.24)

217

Äëÿ óäîáñòâà àíàëèçà îïðåäåëèì ðàäèàöèîííóþ òåìïåðàòóðó îïîðíî-

ãî ýëåìåíòà T

òàêæå ÷åðåç òåìïåðàòóðó âîçäóõà ñ ïîìîùüþ óðàâíå-

íèÿ (3.23), ïîëàãàÿ, ÷òî T

. (4.25)

Äàëüíåéøèå óïðîùåíèÿ ïîçâîëÿþò çàìåòèòü, ÷òî

@ T

- (T

- T

) × t

× (1- e). (4.26)

Îòêëîíåíèå ðàäèàöèîííîé òåìïåðàòóðû îò òåìïåðàòóðû âîçäóõà âîç-

ðàñòàåò ñ óâåëè÷åíèåì ðàçíîñòè òåìïåðàòóð ôîíîâîé çàñâåòêè è âîç-

äóõà è óìåíüøåíèåì êîýôôèöèåíòà èçëó÷åíèÿ.

Âûáîð îáëàñòè ñïåêòðà, â êîòîðîé íàèáîëåå ýôôåêòèâíî ïðîèçâî-

äèòñÿ êîíòðîëü ìàëûõ òåìïåðàòóðíûõ êîíòðàñòîâ, ñëåäóåò ïðîèçâî-

äèòü íà îñíîâå êðèòåðèåâ, ñâÿçàííûõ ñ óñëîâèÿìè îáíàðóæåíèÿ ìà-

ëûõ òåïëîâûõ êîíòðàñòîâ, òî÷íîñòüþ èõ èçìåðåíèé è òåõíî-

ëîãè÷íîñòüþ èçìåðåíèé. Ïîä òåõíîëîãè÷íîñòüþ èçìåðåíèé ïîíèìà-

åòñÿ áîëüøîå ðàçíîîáðàçèå óñëîâèé ñúåìêè ïðè ìèíèìàëüíîì ÷èñëå

êîíòðîëèðóåìûõ ñîïóòñòâóþùèõ ïàðàìåòðîâ.

Çà êðèòåðèé ýôôåêòèâíîñòè îáíàðóæåíèÿ ìàëûõ òåïëîâûõ êîí-

òðàñòîâ öåëåñîîáðàçíî ïðèíÿòü îòíîñèòåëüíóþ âåëè÷èíó èçìåíåíèÿ

ñèãíàëà íà âûõîäå òåïëîâèçîðà (â òîì ÷èñëå íà äèñïëåå îïåðàòîðà)

ïðè íàáëþäåíèè ìàëûõ êîíòðàñòîâ.

. (4.27)

Ýòó âåëè÷èíó ïðè DT

= 1° íàçûâàþò åùå îòíîñèòåëüíûì äèôôå-

ðåíöèàëüíûì êîíòðàñòîì. ×åì áîëüøå îòíîñèòåëüíàÿ âåëè÷èíà èçìåíå-

íèÿ ñèãíàëà, òåì âûøå âèçóàëèçèðóåìûé êîíòðàñò ìåæäó ýëåìåíòàìè

îáúåêòà ñ ðàçíîé òåìïåðàòóðîé.

Ïðè èçìåðåíèè ìàëûõ ñèãíàëîâ îñíîâíóþ ðîëü èãðàþò øóìû òåï-

ëîâèçîðà, à òàêæå ïîãðåøíîñòè êîíòðîëÿ ïðîïóñêàíèÿ àòìîñôåðû è

êîýôôèöèåíòà èçëó÷åíèÿ.

218

Ïîãðåøíîñòè îïðåäåëåíèÿ êîíòðàñòà òåðìîäèíàìè÷åñêîé òåìïå-

ðàòóðû âñëåäñòâèå ïîãðåøíîñòè îöåíêè ïðîïóñêàíèÿ è êîýôôèöèåí-

òà èçëó÷åíèÿ ìîæíî çàïèñàòü

; (4.28)

, (4.29)

ãäå dt

= (1- t

) × Y

, de = (1- e) × Y

Ñðåäíåêâàäðàòè÷åñêîå îòêëîíåíèå ïîãðåøíîñòè èçìåðåíèÿ êîí-

òðàñòà DÒ

èç-çà øóìîâ îïòèêî-ýëåêòðîííîãî òðàêòà òåïëîâèçîðà, âå-

ëè÷èíà êîòîðûõ õàðàêòåðèçóåòñÿ øóìîâîé ýêâèâàëåíòíîé ðàçíîñòüþ

òåìïåðàòóð DT

NET

, ìîæåò áûòü ðàññ÷èòàíî ïî ôîðìóëå

. (4.30)

Àðãóìåíò Ò

ÿâëÿåòñÿ òåìïåðàòóðîé À×Ò, ïðè êîòîðîé ïðîâîäÿò

îïðåäåëåíèå DT

NET

. Îáû÷íî îíà ñîñòàâëÿåò 300°Ê.

Êîëè÷åñòâåííûé àíàëèç ïðîâåäåì íà ïðèìåðå êîíòðàñòà òåìïå-

ðàòóð ôàðôîðîâûõ ïîêðûøåê è èçîëÿòîðîâ â äâóõ ñïåêòðàëüíûõ îáëàñ-

òÿõ 3,55,5 è 812 ìêì. Êîýôôèöèåíòû îòðàæåíèÿ ãëàçóðèðîâàííîãî

ôàðôîðà ñîñòàâëÿþò äëÿ äëèí âîëí 4,5 è 9 ìêì r

=0,05, ïîýòîìó

êîýôôèöèåíòû èçëó÷åíèÿ â äâóõ îáëàñòÿõ ñïåêòðà ìîæíî ïðèíÿòü ðàâ-

íûìè e

=0,95. Äëÿ íåãëàçóðèðîâàííîãî ôàðôîðà â êîðîòêîâîëíî-

âîé îáëàñòè ïðè l=4,5 ìêì r

=0,1, e

=0,9 , à â äëèííîâîëíîâîé îáëà-

ñòè ïðè l=9 ìêì r

=0,5, ïîýòîìó e

=0,5. Ðàñ÷åòû ïðîâîäèëèñü ïðè

òåìïåðàòóðàõ âîçäóõà Ò

=260°Ê è 290°Ê, õàðàêòåðíûõ äëÿ çèìû è ëåòà,

ïðè îòíîñèòåëüíîé âëàæíîñòè àòìîñôåðû 70%. Êîíòðàñò òåðìîäèíà-

ìè÷åñêîé òåìïåðàòóðû çàäàâàëñÿ ðàâíûì DÒ

=1°. Ðàñ÷åò ïðîâîäèëñÿ

äëÿ òðàññ, ðàâíûõ L=5, 20, 50 è 100 ì. Îòíîñèòåëüíûå ïîãðåøíîñòè

îïðåäåëåíèÿ ïðîïóñêàíèÿ è êîýôôèöèåíòà èçëó÷åíèÿ Y

= Y

=0,1.

Ðåçóëüòàòû ðàñ÷åòà ïðèâåäåíû â òàáëèöàõ 4.54.7.

219

Â òàáëèöàõ ïîãðåøíîñòè èçìåðåíèé êîíòðàñòà òåðìîäèíàìè÷åñ-

êîé òåìïåðàòóðû ïðèâåäåíû â ãðàäóñàõ.

Èç ïðèâåäåííûõ ðàñ÷åòîâ âèäíî, ÷òî ëó÷øèå óñëîâèÿ ïî îáíàðó-

æåíèþ ñëàáûõ òåïëîâûõ êîíòðàñòîâ èìåþò ìåñòî â êîðîòêîâîëíîâîé

îáëàñòè. Ïðè îäèíàêîâûõ êîýôôèöèåíòàõ èçëó÷åíèÿ ìàòåðèàëà ýòî

èìååò ìåñòî äî ~100 ì. Äàëåå èç-çà çíà÷èòåëüíîé ðàçíèöû ïðîïóñêà-

íèÿ àòìîñôåðû óñëîâèÿ îáíàðóæåíèÿ â êîðîòêîâîëíîâîé è äëèííî-

âîëíîâîé îáëàñòÿõ ñòàíîâÿòñÿ áëèçêèìè äðóã ê äðóãó.

Ïîãðåøíîñòü èçìåðåíèÿ êîíòðàñòà òåðìîäèíàìè÷åñêîé òåìïåðà-

òóðû âñëåäñòâèå ïîãðåøíîñòè îöåíêè ïðîïóñêàíèÿ àòìîñôåðû dDÒ

0,t

ïðåíåáðåæèìî ìàëà íà ðàññìàòðèâàåìûõ òðàññàõ â îáëàñòè ñïåêòðà 812 ìêì,

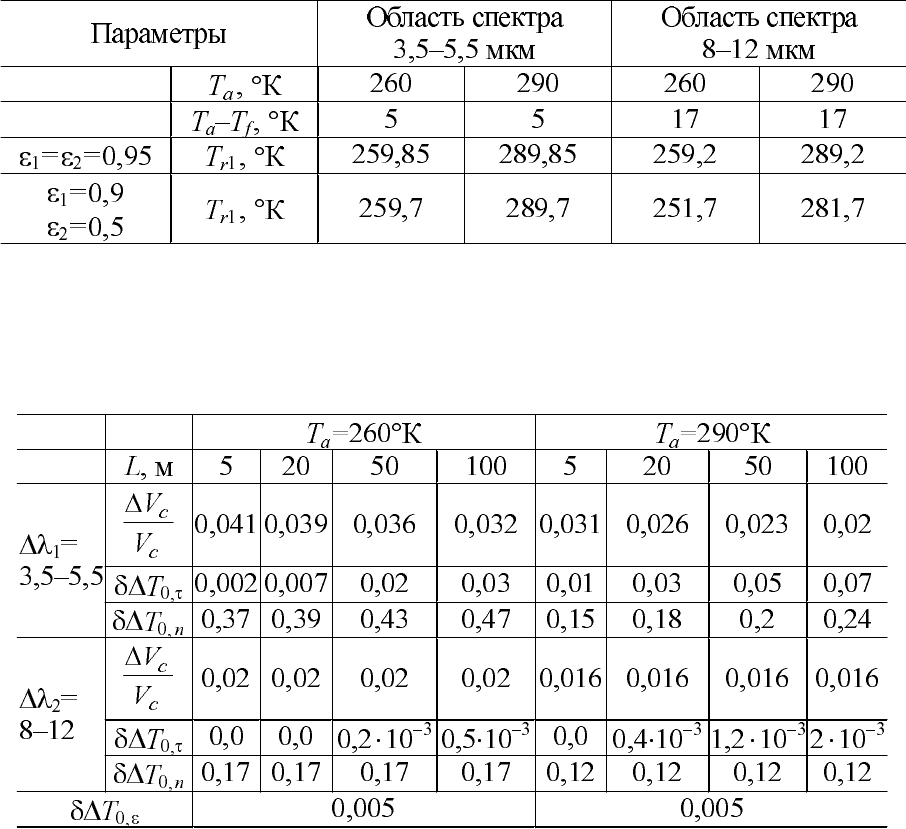
Òàáëèöà 4.5.

Ðàäèàöèîííûå òåìïåðàòóðû ôàðôîðà

Òàáëèöà 4.6.

Îòíîñèòåëüíûé êîíòðàñò ñèãíàëà è ïîãðåøíîñòè èçìåðåíèé êîíòðàñ-

òà òåðìîäèíàìè÷åñêîé òåìïåðàòóðû DÒ

=1° ãëàçóðèðîâàííîãî

ôàðôîðà, e

= e

=0,95

220

íî çàìåòíà â îáëàñòè ñïåêòðà 3,55,5 ìêì ïðè óñëîâèè, ÷òî

ïðîçðà÷íîñòü àòìîñôåðû ó÷èòûâàåòñÿ ïðè îáðàáîòêå ðåçóëüòàòîâ èç-

ìåðåíèé. Åñëè ïðîçðà÷íîñòü àòìîñôåðû íå ó÷èòûâàåòñÿ, ýòà ïîãðåø-

íîñòü âîçðàñòàåò íà ïîðÿäîê è ìîæåò ñòàòü íåäîïóñòèìî áîëüøîé ïðè

îïðåäåëåííûõ óñëîâèÿõ èçìåðåíèé.

Îñíîâíîé âêëàä â ïîãðåøíîñòü èçìåðåíèé ìàëûõ êîíòðàñòîâ âíî-

ñèò ñîñòàâëÿþùàÿ dDÒ

0,n

, îáóñëîâëåííàÿ øóìàìè îïòèêî-ýëåêòðîí-

íîãî òðàêòà òåïëîâèçîðà è ðàññ÷èòàííàÿ â òàáëèöàõ 4.6 è 4.7 ïðè óñ-

ëîâèè, ÷òî DT

NET

=0,1° íåçàâèñèìî îò îáëàñòè ñïåêòðà. Íóæíî îòìåòèòü,

÷òî â îáëàñòè ñïåêòðà 812 ìêì ýòà ñîñòàâëÿþùàÿ ïîãðåøíîñòè ïðè

ðàâíûõ êîýôôèöèåíòàõ èçëó÷åíèÿ îáúåêòîâ ñóùåñòâåííî ìåíüøå ïî-

ãðåøíîñòè èçìåðåíèé â îáëàñòè ñïåêòðà 3,55,5 ìêì. Ïðè íèçêèõ çèì-

íèõ òåìïåðàòóðàõ ðàçíèöà â ïîãðåøíîñòè èçìåðåíèé äîñòèãàåò 2-õ

ðàç. Ýòî ïðåèìóùåñòâî äëèííîâîëíîâîé îáëàñòè, îäíî èç îñíîâíûõ

ïðè òåðìîãðàôè÷åñêèõ èçìåðåíèÿõ, ìîæåò áûòü ïðåîäîëåíî òîëüêî

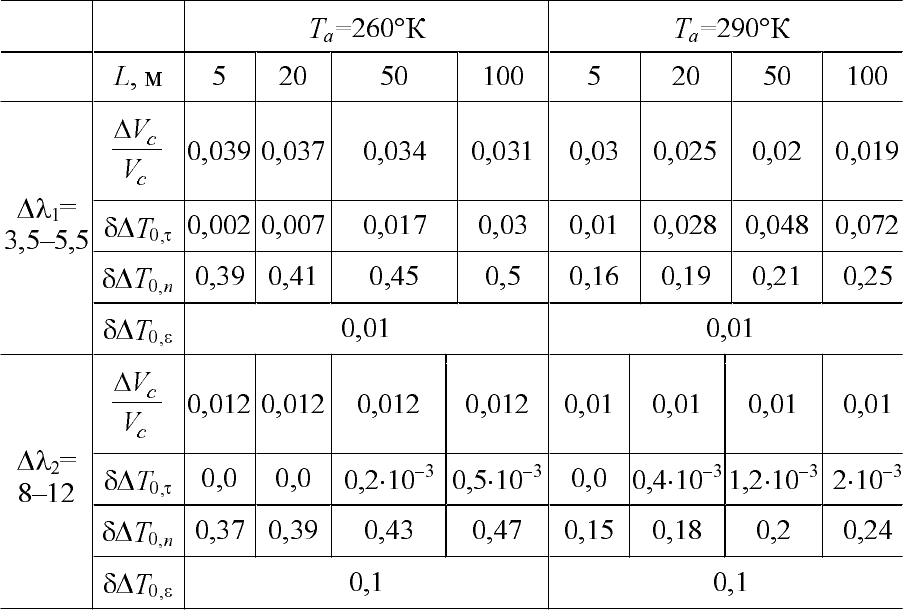
Òàáëèöà 4.7.

Îòíîñèòåëüíûé êîíòðàñò ñèãíàëà è ïîãðåøíîñòè èçìåðåíèé êîíòðàñ-

òà òåðìîäèíàìè÷åñêîé òåìïåðàòóðû DÒ

=1° íåãëàçóðèðîâàííîãî

ôàðôîðà, e

=0,9 , e

» 0,5