AckermannTh. (ed) Wind Power in Power Systems

Подождите немного. Документ загружается.

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 661 – [653–676/24]

17.12.2004 10:52PM

I have used the model of the SVC unit that was developed and implemented as a user-

written model in the simulation tool PSS/E

at the Danish co mpany NESA in

cooperation with the manufacturer ABB Power Systems (Noroozian, Knudsen and

Bruntt, 1999). NESA kindly permitted use of the SVC model.

29.3.1 Wind turbine parameters

The demand for dynamic reactive compensation is dependent on the parameters of

fixed-speed wind turbines, which are both the induction generator parameters and the

mechanical system parameters. In Akhmatov et al. (2003) my colleagues and I showe d

that demands for dynamic reactive compensation can be significantly reduced if:

stator resistance, stator reactance, magnetising reactance and rotor reactance are reduced;

rotor resistance is increased (however, this will also increase power losses in the rotor

circuit during normal operation);

mechanical construction is reinforced in terms of increasing turbine rotor inertia and

increasing shaft stiffness.

By reducing the demand for dynamic reactive compensation one improves short-term

voltage s tability and the ride-through capability. Table 29.2 illustrates the effect of reinfor-

cing the wind turbine’s mechanical construction in order to reduce the demand for dynamic

reactive compensation. The generator and shaft system data show that the only reasonable

comparison is that for different Type A wind turbines. Therefore, an analysis of short-term

voltage stability could be started by comparing such data for Type A wind turbines

produced by different manufacturers. The controllability of Type A wind turbines also

has to be taken into account.

29.3.2 Stabilisation through power ramp

According to Danish specifications (Eltra, 2000), large wind farms have to be able to

reduce their power supply on request. The power may have to be reduced from any

Table 29.2 Mechanical construction in relation to the static VAR compensation (SVC) unit

capacity needed for voltage reestablishment.

Mechanical construction parameter Capacity of SVC unit (MVAR)

Turbine rotor inertia (s) Shaft stiffness (p.u./el.rad)

2.5 0.30 100

2.5 0.15 125

2.5 0.60 50

4.5 0.30 50

Default case.

Source: Akhmatov et al., 2003a. From Electrical Power and Energy Systems, volume 25, issue 1,

V. Akhmatov, H. Knudsen, A. H. Nielsen, J. K. Pederson and N. K. Poulsen, ‘Modelling and

Wind Power in Power Systems 661

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 662 – [653–676/24]

17.12.2004 10:52PM

operational point to an operational point of less than 20 % of rated power in less than

2 s. This procedure is called power ramping. It has been demonstrated that a power

ramp can stabilise large wind farms at a short-circuit fault (Akhmatov, 2001). The

power ramp can effectively be achieved by using the active-stall control of fixed-speed

wind turbines (Akhmatov et al., 2001). In the case of Type A wind turbines, excessive

overspeeding of the wind turbines initiates voltage instability (Akhmatov, 2001). Power

ramp operation means that the wind turbines are decelerated during a grid fault, and in

this way excessive overspeeding is prevented. An external system gives an external signal

that requests a power ramp. The signal is given when abnormal operation at the

connection point of the wind farm is registered, such as a sudd en voltage drop.

There is a delay between the moment the grid fault occurs and the moment the

external signal is given to the wind farm. This delay is about 200–300 ms (Akhmatov

et al., 2003). This means that the request comes only after the grid fault is cleared.

Before the power ramp is requested, the wind turbines are controlled by the regular

control systems of active stall (i.e. by the power optimisation algorithm). If the external

signal requests the power ramp, the regular control systems are switched off and replaced

by the control strategy of the power ramp. This means that the reference blade angle of

each wind turbine in the farm is set to the predefined value corresponding to an output

power of 20 % of rated power (Akhmatov et al., 2003). The reference blade angle during

the power ramp is computed based on the incoming wind and the rotational speed of the

wind turbine rotor. Using the blade servo, the reference value of the blade angle will be

reached. However, there are restrictions on the pitching rate (see Section 27.3.3).

Figure 29.4 shows the computed behaviour of a modern 2 MW wind turbine using the

power ramp during a grid fault. The curves correspond to selected wind turbines in large

wind farms. It can be seen that the mechanical power can be reduced from rated

operation to 20 % of rated operation in less than 2 s. Operation with reduced power

output lasts only a few seconds. This is necessary to prevent fatal overspeeding and it

contributes to volta ge reestablishment after a grid fault and to the fault ride through

capability of the wind farm. In this particular case, the voltage in the power system is

reestablished without use of dynamic reactive compensation (i.e. it is reestablished only

through the power ramp achieve d by active-stall control) and the wind turbines ride

through the fault.

When the power ramp mode is cancelled, the regular control system of active stall is

restarted and becomes operational. The power output will be optimised according to the

incoming wind and the rotational speed of the turbi ne rotor.

If the grid fault is cleared by tripping a number of transmission lines, the short-circuit

capacity of the transmission network is changed. The voltage does not reestablish itself

to the same level as before the grid fault. The rotational speed will also be slightly

different from the value dur ing prefault operation. The result is that the operational

conditions of the wind turbine rotors differ slightly from the those during prefault

conditions. It is argued here that the blade angles of individual wind turbines will not

necessarily be reestablished to the positions prior to the grid fault. The regular control

systems of active stall will find other optimised blade-angle posit ions to reach the

desired power outputs. The curves in Figure 29.5 illustrate this. If the power ramp is

used to stabilise a large wind farm, this will not trigger interaction between the wind

turbines. The simulation results show that the wind turbines will show a coherent

662 Aggregated Modelling and Short-term Voltage Stability

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 663 – [653–676/24]

17.12.2004 10:52PM

response during the grid disturbance. Once the operation of the wind farm is reestab-

lished, there are no further fluctuations of voltage or elect ric power.

In general, use of blade-angle control to stabili se large wind farms equipped with

Type A wind turbines is a useful tool for maintaining transient voltage stability

(Akhmatov et al., 2003). The Danish offshore wind farm at Rødsand applies a similar

technical solution. The rated power of the Rødsand offshore wind farm is 165 MW, and

the farm was taken into operation in 2003. The Rødsand offshore wind farm comprises

72 Type A2 wind turbines from the manufacturer Bonus Energy.

29.4 Wind Turbines with Variable Rotor Resistance

The feature of variable rotor resistance (VRR) is designed as follows: the converter is

connected to the rotor circuit of an induction generator through the slip rings. The

operation of the converter means that an external resistance is added to the impedance

of the rotor circuit. For an analysis of voltage stability, this is reflected in a simplified

representation of the converter control as a dynamically controlled external rotor

–2

–3

–4

–5

–6

–7

–8

–9

–10

–11

0.0 0.5 2.5 3.5

Time (s)

WT 10

WT 50

WT 60

WT 70

WT 80

WT 10

WT 50

WT 60

WT 70

WT 80

(a)

(c)

(d)

(b)

1.0 1.5 2.0 3.0 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0

0.0 0.5 2.5 3.5

Time (s)

1.0 1.5 2.0 3.0 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0

0.0 0.5 2.5 3.5

Time (s)

1.0 1.5 2.0 3.0 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0

0.0 0.5 2.5 3.5

Time (s)

1.0 1.5 2.0 3.0 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0

1.2

1.0

0.8

0.6

0.4

0.2

0.0

3.0

2.5

2.0

1.5

1.0

0.0

–0.5

2.4

2.0

1.6

1.2

0.8

0.4

0.0

Mechanical power (MW)

Electrical power (MW)

Voltage (p.u.)

Blade angle (degrees)

0.5

Figure 29.4 Response of a large wind farm to a short-circuit fault, with use of a power ramp:

(a) blade angle of a selected wind turbine, (b) mechanical power of a selected wind turbine, (c)

voltage and (d) electric power of selected wind turbines. Voltage is reestablished without using

dynamic reactive compensation. Note: for the layout of wind turbines WT 01–WT 80, see Figure

29.1 Reprinted from Electrical Power and Energy Systems, volume 25, issue 1, V. Akhmatov,

H. Knudsen, A. H. Nielsen, J. K. Pederson and N. K. Poulsen, ‘Modelling and Transient Stability

Wind Power in Power Systems 663

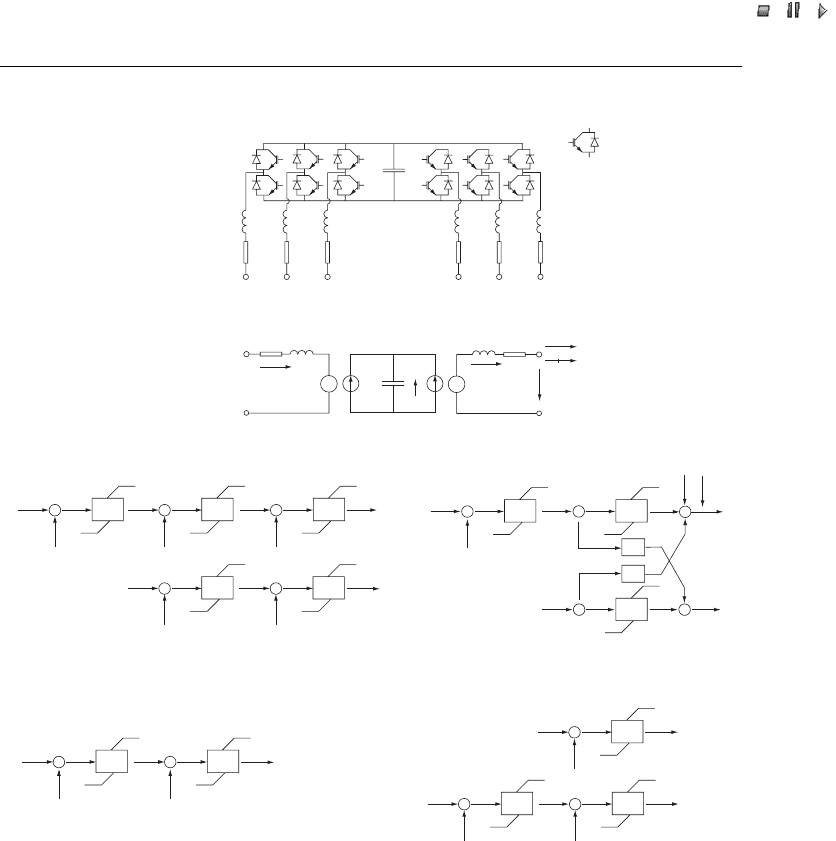
//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 664 – [653–676/24]

17.12.2004 10:52PM

Generator (PMG)/

Rotor (DFIG) converter

Generator (PMG)/

Rotor (DFIG) converter

Grid-side converter

Grid-side

converter

IGBT switch

Smoothing inductorSmoothing inductor

Smoothing inductor

To power network

DC link

To generator

= E

1α

+jE

1β

= |E

|∠ϕ

= U

2α

= I

2α

+jI

2β

= E

2α

+jE

2β

PI PI

= I

1α

+jI

1β

G, Ref

2α, Ref

2, Ref

2α

1α, Ref

1β, Ref

2β, Ref

1β

1α

(a)

(b)

(c)

(e)

PI PI

G, Ref

(f)

–X

2α, Ref

2β, Ref

2β

2α

DC, Ref

(d)

Figure 29.5 Frequency converter and its control system in voltage stability investigations: (a) the

main components and integrated gate bipolar transistor (IGBT) switches, (b) generic electric

scheme, (c) generic control of rotor converter of the doubly fed induction generator (DFIG),

(d) generic control of the grid-side converter, (e) supplementary control of reactive power from the

grid-side converter, and (f) generic control of the generator converter of the permanent magnet

generator (PMG). Note:PI¼proportional–integral controller; c ¼...; E

¼voltage source of DFIG

rotor converter on PMG converter; |E

| ¼magnitude of E

; E

1

¼ active component of E

;

1

¼ reactive component of E

; E

¼voltage source of grid-side converter;

2

¼ active component of E

; E

2

¼ reactive component of E

; I

¼rotor current of DFIG or

generator current of PMG; I

1

¼ active component of I

; I

1

¼ reactive component of I

;

1,Ref

¼ desired value of I

1

; I

1,Ref

¼ desired value of I

1

; I

¼current of grid-side converter;

2

¼ active component of I

; I

2

¼ reactive component of I

; I

2,Ref

¼ desired value of I

2

;

2,Ref

¼ desired value of I

2

; J

¼charging DC current; J

¼discharging DC current;

664 Aggregated Modelling and Short-term Voltage Stability

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 665 – [653–676/24]

17.12.2004 10:52PM

resistance, VRR. In Akhmatov et al. (2003) my colleagues and I describe the model of

Type B wind turbines with a generic control system of VRR with a proportional integral

(PI) controller. The rotor current magnitude controls the value of the external resis-

tance.

The VRR feature is commonly applied in combinat ion with pitch control in order to

reduce flicker (i.e. to improve power quality). In Akhmatov et al. (2003) we demon-

strated that this feature can also be used to improve short-term voltage stability. We also

included the results of an analysis of short-term voltage stability carried out with a wind

farm model with 80 Type B wind turbines. Grid fault s did not trigger any mutual

oscillations between the Type B wind turbines, and the electric and mechanical par-

ameters of the wind turbines show a coherent response.

Use of VRR means that the demand for dynamic reactive compensation in order to

reestablish voltage can be reduced significantly. Furthermore, if pitch control is applied

to prevent excessive overspeeding of wind turbines during grid faults, this will also

contribute to improved short-term voltage stability and the fault-ride-through capability.

VRR (i.e. the converters) cannot be used to control reactive power or cover the static

reactive demands of the induction generators because the converter is applied together

with induction generators that absorb reactive power from the power grid; it is not

designed to control the excitation of such generators. During transient events in the

electric power networks converter protection also has to be taken into account. The

converters may, for example, block during excessive machine current transients

(Akhmatov, 2003a).

Note: the results presented in this section have been discussed with the Danish

manufacturer Vestas Wind Systems, which produces the Opti-Slip

wind turbines.

29.5 Variable-speed Wind Turbines with Doubly-fed Induction Generators

I now wish to present the simulation results for 80 variable-speed wind turbines

equipped with DFIGs. Partial-load frequency converters use the integrated gate bipolar

transistor (IGBT) switches to control the DFIGs. Figure 29.5 shows schematically the

Figure 29.5 (continued) P

¼electric power of grid-side converter; P

¼generator electric

power; P

G, Ref

¼desired value of P

; Q

¼reactive power of grid-side converter; Q

2, Ref

¼desired

esired value of Q

; Q

¼generator reactive power; Q

G, Ref

¼desired value of Q

; R

¼resistance

of smoothing inductor; U

¼terminal voltage; U

2

¼magnitude of terminal voltage;

2,Ref

¼ desired value of U

2

; U

¼DC link voltage; U

DC,Ref

¼desired value of U

;

¼reactance of smoothing inductor; ’

¼ phase angle; !

¼ generator rotor speed;

G, Ref

¼ desired value of !

; Parts (c)–(e) reprinted from Wind Engineering, volume 27, issue 2,

V. Akhmatov, ‘Variable-speed Wind Turbines with Doubly-fed Induction Generators, Part III:

Multi-Science Publishing Co. Ltd, Part (f) reprinted from Wind Engineering, volume 27, issue 6,

V. Akhmatov, A. H. Nielsen, J. K. Pedersen and O. Nymann, ‘Variable-speed Wind Turbines with

Multi-preSynchronous Permanent Magnet Generators and Frequency Converters, Part I:

multi-science Publishing Co. Ltd

Wind Power in Power Systems 665

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 666 – [653–676/24]

17.12.2004 10:52PM

converter and its control. In Akhmatov (2002) I provide the modelling details regarding

the DFIG, shaft system, turbine rotor and generic pitch-control system. In Akhmatov

(2003b) I explain the generic model of the partial-load frequency converter and its

control systems applied in the analysis of voltage stability. It is, however, necessary to

present briefly the converter model in order to understand better the results presented in

this section.

The accuracy of the simulation results depends on a variety of factors. One is the

representation of the partial-load frequency converter and its control. Several studies on

the analysis of voltage stability (Pena et al., 2000; Røstøen, Undeland and Gjengedal,

2002) assume that the rotor converter representation is sufficient for such an analysis

and therefore they neglect the grid-side converter. The reason is that the grid-side

converter has a small power capacity, and it is assumed that this converter can always

follow its references, such as DC link voltage and reactive current.

Unless the terminal voltage changes significantly, this assumption is correct. How-

ever, if there is a significant voltage drop during a short-circuit fault, the grid-side

converter is not able to follow its references (Akhmatov, 2003b). If one neglects the

converter one introduces inaccuracy with respect to the converter’s response during grid

disturbances.

First, this inaccuracy shows when the predictions of transients of the machine current

are excessively high (Akhmatov, 2003b). This is unacceptable, because, basically, the

rotor converter blocks in order to protect against overcurrents (Akhmatov, 2002). This

means that the oversimplified converter model may predict a too frequent blocking of

the converters.

Second, the transient behaviour of the DC link voltage is not available if the grid-side

converter is neglected. When the grid voltage drops, the grid-side converter cannot

supply elect ric power and the DC link voltage starts to fluctuate (Akhmatov, 2003b).

The converter’s protective system monitors the DC link voltage and orders the converter

to block if the DC voltage exceeds a given range.

Third, the damping characteristics of the torsional oscillations excited in the shaft

system may be predicted incorrectly when one applies the oversimplified converter

representation (Akhmatov, 2003a). This may result in misleading conclusions with

respect to the intensity of shaft oscillations and the predicted load on the shaft gear.

It is also important to mention that the grid-side converter can be set to control reactive

power. Through its restricted power capacity, this reactive power control may have an

effect on the voltage recovery rate and may contribute to the successive converter restart,

if the rotor converter has been blocked during the grid fault (Akhmatov, 2003a). This

important behaviour is omitted if the grid-side converter is neglected in the model.

Details regarding the complexity of the converter models in the case of DFIGs and their

partial-load converters were discussed with the manufacturer Vestas Wind Systems, which

produces the Opti-Speed

wind turbines. Vestas Wind Systems agreed that an analysis

of short-term voltage stability should also include a converter model with representations

of the grid-side converter and the DC link rather than only of the rotor converter. It is

necessary to predict with sufficient accuracy the electric parameters that have an effect on

the converter blocking (and restart) during transient events in the power grid.

Vestas Wind Systems kindly provided support regarding the tuning of the parameters

of the generic model of a partial-load frequency converter and its control system.

666 Aggregated Modelling and Short-term Voltage Stability

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 667 – [653–676/24]

17.12.2004 10:52PM

Consequently, the con verters of all the wind turbines in the farm are modelled with

representation of the rotor converters as well as the grid-side converters and their

respective control systems, in order to reach a higher accuracy. Figures 29.5(c) and

29.5(d) give the generic control systems of the rotor and the grid-side converters of the

DFIG. The rotor converter controls the generator in a synchronously rotating

(, )-reference frame with the -axis oriented along the terminal voltage vector. Using

this control, the electric and reactive power of the DFIG are controlled independent of

each other (Yamamoto and Motoyoshi, 1991).

The grid-side converter control is similar to that of a Statcom (Akhmatov, 2003a;

Schauder and Mehta, 1999). The grid-side converter is controlled in the same reference

frame as the rotor converter (Akhmatov, 2003b). The grid-side converter control is designed

with independent control of the DC link voltage and the reactive current. Voltage compen-

sation is achieved by cross-coupling. The switching dynamics in both converters is

neglected, since the rotor converter and the grid-side converter are able to follow their

respective reference values for the induced voltage sources at any time (Akhmatov, 2003b).

Figure 29.6(e) shows the supplementary system to control reactive power from the

grid-side converter. Here, control coordination between the rotor and the grid-side

converters is necessa ry (Akhmatov, 2003b).

29.5.1 Blocking and restart of converter

The wind turbines have to operate without interruption during grid faults that is the

fault-ride-through. During such an event, the voltage drops. This causes transients in the

machine and the grid-side converter currents. There are also fluctuations in the DC link

voltage (Akhmatov, 2003b). The converter’s protective system monitors currents in the

rotor circuit and the grid-side converter, the DC link voltage, the terminal voltage, the

grid frequency and so on. The converter will block if one or more monitored values

exceed their respective relay settings. The characteristic blocking time is in the range of a

few milliseconds (Akhmatov, 2002). The rotor converter stops switching and trips. The

converter blocking may lead to disconnection of the wind turbine (Akhmatov, 2002).

In Akhmatov (2002) I suggest a feature to maint ain the ride-through capability with a

fast restart of the converter after the fault. This feature was then validated by simula-

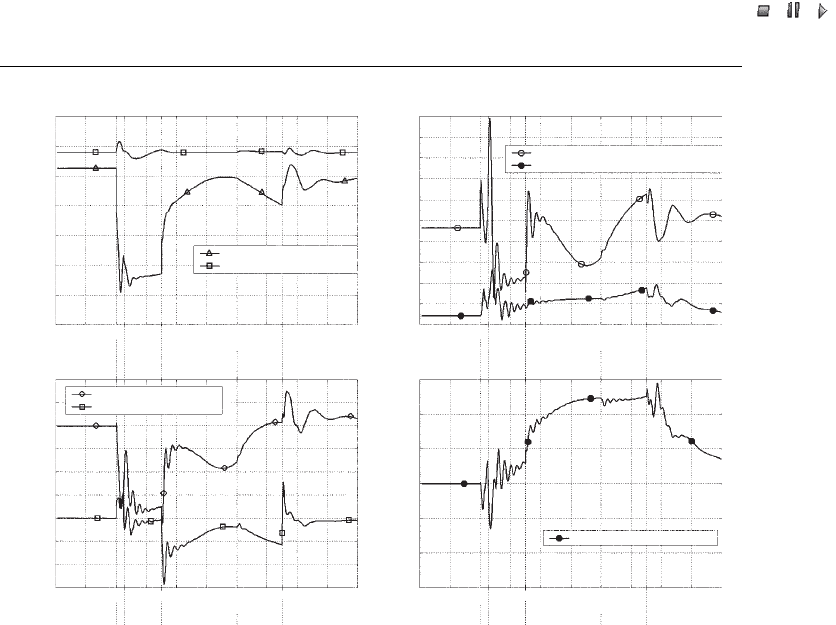
tions (Akhmatov, 2003a). The simulated curves shown in Figure 29.6 illustrate the fault-

ride-through capability with a fast restart of the converter. The curves correspond to

wind turbine WTG 01. From the start of the simulation to tim e t ¼T

, the power system

is in normal operation. At time T

, the transmission power network is subjected to a

short-circuit fault.

At time t ¼T

, the rotor converter blocks by overcurrent (transients) in the rotor

circuit. The rotor circuit is short-circuited through an external resistor (Akhmatov,

2002). When the rotor converter blocks, the wind turbine operates as a Type A1 wind

turbine with an increased rotor resistance. Pitch control protects against excessive

overspeeding of the wind turbine, as explained in Se ction 29.3.2. The grid-side converter

operates as a Statcom, controlling DC link voltage and reactive power. This contributes

to a faster reestablishment of the terminal voltage. This controllability is, however,

restricted by the power capacity of the grid-side converter.

Wind Power in Power Systems 667

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 668 – [653–676/24]

17.12.2004 10:52PM

The grid fault is cleared at time t ¼T

. Once the voltage and grid frequency are

reestablished within their respective ranges, the rotor converter synchronisation is

started. The IGBT of the rotor converter starts switching and the external resistance is

disrupted from the rotor circuit. During synchronisation, the rotor co nverter prepares

to restart. Synchronisation begins at time t ¼T

and protects the rotor converter against

blocking during the restart sequence, which could be caused by excessive transients in

the rotor current or unacceptably large fluctuations of the DC link voltage.

At time t ¼T

, the rotor converter has restarted. Shortly after, normal operation of

the wind turbine is reestablished. The feature with a fast restart of the rotor converter is

designed for a ride-through operation of wind turbines in a large wind farm during grid

disturbances.

29.5.2 Response of a large wind farm

One of the main concerns regarding wind farms is the risk of mutual interaction between

the converter control systems of a large number of Type C wind turbines. Such concerns

1.4

1.2

1.0

0.8

0.6

0.4

0.2

0.0

1.4

1.6

1.8

2.0

1.2

1.0

0.8

0.6

0.4

0.2

0.0

0.6

0.4

0.2

0.0

–0.2

–0.4

–0.6

2.0

2.5

3.0

1.5

1.0

0.5

0.0

–0.5

–1.0

–1.5

0.3

(a) (b)

(d)(c)

0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3

Voltage (p.u.)

Current (p.u.)

Time (s)

0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3

Time (s)

0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3

Time (s)

0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3

Time (s)

WT 01: Terminal voltage

WT 01: Rotor current

WT 01: Gride-side converter current

WT 01: Gride-side converter

WT 01: DC link voltage

WT 01: Electric power

Electric power (MW), Reactive power (MVAR)

WT 01: Reactive power

Reactive power (MVAR)

Figure 29.6 Uninterrupted operation feature with fast restart of the rotor converter: (a) terminal and

DC link voltages, (b) rotor and grid-side converter current, (c) electric and reactive power, and (d)

reactive power of grid-side converter. Reprinted from Akhmatov, V., Analysis of Dynamic Behaviour

of Electric Power Systems with Large Amount of Wind Power, Ph.D dissertation, Technical University

668 Aggregated Modelling and Short-term Voltage Stability

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 669 – [653–676/24]

17.12.2004 10:52PM

are reinforced during the following situations: (a) fast-acting partial-load frequency

converters of the DFIG and (b) when the rotor converters of many wind turbines

execute blocking and restarting sequences during a short time interval at a grid

fault. Voltage stability is maintained without dynamic reactive compensation. The

grid-side converters of the DFIG will control reactive power and voltage during the

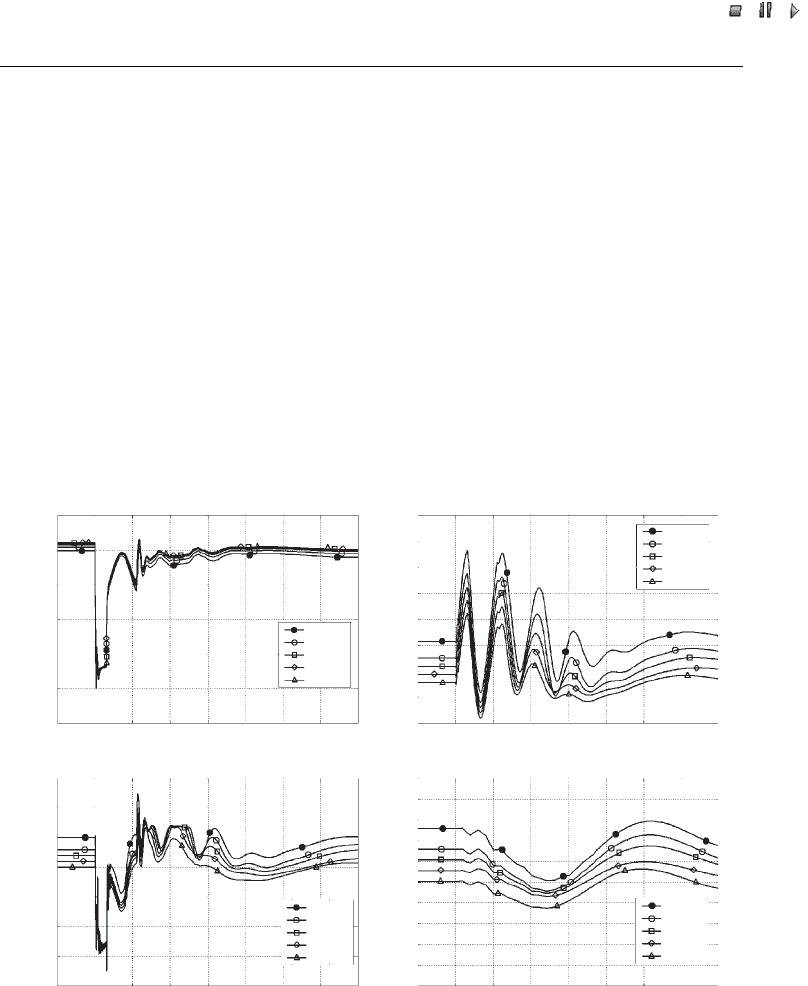
transient event (Akhmatov, 2003a). Figure 29.7 includes the simulated curves for

the selected wind turbines operating at different operational points. The simulation

results do not indicate any risk of mutual interaction between the converters of the

different wind turbines. The Type C wind turbines show a coherent response during

the grid fault.

Properly tuned converters are not expected to cause mutual interaction between

wind turbines in large wind farms (Akhmatov, 2003a). This result is, however, based

on the given control strategy of the variable-speed wind turbines and the given power

network.

1.2 0.2

0.18

0.16

0.14

0.12

0.1

0.08

0.06

0.04

1.0

0.8

0.6

0.4

0.2

0.0

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0

Time (s)

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0

Time (s)

Voltage (p.u.)

Speed deviation (p.u.)

WT 10

WT 50

WT 60

WT 70

WT 80

WT 10

WT 50

WT 60

WT 70

WT 80

WT 10

WT 50

WT 60

WT 70

WT 80

WT 10

WT 50

WT 60

WT 70

WT 80

3.0

2.5

2.0

1.5

1.0

0.5

0.0

–0.5

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0

2.5

2.3

2.1

1.9

1.7

1.5

1.3

1.1

0.9

0.7

0.5

Electric power (MW)

Mechanical power (MW)

(a)

(c)

(b)

(d)

Figure 29.7 Response of a large wind farm with doubly fed induction generators (DFIGs) to a

short-circuit fault using: (a) terminal voltage, (b) generator rotor speed, (c) electric power, and

(d) mechanical power (illustration of pitching) of selected wind turbines; voltage is reestablished

without dynamic reactive compensation. Note: For the layout of wind turbines WT 01–WT 80, see

Figure 29.1. Reprinted from Akhmatov, V., Analysis of Dynamic Behaviour of Electric Power

Systems with Large Amount of Wind Power, Ph.D dissertation, Technical University of Den-

Wind Power in Power Systems 669

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 30_CHA29 .3D – 670 – [653–676/24]

17.12.2004 10:52PM

29.6 Variable-speed Wind Turbines with Permanent Magnet Generators

In this Section I present the simulation results based on 80 variable-speed wind turbines

equipped with PMG and frequency converters. Table 29.3 shows the data for the wind

turbine. This wind turbine type has no gearbox and therefore the generat or is direct-

driven by the wind turbine through the low-speed shaft (Grauers, 1996). The generator

has a large number of poles and a relatively large value of reactance (Spooner, Williamson

and Catto, 1996).

The generator consists of two sections of slightly above 1 MW placed on one rotor

shaft. Figures 29.5(d)–29.5(f) illustrate the generi c control system of the frequency

converter. The generic control system of the grid-side converter is similar to the control

system applied in the case of a DFIG. The PMG is controlled by the generator

converter, where the electric power is controlled by the phase angle, and its reactive

power (kept reactive-neutral) is controlled by the voltage magnitude.

Again, the main concern is to achieve a ride-through operation of the Type D wind

turbines with PMGs. The protective system of the frequency converter monitors the

machine current, the current in the grid-side converter, the DC link voltage, the terminal

voltage, the grid frequency and so on; the converter will block if one or more of the

monitored parameters exceed their relay settings. This may lead to disconnection and

stopping of the wind turbine. In the case of a PMG, the machine current magnitude is

also among the critical parameters be cause an excessive machine current may demag-

netise the permanent magnets.

These concerns have to be taken into account when presenting a ride-through feature

with blocking and fast restart of the converter during a grid fault. Figure 29.8 shows the

dynamic behaviour of Type D wind turbines with PMGs. The short- circuit fault occurs

at time t ¼T

. At time t ¼T

, the converter’s protective system registers an abnormal

operation and requests a blocking of the generator converter. The IGBT switches stop

switching and open. Then the DC link capacitor will be charged through the diode

Table 29.3 Data for a 2 MW wind turbine equipped with a permanent magnet generator (PMG)

Generator Value Grid-side converter Value

Rated power (MW) 1.01 2 Rated power (MW) 2

No-load voltage (p.u.) 1.40

Rated voltage (p.u.) 1.0

Rotational speed (rpm) 10.5–24.5 Rated frequency (Hz) 50

Number of poles 64 Rated DC link voltage 1.16

Lumped inertia (s) 4.8 DC link capacitor (p.u.) 0.1

Resistance (p.u.) 0.042 Mains resistance (p.u.) 0.014

Reactance X

(p.u.)/X

(p.u.) 1.05/0.75 Mains reactance (p.u.) 0.175

966 V.

690 V.

800 V.

Source: Akhmatov et al ., 2003. From Wind Engineering, volume 27, issue 6, V. Akhmatov,

A. H. Nielsen, J. K. Pedersen and O. Nymann, ‘Variable-speed wind turbines with multi-pole

synchronous permanent magnet generators. Part 1: Modelling in dynamic simulation tools’,

670 Aggregated Modelling and Short-term Voltage Stability