AckermannTh. (ed) Wind Power in Power Systems
Подождите немного. Документ загружается.

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 531 – [523–554/32]
17.12.2004 10:48PM
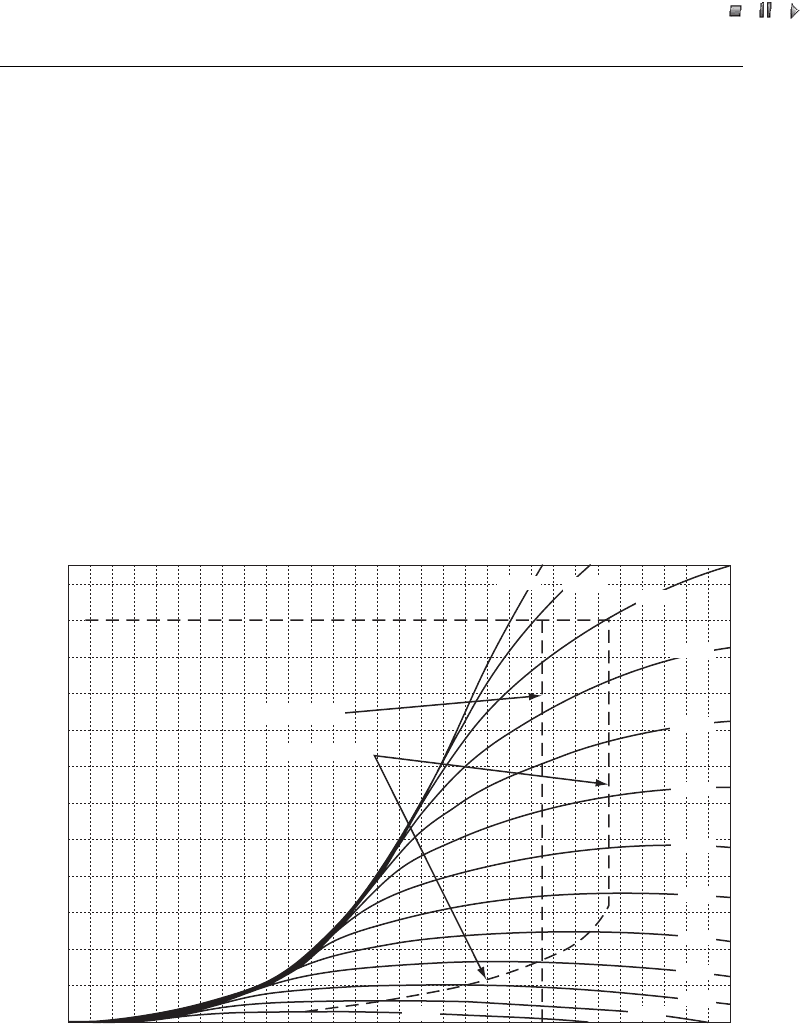
Figure 24.3 gives an example that illustrates the mechanical power from a fixed-speed
and a full variable-speed wind turbine. It shows that the mechanical power output is
higher for the variable-speed wind turbine at all wind speeds. Only at a wind speed of
7 m/s, is the mechanical power output the same.
Other things being equal, variable-speed wind turbines will yield greater annual power
production compared with similar fixed-speed wind turbines. This improvement in
efficiency is, however, obtained at the cost of greater complexity in the construction
of the unit and also some additional losses in the power electronic converters, which
enable the variable-speed operation (for more details, see Chapt er 4). If the wind turbine
is erected in an environment with high winds (e.g. offshore) the gain in annual energy
production may be less significant, because this gain is achieved primarily in low-wind
situations. Also, if the speed controllability is achieve d at the cost of additional losses
(e.g. in frequency converters) the net result might even be negative. Some fixed-speed
wind turbines can, in a way, even be characterised as variable-speed wind turbines, or at
least as two-speed wind turbi nes. Some manufacturers either include two generators – a
high-power and a low-power generator – with a different number of pole pairs, into the
wind turbine, or they apply a special generator, which is able to change the number of
0
200
400
600
800
1000
1200
1400
1600
1800
2000
2200
2400
16 m/s
15 m/s
14 m/s
13 m/s
12 m/s
11 m/s
10 m/s
11 m/s
9 m/s
8 m/s
7 m/s
6 m/s
5 m/s
4 m/s
Fixed-speed
Variable-speed
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Rotational speed (rpm)
Mechanical power (kW)
Figure 24.3 Illustrative mechanical power curves of fixed-speed and variable-speed wind turbines
for various wind speeds (4–16 m/s). Reproduced from Wind Engineering, volume 26, issue 2,
V. Akhmatov, ‘Variable Speed Wind Turbines with Doubly-fed Induction generators, Part I:
Modelling in Dynamic Simulation Tools’, pp. 85–107, 2002, by permission of Multi – Science
Publishing Co. Ltd
Wind Power in Power Systems 531

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 532 – [523–554/32]
17.12.2004 10:48PM
pole pairs (e.g. from 2 to 3) by changing the connections of the stator windings. In this
way, a certain fraction of the increase in annual power production from a variable-speed
turbine is obtained through a very simple and cost-effective measure.
At high wind speeds, the mechanical power with the optimal C
P
value will exceed the
nominal power for which the wind turbine is designed. It is therefore necessary to reduce
the mechanical power. This is achieved by turning the blades away from the optimal
pitch angle. There are two possibilities for doing this – either out of the wind or up
against the wind:
.
If the blades are turned out of the wind, the lift on the blades is gradually reduced.
This is called pitch control and requires a relatively large change in pitch angle to
reduce power significantly.
.
If the blades are turned up agains t the wind, the turbine blades will stall and thus
automatically reduce the lift on the turbine blades. This effect is obtained with a
relatively small change in pitch angle. This is called active stall control and requires a
more accurate control of the pitch angle because of the high angular sensitivity.
24.3.2 Different representations of the turbine rotor
After having described the basic aerodynamic properties of the wind turbine, we can
now present the most commonly applied different ways of representing a wind turbine in
simulation programs. The various model representations are most conveniently
approached by first stating whether the representation is based on power, P, torque, T,
or the power efficiency coefficient, C
P
. It is beyond the scope of this general overview to
go into the details of the various modelling approaches. In the following, we will only
outline the major aspects in order to provide a general overview.
24.3.2.1 Constant power
The simplest possible representation of a wind turbine is to assume a constant mechanical
input. The mechanical input can be chosen as either the mechanical power or the mechan-
ical torque, and then the other quantity can be calculated by using Equation (24.3).
Even though both ways are possible, we strongly recommend the constant power
representation. If constant torque is applied, the mechanical power in the model will
vary proportionally with the rotational speed. In certain cases, this may result in a
numerically unstable model system. In contrast, in a constant power representation the
torque is an inverse function of the rotational speed and thus introduces an intrinsically
stabilising term into the mechanical system. More importantly, a constant torque model
will in most cases reflect the physical behaviour of the wind turbine less a ccurately than
a constant power model.
24.3.2.2 Functions and polynomial approximations
Functions and polynomial approximations are a way of obtainin g a relatively accurate
representation of a wind turbine, using only a few parameters as input data to the
532 The Modelling of Wind Turbines

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 533 – [523–554/32]
17.12.2004 10:48PM
turbine model. The different mathematical models may be more or less complex, and
they may involve very different mathematical approaches, but they all must generate
curves with the same fundamental shape as those of the physical wind turbine.
As previously mentioned, the advantage of a C
P
representation is that it is a
normalised representation. For that reason, C
P
representations are convenient
for use in connection with functions and polynomial approximations.
As a simple example of such a function, consider the following polynomial
approximation:
C
P
¼ C
P;max
f1 k
ð
opt
Þ
2
gf1 k
ð
opt
Þ
2
g: ð24:9Þ
This function is characterised by only five parameters: k
, k
,
opt
,
opt
and C
P,max
,
where k
is the tip speed ratio coefficie nt, and k
is the pitch angle coefficient. The
example has never been applied in actual studies and is probably too simple for most
wind turbine simulations. However, the example does fulfil a number of necessary
conditions for a polynomial approximation (such as that a number of selected signifi-
cant points match exactly and that there is a continuity between these points) and
thereby also for achieving a reasonably high accuracy in the vicinity of the desired
working point.
There are other alternatives, of course, which are based on more complicated
approaches, such as higher-order approximations or completely different types of func-
tions. The Fourier expansion with trigonometric functions, for instance, could be a
reasonable way to represent the angular dependency of the turbine blades.
For the most simple wind turbines [i.e. passive-stall, constant-speed wind turbines
(Type A turbines; Section 4.2.3)], the problem is only two-dimensional, since the blade
angle is constant. Therefore, a simple power – wind speed curve will provide the
information that is necessary to determine a C
P
curve. This has been demonstrated
in Akhmatov (1999) .
For more advanced wind turbines with blade angle control (fixed-speed or variable-
speed wind turbines) the problem becomes three-dimensional as the blade angle con-
trollability has to be taken into account. Examples of actually applied functional
approximations are included in Section 25.5.3 and in Slootweg, Polinder and Kling
(2002).
24.3.2.3 Table representation
Instead of applying a functional or polynomial approximation to C
P
it is also possibl e to
apply a more cumbersome but direct approach by simply using a C
P
table. If
the value of C
P
is specified for a number of combinations of and values, the C
P
values can be organised in a matrix. A suitable interpolation method must then be
applied between the nodes in this matrix. The advantage of the table representa-
tion is that it is simple to understand and explain and that the necessary accuracy can be
achieved simply by selecting a suitable resolution of the matrix. The disadvantage is
equally obvious: the tables – and thereby the amount of necessary data – may be rather
substantial.
Wind Power in Power Systems 533

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 534 – [523–554/32]
17.12.2004 10:48PM
24.3.2.4 Blade element momentum method and aeroelastic code
From a physical perspective, the wind pressure yields a force on each blade, which is
turned into a torque on the shaft of the turbine rotor. A torque representation is
therefore, from a physica l perspective, the most natural way to model a turbine rotor.
This model representation is known as the blade element momentum (BE M) method.
This method is used to calculate the C
P
values used in some of the previously mentioned
approaches to represent the turbine rotor; e.g. the table representation in 24.3.2.3.
In short, this method is based on a separation of the blades into a number of sections
along the length of each blade. Each blade section is then characterised by the blade
geometry, and the aerodynamic properties are given for each section from the hub
(r ¼0) to the blade tip (r ¼R) as functions of the local radius r. We can calculate the
static forces on the blade element, and consequently the corresponding shaft torque, for
a given wind speed, V
WIND
, a given rotational speed, !
turb
, of the turbine rotor and a
given blade angle .
Like all the previous representations, this is a static aerodynamic representation. The
BEM method is based on the assumption that the turbine blades at all times are in a
steady-state condition – or at least in a quasi steady-state condition. How ever, it is
possible to represent the aerodynamic transition process during changes of wind speed,
V
WIND
, rotational speed, !
turb
, and/or blade angle, , through some characteristic time
constants. Øye (1986) suggested an engineering model that describes this modification of
the BEM method. The verification of the aerodynamic rotor model in Section 27.2.3
shows the effect of this aerodynamic model representation. The same section also
discusses the use of the static aerodynamic representation and the aerodynamic repre-
sentation including the aerodynamic transition processes.
It is possible to extend the level of detail in the aerodynamic model by taking into
account the flexibility of the blades. In that case, traditional beam theory is used to
model the blades. This method is commonly referred to as an aeroelastic code (AEC).
24.4 Basic Modelling Block Description of Wind Turbines
Modern wind turbines are complex and technically advanced constructions. The wind
turbine models in various simulation programs reflect this complexity. Further, the
wind turbine models in various simulation programs – as well as the models of all other
components – are normally designed to accomm odate specific purposes for which each
simulation program is intended. Therefore, wind turbine models in different simulation
programs may differ substantially and may require very different data, often with widely
varying levels of detail in the various parts of the construction.
However, considering the modelling, wind turbines can in most cases be represented
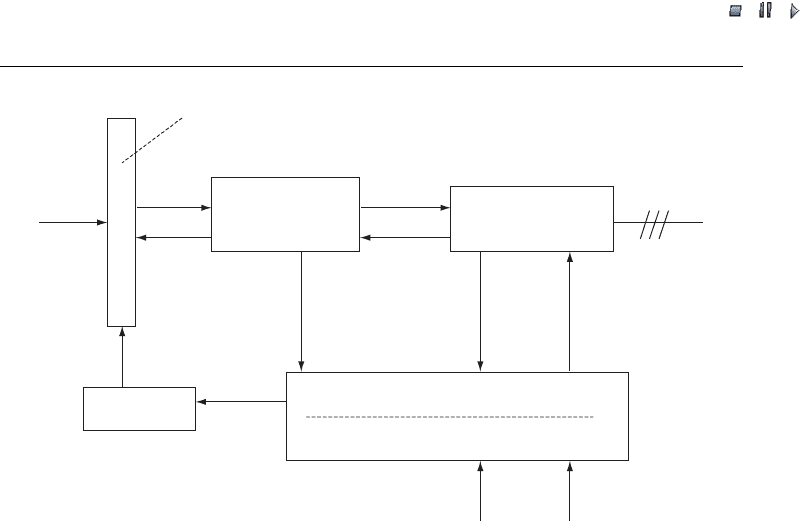
by a generi c model with six basic block elements and their interconnections (see Figure
24.4) or by so mething similar, depending on the specific wind turbine in question. The
six model elements, which will be described in the follo wing six subsections, are the
model representation of the:
.
aerodynamic system;
.
mechanical system (turbine rotor, shafts, gearbox and the generator rotor);
534 The Modelling of Wind Turbines
//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 535 – [523–554/32]
17.12.2004 10:48PM
.
generator drive (generator and power electronic converters, if any);
.
pitch control system;
.
wind turbine control system;
.
protection system of the wind turbine.
For any specific wind turbine model in any simulation program, it should be possible to
identify all model parts with something in the generic model. Likewise, it should also be
possible to associate all data in the model with a physical meaning in this generic mod el.
24.4.1 Aerodynamic system
The aerodynamic system of a wind turbine is the turbine rotor (i.e. the blades of the
wind turbine). The turbine rotor reduces the air speed and at the same time transforms
the absorbed kinetic energy of the air into mechanical power, P
MECH
. A specific wind
turbine rotor is represented by data that describe the constructional design of the
wind turbine. In addition to constructional design data, the mechanical power output of
the turbine depends on the wind speed, V
WIND
, the blade angle, , of the turbine blades,
and the rotational speed, !
turb
, of the turbine rotor. This was described in more detail
in Section 24.3. In this context – that is, in order to provide an overview of the generic
model – it is sufficient to express the mechanical power output of a wind turbine with
P
ref
U
R
Rotor model
Q
ref
and/or U
ref
P, Q,
U
S
, f
NET
I
S
, I
R
ω
turb
ω
turb
, ω
gen
, θ
gen
T
MECH
T
el
Mechanical
shaft model
Generator drive
model
β
β
ref
Pitch servo
ω
gen
, θ
gen
Wind turbine control system
Wind turbine protection system
Wind
Figure 24.4 Block diagram of a generic wind turbine model. Note: f
NET
¼ grid electrical fre-
quency; I
s
¼stator current; I
R
¼rotor current; P ¼active power; P
ref
¼active power reference;
Q ¼reactive power; Q
ref
¼reactive power reference; U
S
¼stator voltage; U
R
¼rotor voltage;
U
ref
¼stator voltage reference T
el
¼ electrical torque; T
MECH
¼Mechanical torque;
!
turb
¼rotational speed of turbine; !
gen
¼ rotational speed of generator rotor;
gen
¼ generator
rotor angle; ¼ pitch angle;
ref
¼ blade reference angle
Wind Power in Power Systems 535

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 536 – [523–554/32]
17.12.2004 10:48PM
specific constr uctional data as a function of rotational speed, wind speed and blade
angle, as in Equation (24.4).
Depending on the modelling environment and on the choices made by the model
developer, the link between the aerodynamic system and the mechanical system will be
either mechanical power, P
MECH
, or mechanical torque, T
MECH
. As previously stated,
they are related to each other by the rotational speed, !
turb
, as shown in Equation (24.3).
24.4.2 Mechanical system
The mechanical system of a wind turbine is the drive train, which consists of the rotating
masses and the connecting shafts, including a possible gear system. The major sources of
inertia in this system lie in the turbine and in the generator rotors. The tooth wheels of
the gearbox contribute only a relatively small fraction. For that reason, the inertia of the
gear is often neglected and only the transformation ratio of the gear system is included.
Thus, the resulting mechanical system model is a two-mass model with a connecting
shaft, and with all inert ia and shaft elements referred to the same side of the gearbox, as
indicated in Figure 24.5. If necessary, it is also possible to include a representation of the
gear system with inertias together with both the low-speed and the high -speed system.
This will result in a system with three rotating masses and two shafts.
The significance of applying a two-mass model of the mechanical shaft system, and
not a lumped mass model is illustrated in the partial verification of the shaft system
model in Section 27.2.2 and in the full-scale model verification in Section 27.3. In wind
turbines, the shaft representation is in general more important, because of the relatively
soft shaft, in comparison with the sh aft systems of traditional power plants. Shafts can
be considered soft when the shaft stiffness is below 1 p.u., when measured in per unit (see
Section 24.5). They are considered stiff when the stiffness exceeds 3 p.u.
24.4.3 Generator drive concepts
In this context, the term generator drive is a broad term covering everything from the
shaft and the main terminals to the power grid. For Type C and Type D wind turbines,
the converters are considered to be an integral part of the generator drive.
(1)
K
tot
H
turb
H
gen
Figure 24.5 Two-mass shaft system model. Note: H
gen
¼inertia of generator; H
turb
¼inertia of
the turbine; k
tot
¼total shaft stiffness
(1)
For definitions of wind turbine Types A–D, see Section 4.2.3.
536 The Modelling of Wind Turbines

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 537 – [523–554/32]
17.12.2004 10:48PM
24.4.3.1 Fixed-speed wind turbines: Types A and B
The generator drive in a fixed-speed wind turbine is only the induction generato r itself.
In the case of a conventional induction generator with a short-circuited rotor (Type A
wind turbine) the rotational speed is limited to a very narrow range, which is determ ined
by the slip of the inducti on generator. Induction machine models are readily available in
most power system simulation programs.
In the case of an induction generator with a variable rotor resistance (Type B wind
turbine) it is possible to vary the speed over a somew hat wider range. However, the
speed range is still rather limited and the speed cannot be controlled directly. Hence,
looking at it from a control system perspective, this type of wind turbine must essentially
be considered as a fixed-speed wind turbine. In addition to the model of the induction
generator itself, a model of a generator drive with an induction generator with variable
rotor resistance has to include a representation of the control system, which determines
the instantaneous value of the rotor resistance. The vast major ity of simulation pro-
grams do not contain such models as standard.
24.4.3.2 Variable-speed wind turbines: Types C and D
As the name indicates, variable-speed generator drives enable the wind turbine control
system to adapt the rotational speed of the wind turbine rotor to the instantaneous wind
speed over a relatively wide speed range. The electrical system has a fixed frequency,
though. A generator drive connecting a variable-speed mechanical system with a fixed-
frequency electrical system must therefore contain some kind of a slip or decoupling
mechanism between the two systems.
In wind turbine technology, the doubly-fed induction generator drive and the full-
load converter connected ge nerator drive are the two most frequently applied variable-
speed generator drive concepts. There are also other variable-speed generator drive
types, but they are currently not generally applied in wind turbines. It would probably
also be possible to use written pole synchronous generators, for instance, as a way of
obtaining variable-speed capability in a generator drive. In short, all types of variable-
speed high-power drives – electrical, mechanical or hydraulic with an electrical generator
somewhere in the drive system – can, theoretically, be applied in wind turbines.
All variable-speed generator drives have one thing in common: they must be able to
control the instantaneous active power output, otherwise it would be impossible to
maintain a power balance in the rotating mechanical system and thus it would also be
impossible to maintain the desired constant rotor speed of the turbine. For most variable-
speed generator drives, such as the presently prevailing Types C and D, for instance, it will
at the same time be possible to control the reactive power output. This implies that the
drive will need externally defined reference values for active and reactive power.
In general, variable-speed generator drives will consist of a more or less traditional
generator combined with power electronics to provide the slip or decoupling mechanism.
As yet, most simulation programs do not include such models as standard. There may
be standard models of the individual components (i.e. the synchronous and induction
generators, and the frequency converters) but they are not integrated into a unified model
with the necessary, additional, internal control systems needed in a variable-speed
Wind Power in Power Systems 537

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 538 – [523–554/32]
17.12.2004 10:48PM
generator drive. Hence, at the moment it is up to the users to implement appropriate
models of variable-speed generator drives. However, the increasing number of wind
turbines using these types of generator drive creates a strong demand for such models. It
is therefore probably only a matter of time before such standard models will be available
in most commercial power system simulation programs.
24.4.3.3 Model implementation: dynamic stability vs. transient generator models
Once a model is developed, the implementation of the model in any simulation program
is, in principle, straightforward, albeit often cumbersome. However, some types of
simulation program contain limitations that make it impossible to implement complete
models in a phy sically correct way. In dynamic stability programs (see Section 24.6.2.2)
the basic algorithms of the program are traditionally based on the assumption that all
electromagnetic transients have been extinguished and that only the electromechanical
transients and the control system transients are present in the network. Therefore, in
order to incorporate a model into a dynamic stability program, it is necessary to make a
number of assumptions (e.g. see Kundur, 1994, pages 169–179 and 300–305).
If the electromagnetic transients are ignored in the model implementation, DC
offsets in the machine stator currents will be neglected. This implies that the time
derivatives of the fluxes in the stator windings are neglected and the stator fluxes are
eliminated as state variables and instead calculated as algebraic variables. Model
implementations of this type are referred to as dynamic stability models, as opposed
to model implementations including the stator fluxes as state variables, which may be
referred to as transient (or full transient) models. These model implementations are
often referred to as third-order and fifth-order models, respectively, where the order
denotes the number of state variables in the generator model. In the third-order model,
the state variables are the rotor speed, and the rotor d -axis and q-axis fluxes. In the
fifth-order models, these state variables are supplemented with the stator d-axis and
q-axis fluxes.
It is, however, possible to incorporate a transient – or at least a semitransient – model
into dynamic stability programs using appropriate ways of getting around the con-
straints in the simulation program. Kundur (1967) describes one way of doing this. It
may be of significance to all generator drives, that include an electrical generator that is
directly grid-connected (i.e. win d turbine Types A–C).
The partial verification of the induction generator model in Section 27.2.1 and the
full-scale model verification in Section 27.3 show the significance of applying a full
transient model as opposed to a dynamic stability model in the case of fixed-speed wind
turbines with induction generators. The significance of the stator fluxes lies in that they
cause a brief braking torque in the case of an external disturbance. In general, a small
and brief braking torque would be of no importance, but in wind turbines the inertia of
the generator rotor is quite small and, at the same time, the shaft system is relatively
soft. The combination of braking torque, low-inertia rotor an d soft shaft causes the
generator rotor to enter the subsequent transient with a slightly slower rotor speed.
Again, a small speed deviation would be insignificant for most other types of generators,
but for induction generators the slip-dependence means that the generator will absorb
538 The Modelling of Wind Turbines

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 539 – [523–554/32]
17.12.2004 10:48PM
more reactive power and generate less active power. Consequently, a small initial speed
difference may lead to a significantly different end result. This phenomenon is illustrated
in the speed cu rves in Figure 27.3.b (page 609) and is also describe d in Knudsen and
Akhmatov (1999) and in Akhmatov and Knudsen (1999b).
Such a verification has not been performed for variable-speed wind turbines, but there
is no doubt that the generator implementation will affect the simulated stator currents
and, consequently, the possible actions of the overcurrent protection systems. The stator
transient itself is probably irrelevant to the overall course of events in a variable-speed
generator drive. However, if the transient itself can cause a protect ive action (see Section
24.4.6) the representation of the trans ients will be significant anyhow.
24.4.4 Pitch servo
In variable-pitch wind turbines, the blade angle is controlled by a pitch servo. The main
control system produces a blade refer ence angle and the pitch servo is the actuator,
which actually turns the turbine blades to the ordered angle.
The pitch servo is subject to constructional limitations, such as angular limits
min
and
max
. That means that the blades can only be turned within certain physical limits. For
active-stall-controlled wind turbines, the permissible range will be between 90
and 0
(or even a few degrees to the positive side), whereas for pitch-controlled wind turbines
the permissible range will lie between 0
and þ90
(or even a few degrees to the negative
side). The control system may impose other, normally narrower, limits on the reference
angle, though.
Likewise, there are limitations on the pitch speed, d/dt. The pitch speed limit is likely
to be higher for pitch-controlled wind turbines than for active-stall-controlled wind
turbines, which have a higher angular sensitivity (see Section 24.3.1). The pitch speed
limit may differ significantly for a positive (d/dt
pos, max
) and negative (d/dt
neg, max
)
turning of the blade. The pitch speed is normally less than 5
per second, although the
pitch speed may exceed 10
per second during emergencies.
24.4.5 Main control system
The exact structure of the main control system is unique for each type of w ind turbine,
and even for the same type of wind turbine it may vary according to the individual
manufacturer. However, the basic tasks of the control system are the same, namely,
to control the power and speed of the wind turbine. The most significant difference
is whether the control system is used in a fixed-speed or in a variable-speed wind
turbine.
24.4.5.1 Fixed-speed wind turbines: Types A and B
For fixed-speed wind turbines, the generator can be considered to be a passive power-
producing component. In effect, the turbine blade angle is the only controllable quantity
in the entire wind turbine. Through measurements of a number of quantities such as
wind speed, turbine rotor speed and active electrical power, the control system optimises
Wind Power in Power Systems 539

//INTEGRAS/KCG/P AGIN ATION/ WILEY /WPS /FINALS_1 4-12- 04/0470855088_ 25_CHA24 .3D – 540 – [523–554/32]
17.12.2004 10:48PM
the blade angle in relation to the incoming wind. In high winds, the control system can
reduce the power from the wind turbine, thus keeping the power at the rated maximum
power of the wind turbine. In emergency situations, the blade angle control can also be
used for preventive rapid power reduction. It can be activated through an external signal
from the grid control centre, for instance, or some other external source, or by a locally
generated signal in the case of high rotor speed and/or very low AC terminal voltage (see
Section 29.3).
24.4.5.2 Variable-speed wind turbines: Types C and D
For variable-speed wind turbines, the generato r is a much more controllable element. In
addition to the turbine blade angle, the instantaneous active and reactive power output
of the generator can be controlled.
As mentioned in Section 24.3.1, the variable-speed feature makes it possible to adjust
the turbi ne speed to the optimal speed given in Equation (24.8), thus optimising the
power efficiency coefficient C
P
. This means that the control system must contain some
kind of speed control system and a way to determine a speed reference.
The optimal speed reference is provided by Equation (24.8) or by any other approach
arriving at the same value, such as the speed reference derived from Figure 24.2(b).
Additionally, for dimensioning reasons, the optimal reference speed is normally cut off
at a minimum and a maximum permissible rotational speed correspondi ng to low and
high wind speed situations.
The speed control system can be designed in many different ways. However, they all
share the common feature that the mechanical power input from the rotating system can
be controlled (at least up to an upper limit determined by the incoming wind) and that the
electrical power emitted through the generator also can be controlled (at least in normal
grid situations with nominal voltage). This means it is always possible to control the power
balance in the rotating system and thereby also the speed. Consequently, the actions of the
electrical power control system and the blade angle control system must be coordinated in
some way. This coordination is incorporated in the design process of the control systems.
Control strategies may differ depending on the choices made by the manufacturer. It
would be possible to construct a single control system that could work for all wind
conditions. Another option is to let the blade angle control system control the speed in
high winds, thus leaving it to the power control system to maintain constant, rated
maximum power; in low and medium wind situations, the power control system can
control the speed, thus leaving it to the blade angle control system to optimise the blade
angle to the incoming wind, thereby optimising the power production.
Similar to fixed-speed wind turbines, the blade angle control can also be used for a
preventive rapid power reduction in emergency situations. However, if a short-term
overspeeding in the rotating system is permissible, the power control system will be able
to reduce the generator terminal power more quickly.
Reactive power can also be controlled (see also Chapter 19). This makes it possible to
use wind turbines for voltage control. Currently, this possibility is not made use of very
often. It would seem to be only a matter of time, though, before the grid code will
require large wind farms to supply such ancillary services.
540 The Modelling of Wind Turbines
