Accardi L., Freudenberg W., Obya M. (Eds.) Quantum Bio-informatics IV: From Quantum Information to Bio-informatics
Подождите немного. Документ загружается.


240
The
above observation indicates one way
to
progress
with
classification
of
mulipratitie
states:
different
entanglement
patterns
are
represented
by
equivalence classes
of
pure
states
related
by
local
unitary
actions. However,
already
in
the
case
of
a
tripartite
system,
even
in
its
simplest version con-
sisting
of
3
qubits,
the
classification
turns
out
to
be
much
more
complex
l5
,16
than
the
bipartite
one: local
unitary
equivalence yields
the
following
state
prototypes
with
Ai
~
0,
L:
A;
=
1,
a
:::;
e
:::;
1r.
A general scheme yielding similar
"normal
forms" for
arbitrary
multi-
partite
systems
is known
l9
, minimizing
the
number
of
summands
from a
product
orthonormal
basis,
yet
the
number
of
free
parameters
grows con-
siderably
with
the
number
of
parties.
This
substantial
increase
of
normal
form complexity suggests
the
re-
placement
of
local
unitary
equivalence
with
another,
more
crude
classifica-
tion
scheme.
It
can
be
realized
by
the
so-called
stochastic
LOCC
(SLOCC)
equivalence
20
where, roughly speaking, local
unitary
transformations
are re-
placed
with
local invertible ones.
It
is
the
SLOCC
classification
that
splits
the
set
of 3-qubit
pure
states
into
the
well-known six categories:
separable
states
represented
by
1000),3
types
of
biseparable
ones,
A-BC
represented
up
to
normalization
by
10)
Q9
(100)
+
111))
and
similarly for
AB-C
and
AC-B,
the
W-states
and
, finally,
the
GHZ
type
states
represented
by
(1).
However,
the
passage
to
a
4-qubit
system
reveals
again
the
whole con-
tinuum
of
SLOCC
equivalence classes,
just
like
in
the
LV classification
scheme: one
can
distinguish 9
structural
types
of
pure
state
entanglement
yet
the
complete
SLOCC
classification involves also 4
independent
complex
parameters21.
Natural
convex
structure
of
mixed
state
sets
yields still different
and
much
simpler classification scheme,
based
on
partitions
of
the
set
of
con-
stituents
of
the
system.
An
approach
of
such
type
has
been
developed in
detail
e.g. in
[22].
Suppose
that
the
parties
constituting
a
compound
quantum
system
are
labeled
by
AI"'"
An,
that
is H = HA,
...
A
n
'
Any
partition
of
this
set
of
labels, say
{A~,
.
..
, A;,,} U
...
U {Af, ... ,
A~k}'
corresponds
to
a specific
"coarse-grained" way
of
looking
at
the
entire
system,
i.e.
here
a
k-partite
one. A
pure
state
I'lj!)
E H is called k-separable iff
there

241
Figure
1.
The
structure
of
mixed
states
of
a
3-qubit
system
5
.
exists a
partition
as above
such
that
with
l?,bi)
E Ji Ai
".A~j
, j =
1,
...
, k.
It
is obvious
that
k-separable
states
are
automatically
l-separable
for l < k,
with
respect
to
appropriate
coarser
partitions.
Next
the
notion
of
k-separability
is
extended
to
mixed
states
by
the
usual
convexity
construction:
Definition
2.1.
A
mixed
state
p is k-sepamble,
in
short
p E 'L.k(Ji), iff
it
can
be
represented
as a convex
combination
of
pure
projections
on
k-
separable
vectors,
m
Let
us
stress
that
k-separability
of
individual
l?,bm)
above refers
in
gen-
eral
to
different
partitions
of
the
system
constituents.
The
above
notion
of
k-separability
yields
the
convex
filtration
in
the
set
of
states
'L.(Ji),
'L.(Ji)
.

242
The
simplicity
of
such
partition-based
approach
should
not
overshadow
some of
its
obvious deficiencies, especially
the
fact
that
it
misses
impor-
tant
structural
features
of
states
singled
out
e.g.
in
the
SLOCC
equivalence
scheme. Going
back
to
the
3-qubit
example,
one
can
reveal
5
a finer convex
structure
distinguishing
the
W-type
states
and
GHZ-type
states
among
the
3-partite
entangled
ones, cf. Fig.
1.
The
W-type
states
are
those
which
can
be
expressed
as
convex
sums
of
projectors
on
separable,
biseparable
and
W-type
vectors,
GHZ-type
ones
being
the
complement
in
the
set
of
all
states.
It
should
be
stressed, however,
that
in
practice
one
is
often
inter-
ested
only in gross
entanglement
features, e.g. in
the
distinction
between
genuinely
n-partite
entangled
and
biseparable
states
,
or
between
bisepara-
ble
and
triseparable
ones, etc.,
when
the
partition-based
approach
offers
sufficient means.
In
the
following sections we
shall
describe
in
detail
the
construction
of
an
entanglement
witness
based
on
the
system
Hamiltonian
which
detects
genuinely
entangled
mixed
states
vs.
biseparable
ones.
3.
Construction
of
entanglement
witnesses
An
entanglement
witness
is a versatile
tool
which allows one
to
detect
entangled
states
of a
compound
quantum
system
17.
Let
us recall
its
original
definition
in
the
bipartite
setting
7
•
9
.
Definition
3.1.
A self-adjoint
operator
W E
BCHAB)
is
an
entanglement
witness
iff
Tr(W
0")
~
0 for all
separable
mixed
states
0",
while
Tr(W
[!) < 0
for some
nonseparable
[! (equivalently,
Tr(W
. ) is
nonnegative
on
separable
states,
yet
the
spectrum
of
W
contains
a
negative
eigenvalue). W is
then
said
to
detect
the
entanglement
of
[!.
Entanglement
witnesses
are
directly
related
via
the
Jamiolkowski
isomorphism
18
to
positive
but
not
completely
positive
maps
which
are
basic
for
the
characterization
of
entanglement
ll
.
Although
entanglement
detec-
tion
criteria
based
on
positive
maps
(e.g.
the
famous Peres-Horodecki
partial
transpose
criterion)
are
formally
stronger
than
the
witness-based
ones, yet
globally
they
are
equivalent
in
the
sense
that
for deciding
separability
of
a
given
state
it
takes
in
general all possible
witness-based
tests
and
likewise
all positive
map-based
ones.
The
main
advantage
of
witness-based
detec-
tion
is
its
operational
simplicity,
namely
it
is realized
by
measuring
W in
the
tested
state
[!. Therefore, if W
has
some
direct
physical
meaning,
such
a
procedure
becomes
experimentally
feasible.

243
Figure
2.
The
idea
of a
~C-witness.
It
should
be
noted
that
the
witness technique
can
be
immediat
ely refor-
mulated
to
de
tect
not
the
entanglement
but
any
other
property
of
quantum
states
defining a convex subset
of~.
Let
D.
c
~
be
such a subset. We will
then
call
an
observable W
the
D.c-witness
b
iff Th(W . ) is
nonnegativ
e
on
D.
and
Th(W
Q)
< 0 for some Q ¢
D..
After all,
the
witness technique is
just
a
simple application
of
the
geometric formulation
of
Hahn-Banach
th
eorem:
the
null-space
of
Tr(W
. )
separates
the
convex
set
D.
and
the
external
point
Q,
cf. Fig.
2.
Now, suppose
that
we work
with
a
multipartite
system.
One
can
use
the
set
of
k-separable
stat
es
~k
in
place
of
D.,
to
define a witness dete
cting
the
related
entanglement
category
of
states
(i.e. non-k-separability).
Of
basic interest
are
witnesses
detecting
the
genuine n-fold
entanglem
e
nt,
i.e.
filtering
out
all biseparable
states.
We will focus on
constructing
such
witnesses below.
Examples
of
witnesses of similar
typ
e exist in
literature
5
,
6,23,
and
the
general
method
of
their
construction
proceeds as follows. Let
I~
)
be a fixed
entangled
multipartite
state.
The
witness is defined by
v = a
II:
- :
I~)(~I
,
(2)
where a = maxl
¢)
EiJ.1
(~
I
</I)
1
2
,
i.e.
it
is
the
maximum
squared
overlap
of
I~)
with
states
in
D..
Obviously
I~
)
¢
D.
, for otherwise a = 1
and
V is
not
b
~
replace
s
here
the
set
of
separable
stat
es so, following
th
e
convention,
W
witn
esses
the
property
co
mplementar
y
to
~.
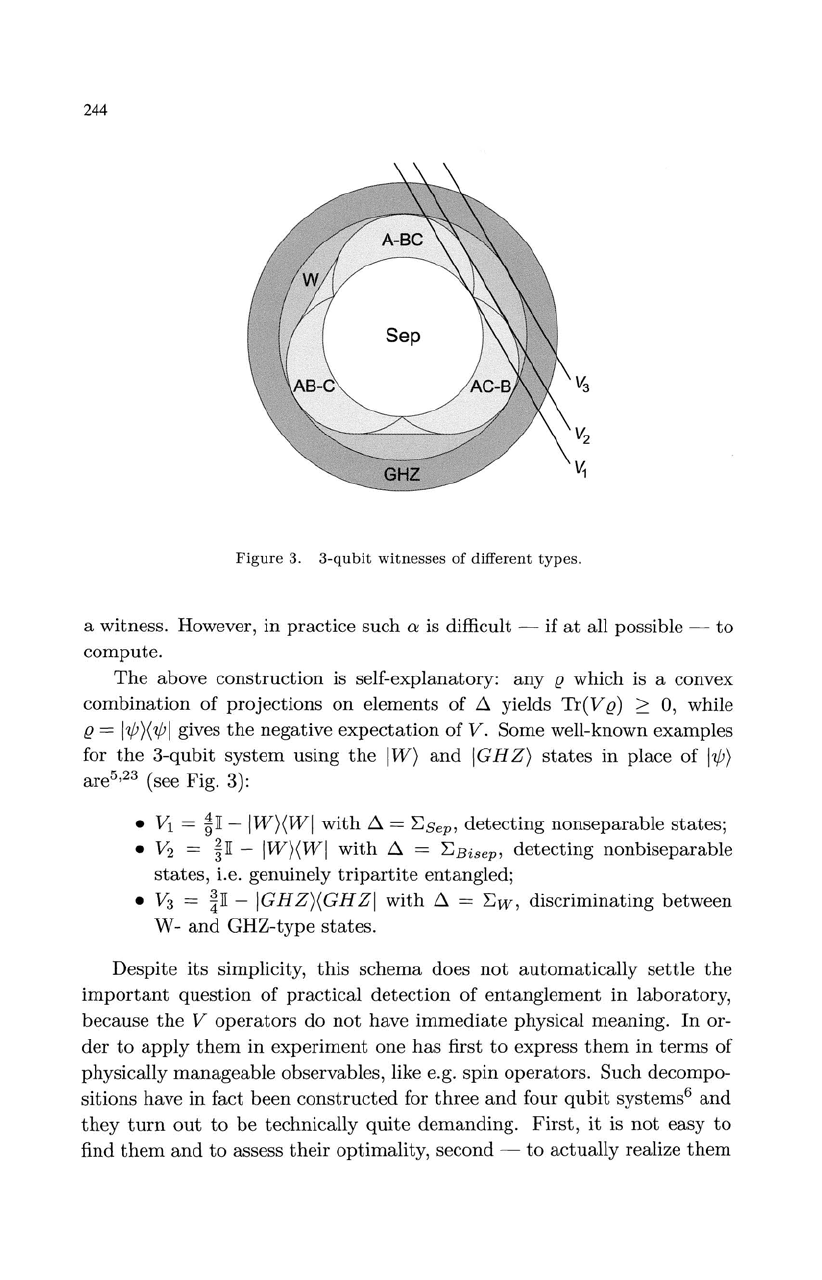
244
Figure
3.
3-qubit
witnesses
of
different
types.
a witness. However,
in
practice
such
a is difficult - if
at
all possible -
to
compute.
The
above
construction
is self-explanatory:
any
12
which is a convex
combination
of
projections
on
elements
of
D.
yields
Tr(V
12)
2:
0, while
12
=
I~,(~I
gives
the
negative
expectation
of
V.
Some well-known
examples
for
the
3-qubit
system
using
the
IW,
and
IGHZ,
states
in
place of
I~,
are
5
,23
(see Fig. 3):
•
VI
=
~][
-
IW,(WI
with
D.
=
~Sep,
detecting
nonseparable
states;
• V
2
=
~][
-
IW,(WI
with
D.
=
~Bisep,
detecting
nonbiseparable
states,
i.e. genuinely
tripartite
entangled;
•
V3
=
~][
- IGHZ,(GHZI
with
D.
=
~w,
discriminating
between
W-
and
GHZ-type
states.
Despite
its
simplicity,
this
schema
does
not
automatically
settle
the
important
question
of
practical
detection
of
entanglement
in
laboratory,
because
the
V
operators
do
not
have
immediate
physical
meaning.
In or-
der
to
apply
them
in
experiment
one
has
first
to
express
them
in
terms
of
physically
manageable
observables, like e.g.
spin
operators.
Such
decompo-
sitions have
in
fact
been
constructed
for
three
and
four
qubit
systems
6
and
they
turn
out
to
be
technically
quite
demanding.
First,
it
is
not
easy
to
find
them
and
to
assess
their
optimality, second -
to
actually
realize
them

245
in
laboratory:
in
the
cases discussed
the
experimental
setup
required
5-15
local
measurement
settings.
We
are
going now
to
explore a slightly different approach, where
the
witness
construction
begins
with
a
true
physical observable
that
is easy
to
measure
24
,25,10.
Let
A
be
such
an
observable.
Then
the
b..
c
-witness is
constructed
as
WA
=
A:-:o:[,
(3)
where
0:
=
inf
l
¢)E.6. (¢IAI¢).
Just
like in
the
case
of
schema
(2), finding
the
exact
value of
0:
may
be
a difficult task. Note, however,
that
once
0:
is known,
it
suffices
to
measure
the
observable A
in
a
state
g,
an
easily
manageable
task,
and
compare
the
resulting
value Tr(Ag)
with
0::
if
the
measurement
outcome
is less
then
0:,
g has
the
desired
property
b..
c
.
To
analyze
the
present
method
closer,
let
us
write
A
in
its
spectral
decomposition form,
with
Ai
and
l1/'i)
being
its
eigenvalues
and
eigenvectors, respectively.
Then
(4)
For a fixed
I¢)
the
sum
in
(4) is simply a weighted
mean
of
eigenvalues.
Let
us
plot
the
range
of
these
mean
values (i.e.
the
image of
b..)
against
the
spectrum
of
A, cf. Fig.
4.
a
Figure
4.
The
image
of
t.
against
the
spectrum
of
A.
We
can
see now
that
in
order
for W A
to
be
a witness one
must
have
Al
<
0:
or,
in
other
words,
at
least
the
ground
state
11/'1)
of A
must
not
belong
to
b...
W A is
then
suitable
to
detect
the
type
of
entanglement
present
in
11/'1)
and
possibly also
in
other
lowest eigenvectors
11/'2)'
...
as long as
they
are
not
of
b..
type.

246
As
it
has
been
said
above,
the
main
difficulty is usually
hidden
in
the
computation
of
a.
It
is
both
the
structure
of
the
set
of
states
~
and
sym-
metry
properties
of
A
that
determine
how
hard
this
task
will eventually
be. Heuristically, one
can
expect
that
determination
of
a will
be
less dif-
ficult
in
the
cases
when
~ is simply
the
set of
separable
states
and
A is
sufficiently
symmetric
with
respect
to
relabeling
of
the
system
components.
A relatively large class of
analytically
tractable
examples is provided
by
spin
lattice
models
with
regular
interaction
patterns,
where
the
respective
hamiltonian
H plays
the
role
of
the
observable A
10.
The
problem
of
finding a
may
be
simplified considerably if
instead
of
its
exact
value
one
uses a reasonable lower
bound
a
::;
a
in
the
witness
construction.
The
resulting
WA will
not
be
optimal
in
the
sense
that
in
general
it
will
detect
less
states
than
the
exact
witness WA: obviously we
will have
Tr(WAO)
~
Tr(WAO) for
any
0,
which is
the
price
to
pay
for
the
simplification
of
determining
a.
We will outline one such
approximation
procedure
below.
Recall
that
a is given
by
(4).
Let
ILl
=
SUPI¢)E~
1(7Pll¢)1
2
.
Since
by
assumption
l7Pl)
tf-
~,
we have 0
::;
ILl
<
1.
An
immediate
lower
bound
to
a is
then
(5)
Indeed,
it
is
the
least possible
mean
of
eigenvalues (4) realized only
if
for
some
¢ E
~
there
is a coincidence
of
null overlaps
(7Pi
I ¢) = 0 for all i
~
3.
An
improvement
of
this
approximation
may
still
be
possible
and
it
depends
on
the
actual
value
of
maximal
squared
overlap
of
17P2)
with
states
in
~.
Let
IL2
=
SUPI¢)E~
1
(7P21
¢)
12.
If
now
IL2
<
1-
ILl'
the
improved lower
bound
to
a is given
by
(6)
One
can
continue
this
procedure
finding
subsequently
IL3'
...
etc.
as
long as
the
obtained
values satisfy
ILk
< 1 -
ILl
-
...
-
ILk-l
at
each step.
In
[1]
we have applied
the
exact
witness
construction
method
based
on
(3)
to
a I-dimensional isotropic Heisenberg
ring
of
n spins
immersed
in a
uniform
magnetic
field
of
controllable
strength
B.
~
was chosen
to
be
the
set of fully
separable
states.
The
resulting
witness was
then
applied
to
thermal
equilibrium
states
of
the
system,
detecting
correctly
their
entan-
glement for a
range
of
field
and
temperature
values.
In
the
next
section,
we
will analyze
the
anisotropic case
and
we will show how one
can
find a

247
lower
bound
of
a
with
the
procedure
just
described
when
~ is
the
set
of
biseparable
states.
4.
Example:
Anisotropic
Heisenberg
spin
chains
In
the
present section we will work
with
the
I-dimensional Heisenberg XXZ
model
with
hamiltonian
given
by
N
H = L
o-ko-k+1
+
0-%0-%+1
+
(1
+
D)a-ko-k+1
+
Bo-
k
,
(7)
k=l
Here D
and
B denote, respectively,
the
nonisotropy
parameter
and
the
strength
of
external
magnetic
field.
The
coupling
constant
J is set
equal
to
1 for simplicity (antiferromagnetic case).
The
Hilbert
space
of
the
model is
1i
=
(C
2
)®N
and
we have used
the
abbreviated
notation
o-k
=
1IQ9··
.Q9o-xQ9
...
Q91I,
where
the
spin
operator
o-X
appears
at
the
k-th
slot,
and
similarly
for
0-%
and
o-k.
Moreover,
the
index
value k = N + 1 is identified
with
1,
dosing
the
chain
in a periodic
manner.
Suppose first
that
we
want
to
use H for
the
construction
of
an
ordinary
entanglement
witness,
that
is,
we
take
~
to
be
the
set
of fully
separable
N-qubit
states
I¢)
=
1¢1)
Q9
...
Q91¢N)·
The
k-th
term
of
(¢IHI¢) evaluates
to
(¢klo-XI¢k)
(¢k+110-
x
l¢k+1)
+
(¢klo-YI¢k)
(¢k+llo-
Y
I¢k+1)
(8)
+
(1
+ D)(¢klo-ZI¢k)
(¢k+110-
z
l¢k+1)
+ B(¢klo-ZI¢k).
Since
I¢k)
vary
independently
on
their
respective Bloch spheres, recall
1
,10
that
we
can
rewrite
the
above using
independent
real variables
Xh,
Yk
and
Zk
in
place
of
the
expectations
of
o-x,
o-y
and
o-z,
(9)
with
additional
constraints
k=
1,
...
,N.
(10)
Minimizing (¢IHI¢) over ~
amounts
to
finding
the
conditional
minimum
of
the
polynomial
in
3N
real variables composed of
terms
(9)
subject
to
the
constraints
(10). As
it
was
argued
in
[1,
10], such a
minimization
can
be
performed
termwise
with
a slight modification of
the
"B"
part
in
(9),
B
Zk
+
Zk+l
h =
Xk
X
k+1
+
YkYk+1
+
(1
+
D)ZkZk+1
+ 2 '
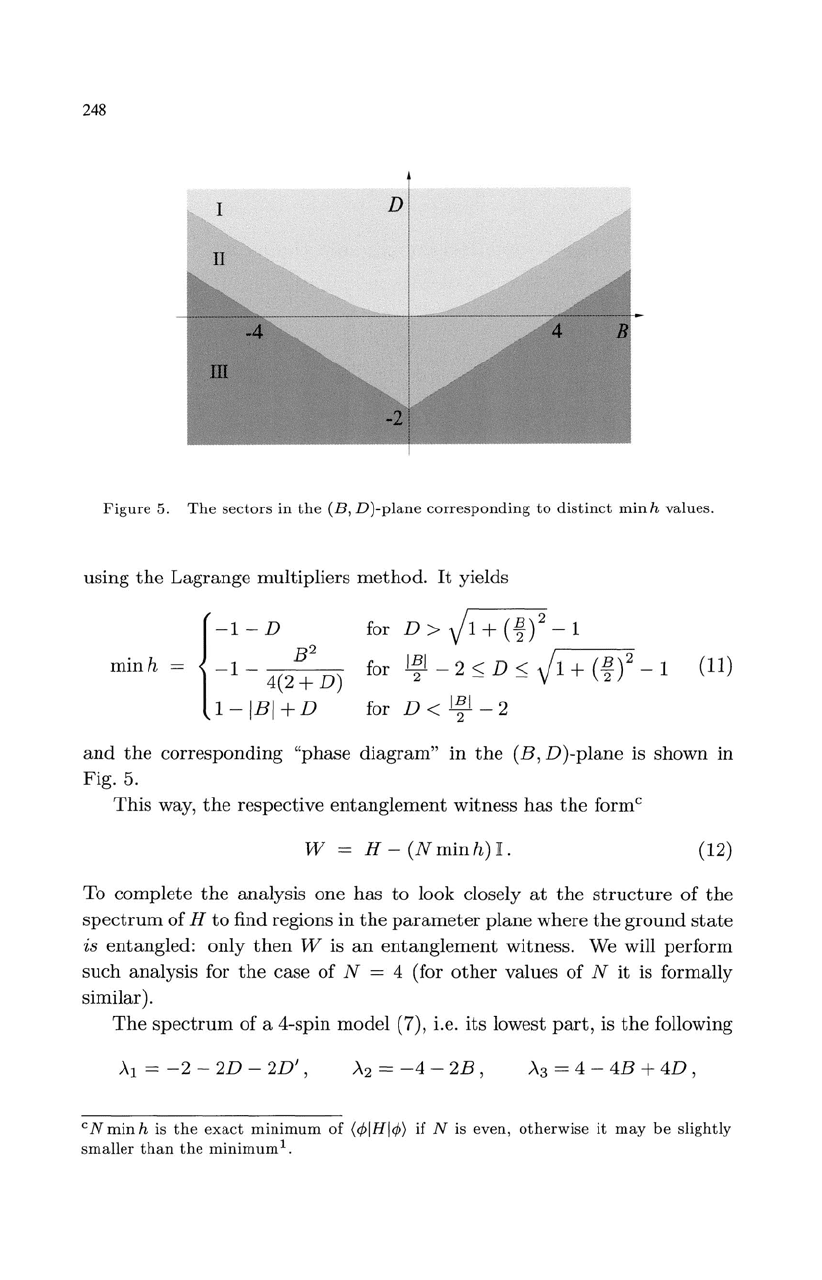
248
Figure
5.
The
sectors
in
the
(B,D)-plane
corresponding
to
distinct
minh
values.
using
the
Lagrange multipliers
method.
It
yields
{
-I-D
.
B2
mm
h =
-1
- 4(2 +
D)
l-IBI
+D
for
for
for D <
@l_
2
2
(11)
and
the
corresponding "phase diagram"
in
the
(B,
D)-plane
is shown
in
Fig.
5.
This
way,
the
respective
entanglement
witness
has
the
forme
W = H -
(Nminh)lI.
(12)
To complete
the
analysis one has
to
look closely
at
the
structure
of the
spectrum
of
H
to
find regions
in
the
parameter
plane where
the
ground
state
is entangled: only
then
W is
an
entanglement
witness. We will
perform
such analysis for
the
case
of
N = 4 (for
other
values
of
N
it
is formally
similar).
The
spectrum
of a 4-spin model (7), i.e.
its
lowest
part,
is
the
following
Al =
-2
-
2D
-
2D'
,
A2
=
-4
-
2B,
A3
= 4 -
4B
+
4D
,
eN
min
h is
th
e
exact
minimum
of
(4)IHI4>)
if
N is even,
otherwise
it
may
be
slightly
smaller
than
the
minimum
1.

249
Figure
6.
The
sectors
in
(B,
D)
plane
where
the
respective
Ai
are
the
lowest
energy
levels,
marked
with
different
shades
of
gray.
The
dashed
line is
the
boundary
between
the
regions I
and
II
of
Fig.
5
and
it
corresponds
to
the
switch
of
minh
value, (11).
where
D'
= V D2 +
2D
+ 9
and
the
corresponding
eigenvectors,
up
to
nor-
malization,
are
1'1/>1)
=
10011)
+
l+D4_DI
10101)
+
10110)
+
11001)
-
1+~+D/1101O)
+
11100)
and
1'1/>2)
=
11110)
-11101) +
11011)
-
10111),
The
states
1'1/>1)
and
1'1/>2)
are
entangled. We have
restricted
here
the
analysis
to
the
B 2 ° halfplane;
the
image for negative B is fully analogous,
the
respective eigenvectors
are
obtained
from
the
current
ones
by
spin
flipping.
The
corresponding level-crossing
diagram,
showing regions
in
the
para-
meter
plane
where different
Ai
become
the
lowest
energy
levels, is
presented
in
Fig.
6.
Thus
1'1/>3)
is
the
ground
state
in
the
region below
the
A2
=
A3
line which is D =
~
-
2;
it
coincides
with
sector
III
of
Fig.
5.
As
1'1/>3)
is
separable, no
entanglement
detection
by
means
of (12) is possible
in
this
domain. Above
the
D =
~
- 2 line
the
ground
state
changes
to
1'1/>2)
and
-
for still larger values
of
D -
to
1'1/>1).
Both
these
domains
have
nonempty
intersections
with
sectors I
and
II
of
Fig. 5 (cf.
the
dashed
parabola
in
Fig. 6
corresponding
to
the
I-II
border).
This
data
allows
one
to
complete
the
detailed
construction
of
the
entan-
glement witness
based
on
H as
prescribed
in
(12). We have
conducted
the
