Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.

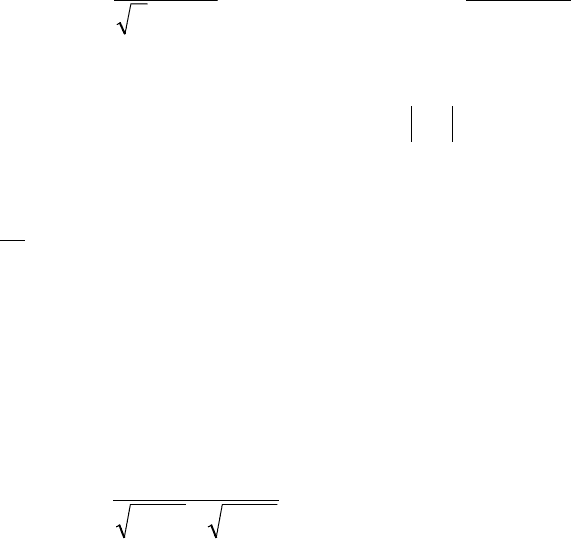
в)
)!2( +
=
nn
x
a
n
; г)
2
2
)sin(
n
xx
a
nn
n
= .
Получить
k
aa ++ ...
1
, где k- наименьшее целое число,
удовлетворяющее двум условиям: k > 10 и
5
1
10
−
+
<
k
a .
761. Дано действительное число )0( >
ε
ε
. Вычислить
∑
∞
=
−
1
13
)3(cos
3
1
n
n
n
, учитывая только те слагаемые, в которых множитель
n
3/1 имеет величину, не меньшую, чем
ε
.
762. Дано действительное число )0( >
ε
ε
. Последо-
вательность ...,,
21
aa образована по следующему закону:
а)
11
22
−−+
=
nn
n
a
n
;
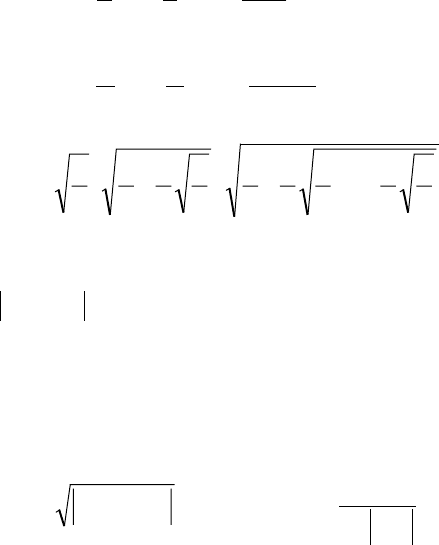
б)
+
−
−
−=
1
1
1...
3
1
1
2
1
1
n
a
n
;
в)
+
−
+
+
−=
)!1(
)1(
1...
!3
1
1
!2
1
1
n
a
n
n
;
г)
2
1
2
1
...
2
1
2
1
2
1
...
2
1
2
1
2
1
2
1
++++⋅=
n
a .
Найти первый член )2(
≥na
n
, для которого выполнено
условие
ε
<−
−1nn
aa .
763. Даны действительные числа х, )0( >
ε
ε
. Последо-
вательность ...,,
21
aa образована по следующему закону: xa =
1
;
далее, для n = 2, 3, ... выполнено:
а)
xaa
nn
24
2
1
−=
−
; б)
1
3
1
3
1
16
−
−
+
+
+
=
n
n
n
a
a
x
a
;

в)
2
1
1
4
2
−
−
+
+=
n
nn
a
x
aa
; г) )(cos
2
1
3
1
2
xaa
n
n
n
−+=
−
.
Найти первый член )2( ≥na
n
, для которого выполнено условие
ε
<−
−1nn
aa . (ограничиться рассмотрением первых
4
10 членов).
764. Рассмотрим последовательность ,...,,
10
dd периметров,
вписанных в данную окружность многоугольников с удваивающимся
числом сторон. Радиус окружности - данное действительное число r.
Первый из рассматриваемых многоугольников - шестиугольник.
Вычислить )0( >nd
n
, для которого
6
1
10
−
−
<−
nn
dd .
765. Даны действительные числа х, )0,10( ><<
ε
ε
x .
Вычислить с точностью
ε
значение
∑
∞
=1
)(
2
k
k
x
.
766. Даны действительные числа )0,0(,, >>>
ε
ε
baba .
Последовательности ...,,...,,,
2121
yyxx образованы по закону

111111
),(
2
1
,,
−−−−
=+===
kkkkkk
yxyyxxbyax . Найти первое
n
x
такое, что
ε
<−
nn
yx .
767. Даны действительные числа a, b. Последовательности
...,,...,,,
2121
yyxx образованы по следующему закону:
).5.0sin(5.0),5.0cos( nbanynbax
nn
−=+= Получить
kk
yx /, где k-
наибольшее натуральное число удовлетворяющее двум условиям:
20≤k и
3
10
−
>
k
y .

§ 25. Физика
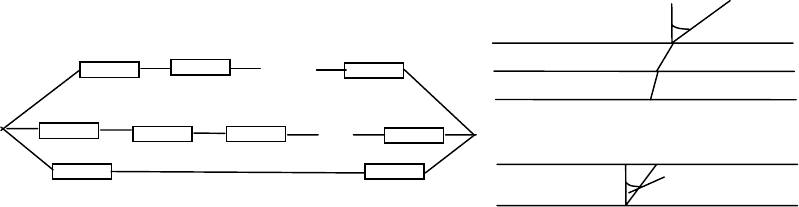
768. Группа параллельно соединенных сопротивлений,
изображенная на рис. 46, a, задается неотрицательными числами
i
rrr ...,,,
21
- значениями сопротивлений. Последовательное
соединение ряда таких групп, показанное на рис. 46, б, задается так:
сначала идут значения сопротивлений входящих в первую группу,
затем - некоторое отрицательное число, затем - значения
сопротивлений, входящих во вторую группу, затем - некоторое
отрицательное число и т.д. После значения последнего сопротивления
последней группы идут два отрицательных числа. Рассчитать
сопротивление соединения.
. . .
. . .
. . .
. . .
. . .
a б
Рис. 46
769. Аналогично предыдущей задаче, рассчитать сопротивление
параллельного соединения последовательных груп п (рис. 47), вновь
предполагая, что каждая группа задается рядом значений
сопротивлений, за которым идет отрицательное число, а вслед за
значением последнего сопротивления последней группы идут два
отрицательных числа.
770. Прозрачная пластина состоит из т слоев, показатели
2
1
n
n
α
m
n
β
. . .
. . .
Рис. 47 Рис. 48
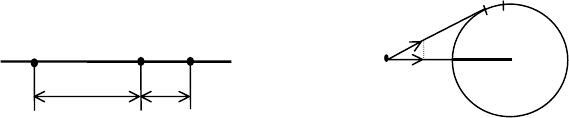
преломления которых
m
nn ,...,
1
. Луч входит в пластину из вакуума под
данным углом
α
(рис. 48). Найти угол
β
, под которым луч пересекает
последний слой.
771. На воду опущен шар радиуса r, изготовленный из вещества
плотности )1( <
ρ
ρ
. Найти расстояние центра шара от поверхности
воды.
772. На прямой находятся три положительных заряда величины
321
,, qqq , так, как показано на рис. 49.
Определить расстояния от заряда
1
q до точек, в которых
равнодействующая сил отталкивания зарядами
321
,, qqq некоторого
четвертого положительного заряда равна нулю.
1
q
2
q
3
q
Рис.49 Рис.50
q
1
l
2
l

773. Найти силу, с которой точечный заряд
6
10
−
=q Кл
притягивается к тонкому непроводящему кольцу радиуса R = 0.1 м.
Заряд расположен в плоскости кольца. Кольцо равномерно по всей
длине заряжено с плотностью заряда
м
Кл
102
7−
⋅=v . Расстояние от
заряда до кольца равно l = 0.1м. Электрическая постоянная равна
ε
0
12
2
885 10=⋅
⋅
−
.
Кл
Н
м
. Для вычислений разбить кольцо на 100 равных
частей и считать каждую часть точечным зарядом величины
100
2 R
v
π
.
Рассмотреть проекции кулоновых сил на прямую, соединяющую
заряд q с центром кольца (рис. 50).
774. «Кривая погони». В точке Р находится собака, а в точке
Q - заяц. Расстояние от Р до Q равно 100 м (рис. 51, а). Заяц бежит
вдоль прямой l, образующей угол 45° с отрезком PQ, с постоянной
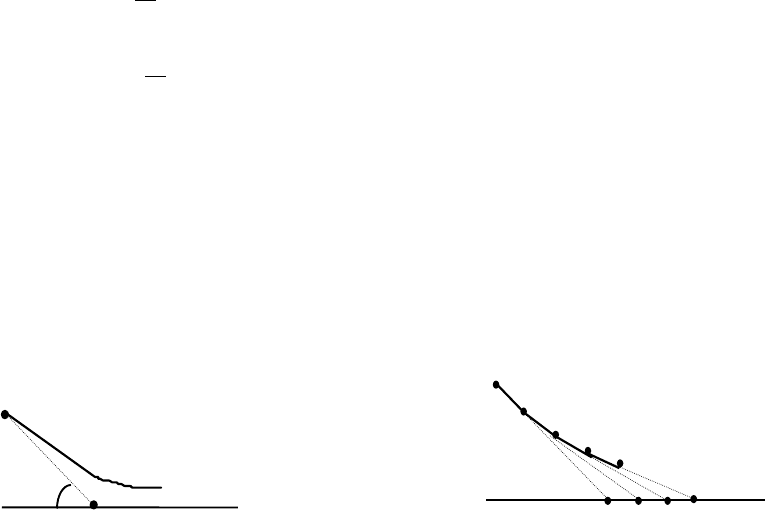
скоростью
с
м
5
. Собака бежит все время в направлении зайца со
скоростью
с
м
10
. Найти траекторию движения собаки в течение 10
с. Для приближенного решения предлагается заменить кривую
ломаной линией. Считается, что в первую секунду заяц вбегает
отрезок QQ
′
, собака -
P
P
′
, во вторую секунду заяц пробегает
отрезок QQ
′′′
и т. д; собака принимает решение о направлении
погони ровно один раз в секу нду ( рис. 51, б ).
P P
45°
Q l Q Q
′
Q
′′
Q
′′′
l
а б
Рис. 51

775. Вернуться к предыдущей задаче. Вычислить
приближенно (заменой кривой на ломаную) длину траектории
собаки, рассматривая первые 15 с погони.
776. Пусть на плоскости задан угол АОВ и из некоторой
точки Р внутри угла выпущен биллиардный шар, который
отражается от сторон угла как от бортов по закону «угол падения
равен углу отражения». Доказать, что после нескольких отражений
шар начнет удаляться от вершины угла (рис. 52, а). Это
обстоятельство объясняет трудности игры на биллиарде: угол
биллиарда не затягивает, а отторгает шар.
Рис. 52
y
A y = kx
P
α
(a,b)
O B
x
б
а
