Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию

Подождите немного. Документ загружается.

546. Даны натуральные числа n, m, символы s

, ...., s

(m < n).

Получить последовательность символов:

а) s

m + 1

, s

m + 2

, ..., s

, s

, ..., s

;

б) s

m + 1

, s

m + 2

, ..., s

, s

, ..., s

;

в) s

, s

n – 1

, ..., s

m + 1

, s

, ..., s

547. Даны натуральное число n, символы s

, ...., s

. Известно, что

в последовательность s

, ...., s

входит по крайней мере один пробел.

Пусть m таково, что s

– это первый по порядку пробел, входящий в

, ...., s

(m заранее неизвестно). Выполнить преобразования а), б), в),

сформулированные в предыдущей задаче.

548. Даны натуральное число n, символы s

, ...., s

. Получить те

символы, принадлежащие последовательности s

, ...., s

, которые

входят в эту последовательность по одному разу.

549. Даны натуральное число n, символы s

, ...., s

. Получить

последовательность символов, содержащую только последние

вхождения каждого символа с сохранением взаимного порядка этих

вхождений.

550. Даны натуральные числа k, m, l, символы

, ...., s

, t

, ...., t

, u

, ...., u

. Получить по одному разу те символы,

которые входят одновременно во все три последовательности.

551. Даны натуральное число n, символы s

, ...., s

. Будем

рассматривать слова, образованные входящими в последовательность

, ...., s

символами (см. задачу 269). Ниже описываются

преобразования, каждое из которых следует произвести при

выполнении указанного условия. Затем последовательность вне

зависимости от того, подвергалась она или нет преобразованию,

должна быть отредактирована следующим образом. Должны быть

удалены группы пробелов, которыми начинается и заканчивается

последовательность, а каждая внутренняя группа пробелов должна

быть заменена одним пробелом.

Преобразования:

а) если общее количество слов больше единицы и нечетно, то

удалить первое слово;

б) если последнее слово начинается буквой а и общее число

слов больше единицы, то переставить последнее слово в начало

последовательности, отделив его пробелом от s

;

в) если первое и последние слова совпадают и общее число слов

больше единицы, то удалить первое и последнее слова, а оставшиеся

символы переставить в обратном порядке.

552. Даны символы s

, s

, .... Известно, что символ s

отличен от

точки и что среди s

, s

, .... имеется хотя бы одна точка. Пусть s

, ...., s

– символы, предшествующие первой точке (n заранее неизвестно).

Получить:

а) последовательность s

, s

n-1

, ..., s

;

б) последовательность s

, s

, ..., s

, если n – нечетное, и

последовательность s

, s

, ..., s

, если n – четное.

553. Если требуется хранение последовательности, число

членов которой ограничено сверху некоторым известным числом N, то

можно использовать для хранения последовательности массив с N

элементами, занимая, таким образом, память вычислительной машины

с некоторым запасом. Это позволяет обойтись без списков.

а) Вернуться к задаче 531, считая, что n ≤ 1000.

б) Вернуться к задаче 532, считая, что n ≤ 1500.

в) Вернуться к задаче 550, считая, что k ≤ 1000, m ≤ 1000,

l ≤ 100.

г) Вернуться к задаче 550, считая, что k + m + l ≤ 2000.

Следует иметь в виду, что если используется несколько таких

массивов, то су ммарный излишек занятой памяти может оказаться

слишком большим для того, чтобы можно было воспользоваться этим

приемом.

ГЛАВА ΙΙ

ЗАДАЧИ ПО ТЕМАМ

§ 15. Целые числа.

554. Дано натуральное число n. Получить все пифагоровы

тройки натуральных чисел, каждое из которых не превосходит n, т. е.

все такие тройки натуральных чисел a, b, c, что

+ b

= c

(a ≤ b ≤ c ≤ n).

555. Треугольником Паскаля называется числовой треугольник

1 1

1 2 1

1 3 3 1

1 4 6 4 1

. . . . . . . . . . . . . . . . .

в котором по краям стоят единицы, а каждое число внутри равно

сумме двух стоящих над ним в ближайшей строке сверху.

Дано натуральное n. Получить первые n строк треугольника

Паскаля.

556. Для чисел Фибоначчи u

, u

, .... (см. задачу 144)

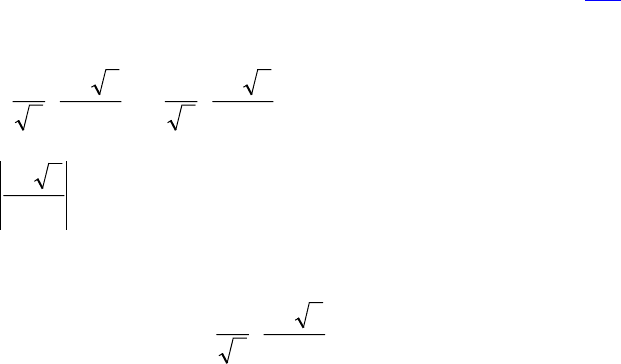
справедлива формула Бине

−

, k = 0, 1, ....

Так как

−

, то для больших k выполнено приближенное

равенство

≈

Вычислить и округлить до целого все числа

(k = 0, 1, ..., 15). Вычислить

1510

...,,, uuu по формулам

2110

;1;0

−−

+===

kkk

uuuuu (k = 2, 3, …) и сравнить результаты.

557. Дано натуральное число n (n ≥ 2). Найти все меньшие n

простые числа, используя решето Эратосфена. Решетом Эратосфена

называют следующий способ. Выпишем подряд все целые числа от 2

до n. Первое простое число 2. Подчеркнем его, а все большие числа,

кратные 2, зачеркнем. Первое из оставшихся чисел 3. Подчеркнём, его

как простое, а все большие числа, кратные 3, зачеркнем. Первое число

из оставшихся теперь 5, так как 4 уже зачеркнуто. Подчеркнем его как

простое, а все большие числа, кратные 5, зачеркнем и т. д.:

3,4,5,6,7,8,9,10,

558. Дано натуральное число n. С помощью решета Эратосфена

(см. предыдущую задачу) найти четверки меньших n простых чисел,

принадлежащих одному десятку (например, 11, 13, 17, 19).

559. Дано натуральное число n. Найти все меньшие n числа

Мерсена. (Простое число называется числом Мерсена, если оно может

быть представлено в виде 2

– 1, где р – тоже простое число.)

560. Два натуральных числа называют дружественными, если

каждое из них равно сумме всех делителей другого, кроме самого

этого числа. Найти все пары дружественных чисел, лежащих в

диапазоне от 200 до 300.

561. Дано натуральное число n. Среди чисел 1, ..., n найти все

такие, запись которых совпадает с последними цифрами записи их

квадрата (как, например, 6

= 36, 25

= 625 и т. д.).

562. Натуральное число из n цифр является числом Армстронга,

если сумма его цифр, возведенных в n-ю степень, равна самому числу

(как, например, 153 = 1

+ 5

+ 3

). Получить все числа Армстронга,

состоящие из двух, трех и четырех цифр.

563. Назовем натуральное число палиндромом, если его запись

читается одинаково с начала и с конца (как, например, 4884, 393, 1).

а) Найти все меньшие 100 натуральные числа, которые при

возведении в квадрат дают палиндром.

б) Найти все меньшие 100 числа – палиндромы, которые при

возведении в квадрат также дают палиндромы.

564. Рассмотрим некоторое натуральное число n. Если это не

палиндром, то изменим порядок его цифр на обратный и сложим

исходное число с получившимся. Если сумма не палиндром, то над ней

повторяется то же действие и т. д., пока не получится палиндром. До

настоящего времени неизвестно, завершается ли этот процесс для

любого натурального n.