9-й Международный симпозиум по электромагнитной совместимости и электромагнитной экологии

Подождите немного. Документ загружается.

521

MAGNETIC FIELD DISTORTION WHILE UNDERGROUND

DETONATION OF SMALL POWER CHEMICAL BLASTING CHARGE

ILATOV

USSIA

UTIN

USSIA

SENOFONTOVA

USSIA

OLOCHKOV

USSIA

ERASIMCHUK

USSIA

FSUE “VNIIA”, e-mail: vniia@vniia.ru

When performing work under the ISTC Project No.

835 Investigation of Electromagnetic Signals

Accompanying Underground Chemical Blasts there were

carried out model underground blasts of chemical

explosive charges in order to study characteristics of

electromagnetic distortion generated by detonation of

explosives. This paper represents routine of experiments,

typical experimental results and qualitative model for

interpreting magnetic field disturbance.

Induction type sensors were used for measuring of

the magnetic field disturbance. Signals from the sensors

were recorded using SONY two-channel analog audio

recorders MZ-R50. Explosive charge detonation was

initiated using igniting fuse. After the experiments the

recorded analog data was converted into digital form

using TDS-540D oscilloscope.

Fig. 1 shows typical transient processes obtained for

one of the underground explosions; Table 1 includes the

parameters of the blast; orientation of the sensors relative

to the blast epicenter is given in Fig. 2.

Fig. 1. Magnetic field/

Fig. 2. Orientation of the sensors relative to the blast

epicenter.

Table 1. Parameters of the blast

Date, No. and type of

blast

02.07.99, No. 21, camouflet at

2.3 m depth

Charge Cylinder of TH 50/50,

D 60 х 420 mm

weight 2.0 kg

Charge orientation Horizontal (East - West)

Detonation direction East - West

The well-known seismoelectrical and magnetic

induction effects are taken as a basis of the qualitative

model interpreting experimental results obtained. While

developing the model the following assumptions and

hypotheses were taken: explosive charge detonation

causes radial movement of ambient soil under the action

of propagating shock wave increasing its conductivity

due to the appearance of seismoelectrical effect; in the

process of conducting region expansion the current

caused by magnetic induction effect is induced inside it.

This current causes short-term disturbance of the

magnetic field. The direction and value of the induced

current are determined by the conducting region

expansion velocity, its conductivity, as well as direction

and module of the Earth magnetic field vector.

Acknowledgments - The work fulfilment was

financially supported by the ISTC under Project No. 835.

North

West

№1

№2

№3

Blast

epicenter

East

South

522

НОВЫЕ ПРИНЦИПЫ ОБЕСПЕЧЕНИЯ МОЛНИЕЗАЩИТЫ В

СИСТЕМЕ ПРЕДОТВРАЩЕНИЯ УДАРОВ МОЛНИЙ DAS ОТ

КОМПАНИИ LEC

С.

Н.

ЮРЕНКОВ

ОССИЯ

К.

В.

РМАКОВ

ОССИЯ

ООО «АСК Контур», emc@askkontur.ru,

ООО «Газпромэнергодиагностика», e-mail: of-

fice@gazpromenergy.ru

Аннотация. В докладе рассматриваются принцип работы, преимущества и опыт применения системы

молниезащиты Dissipation Array System® (DAS®) от компании LEC (США).

Abstract. A principle of the work, advantages and experience of the using the lightning protection from di-

rect strikes – Dissipation Array System® (DAS®) from company LEC (USA) are considered in the paper.

Введение

Несмотря на наличие систем молниезащиты

(МЗ), аварии, вызванные молниевыми разрядами

(МР) в нефтяной отрасли, поражают ежегодно до 8%

объектов и их коммуникаций [1]. По данным МЧС

России только затраты на ликвидацию последствий

аварий на нефтяных объектах составляют от 1,5 до

10 млн. долларов США. Имеется много фактов, ко-

гда после первого удара молнии, молниеприемное

устройство не воспринимает последующие разряды.

В качестве примера можно привести анализ причин

аварии на резервуаре РВС 20000 №22 Александровской

нефтеперекачивающей станции [2]. По показаниям оче-

видцев у резервуара РВС 20000 №22 возникли подряд

два разряда молнии: первый был принят отдельно стоя-

щим в 5 м от резервуара молниеприемником, а второй

пришелся непосредственно в кровлю резервуара. После

попадания МР в кровлю воспламенились пары нефти в

свободном пространстве резервуара.

Расследованием причин аварии установлено,

что МЗ была выполнена в полном соответствии с

требованиями действующей нормативной докумен-

тацией (НД) при помощи отдельно стоящих молние-

отводов на расстоянии 5м и высотой 45 м. Резервуар,

его система молниезащиты, заземление эксплуатиро-

вались так же в соответствии с НД. Причиной удара

второго разряда молнии не в молниеприемник, а в

кровлю резервуара, комиссия управления Западно-

Сибирского округа Госгортехнадзора России назвала

«снос ветром ионизированного канала воздуха».

Это говорит о том, что существующие системы

МЗ не обеспечивают на практике достаточный уро-

вень защиты от прямых МР. Таким образом, возни-

кает реальная неизбежность поражения защищаемых

объектов и персонала.

Предотвращение прямых ударов молний

Как видно из приведенного выше примера, пря-

мые удары молнии происходят даже в защищенные

объекты, а их последствия трудно переоценить. По-

мимо прямых ударов молний возможны удары в

близлежащие заземленные конструкции и объекты.

Такие явления вызывают так называемые «вторич-

ные воздействия» молний на объекты инфраструкту-

ры нефтегазовых предприятий. Можно выделить

четыре основных [4]:

1. Блуждающие токи

2. Электромагнитные импульсы

3. Электростатические импульсы

4. Связанный заряд

Все они могут приводить к возгораниям и взры-

вам либо к выходу из строя контрольно измеритель-

ной аппаратуры и автоматики. Как следствие можно

сделать вывод, что предотвращая прямые удары в

критически важные объекты и их окружение можно

снизить необходимость защиты каждой точки потен-

циально подверженной индуцированным токам и

минимизировать прочие требования к защите от пе-

ренапряжений.

В 1971 году компания Lightning Eliminators &

Consultants, Inc. (США) разработала систему

Dissipation Array ® System (DAS®), позволяющую

полностью исключить попадание молнии в защи-

щаемую область.

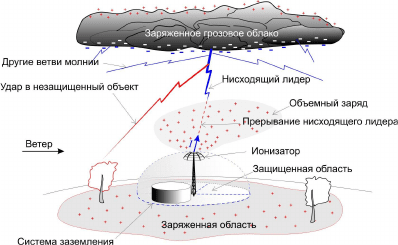
Работа системы основана на принципе точечной

разрядки, заключающейся в стекании заряда с острия

многочисленных иголок в окружающую атмосферу и

создания тем самым объемного заряда, препятствую-

щего развитию восходящих лидеров и задерживающих

движение нисходящих лидеров молнии (Рис. 1). В ре-

зультате молниевый разряд не попадает в защищаемый

объект, а разряжается в незащищенной области.

Рис. 1. Предотвращение попадания молнии с

помощью Dissipation Array ® System компании LEC.

523

DAS ® состоит из трех основных элементов:

1. Ионизатор. Это основной элемент системы

молниезащиты, содержащий тысячи иголок, перено-

сящих заряд, собранный системой заземления в ок-

ружающую атмосферу, создавая тем самым облако

объемного заряда.

При увеличении электромагнитного поля, вы-

званного надвигающимся грозовым фронтом, тради-

ционные стержневые молниеприемники формируют

восходящие стримеры, которые провоцируют удар

молнии. Многоточечный ионизатор напротив, запус-

кает процесс ионизации при несколько большей на-

пряженности поля, но при его увеличении, иониза-

ционные токи экспоненциально возрастают. По-

скольку ионы распределяются по большой площади,

никаких стримеров не возникает.

2. Система заземления. Для работы системы не-

обходимо качественное заземление. Система сбора

зарядов является источником заряда, переносимого

ионизатором в атмосферу. Как только образуется

положительный заряд, наведенный грозовым фрон-

том на поверхность земли, его часть собирается сис-

темой сбора зарядов.

Система сбора зарядов подобна обычной систе-

ме заземления, но она является приемником, а не

системой заземления для растекания токов молний.

По сути, их назначения абсолютно противоположны.

3. Система переноса заряда. Система сбора за-

рядов соединена с ионизатором с помощью низко-

омного проводника, который обеспечивает прямой

перенос заряда к ионизатору. По сравнению с тради-

ционными молниеприемниками этот проводник не-

сет существенно меньший ток и предназначен не для

переноса огромных токов молнии, а для соединения

частей системы в единое целое. Максимальный ток

не превышает нескольких миллиампер и не вызывает

никаких вторичных воздействий, имеющих место

при работе традиционных систем молниезащиты.

Предупреждение формирования восходящего

лидера от любого защищаемого объекта

Предупреждение формирования восходящих

лидеров от любого защищаемого объекта, способных

создать проводящий канал и инициировать удар

молнии в объект. Такие лидеры обычно иницииру-

ются объектами, высота которых более 200 метров,

или объектами в горной местности на такой высоте,

где суммарный подъем допускает напряжение на

наивысшей точке в пределах 10

вольт во время про-

цесса разряда.

Исследования, проведенные российским учены-

ми Э.М. Базеляном и его коллегами, сформулирова-

ли условия для уменьшения риска поражения объек-

та молнией. Было доказано, что использование оп-

тимизированного ионизатора способно создать и

поддерживать объемный заряд в зоне потенциально-

го риска удара молнии. Также было обнаружено, что

объемный заряд способен предотвращать зарожде-

ние групповых лидеров.

Редкие прорывы были замечены в областях, где

разряды часты и преобладают именно восходящие

молнии. В этих случаях плотность объемного заряда

должна быть существенно выше, чем нисходящий

отрицательный разряд. Пиковые молниевые токи и

сопровождающие их заряды для положительных

разрядов начинаются от земли и достигают пиковых

значений тока в 200 000 ампер. Отрицательные раз-

ряды, нисходящие от грозовой зоны, достигают пи-

ковых значений около 80 000 ампер. Поэтому в об-

ластях, где преобладают позитивные разряды, объ-

емный заряд должен быть увеличен примерно в два

раза. Электростатические поля в этих случаях значи-

тельно выше, что позволяет увеличить ионизацию.

Предупреждение касания объекта нисходя-

щими лидерами

Предупреждение касания объекта нисходящими

лидерами – значительно более сложная задача. По-

следние 100 метров до объекта молниевый лидер

движется со скоростью около 400 метров в секунду.

При таких скоростях необходимое количество объ-

емного заряда должно быть готово прежде, чем бу-

дет сформирован встречный лидер, за 50-100 милли-

секунд до прибытия нисходящего лидера.

Исследования компании LEC и полевые испы-

тания доказали, что корректно спроектированный

ионизатор DAS способен реагировать и предупреж-

дать касание молнии, генерируя комбинацию пред-

разрядного объемного заряда и реактивного объем-

ного заряда высокой плотности при приближении

молниевого лидера.

Предразрядный объемный заряд определяется

размером ионизатора, электростатическим полем,

временем между разрядами и скоростью перемеще-

ния объемного заряда. Комбинация электростатиче-

ского поля восходящих потоков, создаваемых грозой

и силами согласно закону Кулона, вызывают непре-

рывный поток ионов и постоянное перемещение за-

ряда между ионизатором и грозовой областью, как

описывал физик атмосферы Д-р Альтон Чалмерс [5].

Объемный заряд препятствует образованию группо-

вых лидеров при высокой плотности заряда.

Чтобы понять сущность процесса фазы преры-

вания молниевого лидера, приближающегося к DAS,

необходимо понять состояние лидера перед касани-

ем объекта. Это продемонстрировано на рис. 1 –

схема, которая поможет понять работу DAS. Она

иллюстрирует процесс за миллисекунды до преры-

вания. Обратите внимание, что молния имеет не-

сколько ответвлений. Все примерно на одном рас-

стоянии от земли, одна должна коснуться поверхно-

сти. Целью является не дать ей коснуться DAS или

объекта в защищенной области. Рис. 1 иллюстрирует

эту ситуацию на примере мачты, защищенной DAS.

DAS реагирует на приближение лидера увеличением

плотности объемного заряда.

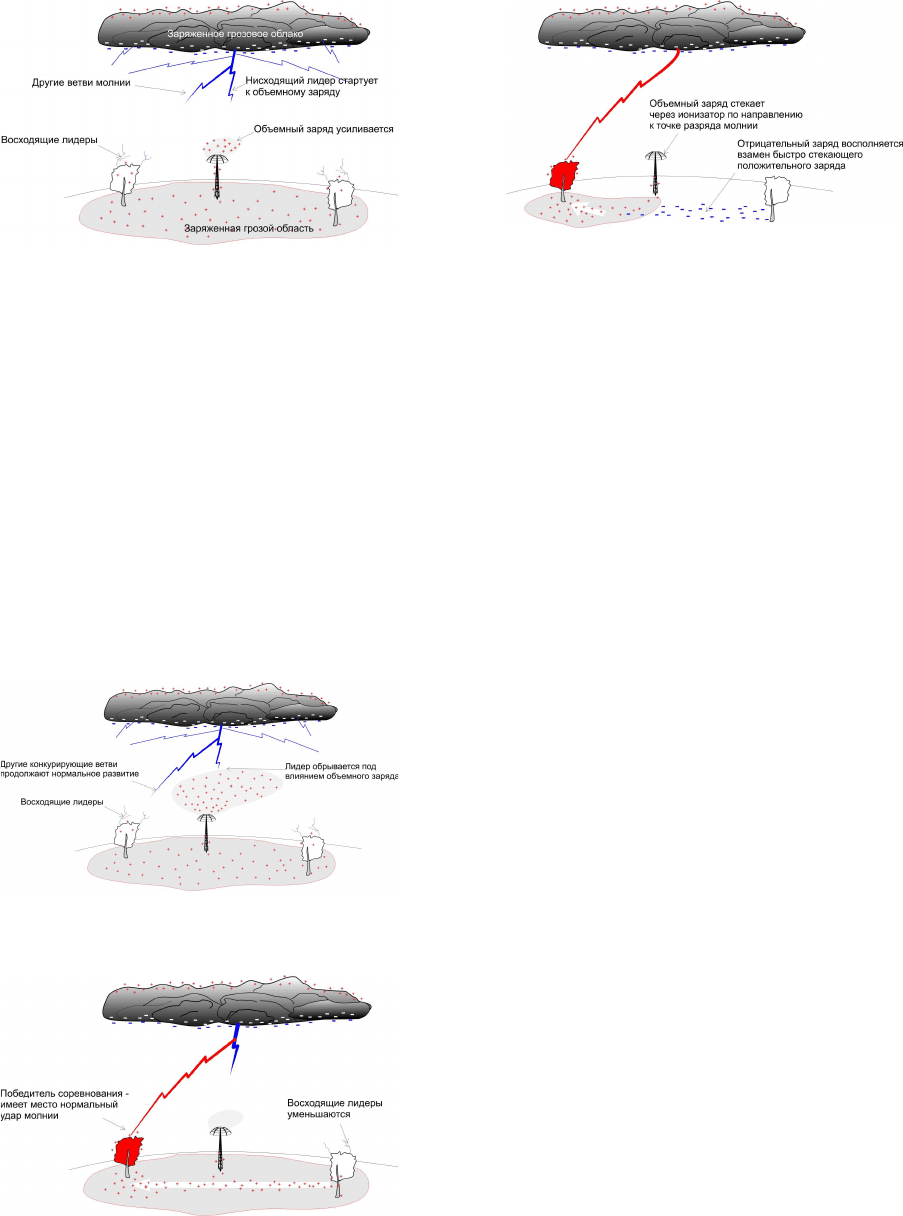
524

Рис. 2. Ветвь молнии приближается к DAS.

Рис. 2 показывает реактивный пространственный

заряд, созданный приближающейся ветвью молниевого

лидера. Результирующий плотный объемный заряд

подавляет формирование встречного лидера и ситуация

развивается, как показано на Рис. 4, а затем – на Рис.5.

На Рис. 4 одна ветвь теперь касается дерева, все ос-

тальные стримеры замкнуты. И наконец, объемный

заряд, сформированный DAS, также замыкается через

ионизатор, создавая обратный разрядный ток, продол-

жающийся только несколько миллисекунд. Все заряды,

содержащиеся в ветвях и вокруг ионизатора, принима-

ют участие в процедуре нейтрализации, как показано

на Рис.5. Земля возвращается к нормальному отрица-

тельному состоянию, когда грозовые области разряжа-

ются или уходят.

Рис.3. Реактивный объемный заряд, созданный

приближающимся лидером.

Рис. 4 Молниевая ветвь касается дерева. Ос-

тальные ветви уходят.

Рис.5. Заряд уходит в молниевый канал. Уста-

новка возвращается в нейтральное состояние.

Процесс втягивания занимает от одной до трех

миллисекунд. Это соответствует примерно 100 мКл

(0,1 А с). Тем не менее, результирующая скорость

может достигать от 30 до 100 кА/мс. В то же время

этот обратный ток не несет никакой разрушительной

энергии, т.к. передается очень маленький заряд за

очень короткий промежуток времени.

Защищенная область

Из принципов работы DAS вытекают три фак-

тора, влияющие на размер и форму защищенной об-

ласти:

1. Количество ветвей молниевого разряда;

2. Расстояние между ветвями;

3. Удаленность DAS от нисходящего лидера.

Количество ветвей лидера определяет вероят-

ность того, что одна из них приблизится к установке

DAS. Обычный лидер стартует и производит не-

сколько ветвей; тем не менее, к моменту, когда он

достигнет расстояния нескольких сот метров от зем-

ли, количество ветвей многократно увеличивается,

как показано на Рис. 2. Поэтому вероятность удара

молнии в одну из незащищенных DAS точек равна

один к количеству ветвей молнии.

Таким образом, DAS задерживает развитие при-

ближающегося лидера-ветви с целью переноса удара

в другое место.

Заключение

О состоятельности тех или иных научных ут-

верждений можно судить на основании опыта их

применения. Статистика работы DAS формировалась

на протяжении 34 лет на более чем 2400 объектах, и

ее наработка составляет более 30 000 системных лет

работы. Репрезентативность этой выборки не может

вызывать сомнений.

Одним из подтверждений могут служить ре-

зультаты шестилетних наблюдений с мая 1995 по

май 2001, производимых на атомной электростанции

Browns Ferry Nuclear Plant (Алабама, США). Иониза-

тор был установлен на трубу станции высотой более

180 м. На рис. 6 и 7 показаны результаты наблюде-

ний ударов молний в радиусе 500 м и 5 км за три

года до установки ионизатора и три года спустя. Чи-

словые значения показаны в таблице 1. Как видно из

таблицы наблюдается снижение количества ударов

молний на 80% в радиусе 500 м от места установки

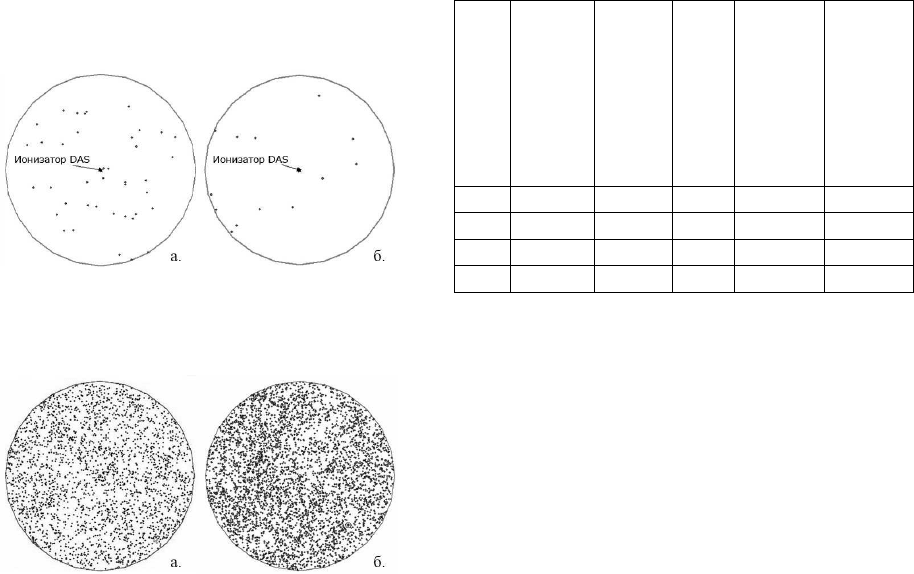
525

ионизатора на фоне общего увеличения молниевой

активности в радиусе 5 и 10 км.

Рис. 6. Молниевая активность в радиусе 500 м

от трубы в течении 3-х лет до (а) и трех лет после (б)

установки DAS.

Рис. 7. Молниевая активность в радиусе 5 км от

трубы в течении 3-х лет до (а) и трех лет после (б)

установки DAS.

Рас

сто-

яни

е,

км

Кол-во

ударов

до ус-

танов-

ки DAS

Кол-во

ударов

после

уста-

новки

DAS

Из-

мене

ние

Ожи-

даемое

количе-

ство

ударов

Изме-

нение,

приве-

денное

к ожи-

даемо-

му,

0,5 40 13

-68

-80

5 2630 4327 +65 4327 0

10 11277 18688 +66 18688 0

16 33685 55199 +64 55199 0

Таблица 1. Количество ударов молний в течение

трех лет до и трех лет после установки DAS.

Литература

1. Черкасов В.Н. Защита взрывоопасных со-

оружений от молний и статического электричества. –

М.: Стройиздат, 1984 – 81 с.

2. Надточин В.И. Анализ причин аварии на ре-

зервуаре РВС 20000 №22 Александровской НПС ма-

гистрального нефтепровода «Александровское –

Анжеро – Судженск» // Безопасность труда в про-

мышленности.

3. Preventing direct strikes Roy B. Carpenter, Jr.

Lightning Eliminators & Consultants, Inc. August 2005.

4. Lightning Strike Protection By Roy B. Carpen-

ter, Jr. Mark M. Drabkin, PhD. Lightning Eliminators &

Consultants, Inc. 2005

5. Moore, Charles B., “Results of the Lightning

Strike Contest,” Langmuir Lab, June 2001,

(unpublished).

526

DETAILS INCLUDED IN THE CALCULATION

OF GEOMAGNETICALLY INDUCED CURRENTS

N ELECTRIC POWER TRANSMISSION NETWORKS

IRJOLA

1,2

INLAND

OTELER

ANADA

RICHTCHENKO

ANADA

WEDEN

Finnish Meteorological Institute, Helsinki, Finland,

Natural Resources Canada, Ottawa, Canada,

NeuroSpace, Malmö, Sweden, email: risto.pirjola@fmi.fi

Abstract. Geomagnetic storms create a geoelectric field on the ground as described by Faraday’s law of induction.

The geoelectric field drives geomagnetically induced currents (GIC) in technological conductor systems, such as

electric power transmission networks. Generally GIC are a source of problems to the system, which occur due to

saturation of transformers in power grids. GIC can be investigated by measurements or by theoretical modelling. If

the geoelectric field is (assumed to be) known, the computation of GIC in a power system is in principle

straightforward by applying formulas that include the earthing impedance matrix and the network admittance

matrix determined by the network resistances and topology. However, to our experience, some parts of the power

grid data always remain unknown in practice, so sensitivity analyses have to be performed to estimate the effect of

inaccuracies of different quantities on calculated GIC values. GIC can naturally flow everywhere in a galvanically-

connected network, which means, for example, that in autotransformers GIC enter from one voltage level to

another. Therefore autotransformers require special modelling techniques in connection with GIC computations.

Particular care is also needed in the case of two-winding transformers when two (or more) voltage levels are

included in the GIC modelling. In this paper, we discuss all these details appearing in calculations of GIC and

consider our conclusions and solutions.

Introduction

“Space Weather”, which is driven by solar activity,

concerns electromagnetic and particle conditions in the

near-Earth space, e.g. [1]. The consequences of a burst on

the Sun are carried by the solar wind to the Earth, at which

the geomagnetic field interacts with the solar wind.

Finally, this leads to intense and rapidly-varying electric

currents in the Earth’s magnetosphere and ionosphere, i.e.

a space weather storm occurs. The physical processes

associated with space weather are complicated and not yet

fully known, so research must be continued.

Space weather can disturb and even damage

permanently technical equipment in space and on the

ground, which may cause considerable problems to reliable

functioning of the society. The magnetospheric-ionospheric

currents produce a geomagnetic disturbance or storm at the

Earth’s surface. In accordance with Faraday’s law, it

induces a geoelectric field, which drives currents, called

geomagnetically induced currents (GIC), in conductors,

such as electric power transmission networks, oil and gas

pipelines, telecommunication cables and railway circuits. It

is interesting to note that the first GIC observations were

already made much before the beginning of modern space

weather science, i.e. in early telegraph devices in the mid-

1800’s [1,2]. Today, however, power networks, which are

the focus of this paper, constitute the most significant

systems regarding GIC.

In general, GIC, which have typical variation times

from seconds to minutes and hours being thus (quasi-)dc

currents compared to the 50/60 Hz ac frequency, are a

possible source of problems in power networks. The

problems result from half-cycle saturation of

transformers, e.g. [3].

GIC in a network of conductors can be studied by

measurements, e.g. [4], and by model calculations,

which should preferably be verified and adjusted by

recorded GIC data. This paper is concentrated on

theoretical model calculations of GIC in power systems.

Two separate parts can be distinguished when computing

GIC in a power grid (or in any network):

1) Determination of the horizontal geoelectric field

2) Calculation of GIC in the network produced by

the geoelectric field.

The first part is naturally independent of the network

considered. In principle, it requires knowledge of the

Earth’s conductivity structure and of the

magnetospheric-ionospheric currents. The geoelectric

field is then obtained by using Maxwell’s equations and

electromagnetic boundary conditions. In practice,

however, knowledge of space currents is not necessary if

geomagnetic variation data at the Earth’s surface are

available. In this paper, we address the second part and

refer to [5] regarding the first part.

In the next section, the technique applicable to the

second part of a GIC calculation is summarised. It is

followed by sections devoted to possible uncertainties

included in GIC computations and to the need of special

modelling of autotransformers and two-winding

transformers.

Calculation of GIC in a power network

Due to the (quasi-)dc nature of GIC, a dc treatment

can be applied to the determination of GIC driven by the

geoelectric field, i.e. in the second part of a GIC

calculation. For a power network with N stations, we

define an N × N earthing impedance matrix Z

including

527

the earthing resistances of the stations and an N × N

network admittance matrix Y

determined by the

transmission line resistances. By utilising these matrices,

it is possible to derive the following formula for the N ×

1 column matrix I

whose elements are GIC flowing into

(from) the Earth at the stations:

= (1+Y

)

–1

(1)

If the stations are distant enough, making the

influence of GIC at one station on the voltages at other

stations negligible, Z

is diagonal with the elements

equalling the station earthing resistances For additional

details, we refer, for example, to [6,7,8]. In equation (1),

the symbol 1 refers to an N × N unit matrix, and the N ×

1 column matrix J

includes the input from the

geovoltages obtained by integrating the geoelectric field

between the stations. Generally, the geoelectric field is

rotational making the integration path-dependent, and the

geovoltages must be computed along the transmission

lines, e.g. [9,10]. However, it should be noted that a

spatially uniform geoelectric field, which is often

assumed to get an overview of the GIC flow in a

network, is irrotational implying an independence of the

choice of the path in the computation of geovoltages.

Equation (1) shows that if the earthings are perfect, i.e.

= 0, I

and J

are equal.

When applying equation (1) to a three-phase power

network, the three phases are usually, including this

paper, treated as one circuit element, whose resistance is

one third of that of a single phase. Correspondingly, a

GIC value in a circuit element is three times the current

in a single conductor. The (total) earthing resistances of

the stations are often, including this paper, defined to

consist of the actual earthing resistances, of the

transformer resistances, and of any other resistances in

the earthing leads of transformer neutrals with all these

resistances connected in series.

A simple formula for GIC in transmission lines also

exists [6,7]. Regarding scientific and physical

significance, GIC between the network and the Earth and

in the lines are equivalent, but in practice, the former are

more important because they are responsible for the

possible transformer saturation. Moreover, measured

GIC data are usually collected in earthing leads of

transformer neutrals [4].

Inaccuracies in power network data

Besides the horizontal geoelectric field, the

following power network data are needed for the second

part of a GIC calculation [11]:

-Coordinates of the stations

-Total earthing resistances of the stations

-Transmission line resistances

-Network topology and configuration

-Precise information of the connections at the stations

-Information of possible series capacitors

The calculation of GIC from the input data is based

on Ohm’s and Kirchhoff’s laws. Thus, in principle, the

calculation is exact. However, in practice, the geoelectric

field values suffer from approximations, and the power

network data also include inaccuracies and

shortcomings. The latter can be caused by difficulties in

disclosing confidential network information or simply by

insufficient knowledge, and they concern uncertainties in

station locations, unknown resistance values,

approximations when considering autotransformers,

undocumented connections or disconnections of

transmission lines, etc. Consequently the second part of a

GIC calculation remains approximate as well.

It can be shown that uncertainties in earthing

resistance data of even tens of per cent, as well as

inaccuracies of station locations in the kilometre range,

are generally not critical for calculated GIC values in a

power grid [11,12]. This is particularly true if average

values over all sites of the network are considered.

The study presented in [11] indicates that, even

though the overall average impact of a connection or

disconnection of one or two transmission lines on GIC in

a power grid is not large, inadequate knowledge of

connections and disconnections can lead to totally

incorrect calculated GIC values at some sites and thus, in

the worst case, to completely inappropriate

countermeasures for avoiding GIC problems.

Values of possible non-zero off-diagonal elements

of the matrix Z

, which describe the interaction between

the stations of a power network, are not easy to be

determined. Fortunately, both [12] and [13] support that

the effects of non-zero off-diagonal elements on GIC

values are not large. Thus, probably, if necessary, Z

may be regarded as diagonal without getting unusably

erroneous results.

GIC can naturally flow throughout a galvanically-

connected network. Thus, an exact GIC calculation

would require the whole network to be taken into

account. However, the usual situation is that a GIC study

is focussed on a limited area only. It is shown in [14,15]

that GIC do not flow over very long distances in a power

grid. This means that, in a practical study, we need not

extend the network considered far beyond the area of

interest, which, of course, simplifies the calculations.

Although equation (1) looks simple in the particular

matrix form, it includes a lot of parameters coupled together

in complicated ways when a real power network is

considered. Therefore, mathematically precise analytic

investigations of the effects of inaccuracies in power

network data are not possible in practice. The above-

mentioned conclusions of the effects are also based on

numerical studies. The old Finnish 400 kV power network

introduced as a GIC calculation test model in [8] is suitable

for investigating effects of inaccuracies in network data on

GIC values and for testing different GIC calculation

algorithms. It consists of 17 stations and 19 transmission

lines being thus large enough to be realistic but not too large

to unnecessarily complicate GIC computations.

528

Modelling autotransformers and two-

winding transformers

In autotransformers, the higher and lower voltage

networks are in galvanic connection, so the flow of GIC

from one voltage level to another is possible. This means

that even if GIC are only studied in the grid of one

voltage (e.g. 400 kV in Finland or Sweden) the existence

of autotransformers makes the lower voltage grid(s) play

a role, too. If GIC are investigated in a power network

having two (or more) voltage levels then two-winding

transformers must be taken into account as well.

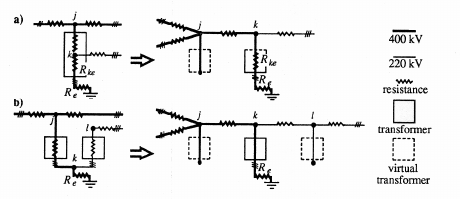
Fig. 1: Modelling of an autotransformer (a)

and a two-winding transformer (b) for GIC

calculations [14,16]. For clarity, one phase of the

three-phase system is only included in the

diagram.

Fig. 1 adopted originally from [16] depicts a

technique for describing an autotransformer and a two-

winding transformer in a manner applicable to the GIC

calculation method governed by equation (1). (Note that,

in order to keep the diagram clear enough, only one

phase is plotted in Fig. 1.) The symbols R

and R

refer

to the resistance of the common lower voltage winding

in an autotransformer and to the actual station earthing

resistance, respectively. In the case of an autotransformer

(a), the high voltage node j becomes a “virtual station”

earthed through an infinite resistance, and the series

winding is treated as a transmission line between

“stations” j and k. In the case of a two-winding

transformer (b), both the high voltage node j and the low

voltage node l become “virtual stations”, and the

windings are regarded as transmission lines between

“stations” j and k and k and l, respectively.

In a modelling of this kind, the “stations” j, k and l

are very near each other, in fact at the same site. Thus,

the earthing impedance matrix Z

would seem to have

non-zero off-diagonal elements. We may conclude the

following values for the elements of Z

that are related to

Fig. 1 [14,16]:

e,jj



e,kk

e,jk

e,kj

(1a – auto) (2)

and

e,jj

e,ll



e,kk

e,jk

e,kj

e,kl

e,lk

e,jl

e,lj

(1b – two-winding) (3)

Looking at Fig. 1b more carefully indicates that,

although the description included in the figure and in

formulas (3) is correct, it is evident that a two-winding

transformer can be modelled in a simpler way by

ignoring the node k and using only “stations” j and l,

which are not connected to each other. Denoting the

winding resistances of the transformers at j and l by R

t,j

and R

t,l

, respectively, the elements of Z

associated with j

and l are

e,jj

t, j

e,ll

t,l

e,jl

e,lj

(4)

Besides theoretical reasoning, we have “proved” this

simplification by numerical calculations as well.

Our recent investigations, based on theoretical

conclusions, numerical computations and considerations

of a simple dc circuit for analogy, indicate the that the off-

diagonal elements of Z

connected with a “virtual station”,

such as j in Fig. 1a and j and l in Fig. 1b do not affect GIC

values in a network. Consequently, referring to equations

(2) and (3), we can replace R

as the value of the off-

diagonal elements with zero (or with any other value).

Concluding remarks

After the geoelectric field is known, GIC in a power

network can in principle be calculated exactly in a

straightforward manner by using dc circuit theory.

However, in practice, approximations are necessary,

which may result, for example, from incomplete power

grid data or from the impossibility of considering the

whole galvanically-connected network where GIC can

flow. In this paper, we summarise some rules of thumb

necessary to be kept in mind when making

approximations in GIC calculations. Special attention is

paid to the modelling of autotransformers and two-

winding transformers.

Information about the authors

Dr Risto Pirjola (FMI & NRCan) and Dr David

Boteler (NRCan) have carried out scientific research on

GIC and geoelectromagnetics for more than 30 years. Dr

Larisa Trichtchenko joined NRCan in the 1990’s. Her

scientific interests include space weather forecasting,

magnetospheric physics and GIC. Dr Magnus Wik runs

his own company NeuroSpace since 2009, whose

activities concern space weather, GIC and solar

phenomena.

References

1. L. J. Lanzerotti, D. J. Thomson, and C. G.

Maclennan, “Engineering issues in space weather,”

529

Modern Radio Science 1999, M. A. Stuchly (ed.),

International Union of Radio Science (URSI), Oxford

University Press, pp. 25-50, 1999.

2. D. H. Boteler, R. J. Pirjola, and H.

Nevanlinna, “The effects of geomagnetic disturbances on

electrical systems at the Earth’s surface,” Adv. Space

Res., Vol. 22, pp. 17-27, 1998.

3. J. G. Kappenman, “Geomagnetic

Disturbances and Impacts upon Power System

Operation,” The Electric Power Engineering Handbook,

2nd Edition, edited by L. L. Grigsby, CRC Press/IEEE

Press, Chapter 16, pp. 16-1 - 16-22, 2007.

4. A. T. Viljanen, R. J. Pirjola, K. M. Pajunpää,

and A. A. Pulkkinen, “Measurements of geomagnetically

induced currents by using two magnetometers,”

Proceedings of the 8-th International Symposium on

Electromagnetic Compatibility and Electromagnetic

Ecology, Saint-Petersburg, Russia, June 16–19, 2009, pp.

227-230, 2009.

5. A. Viljanen, A. Pulkkinen, O. Amm, R.

Pirjola, T. Korja, and BEAR Working Group, “Fast

computation of the geoelectric field using the method of

elementary current systems and planar Earth models,”

Ann. Geophys., Vol. 22, No. 1, pp. 101-113, 2004.

6. M. Lehtinen, and R. Pirjola, “Currents

produced in earthed conductor networks by

geomagnetically-induced electric fields,” Ann. Geophys.,

Vol. 3, No. 4, pp. 479-484, 1985.

7. R. Pirjola, “Calculation of geomagnetically

induced currents (GIC) in a high-voltage electric power

transmission system and estimation of effects of

overhead shield wires on GIC modelling,” J. Atmos. Sol.

Terr. Phys., Vol. 69, Issue 12, pp. 1305-1311, 2007.

8. R. J. Pirjola, “Properties of matrices included

in the calculation of geomagnetically induced currents

(GICs) in power systems and introduction of a test model

for GIC computation algorithms,” Earth, Planets and

Space, Vol. 61, No. 2, pp. 263-272, 2009.

9. D. H. Boteler, and R. J. Pirjola, “Modelling

Geomagnetically Induced Currents produced by Realistic

and Uniform Electric Fields,” IEEE Transactions on

Power Delivery, Vol. 13, No. 4, pp. 1303-1308, 1998.

10. R. Pirjola, “Geomagnetically Induced

Currents During Magnetic Storms,” IEEE Transactions

on Plasma Science, Vol. 28, No. 6, pp. 1867-1873, 2000.

11. R. J. Pirjola, “Effects of inaccuracies in

power network data on calculations of geomagnetically

induced currents,” Proceedings of the 8-th International

Symposium on Electromagnetic Compatibility and

Electromagnetic Ecology, Saint-Petersburg, Russia, June

16–19, 2009, pp. 231-234, 2009.

12. R. Pirjola, “Study of effects of changes of

earthing resistances on geomagnetically induced currents

in an electric power transmission system,” Radio

Science, Vol. 43, No. 1, RS1004, doi:

10.1029/2007RS003704, 13 pp., 2008.

13. R. Pirjola, “Effects of interactions between

stations on the calculation of geomagnetically induced

currents in an electric power transmission system,”

Earth, Planets and Space, Vol. 60, No. 7, pp. 743-751,

2008.

14. R. Pirjola, “Effects of space weather on high-

latitude ground systems,” Adv. Space Res., Vol. 36, Issue

12, doi: 10.1016/j.asr.2003.04.074, pp. 2231-2240, 2005.

15. R. J. Pirjola, “On the flow of geomagnetically

induced currents in an electric power transmission

network,” Canadian Journal of Physics, Vol. 88, No. 5,

pp. 357-363, 2010.

16. T. Mäkinen, “Geomagnetically induced

currents in the Finnish power transmission system,”

Finnish Meteorological Institute, Geophysical

Publications, No. 32, Helsinki, Finland, 101 pp., 1993.

530

RESPONSES OF POWER SYSTEMS TO THE NATURAL GEOMAGNETIC

VARIATIONS AT DIFFERENT LATITUDES

RICHTCHENKO

OLT

1,2

IRJOLA

1,3

CANADA

Geomagnetic Laboratory, Natural Resources Canada, e-mail: ltrichtc@nrcan.gc.ca;

University of Waterloo, Canada,

Finnish Meteorological Institute, Finland

Abstract. Impacts of the natural low-frequency electromagnetic fluctuations (geomagnetic storms) on power

grids can be significant enough to cause equipment damage or even power blackouts. In order to prevent

these damaging impacts, the effective procedures should be placed based on the assessments of the geomag-

netically induced currents (GIC) in power grids and their interference with the essential equipment.

The GIC sizes are influenced by the amplitude of the geomagnetic field variations, ground conductivity

structure, and topology and characteristics of the affected network. Also, it is anticipated that the northern

networks would experience larger GICs due to their location in the auroral zone, where the rate of occur-

rence of the geomagnetic storms is larger. It will be shown that the network configuration plays its role in

the GIC distribution over the power grid and proper network modelling is important component for the as-

sessment of the geomagnetic hazard to power grids.

Introduction

Importance of the safety and security of electricity

supplies in modern world is hard to overestimate. Sev-

eral high-level documents and presentations emphasizing

the role of assessment and mitigation of the negative

impacts of geomagnetic storms on critical technology

have appeared almost simultaneously at the high gov-

ernmental levels in North America, UK and EU

[1, 2].

Thus, socio-economic consequences of the vulner-

ability of the power grids to the geomagnetic storms

make the GIC-research of primary importance, espe-

cially in the view of the upcoming increase in solar ac-

tivity and, thus, increase in the possibilities to have more

geomagnetic storms.

In this paper we describe the general methodology

for assessment of GIC effects on power grids and give

more detailed estimations of the importance of each step

in GIC modelling. As examples, we use GIC data and

modelling results for North American power grids lo-

cated at different latitudes.

GIC Assessment

In power systems, geomagnetically induced currents

(GIC) flow through the transformer windings at

transformer substations, producing extra magnetisation

which can saturate the core of the transformers causing

increased harmonics. This results in transformer heating,

malfunctioning of relays and other equipment on the

system and leads to problems ranging from trip-outs of

individual lines to collapse of the whole system.

The amplitude of the GIC variations due to

geomagnetic interference depends on: (1) the geoelectric

field which drives GIC in power grids, and (2) the details

of the power network (resistance to ground, topology,

orientation, number of transformers at each substation

and their types). Thus, in order to properly assess the

possible damage from geomagnetic hazards, detailed

modeling of the system is needed.

Modelling of the GIC is usually supported and

verified by GIC data measured in several key points of

the system.

The first part of the modelling is to define the

geoelectric fields in the ground. Unfortunately, there are

no regular recordings of this field and therefore,

modelling of the geoelectric field using the closest to the

power grid geomagnetic field observations together with

models of the Earth surface inpedance is widely used in

geophysics, magnetotelluric applications and for GIC

modelling [3-5].

We use the geomagnetic coordinate system with axis

x north, y east, and z vertically downwards. For the fre-

quency range of 1sec to 24 hours and earth resistivity

range 1 to1000 Ohm-m, displacement currents are small

in comparison with conductivity currents. Therefore,

electric and magnetic fields in the frequency domain can

be given by the diffusion equations [3]. For our case,

when the magnetic field at the surface of the earth (1st

layer) is known from the magnetic observations, the

electric field (E

surface

) can be obtained from (1.. Here the

surface impedance (Z

surface

) is the ratio of magnetic (H)

and electric fields mesured during magnetotelluric

surveys or inferred from a literature review [6].

surfacesurfacesurface

HZE =

(1)

The impedance at any layer

can be found by apply-

ing the recursion relation for the impedance of an

- lay-

ered half-space [5].

( )

)2(













−

erk

ωµ

where

are the thickness and propagation con-

stant

ωµσ

ik =

of the layer

, in case of the surface

impedance the layer number is

=1 ;

is the reflection

coefficient at each layer and can be obtained from