Работа выполнена в Microsoft Office Excel по учебнику "Практикум по
эконометрике" Елисеева И. И., ( 2 страницы).
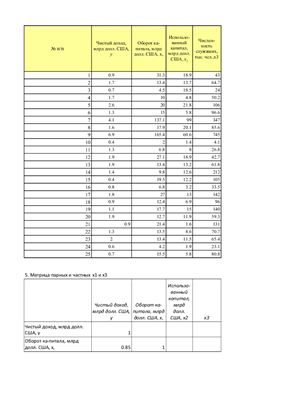
Задание на странице 1:
Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения и показателей тесноты связи проверьте с помощью F-критерия.
Оцените качество уравнения через среднюю ошибку аппроксимации.
Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе и по t-критерию для коэффициентов регрессии отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а — 0,10).
Задание на странице 2 выполнено по задаче 23, но с применением логарифмического анализа.
Задание на странице 1:
Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения и показателей тесноты связи проверьте с помощью F-критерия.
Оцените качество уравнения через среднюю ошибку аппроксимации.
Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе и по t-критерию для коэффициентов регрессии отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а — 0,10).
Задание на странице 2 выполнено по задаче 23, но с применением логарифмического анализа.