Женко Л.А. (сост.). Разработка системы передачи информации с временным уплотнением линиий связи (ВУЛС)
Подождите немного. Документ загружается.


11
3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ
НА ВХОДЕ КОММУТАТОРА
Изобразить по аналогии с рис.3.1 отрезок реализации случайного процесса (СП),
найти среднее значение, дисперсию, рассчитать и построить нормированную
R(
τ
)
автокорреляционную функцию (АКФ) центрированного СП, построить функцию
распределения и гистограмму распределения мгновенных значений процесса
(вероятность попадания значений СП в каждый интервал). По гистограмме дать
заключение о законе распределения процесса: равномерный, нормальный, близкий к
гармоническому колебанию. Анализируя
R(
τ
), дайте заключение о наличии
периодической составляющей СП, определите интервал корреляции
Δτ
и интервал
дискретизации по критерию Железнова Н.А.
Δ
t<
Δτ
.
Δ
P(x)
F(x)
0,03 1,00
0,08 0,97
0,18 0,89
0,24 0,71
0,15 0,47
0,15 0,32
0,12 0,17
0,05 0,05
t, mc
Рис.3.1
Примечание: Процесс должен попадать во все уровни. Старайтесь изобразить
процесс как можно "случайнее". На рисунке не должно быть участков, когда следствие
происходит раньше причины (показано пунктиром на 16 мс). При построении функции
распределения
f(х)=Р(Х<х) и гистограммы
Δ
Р(х) нужно учитывать, что вероятность
попадания СП в данный уровень пропорциональна времени пребывания процесса в этом
уровне. Например, принимая за 100% (Р=1) общее время отрезка реализации 100
мм, в
первом снизу уровне оказалось 5 мм. Это 5%
или 0,05. Таким образом, вероятность
попадания процесса в этот уровень Р
1
= 0,05. Для того чтобы найти Р
2
, нужно определить
вероятность попадания в два верхних уровня, т.е. Р
1+2
= 0,17. Отсюда, во втором снизу
уровне
ΔР
2
= 0,12 и т.д. Справа от графика на рис.3.1 показаны две колонки цифр: левая -
вероятность нарастающим итогом, правая - вероятность попадания мгновенных значений
в данный интервал. Соответственно по правой колонке строится F(
х), по левой –
гистограмма
ΔР(х).
Для нахождения среднего значения (постоянной составляющей)
x
на отрезке
реализации надо взять 20 отсчетов через интервал
Δt . Для простоты расчетов значение
отсчета можно брать целым числом, если отсчет меньше половины кванта, принимается
нижний уровень, больше - верхний. Расчет
x
можно производить по двум формулам
∑
=
n
i
x
n
x
1
1
и
∑
=
n
ii
xPx
1
, результаты должны быть одинаковыми, в этом случае процесс
можно считать эргодическим.
При определении К(
τ
) и R(
τ
) следует учитывать, что
x
и D получены путем
усреднения 20 значений процесса. При расчете К(
τ
) нам придется пользоваться только

12
10 точками, т.к. при К(
Δ
t
⋅
10) будут задействованы все значения процесса
∑
−⋅−=⋅Δ=
+
10
1
10
)()(
10
1
)10()( xxxxtKK
ii
τ
.
Из-за малой длины реализации нет уверенности в стационарности процесса, поэтому
x
и D могут быть разными в начале и в конце реализации. Для R(
τ
) возможно получение
результатов по формуле
)0(
)(
)(
K
K
ctR
τ
=⋅Δ
, с = 0,1,3,…10,
где R(
τ
) =
)( ctR ⋅Δ
центрированное и нормированное значение АКФ;
К(
τ
) - ненормированная автокорреляционная функция центрированного процесса.
4. ЭНТРОПИЯ ДИСКРЕТНОГО ИСТОЧНИКА. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
Задать последовательность двоичных символов в соответствии с вероятностями
табл.4.1. Определить энтропию источника, пропускную способность канала, считая, что
τ
0
- длительность символа получена в пункте 2. Закодировать последовательность
группами из двух элементов статистическим кодом, определить скорость передачи
информации R
и
и пропускную способность канала С
К
. Закодировать последовательность
группами из трех элементов и также определить скорость передачи информации и
пропускную способность канала. Показать, что при кодировании группами из большего
числа элементов скорость передачи информации R
и
стремится к пропускной способности
канала. Сравнить коэффициенты использования канала при трех способах кодирования.
Пропускная способность канала
T
H
C
m
K
= ,здесь Н
m
-максимальная энтропия
источника,
Т - средняя продолжительность кодовой комбинации. Для бинарного
(двоичного) источника
Н
m
=1
бит
/символ, Т =τ
0
, С
К
=1/τ
0
бит
/с.
Скорость передачи информации определяется реальной энтропией источника, а т.к.
Н
аi
< Н
m
, R
и
= Н
аi
/τ
0
< С
К
.
Считается, что если
R
и
< С
К
, источник не согласован с каналом. При отсутствии
помех такое согласование можно осуществить с помощью статистического кодирования.
Составим группы из двух элементов: 00, 01, 10, 11. Определим вероятности этих
сообщений и с помощью методики Фэно закодируем эти сообщения статистическим
кодом. Определим энтропию источника и среднюю длину кодовой комбинации
n .
Пропускная способность канала будет реализована только при
Н
аi
= n . Но т.к. n > Н
аi
R
и
= Н
аi
/
n
⋅τ
0
< С
К
=1/τ
0
.
Посмотрим, получим ли
мы лучшее согласование источника с каналом при
группировке из трех элементов. Действуя аналогично, вновь получим
Н
аi
и n уже для
источника восьми сообщений: 000, 001, 010, 011, 100, 101, 110, 111. Выполнив расчеты,
убеждаемся, что коэффициент использования канала увеличился:
1→=
n
H
C
R
i
а
K
и
.
Чтобы получить еще лучшее согласование источника с каналом, необходимо
дальнейшее укрупнение сообщений. Ясно, что это усложнит технику кодирования.
Таким образом, получено практическое доказательство первой теоремы Шеннона о
кодировании.

13
Таблица 4.1
Вариант P(I) P(0) P(I'/I), P (I'/0)
1 0,05 0,98 0,03
2 0,08 0,97 0,04
3 0,11 0,96 0,05
4 0,12 0,95 0,06
5 0,92 0,94 0,07
6 0,93 0,98 0,08
7 0,94 0,97 0,09
8 0,95 0,96 0,02
9 0,13 0,95 0,03
10 0,07 0,94 0,04
11 0,08 0,99 0,99 0,05
12 0,98 0,91 0,09
13 0,92 0,08
14 0,21 0,91 0,1
15 0,18 0,97 0,06
16 0,22 0,89 0,01
17 0,81 0,99 0,07
18 0,1 0,92 0,05
19 0,12 0,93 0,06
20 0,94 0,98 0,02
21 0,91 0,97 0,02
22 0,09 0,89 0,02
23 0,12 0,96 0,04
24 0,13 0,91 0,06
25 0,09 0,93 0,09
5. ДВОИЧНЫЙ КАНАЛ. ИССЛЕДОВАНИЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
Задан двоичный канал: априорные вероятности передачи символов Р(0) или Р(1),
вероятности переходов P(I'/I), P (I'/0).
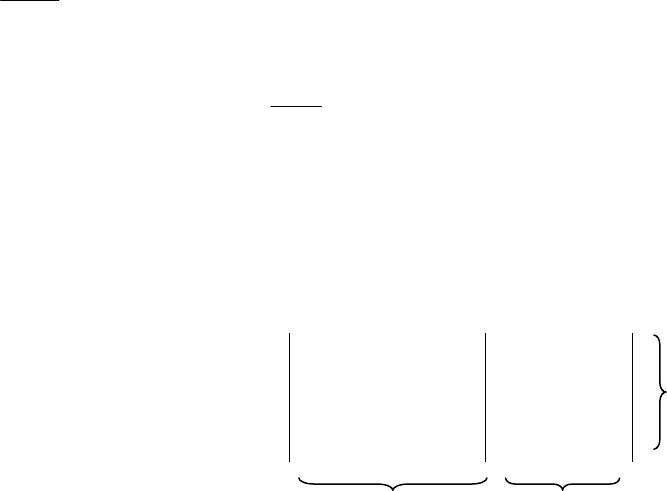
Изобразить граф переходов, подсчитав все необходимые вероятности, в том числе
среднюю вероятность ошибки в канале Р(0) , вероятности приема символов P(0') и P (I').
Считая, что принят менее вероятный символ, дать заключение о переданном символе.
Дать краткую характеристику канала (симметричный, с памятью, со стиранием). По
средней вероятности ошибки в канале определить вероятность однократной, двукратной
и трехкратной ошибок в кодовой комбинации длиной
n (n взять из табл.2.1). Данные для
различных вариантов приведены в табл.4.1.
При выполнении задания пользуйтесь /1/,/2/ стр.40, /2/ стр.89. Подробно
комментируйте действия, указывая, например, какие вероятности образуют полную
группу событий, дайте физическое обоснование несимметричности или симметричности
канала, памяти и т.п. Где это необходимо, приводите соответствующие графики,
14
например, зависимость вероятности ошибки от ее кратности.
6
. КОРРЕКТИРУЩЕЕ КОДИРОВАНИЕ
Считая, что число информационных символов
к задано в табл. 2.1, построить
корректирующий код Хемминга для защиты комбинаций от одиночной ошибки.
Для этого составить образующую и проверочную матрицы, получить уравнения
кодирования и декодирования и по ним соответствующие структурные схемы. Ввести в
схему кодирования информационную безызбыточную комбинацию и получить
проверочные символы. Подав на вход схемы декодирования полученную кодовую
комбинацию,
проверить схему декодирования на работоспособность. Ввести ошибку в
один из информационных символов, проверить работу схемы декодирования по
исправлению ошибок.
Определить относительное число обнаруживаемых и необнаруживаемых ошибок.
При выполнении упражнения лучше всего пользоваться /4, стр.69 и далее/.
Познакомиться с материалом, изложенным в основном учебнике по дисциплине /3,
стр.272 и далее/. В /I/ этого материала практически
нет.
Построение корректирующих (исправляющих) кодов связано с введением
избыточности. Так, блок из
к информационных символов должен быть дополнен n-к
символами (проверочными). Символы
n и к связаны следующим неравенством
Е
n
к
+
≤
1
2
2, называемым иногда «границей Хемминга», Е - общее число возможных
ошибок в кодовой комбинации длиной п исправляемой кратности. Для исправления
однократной ошибки
n
n
к
+
≤
1
2
2 или
n
кn
≥
−
−
12 .
Корректирующий код обычно задается образующей А и проверочной Н матрицами,
однако, для выполнения задания достаточно построения проверочной матрицы.
Классическая матрица должна иметь n-к строк, n столбцов, причем последние n-к
столбцов должны представлять собой единичную матрицу, а первые к столбцов могут
быть в виде инвертированной единичной матрицы:
a
1
a
2
a
3
a
4
a
5
a
6
a
7
0 1 1 1 1 0 0
1 0 1 1 0 1 0
1 1 0 1 0 0 1
H=
к
n-к
n-к
Элементы матрицы обозначаются a
i
. Проверочными символами для кода Хемминга
будут a
5
, a
6
, a
7
. Эти символы могут быть получены из информационных с помощью
уравнений кодирования:
а
5
= a
2
⊕ a
3
⊕ a
4
, а
6
= a
1
⊕ a
3
⊕ a
4
, а
7
= a
1
⊕ a
2
⊕ a
4.
Для получения каждого проверочного символа суммируются по модулю 2 символы
кодовой комбинации, которые стоят на i месте в кодовой комбинации. Пример: пусть
задана безызбыточная комбинация
a
1
a
2
a
3
a
4
1 0 1 1
15
Тогда а
5
= 0 ⊕ 1
⊕ 1=0, а
6
= 1 ⊕ 1
⊕ 1=1, а
7
= 1 ⊕ 0
⊕ 1.
Получена кодовая комбинация из семи символов:
информационные 1011 010
проверочные.
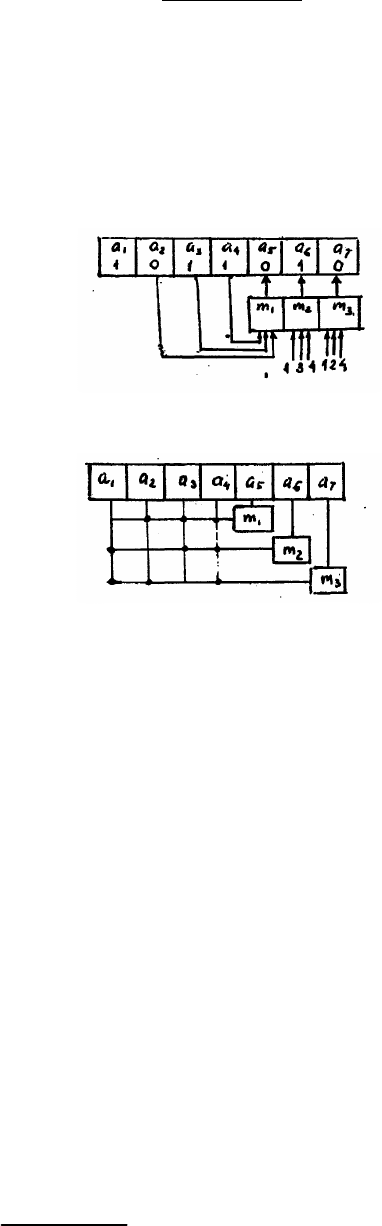
Схема кодирования представляет собой n триггеров, в первые к из которых вводят
информационные символы, на входы п-к (последних) триггеров подключены выходы
сумматоров по модулю 2 m
i
, входы которых в соответствии с уравнениями кодирования
подключены к выходам информационных триггеров (см.рис.6.1).
Для простоты изображения и наглядности схема кодирования может быть
изображена структурно (см.рис.6.2).
Рис.6.1
Рис.6.2
Полученный код является параллельным. При передаче символы поочередно
"выталкиваются" в линию связи с помощью тактового генератора.
Декодирование осуществляется с помощью п-к уравнений проверок:
r
1
= a
2
⊕ a
3
⊕ a
4
⊕ a
5
,
r
2
= a
1
⊕ a
3
⊕ a
4
⊕ a
6
,
r
3
= a
1
⊕ a
2
⊕ a
4
⊕ a
7
.
Видно, что для получения каждого уравнения суммируются по МОД2 символы,
стоящие в соответствующей строке матрицы Н в виде единиц. При правильно принятой
комбинации результаты проверок должны дать r
i
= 0 (осуществляется проверка на
четность). Проверяем полученную ранее комбинацию: r
1
= 0 ⊕ 1
⊕ 1⊕0, r
2
= 1 ⊕ 1
⊕ 1⊕1,
r
3
= 1 ⊕ 0
⊕ 1⊕ 0. Анализируя уравнения, видим, что в каждом участвуют не все
символы. Так, если r
1
= 0, то a
1
, a
2
, a
3
, a
4
, a
5
приняты без ошибок. Если при этом r
2
= 1;
r
3
= 1, то символ a
1
принят с ошибкой (вместо 1 принят 0). Рассмотрим все возможные
результаты суммирования:
r
1
= 0 1 1 1
r
2
= 1 0 1 1
r
3
= 1 1 0 1.
Ошибка в символе a
1
, a
2
, a
3
, a
4
.
Проверяются только информационные символы, а проверочные после декодирования
уже не нужны.
В упрощенной структурной схеме показано и автоматическое исправление ошибки.
Для этого выходы сумматоров с помощью четырех схем 3И распределяются на четыре
выхода, выход каждой схемы 3И соединен с соответствующим информационным
триггером. Появление на выходе 3И единицы изменит символ в
соответствующем

16
n
триггере на противоположный.
Рис.6.3
На схеме ⊕ обозначает инверсный выход сумматора. Ниже показана схема
включения m
i
и 3И .
Рис.6.4
Существует также другой систематический код Хемминга, где матрица состоит из
n
строк и n-к столбцов, каждая строка - двоичный номер символа (или триггера):
п-к
a
1
0 0 0 1
a
2
0 0 1 0
a
3
0 0 1 1
a
4
0 1 0 0
a
5
0 1 0 1
a
6
0 1 1 0
a
7
0 1 1 1
Проверочные символы - в триггерах 1, 2, 4, 8... и т.д., т.е. в тех, номера которых
имеют только одну единицу в строке, причем эта единица начинает собой
соответствующий столбец.
Получение уравнений кодирования осуществляется суммированием по столбцам тех
элементов кодовой комбинации, которые в данной матрице обозначены единицей.
Аналогично получаем уравнения декодирования, причем результат проверки
дает
двоичный номер искаженного ошибкой разряда.
При корректирующем кодировании всего может быть образовано 2
n
комбинаций, из
них 2
к
называются разрешенными, а 2
n
- 2
к
- запрещенными. Если в результате ошибки
одна разрешенная комбинация перешла в другую разрешенную, эта ошибка не может
быть обнаружена. Обнаруживаются таким образом только те ошибки, которые переводят
разрешенную кодовую комбинацию в запрещенную. Отсюда относительное число
(вероятность) обнаруживаемых ошибок
n
к
n
кn
2
2
1
2
22
−=
−
, а
n
к
2
2
- необнаруживаемых. Эти
вероятности образуют полную группу событий.

17
7.
ИСПОЛЬЗОВАНИЕ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ ОБНАРУЖЕНИЯ
И РАСПОЗНАВАНИЯ ПРИ ОПРЕДЕЛЕНИИ ОШИБКИ В ДЕМОДУЛЯТОРЕ
Определить вероятность ошибки в решающей схеме РC-I (дискретном
демодуляторе), выбрав статистический критерий обнаружения и распознавания, если
вероятности символов заданы в табл. 4.1. Сигнал, соответствующий символу 1 -
гармоническое колебание, в канале действует нормальная помеха,
n
c
P
P
h =
2
, а отсчет
производится по амплитудному значению. Параметры сигнала указаны в табл.7.1.
Таблица 7.1
h
2
4 5 6 7 8
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
Варианты
5 10 15 20 25
При выполнении этого задания лучше всего пользоваться учебным пособием по
теоретическим основам транспортной связи /1/ или конспектом лекций. При отсутствии
и того и другого приводятся краткие сведения по данному разделу.
Предполагается, что канал стационарен, т.е. помеха в непрерывном канале также
стационарна и распределена по нормальному закону. Канал без памяти, т.
е. вероятности
переходов одного символа в другой не зависят от того, какой символ передавался до
этого.
Существует большое число статистических критериев, по которым строится PC-I.
Все они связаны с выбором порогового уровня между значениями сигнала,
соответствующего символам 1 и 0. Естественно, потребитель информации должен
стремиться к
минимуму потерь, но эти потери можно минимизировать только тогда,
когда сведения об источнике информации наиболее полны. Если известны только
символы алфавита, уровни сигнала и помехи, например,
n
c
P
P
h =
2
или V
m
и σ, то можно
пользоваться только критерием максимального правдоподобия, при котором пороговый
уровень проводится посредине расстояния между сигналами, соответствующим 1 и 0.
2
d
U
пор
= расстояние d при AT (амплитудной телеграфии) определяется d=1.
При ЧТ
d= 2, т.к. сигналы ортогональны. При ФТ d=2, т.к. сигналы
противоположны.
Нужно уметь рисовать в масштабе графики распределений условных вероятностей
приема сигнала
х, если передан 0 – f(х/o) и если передана 1 – f(х/1). Т.к. помеха
нормальна, а полный размах нормального процесса равен 6
σ (пусть σ=1, h=3, h
2
=9, где h
– превышение сигнала над помехой), то график АТ будет выглядеть следующим
образом:

18
и
пор
= d/2=h/2
d = h
«1»
«0»
Рис.7.1
Тот же график для ФГ будет:
«1»
«0»
d = 2h
и
пор
=h
Рис.7.2
График для ЧТ будет промежуточным.
Вероятность ошибки первого рода
α - ложная тревога (символ принят, на самом деле
его нет) равна ошибке второго рода
β -пропуск цели (символ не принят, хотя он есть). По
первому графику
α и β весьма велики, около 0,05. Определим их расчетами: определим
относительное превышение порогового уровня над помехой
h/2 (аргумент функции
Крампа, см. приложение 2):
5,1
2
3
)( ==Фu; Ф(и)= 0,4332,
отсюда
Р
0
=
α
=
β
=0,5- Ф(и)=0,5-0,4332=0,0668.
Во втором случае на графике ошибки не заметны, но графики вероятностей
перекрываются.
3
2
2
6
)( ===
σ
m
пор
U
u
Фu; Ф
1
(и)= 0,9973; Р
0
=0,0013.
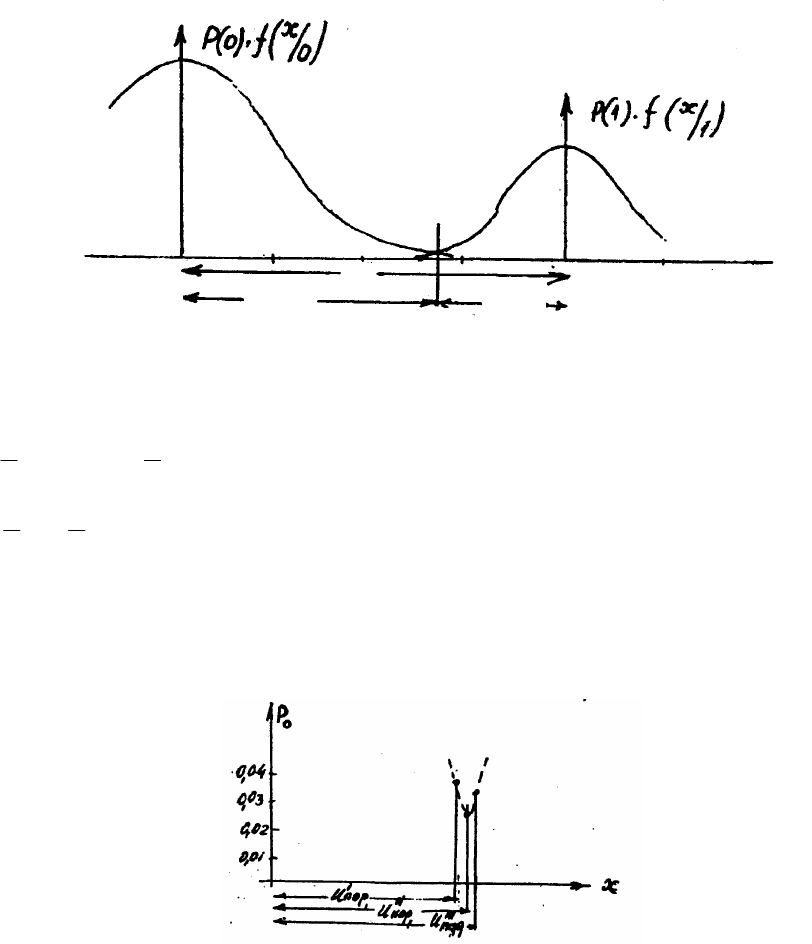
Когда что-либо о принятых сигналах известно заранее, результат можно улучшить. У
нас известно, что символы передаются с разными вероятностями, это надо использовать.
Перестраиваем графики с учетом "веса" символов.
Пусть Р(0)=0,9
, тогда Р(1)=0,1.
Площади под кривыми с учетом веса относятся друг к другу, как 9/1, соответственно
линейные размеры как 3/1 (см. рис.7.3).
Пороговый уровень проводим через точки пересечения графиков, но точных
значений
u
пор1
и u
пор2
мы заранее не знаем.
19
d
и
′
по
р
1
и
′
по
р
2
и
пор
«1»
«0»
Рис.7.3
Пусть пороговый уровень
u
пор
делит расстояние d (d=h) на части в отношении 3/1.
hu
пор
4
3
1
=
′
; 25,2
4
9
)( ==Фu; Ф
1
(и)
≈
0,4877;
α
=0,5(1-0,4877)=0,012;
75,0
4
3
4
1
2
===
′
hu
пор
; Ф
2
(и)
≈
0,2734;
β
=0,5-0,2734=0,2266; Р
0
=
α⋅
0,9+
β⋅
0,1=0,035.
Эта величина оказалась меньше, чем при первом критерии для AT (0,066).
Изменяя положение порогового уровня, можно попытаться еще уменьшить
Р
0
→Р
0 min
.
Построить график зависимости
Р
0
от u
пор
:
Рис.7.4
8. СПЕКТРЫ СИГНАЛОВ В ЛИНИИ СВЯЗИ
Изобразить временную и частотную диаграммы последовательности видеоимпульсов
и радиоимпульсов, если параметры последовательности заданы в табл.8.1.
При выполнении данного упражнения сначала выбирают форму импульсов. Чаще
всего в технике используются импульсы прямоугольной формы. Спектральная функция
этих импульсов имеет вид
sin x/x.
Затем по заданным параметрам определяем остальные. Так, если известен период
следования импульсов Т
0
, то можно определить частоту первой гармоники f
1
, а если
известна скважность
Q, то и длительность импульса
τ
. Если известна длительность
импульса и число периодов колебаний несущей
S, укладывающихся в длительности
τ
,
можно определить частоту несущей
f
н
. Через длительность импульса
τ
определяют также
ширину лепестка спектра
f
л
. Прежде чем изображать требуемые диаграммы, нужно
обязательно рассчитать все параметры этих диаграмм и привести формулы, по которым

20
эти параметры получены. На диаграммах должен быть указан масштаб (мс или кГц),
начало координат, характерные точки (особенно для спектра).
Вспомните,
чем отличаются спектры видео- и радиоимпульсов и в чем их сходство.
Таблица 8.1
Вариант
Т
0
, мс
τ
, мс
Q
S
f
н
, кГц f
л
, кГц
1 1 4 1
2 0,5 5 10
3 0,2 5 2
4 0,5 50 10
5 0,2 4 25
6 0,1 10 50
7 0,05 5 100
8 1 1 4
9 0,5 , 2 10
10 0,2 4 20
11 0,1 10 5
12 1 4 5
13 0,2 5 20
14 0,1 4 20
15 10 40
16 5 1 1
17 0,8 2 5
18 0,5 4 10
19 0,1 5 50
20 0,05 0,01 4
21 1 2 5
22 0,2 4 4
23 5 3 10
24 0,05 4 2
25 0,25 10 1
