Задачи и решения 44й международной математической олимпиады (Токио, 2003)
Подождите немного. Документ загружается.

33
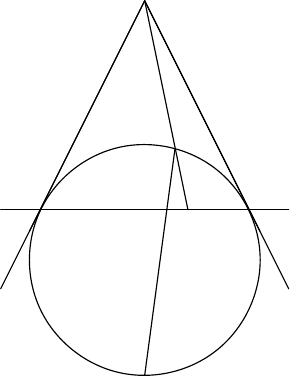
G2. Three distinct points A, B, C are fixed on a line in this order. Let Γ be a circle passing
through A and C whose centre does not lie on the line AC. Denote by P the intersection
of the tangents to Γ at A and C. Suppose Γ meets the segment P B at Q. Prove that the
intersection of the bisector of ∠AQC and the line AC does not depend on the choice of Γ.
Solution 1.
C
P
A
Q
S
B
R
Γ
Suppose that the bisector of ∠AQC intersects the line AC and the circle Γ at R and S,
respectively, where S is not equal to Q.
Since 4AP C is an isosceles triangle, we have AB : BC = sin ∠AP B : sin ∠CP B.
Likewise, since 4ASC is an isosceles triangle, we have AR : RC = sin ∠ASQ : sin ∠CSQ.
Applying the sine version of Ceva’s theorem to the triangle P AC and Q, we obtain
sin ∠AP B : sin ∠CP B = sin ∠P AQ sin ∠QCA : sin ∠P CQ sin ∠QAC.
The tangent theorem shows that ∠P AQ = ∠ASQ = ∠QCA and ∠P CQ = ∠CSQ =
∠QAC.
Hence AB : BC = AR
2
: RC
2
, and so R does not depend on Γ.

34
Solution 2.
A
Q
B
R
y
x
O
(0, −p)
M
¡
0, −p −
p
1 + p
2
¢
C(1, 0)
P (0, 1/p)
Γ
Let R be the intersection of the bisector of the angle AQC and the line AC.
We may assume that A(−1, 0), B(b, 0), C(1, 0), and Γ : x
2
+ (y + p)
2
= 1 + p
2
. Then
P (0, 1/p).
Let M be the midpoint of the largest arc AC. Then M
¡
0, −p −
p
1 + p
2
¢
. The points
Q, R, M are collinear, since ∠AQR = ∠CQR.
Because P B : y = −x/pb + 1/p, computation shows that
Q
µ
(1 + p
2
)b − pb
p
(1 + p
2
)(1 − b
2
)
1 + p
2
b
2
,
−p(1 − b
2
) +
p
(1 + p
2
)(1 − b
2
)
1 + p
2
b
2
¶
,
so we have
QP
BQ
=
p
1 + p
2
p
√
1 − b
2
.
Since
MO
P M
=
p +
p
1 + p
2
1
p
+ p +
p
1 + p
2
=
p
p
1 + p
2
,
we obtain
OR
RB
=
MO
P M
·
QP
BQ
=
p
p
1 + p
2
·
p
1 + p
2
p
√
1 − b
2
=
1
√
1 − b
2
.
Therefore R does not depend on p or Γ.

35
G3. Let ABC be a triangle and let P be a point in its interior. Denote by D, E, F the
feet of the perpendiculars from P to the lines BC, CA, AB, respectively. Suppose that
AP
2
+ P D
2
= BP
2
+ P E
2
= CP
2
+ P F
2
.
Denote by I
A
, I
B
, I
C
the excentres of the triangle ABC. Prove that P is the circumcentre
of the triangle I
A
I
B
I
C
.
Solution. Since the given condition implies
0 = (BP
2
+ P E
2
) − (CP
2
+ P F
2
) = (BP
2
− P F
2
) − (CP
2
− P E
2
) = BF
2
− CE
2
,
we may put x = BF = CE. Similarly we may put y = CD = AF and z = AE = BD.
If one of three points D, E, F does not lie on the sides of the triangle ABC, then this
contradicts the triangle inequality. Indeed, if, for example, B, C, D lie in this order, we have
AB + BC = (x + y) + (z − y) = x + z = AC, a contradiction. Thus all three points lie on
the sides of the triangle ABC.
Putting a = BC, b = CA, c = AB and s = (a + b + c)/2, we have x = s − a, y = s − b,
z = s − c. Since BD = s − c and CD = s − b, we see that D is the point at which the
excircle of the triangle ABC opposite to A meets BC. Similarly E and F are the points at
which the excircle opposite to B and C meet CA and AB, respectively. Since both P D and
I
A
D are perpendicular to BC, the three points P, D, I
A
are collinear. Analogously P , E,
I
B
are collinear and P , F , I
C
are collinear.
The three points I
A
, C, I
B
are collinear and the triangle P I
A
I
B
is isosceles because
∠P I
A
C = ∠P I
B
C = ∠C/2. Likewise we have P I
A
= P I
C
and so P I
A
= P I
B
= P I
C
. Thus
P is the circumcentre of the triangle I
A
I
B
I
C
.
Comment 1. The conclusion is true even if the point P lies outside the triangle ABC.
Comment 2. In fact, the common value of AP
2
+ P D
2
, BP
2
+ P E
2
, CP
2
+ P F
2
is equal
to 8R
2
−s
2
, where R is the circumradius of the triangle ABC and s = (BC + CA + AB)/2.
We can prove this as follows:
Observe that the circumradius of the triangle I
A
I
B
I
C
is equal to 2R since its orthic
triangle is ABC. It follows that P D = P I
A
−D I
A
= 2R −r
A
, where r
A
is the radius of the
excircle of the triangle ABC opposite to A. Putting r
B
and r
C
in a similar manner, we have
P E = 2R −r
B
and P F = 2R − r
C
. Now we have
AP
2
+ P D
2
= AE
2
+ P E
2
+ P D
2
= (s − c)
2
+ (2R − r
B
)
2
+ (2R − r
A
)
2
.
Since
(2R − r
A
)
2
= 4R
2
− 4Rr
A
+ r
2
A
= 4R
2
− 4 ·
abc
4 area(4ABC)
·
area(4ABC)
s − a
+
µ
area(4ABC)
s − a
¶
2
= 4R
2
+
s(s − b)(s − c) − abc
s − a
= 4R
2
+ bc − s
2
and we can obtain (2R −r
B
)
2
= 4R
2
+ ca − s
2
in a similar way, it follows that
AP
2
+ P D
2
= (s − c)
2
+ (4R
2
+ ca − s
2
) + (4R
2
+ bc − s
2
) = 8R
2
− s
2
.
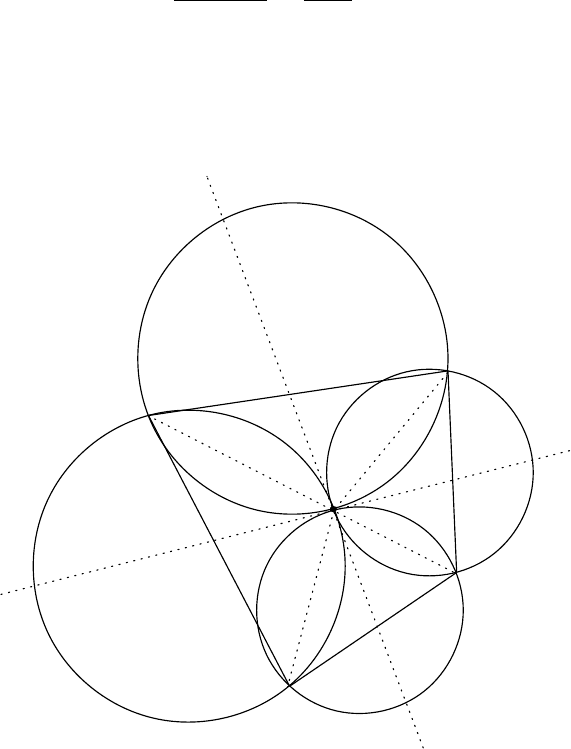
36
G4. Let Γ
1
, Γ
2
, Γ
3
, Γ
4
be distinct circles such that Γ
1
, Γ
3
are externally tangent at P , and
Γ
2
, Γ
4
are externally tangent at the same point P . Suppose that Γ
1
and Γ
2
; Γ
2
and Γ
3
; Γ
3
and Γ
4
; Γ
4
and Γ
1
meet at A, B, C, D, respectively, and that all these points are different
from P .
Prove that
AB · BC
AD ·DC
=
P B
2
P D
2
.
Solution 1.
Figure 1
Γ
1
Γ
4
Γ
3
Γ
2
P
B
A
D
C
θ
8
θ
7
θ
5
θ
6
θ
3
θ
4
θ
2
θ
1
Let Q be the intersection of the line AB and the common tangent of Γ
1
and Γ
3
. Then
∠AP B = ∠AP Q + ∠BP Q = ∠P DA + ∠P CB.
Define θ
1
, . . . , θ
8
as in Figure 1. Then
θ
2
+ θ
3
+ ∠AP B = θ
2
+ θ
3
+ θ
5
+ θ
8
= 180
◦
. (1)
Similarly, ∠BP C = ∠P AB + ∠P DC and
θ
4
+ θ
5
+ θ
2
+ θ
7
= 180
◦
. (2)
Multiply the side-lengths of the triangles P AB, P BC, P CD, P AD by P C ·P D, P D·P A,
P A · P B, P B · P C, respectively, to get the new quadrilateral A
0
B
0
C
0
D
0
as in Figure 2.
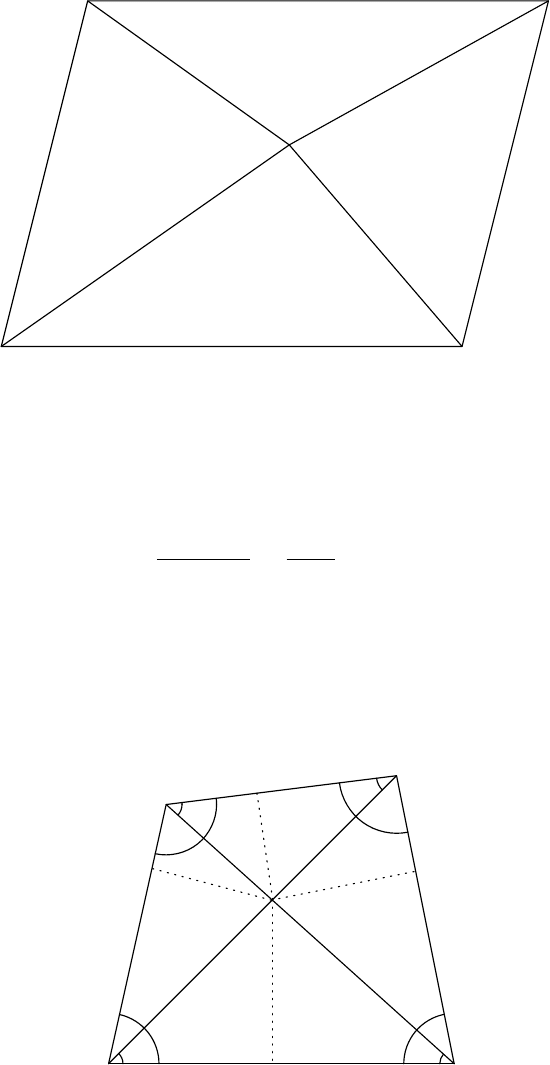
37
Figure 2
P D ·P A · P B
P B · P C ·P D
CD · P A · P B
D
0
C
0
B
0
A
0
P C ·P D · P A
AB ·P C · P D
DA · P B ·P C
P A · P B · P C
BC · P D · P A
θ
8
θ
7
θ
6
θ
5
θ
1
θ
3
θ
2
θ
4
P
0
(1) and (2) show that A
0
D
0
k B
0
C
0
and A
0
B
0
k C
0
D
0
. Thus the quadrilateral A
0
B
0
C
0
D
0
is a parallelogram. It follows that A
0
B
0
= C
0
D
0
and A
0
D
0
= C
0
B
0
, that is, AB · P C · P D =
CD ·P A · PB and AD · P B · P C = BC · P A · P D, from which we see that
AB · BC
AD ·DC
=
P B
2
P D
2
.
Solution 2. Let O
1
, O
2
, O
3
, O
4
be the centres of Γ
1
, Γ
2
, Γ
3
, Γ
4
, respectively, and let A
0
,
B
0
, C
0
, D
0
be the midpoints of PA, PB, P C, P D, respectively. Since Γ
1
, Γ
3
are externally
tangent at P , it follows that O
1
, O
3
, P are collinear. Similarly we see that O
2
, O
4
, P are
collinear.
O
1
O
2
O
3
O
4
A
0
B
0
C
0
D
0
φ
1
θ
1
φ
2
θ
2
φ
3
θ
3
φ
4
θ
4
P
Put θ
1
= ∠O
4
O
1
O
2
, θ
2
= ∠O
1
O
2
O
3
, θ
3
= ∠O
2
O
3
O
4
, θ
4
= ∠O
3
O
4
O
1
and φ
1
= ∠P O
1
O
4
,
φ
2
= ∠P O
2
O
3
, φ
3
= ∠P O
3
O
2
, φ
4
= ∠P O
4
O
1
. By the law of sines, we have
O
1
O
2
: O
1
O
3
= sin φ
3
: sin θ
2
, O
3
O
4
: O
2
O
4
= sin φ
2
: sin θ
3
,
O
3
O
4
: O
1
O
3
= sin φ
1
: sin θ
4
, O
1
O
2
: O
2
O
4
= sin φ
4
: sin θ
1
.
Since the segment PA is the common chord of Γ
1
and Γ
2
, the segment P A
0
is the altitude
from P to O
1
O
2
. Similarly PB
0
, P C
0
, P D
0
are the altitudes from P to O
2
O
3
, O
3
O
4
, O
4
O
1
,
respectively. Then O
1
, A
0
, P , D
0
are concyclic. So again by the law of sines, we have
D
0
A
0
: P D
0
= sin θ
1
: sin φ
1
.
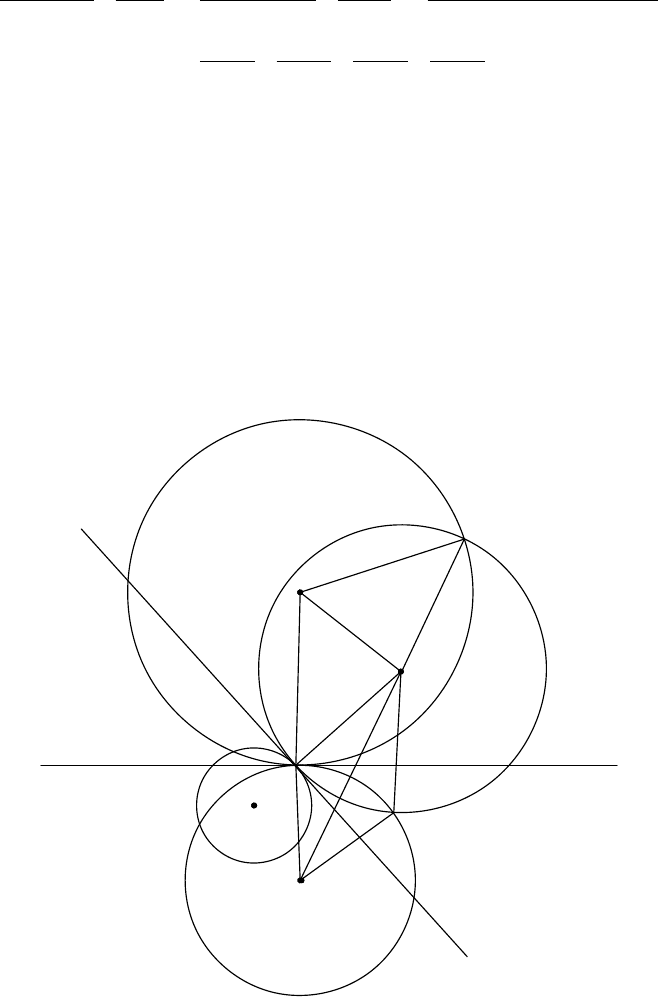
38
Likewise we have
A
0
B
0
: P B
0
= sin θ
2
: sin φ
2
, B
0
C
0
: P B
0
= sin θ
3
: sin φ
3
, C
0
D
0
: P D
0
= sin θ
4
: sin φ
4
.
Since A
0
B
0
= AB/2, B
0
C
0
= BC/2, C
0
D
0
= CD/2, D
0
A
0
= DA/2, P B
0
= P B/2, P D
0
=
P D/2, we have
AB · BC
AD ·DC
·
P D
2
P B
2
=
A
0
B
0
· B
0
C
0
A
0
D
0
· D
0
C
0
·
P D
0
2
P B
0
2
=
sin θ
2
sin θ
3
sin φ
4
sin φ
1
sin φ
2
sin φ
3
sin θ
4
sin θ
1
=
O
1
O
3
O
1
O
2
·
O
2
O
4
O
3
O
4
·
O
1
O
2
O
2
O
4
·
O
3
O
4
O
1
O
3
= 1
and the conclusion follows.
Comment. It is not necessary to assume that Γ
1
, Γ
3
and Γ
2
, Γ
4
are externally tangent.
We may change the first sentence in the problem to the following:
Let Γ
1
, Γ
2
, Γ
3
, Γ
4
be distinct circles such that Γ
1
, Γ
3
are tangent at P , and Γ
2
, Γ
4
are tangent at the same point P .
The following two solutions are valid for the changed version.
Solution 3.
Γ
1
Γ
2
Γ
3
Γ
4
O
1
O
2
O
3
O
4
A
B
C
D
P
Let O
i
and r
i
be the centre and the signed radius of Γ
i
, i = 1, 2, 3, 4. We may assume
that r
1
> 0. If O
1
, O
3
are in the same side of the common tangent, then we have r
3
> 0;
otherwise we have r
3
< 0.
Put θ = ∠O
1
P O
2
. We have ∠O
i
P O
i+1
= θ or 180
◦
− θ, which shows that
sin ∠O
i
P O
i+1
= sin θ. (1)

39
Since P B ⊥ O
2
O
3
and 4P O
2
O
3
≡ 4BO
2
O
3
, we have
1
2
·
1
2
· O
2
O
3
· P B = area(4P O
2
O
3
) =
1
2
· P O
2
· P O
3
· sin θ =
1
2
|r
2
||r
3
|sin θ.
It follows that
P B =
2|r
2
||r
3
|sin θ
O
2
O
3
. (2)
Because the triangle O
2
AB is isosceles, we have
AB = 2|r
2
|sin
∠AO
2
B
2
. (3)
Since ∠O
1
O
2
P = ∠O
1
O
2
A and ∠O
3
O
2
P = ∠O
3
O
2
B, we have
sin(∠AO
2
B/2) = sin ∠O
1
O
2
O
3
.
Therefore, keeping in mind that
1
2
· O
1
O
2
· O
2
O
3
· sin ∠O
1
O
2
O
3
= area(4O
1
O
2
O
3
) =
1
2
· O
1
O
3
· P O
2
· sin θ
=
1
2
|r
1
− r
3
||r
2
|sin θ,
we have
AB = 2|r
2
|
|r
1
− r
3
||r
2
|sin θ
O
1
O
2
· O
2
O
3
by (3).
Likewise, by (1), (2), (4), we can obtain the lengths of P D, BC, CD, DA and compute
as follows:
AB · BC
CD ·DA
=
2|r
1
− r
3
|r
2
2
sin θ
O
1
O
2
· O
2
O
3
·
2|r
2
− r
4
|r
2
3
sin θ
O
2
O
3
· O
3
O
4
·
O
3
O
4
· O
4
O
1
2|r
1
− r
3
|r
2
4
sin θ
·
O
4
O
1
· O
1
O
2
2|r
2
− r
4
|r
2
1
sin θ
=
µ
2|r
2
||r
3
|sin θ
O
2
O
3
¶
2
µ
O
4
O
1
2|r
4
||r
1
|sin θ
¶
2
=
P B
2
P D
2
.
Solution 4. Let l
1
be the common tangent of the circles Γ
1
and Γ
3
and let l
2
be that of Γ
2
and Γ
4
. Set the coordinate system as in the following figure.
40
C
Γ
4
x
y
D
Γ
3
Γ
2
B
A
Γ
1
θ
θ
We may assume that
Γ
1
: x
2
+ y
2
+ 2ax sin θ − 2ay cos θ = 0, Γ
2
: x
2
+ y
2
+ 2bx sin θ + 2by cos θ = 0,
Γ
3
: x
2
+ y
2
− 2cx sin θ + 2cy cos θ = 0, Γ
4
: x
2
+ y
2
− 2dx sin θ − 2dy cos θ = 0.
Simple computation shows that
A
µ
−
4ab(a + b) sin θ cos
2
θ
a
2
+ b
2
+ 2ab cos 2θ
, −
4ab(a − b) sin
2
θ cos θ
a
2
+ b
2
+ 2ab cos 2θ
¶
,
B
µ
4bc(b − c) sin θ cos
2
θ
b
2
+ c
2
− 2bc cos 2θ
, −
4bc(b + c) sin
2
θ cos θ
b
2
+ c
2
− 2bc cos 2θ
¶
,
C
µ
4cd(c + d) sin θ cos
2
θ
c
2
+ d
2
+ 2cd cos 2θ
,
4cd(c − d) sin
2
θ cos θ
c
2
+ d
2
+ 2cd cos 2θ
¶
,
D
µ
−
4da(d − a) sin θ cos
2
θ
d
2
+ a
2
− 2da cos 2θ
,
4da(d + a) sin
2
θ cos θ
d
2
+ a
2
− 2da cos 2θ
¶
.

41
Slightly long computation shows that
AB =
4b
2
|a + c|sin θ cos θ
p
(a
2
+ b
2
+ 2ab cos 2θ)(b
2
+ c
2
− 2bc cos 2θ)
,
BC =
4c
2
|b + d|sin θ cos θ
p
(b
2
+ c
2
− 2bc cos 2θ)(c
2
+ d
2
+ 2cd cos 2θ)
,
CD =
4d
2
|c + a|sin θ cos θ
p
(c
2
+ d
2
+ 2cd cos 2θ)(d
2
+ a
2
− 2da cos 2θ)
,
DA =
4a
2
|d + b|sin θ cos θ
p
(d
2
+ a
2
− 2da cos 2θ)(a
2
+ b
2
+ 2ab cos 2θ)
,
which implies
AB · BC
AD ·DC
=
b
2
c
2
(d
2
+ a
2
− 2da cos 2θ)
d
2
a
2
(b
2
+ c
2
− 2bc cos 2θ)
.
On the other hand, we have
MB =
4|b||c|sin θ cos θ
√
b
2
+ c
2
− 2bc cos 2θ
and MD =
4|d||a|sin θ cos θ
√
d
2
+ a
2
− 2da cos 2θ
,
which implies
MB
2
MD
2
=
b
2
c
2
(d
2
+ a
2
− 2da cos 2θ)
d
2
a
2
(b
2
+ c
2
− 2bc cos 2θ)
.
Hence we obtain
AB · BC
AD ·DC
=
MB
2
MD
2
.
42
G5. Let ABC be an isosceles triangle with AC = BC, whose incentre is I. Let P be
a point on the circumcircle of the triangle AIB lying inside the triangle ABC. The lines
through P parallel to CA and CB meet AB at D and E, respectively. The line through P
parallel to AB meets CA and CB at F and G, respectively. Prove that the lines DF and
EG intersect on the circumcircle of the triangle ABC.
Solution 1.
C
G
B
Q
D
I
A
F
E
P
The corresponding sides of the triangles P DE and CF G are parallel. Therefore, if DF
and EG are not parallel, then they are homothetic, and so DF , EG, CP are concurrent at
the centre of the homothety. This observation leads to the following claim:
Claim. Suppose that CP meets again the circumcircle of the triangle ABC at Q. Then
Q is the intersection of DF and EG.
Proof. Since ∠AQP = ∠ABC = ∠BAC = ∠P F C, it follows that the quadrilateral
AQP F is cyclic, and so ∠F QP = ∠P AF . Since ∠IBA = ∠CBA/2 = ∠CAB/2 = ∠IAC,
the circumcircle of the triangle AIB is tangent to CA at A, which implies that ∠P AF =
∠DBP . Since ∠QBD = ∠QCA = ∠QP D, it follows that the quadrilateral DQBP is
cyclic, and so ∠DBP = ∠DQP . Thus ∠F QP = ∠P AF = ∠DBP = ∠DQP , which
implies that F , D, Q are collinear. Analogously we obtain that G, E, Q are collinear.
Hence the lines DF , EG, CP meet the circumcircle of the triangle ABC at the same
point.
