Юрков Н.К. Интеллектуальные компьютерные обучающие системы

Подождите немного. Документ загружается.

231

В частном случае, когда вспомогательные атомы не включе-

ны в цепочку выполнения i-го примитива, частота f

= 0. В другом

крайнем случае f

T

, т.е. весь цикл измерений тратится на вы-

полнение вспомогательных действий.

Определим оптимальные частоты выполнения вспомогатель-

ных атомов исходя из максимума информативности процесса под-

готовки входных данных процесса проектирования.

Задача определения оптимальных частот f

имеет решение на

границе допустимого множества значений, определяемого накла-

дываемыми ограничениями. Информационные потери f

являются

монотонно убывающими функциями частот f

(чем короче интер-

вал между моментами выполнения вспомогательных действий, тем

меньше потери). Пусть вектор частот находится в некотором по-

ложении внутри разрешенной области и имеет значения своих со-

ставляющих f

, f

, …, f

. Движение от этой точки к границе облас-

ти соответствует увеличению значений всех компонент этого век-

тора, т.е. уменьшению функционала информационных потерь, что

и доказывает утверждение о наличии решения на границе. Нахож-

дение решения сводится к задаче минимизации функционала ин-

формационных потерь и имеет единственное решение.

В практических приложениях можно вводить наравне с рас-

смотренным информационным показателем качества алгоритма

проектирования и другие показатели качества и оптимизировать

затраты времени на проведение процесса подготовки и проектиро-

вания, а также материальные затраты и т.п.

Развит системно-кибернетический подход к проблеме управ-

ления сложными системами. На основе концептуальной модели

и ее взаимодействия с информационной моделью обеспечивает-

ся возможность автоматизации управления ИКОС. Доказана акту-

альность использования экспертных систем для создания «быст-

рых» моделей в тех случаях, когда настоящая модель еще не раз-

работана.

Определена основная цель работы, которая заключается в

решении крупной научной проблемы, имеющей важное народно-

хозяйственное значение, – методы и средства обработки информа-

ции, системного анализа и управления ИКОС связи, позволившей

повысить эффективность управления ИКОС в условиях неопреде-

ленности на основе современных ИТ.

232

Для разработки этой проблемы поставлены и решены задачи

теоретического, экспериментального и промышленного характера:

– разработка единого системно-кибернетического подхода к

ретроспективному и перспективному анализу и синтезу систем

управления ИКОС;

– разработка методов представления и обработки данных и

знаний, а также методов и средств постановки, проведения и пред-

ставления результатов ситуационного моделирования ИКОС;

– разработка структуры системы управления, ее логической

организации, создание методов и средств решения проблемы вы-

работки управляющих решений;

– разработка новой методики логического управления про-

изводственными процессами систем связи на основе функцио-

нально-целевого подхода;

– параметризация концептуальной модели ИКОС и ее основ-

ных компонентов, выбор структур данных, стандартов их пред-

ставления в модели и алгоритмов их обработки в ходе моделиро-

вания;

– реализация стратегии интеграции производственных и

постпроизводственных фаз жизненного цикла системы обучения;

– интеграция моделей всех этапов жизненного цикла про-

мышленного изделия на базе концептуальной модели предметной

области (КМПО) и системы межмодельного взаимодействия;

– разработка итерационного алгоритма синтеза проектного

решения, позволяющего согласовывать модели, разработанные в

разное время, разными людьми, на основе различных методов и

подходов;

– разработка методики организации информационного обме-

на между различными моделями;

– доведение теоретических предпосылок до конкретных ре-

комендаций по управлению;

– разработка алгебраического подхода к преобразованию

моделей этапов жизненного цикла системы обучения.

Определены проблемы организации управления ИКОС:

– наличие нескольких понятийных аппаратов;

– множественность центров принятия решения;

– открытость системы понятий.

Сделан вывод о наличии структурного и функционального

сходства обобщенной модели управления с механизмом эволюции

233

живой природы и процессами познания. Это доказывает, что при

всем многообразии явлений и процессов материального мира фор-

мы их организации в своей основе едины.

Дается определение сущности управления, эволюции управ-

ления, сходства процессов управления и интеллектуальной дея-

тельности (в частности, познания), а также сходства обобщенной

модели управления с механизмом эволюции живой природы. До-

казано, что повышение эффективности сознательных решений

требует создания специальной теории и соответствующих техни-

ческих средств усиления интеллектуальных возможностей челове-

ка в различных сферах его деятельности.

Показано, что современная система управления является

многоуровневой, сложной системой, включающей несколько

звеньев обратной связи, обеспечивающих регулирующие функции.

В этой системе осуществляется многоэтапное преобразование и

обобщение информации. Обработка информации в современной

системе управления невозможна без применения компьютерной

техники и современных информационных технологий. Эффектив-

ность управления существенно повышается при наличии системы

поддержки принятия решений (СППР).

Показана актуальность проблемы автоматизированного син-

теза алгоритмов управления ИКОС на основе концептуального

моделирования предметной области, которое позволяет опреде-

лить системы понятий и отношений между понятиями.

Обоснована необходимость применения функционально-

целевого подхода к анализу сложных систем. Даются основные

определения моделирования сложных систем, подробный анализ

целеобусловленности системы. Определяются требования к целям.

Разработана схема управления процессами на основе собы-

тийных моделей оборудования, потоков и процессов и имитацион-

ной модели оператора. Принципиальным отличием предложенной

схемы управления от традиционного программно-логического

управления является формирование команд управления на основе

вычисления отклонения текущего состояния технологической сети

от состояния, требуемого процессом. Это позволило вычисление

отклонения, формирование команд управления и контроль их ис-

полнения сформулировать в виде стандартных процедур, незави-

симых от конкретного приложения.

Определены особенности адаптивных систем управления.

Проведен анализ робастности системы управления.

234

Проведен анализ информационных характеристик ИКОС и

использования этих характеристик при структурно-алгоритмиче-

ском синтезе систем. Рассмотрены описательные возможности

элементарных многоэкстремальных функций и их свойства.

Таким образом, разработаны методы выработки управляю-

щих воздействий ИКОС на всех этапах жизненного цикла системы

обучения на базе ИТ, разработка которых позволила значительно

упорядочить процесс управления сложными производственными

комплексами и добиться существенного снижения непроизводст-

венных расходов, сроков разработок и производства за счет струк-

туризации существующей информации о процессе разработки и

производства систем автоматизированного обучения и обеспече-

ния эффективного управления этими процессами, а также инфор-

мационными потоками, организующими эту работу.

5.4. Интеллектуализация управления

слабо формализованными процессами

Развитие теории управления происходит в направлении ис-

следования разных сфер человеческой деятельности – от устройств

автоматики до систем управления общественными, социальными,

экономическими и другими сложными динамическими объекта-

ми [1]. Неизменным остается набор исследуемых характеристик.

Это – объект, устройство, цель и критерии качества управления.

Значительный прогресс в области математических методов,

появление новых математических моделей, широкое внедрение

компьютерных технологий позволили существенно расширить

классы исследуемых систем управления. Одним из революцион-

ных этапов можно назвать вовлечение в теорию управления моде-

лей и методов искусственного интеллекта (ИИ) и инженерии зна-

ний [48, 49].

Исследование свойств естественного интеллекта обусловило

формулировку принципов организации интеллектуальных компь-

ютерных обучающих систем [50]:

1) наличие взаимодействия управляющих систем с реальным

внешним миром с использованием информационных каналов связи;

2) открытость систем с целью повышения интеллектуально-

сти и совершенствования собственного поведения;

3) наличие механизмов прогноза изменений внешнего мира и

собственного поведения системы в динамически меняющемся

внешнем мире;

235

4) наличие у управляющей системы многоуровневой иерар-

хической структуры, построенной в соответствии с правилом: по-

вышение интеллектуальности и снижение требований к точности

моделей по мере повышения ранга иерархии в системе;

5) сохраняемость функционирования (возможно, с некоторой

потерей качества или эффективности) при разрыве связей или по-

тере управляющих воздействий от высших уровней иерархии

управляющей структуры.

Развитие методов интеллектуального управления СФП осно-

вано на привлечении различного рода моделей, отражающих ре-

альные процессы с требуемой в исследованиях точностью. Оче-

видно, что данные модели должны быть приспособлены к естест-

венному языку для лица, принимающего решения (ЛПР), а также

иметь возможность моделировать субъективные методы преобра-

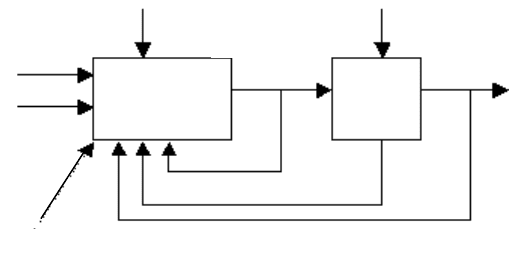
зования информации в СФП. На рис. 53 представлена обобщенная

модель систем управления СФП.

Рис. 53. Обобщенная модель системы управления СФП

Здесь X – внутреннее состояние объекта управления; Y – вы-

ходные параметры; W

, W

– возмущающие воздействия системы

управления и объекта; G – целевые воздействия; U – управляющие

воздействия; J – показатели качества; T – возможный учет време-

ни; ИСУ – интеллектуальная система управления.

Управление СФП предполагает решение двух взаимосвязан-

ных задач – задачи анализа СФП с целью построения его модели и

задачи синтеза системы управления (СУ). Поскольку СФП являет-

ся динамическим процессом, то модели СФП и СУ должны отра-

жать динамическое поведение. Ввиду того, что классы исследуе-

мых в ИКОС задач управления относятся, как правило, к дискрет-

ным процессам, определим задачи анализа СФП и синтеза СУ в

дискретном представлении.

СФП

ИСУ

236

Преимущества использования нечетких множеств в модели-

ровании СФП заключаются в их простоте и общности [51, 52].

С помощью нечеткого представления довольно несложно описать

переходы в пространстве состояний, исходя из желаемых свойств

функционирования системы. Следует подчеркнуть существенную

разницу между классическими методами приближенного анализа

сложных систем и подходом, основанным на использовании более

абстрактных моделей, к которым можно отнести и модели, осно-

ванные на нечетком представлении. В первом случае для упроще-

ния используется та же самая математическая структура, что и

сложной модели, а упрощение достигается за счет отбрасывания

той части модели, которая признается наименее важной. При вто-

ром подходе происходит переход к использованию других матема-

тических структур, которые более абстрактны, но тем не менее по-

зволяют рассматривать систему в целом, но на менее детализиро-

ванном уровне. Упрощение в последнем случае достигается за счет

отказа от несущественных деталей, а не за счет желания умень-

шить количество исследуемых переменных.

Нечеткие модели являются мостом между двумя подхода-

ми – количественным и качественным моделированием – и наибо-

лее приемлемыми для описания СФП.

С помощью нечетких логических систем имеется возмож-

ность имитации мыслительных способностей человека при описа-

нии управления процессами c использованием сравнительно не-

большого количества правил.

В настоящее время наибольший прогресс в проектировании

ИКОС достигнут для систем со свойством «интеллектуальности в

малом». Это означает, что управляющие системы, структурно не

организованные в соответствии с приведенными выше принципа-

ми ИКОС, используют при своем функционировании знания (на-

пример, в виде правил) как средство преодоления неопределенно-

сти входной информации, модели управляемого объекта или его

поведения. Известные направления в данном классе ИКОС – не-

четкие регуляторы и нейронные сети.

Выбор нечетких дифференциальных или разностных уравне-

ний очевиден ввиду их наибольшего соответствия ИКОС «в ма-

лом». При этом использование нечетких моделей обеспечивает от-

носительно простой способ управления сложными системами, ко-

торые обладают существенным нелинейным поведением. Обычно

нечеткие правила, из которых состоит нечеткий контроллер, пред-

237

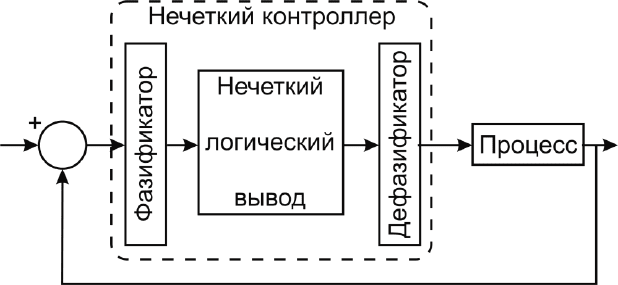
ставляют собой знания или опыт педагога. На рис. 54 представлена

общая схема нечеткого регулятора.

Рис. 54. Нечеткий регулятор как замкнутая система управления

Нечеткие регуляторы с фиксированной базой знаний извест-

ны как статические нечеткие регуляторы. Они были разработаны в

1970-е гг. как результат внедрения фундаментальных работ Л. Заде

в задачи автоматического управления [53]. Первые публикации и

значительные результаты были получены в исследовательских

группах, возглавляемых Mamdani E. H., начиная с 1970-х. База

знаний контроллера (управляющих правил) формируется путем

извлечения знаний педагога, следившего ранее за ходом протека-

ния процесса. Процедура управления представляла собой процеду-

ру моделирования, а окончательное решение принимает педагог.

Следующим шагом в направлении нечетких регуляторов как

адаптивных контроллеров является создание самоорганизующихся

нечетких логических контроллеров. Впервые они были предложе-

ны в работе [54].

Вопросы самоорганизации и самообучения в системах

управления с нечеткой логикой исследованы также в работах [55,

56]. Подобные системы широко использовались в управлении про-

цессами, в которых построение модели было затруднено либо

ожидались большие изменения значений параметров в процессе

функционирования системы. Данные алгоритмы были успешно

применены в построении автопилота морского судна, учитываю-

щего большой разброс в скорости движения судна и волнении мо-

ря. Для синтеза комбинированного управления использовалось не-

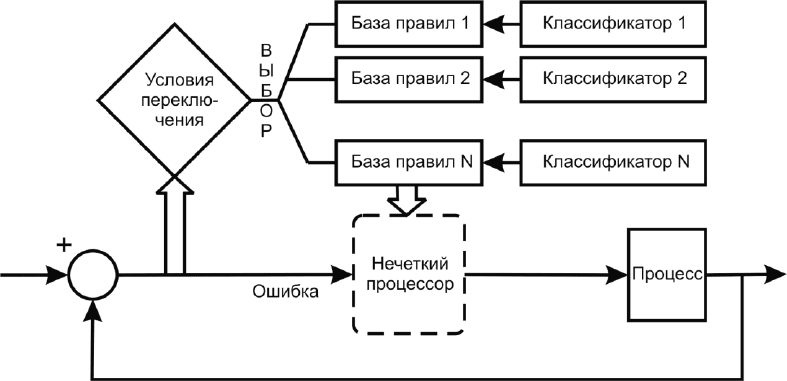
сколько параллельно включенных нечетких контроллеров. На рис.

55 представлена реализация самоорганизующегося регулятора с

квантификаторами, основное назначение которых – настройка ба-

зы правил для различных ситуаций, определяемых в блоке условий

238

переключения. База правил для разных ситуаций может содержать

не только различные правила, определяющие особенности управ-

ления на различных режимах, но и различные значения характери-

стик нечетких множеств лингвистических переменных.

Рис. 55. Самоорганизующийся комбинированный регулятор

с квантификаторами

Сами ситуации (условия переключения) определяются экс-

пертом и могут включать не только отклонения выходной коорди-

наты от требуемого значения, но и учитывать различные ограни-

чения, касающиеся общего характера функционирования динами-

ческой системы.

Например, когда выходная координата «далека» от целевого

значения, применяется один набор правил, другой набор правил

применяется при более точном управлении и т.д. до достижения

требуемой точности. Пусть для грубого управления некоторым

процессом начальный диапазон ошибки имеет разрешение

= {–1000…+1000}, универсум U

квантифицирован на восемь

уровней (лингвистических переменных), точка перехода на тонкое

управление – интервал U

= {–100…+100}, и в этом универсуме U

количество лингвистических переменных равно, например,

5 (пять уровней квантификации). Более того, для каждого уровня

управления определены свои таблицы правил. Принятие решений о

включении квантификатором той или иной модели управления осу-

ществляется на основании метазнаний, полученных от эксперта.

Наиболее полной представляется самообучаемая схема

управления, включающая эвристическую базу знаний в виде набо-

239

ра таблиц правил нечеткого регулятора, где каждая из таблиц оп-

ределяется своими правилами включения как в контур управления,

так и фактическую базу данных, основное назначение которой –

выявление новых закономерностей в практическом управлении

процессом [57]. Кроме того, с помощью базы данных осуществля-

ется обучение базы знаний, а также определяются границы интер-

валов значений лингвистических переменных в квантификаторах.

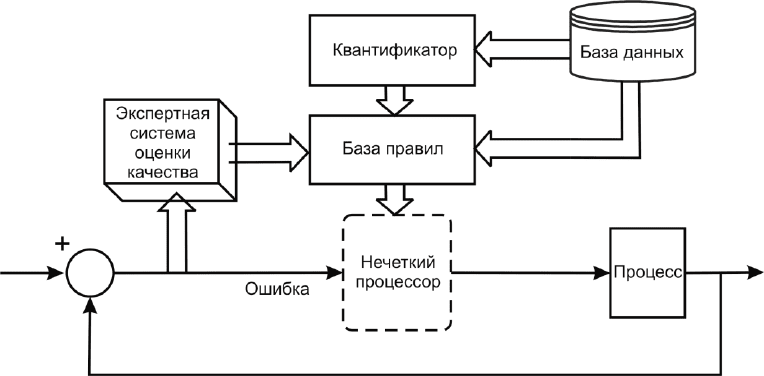
Структура такой системы представлена на рис. 56.

Рис. 56. Самоорганизующийся нечеткий регулятор с самообучением

Данная схема представляет собой наиболее полное соответ-

ствие моделирования управленческой деятельности человеком-

оператором и включает в себя следующие элементы:

1) экспертная система оценки качества управления процес-

сом, с помощью которой производится интегральная оценка каче-

ства на основе как текущего управления, так и предыдущих сеан-

сов управления, имеющихся в базе данных;

2) подсистема изменения параметров нечетких множеств и

правил базы знаний для каждого квантификационного уровня

управления;

3) подсистема поиска знаний в базе данных – KDD (Know-

ledge Discovery in Databases). Основная задача данной подсисте-

мы – проверка соответствия текущих знаний базы правил с содер-

жимым базы данных и изменение содержимого базы правил в слу-

чае нарушения такого соответствия.

Основной проблемой синтеза управления в рассмотренных

выше системах являются способы формирования базы правил,

240

обеспечивающих оптимальное регулирование сложными процес-

сами. Как правило, известные методы синтеза не рассматривают

сам процесс при решении данной задачи. Поэтому актуальным

представляется создание моделей, описывающих процессы в

ИКОС (как правило, слабо формализованные), таким образом,

чтобы задача синтеза могла быть решена некими формальными ал-

горитмами.

Из известных с 70-х гг. ХХ столетия моделей знаний – логи-

ческих, продукционных, фреймовых, нейронных и семантических

сетей – для описания слабо формализованных процессов наиболее

подходят продукционные модели знаний, с помощью которых

представляется возможным естественно описать декларативный

опыт человека, его интуицию и логику поведения [58].

Поскольку основной моделью представления системы управ-

ления в нечетких контроллерах является продукционная модель

знаний, определим в качестве базовой математической модели

описания слабо формализованных процессов (СФП) также лин-

гвистическую продукционную модель (ЛПМ). Особенностью дан-

ной модели является то, что она должна отражать динамические

связи между переменными СФП. Как и при описании контроллера,

лингвистическое описание СФП задается в виде набора правил

вида

IF X

= (x

= nb, x

= pm, …, x

= ze),

AND U

= (u

= pm, u

= nb, …, u

= nm), (5.48)

THEN X

k+1

= (x

= pb, x

= ps, …, x

= pb), (5.49)

отражающих отношения изменения состояния системы в зависи-

мости от входных воздействий. Кратко такой набор обычно запи-

сывают в виде

k+1

= X

, (5.50)

где X

= (x

, x

, …, x

) – обобщенный вектор состояния системы, а

= (u

, u

…, u

) – обобщенный вектор управляющих воздейст-

вий, значения которых представляют собой лингвистические пе-

ременные из заданного терм-множества S = {NB, NM, …, ZE, …,

PM, PB}, где NB – negative big, NM – negative middle, ZE – zero,

PM – positive middle, PB – positive big представляют собой нечет-

кие множества с заданными функциями принадлежности.

Как правило, динамическое поведение таких систем описы-

вается в виде таблиц лингвистических правил, связывающих уп-

равляющие воздействия U и выходы (либо состояния) объекта X: