Ярмолович С.В. Начертательная геометрия и инженерная графика
Подождите немного. Документ загружается.

161
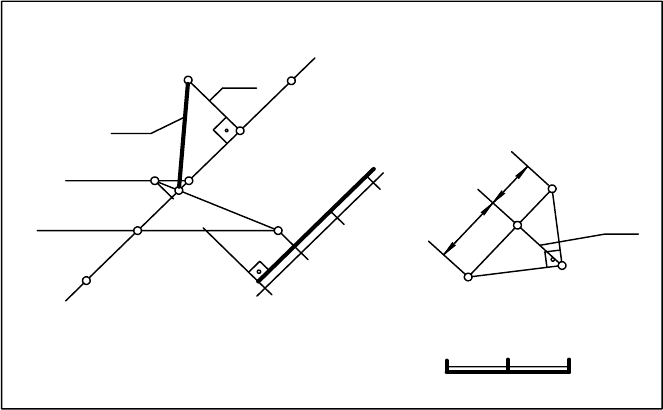
Рис. 13.19
Построения необходимо выполнять в следующей последовательно-
сти:
1. Из точки А опускаем перпендикуляр на плоскость ∆, т.е. проводим
через точку А
8
прямую, параллельную масштабу уклона ∆
i
.
2. Градуируем проекцию перпендикуляра. Для этого определим ин-
тервал перпендикуляра по формуле L
АВ
= 1/L
∆
, где L
∆
– интервал плоско-
сти, L
АВ
– интервал прямой АВ, перпендикулярной плоскости.
Интервал перпендикуляра можно определить другим способом с по-
мощью прямоугольного треугольника. Для этого в любом месте чертежа
возьмем произвольную точку В и через нее проведем отрезок ВD, равный
единице линейного масштаба. Отложим отрезок DС, равный интервалу ли-
нии наклона плоскости на перпендикуляре к прямой ВD,
соединим точки В
и С. Проведем прямую АВ, перпендикулярную ВС и пересекающуюся с
прямой DС в точке А. Отрезок АD равен интервалу перпендикуляра. От-
кладываем от точки А
8
вверх и вниз на прямой отрезки, равные интерва-
лу перпендикуляра, таким образом, чтобы отметки прямой возрастали в
сторону, противоположную направлению возрастания отметок масштаба
уклона.
3. Проведем через перпендикуляр вспомогательную плоскость, изо-
бразив ее горизонталями n
9
и n
10
.
4. Строим линию M
9
N
10
пересечения двух плоскостей (одноименные
горизонтали двух плоскостей будут пересекаться).
5. Находим точку встречи B
9,2
перпендикуляра с плоскостью. Отре-
зок А
8
B
9,2
является проекцией некоторого расстояния, натуральная величи-
на которого определена с помощью прямоугольного треугольника
А
0
А
8
К
9,2
.
L
A
B
L
∆
1
2 м
0
C
D
A
B
9
1 0
1 1
1 2
∆
i
1 м
A
8
1 0
1 1
A
0
h
1 0
h
9
B
9 . 2
н . в .
∆
h
9
7
М
9
N
1 0

162
ЛЕКЦИЯ 14. ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ
(продолжение)
14.1. Проекции тел и поверхностей.
14.2. Пересечение поверхности плоскостью.
14.3. Пересечение прямой линии с поверхностью.
14.4. Примеры решения инженерных задач в проекциях
с числовыми отметками.
14.1. Проекции тел и поверхностей
Проекции с числовыми отметками позволяют судить о форме тел по
одной горизонтальной проекции и высотным
отметкам, указывающим ха-
рактерные точки поверхности.
Многогранники задаются проекциями своих ребер с указанием отме-
ток их вершин (рис. 14.1, а и б).
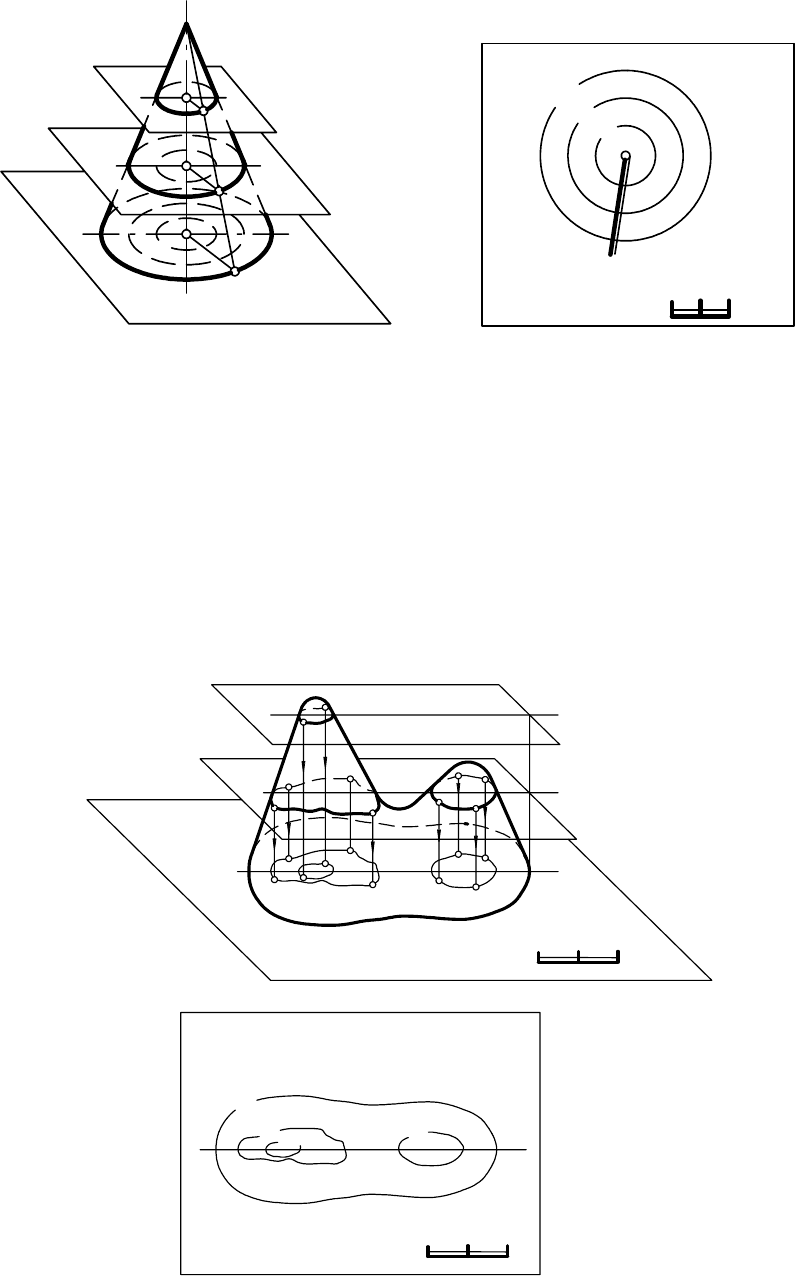
Если тела ограничены кривыми поверхностями, то они задаются
проекциями горизонтальных сечений, которые являются линиями пересе-
чения поверхности данного тела плоскостями, параллельными плоскости
П
0
и отстоящими друг от друга на расстоянии, которое называется высотой
сечения и может быть равно 1 м, 5 м, 10 м и т.д.(рис. 14.2, а и б).
а) б)
Рис. 14.1
П
0
1
0
3 м
2
S
A
B
A
1
C
2
B
4
C
S
7
A
1
C
2
1
0
3 м
2
B
4
S
7
163
а) б)
Рис. 14.2
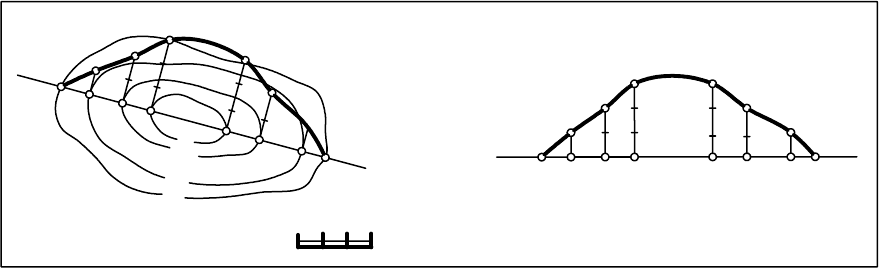
Земная (топографическая) поверхность – это поверхность случайно-
го вида, образование которой не описывается математическими законами.
Топографическая поверхность изображается проекциями горизонта-
лей, которые представляют собой линии пересечения земной поверхности
плоскостями уровня и сопровождаются отметками, указывающими высоту
сечения (рис. 14.3, а и б).
Рис. 14.3
П
0
1
0
2 м
1
0
2
S
S
3
Г
∆
0
1
2
S
3
0
1
2
П
0
5
0
1 0 м
0
1 0
2 0
1 0
0
1 0
2 0
5
0
1 0 м
П
0
0
0
a )
б )
164
14.2. Пересечение поверхности плоскостью
Линией пересечения любой поверхности плоскостью называется ли-
ния, соединяющая точки пересечения их горизонталей с одинаковыми от-
метками.
Сечение топографической поверхности вертикальной плоскостью
называется профилем.
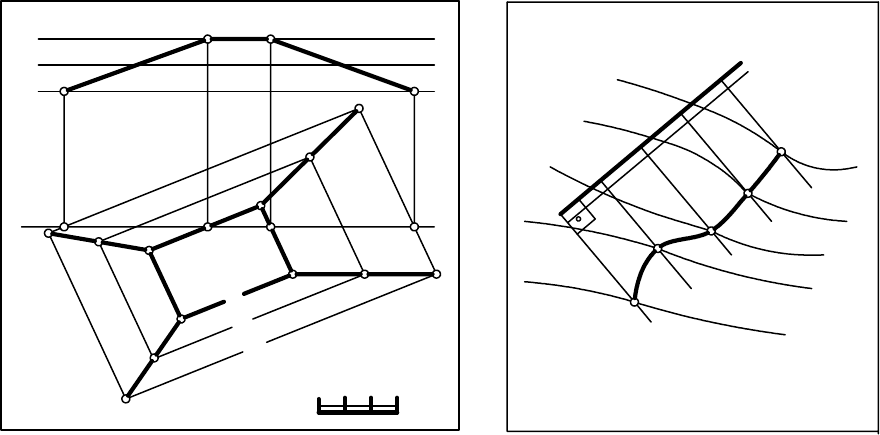
На рис. 14.4, а топографическая поверхность задана горизонталями
(17, 18, 19, 20), плоскость – горизонтальным следом, совпадающим с на-
правлением АВ. В точках пересечения прямой АВ с горизонталями
по-
верхности восстанавливаем перпендикуляры, на которых откладываем от-
метки точек и соединяем их плавной линией. Профиль можно строить со-
вмещенным с планом, можно вынести за пределы чертежа (см. рис. 14.4).
Рис. 14.4
На рис. 14.5 дано построение профиля по линии Е-Е многогранной
поверхности. Так как каждая грань поверхности является плоскостью, то
достаточно спроецировать две точки с каждой грани, чтобы получить ли-
нию пересечения этой грани плоскостью.
На рис 14.6 топографическая поверхность, заданная горизонталями
11 – 15, пересекается произвольной плоскостью, заданной масштабом
уклона ∆
i
.
Изображаем плоскость ∆ горизонталями, перпендикулярными мас-
штабу уклона ∆
i
, и находим точки пересечения одноименных горизонта-
лей. Соединяем плавной линией полученные точки. Линия L
11
M
13
N
15
явля-
ется линией пересечения поверхности плоскостью.
1 9
1 8
1 7
1 0
3 м
1 7 1 8
1 9
2 0
2 0
1 9
1 8
1 7
2
A
B
А - B
165
Рис. 14.5 Рис. 14.6
14.3. Пересечение прямой линии с поверхностью
Чтобы построить точку пересечения прямой А
8
В
12
с поверхностью,
необходимо заключить прямую в плоскость общего положения (рис. 14.7).
Для этого градуируем прямую А
8
В
12
и через точки 8, 9, 10 и 11 проводим в
произвольном направлении горизонтали, которыми задаем плоскость. Точ-
ки пересечения горизонталей с одинаковыми отметками соединяем плав-
ной кривой. Полученная линия встречается с заданной прямой в искомой
точке (К
9,8
).
Для нахождения точки пересечения прямой с поверхностью можно
использовать другой способ. На рис. 14.8 дана прямая АВ, пересекающая
топографическую поверхность. Все построения выполняем в следующем
порядке:
1) заключаем прямую в вертикальную плоскость Е-Е;
2) строим профиль топографической поверхности;
3) спроецировав прямую на вспомогательную вертикальную плос-
кость, отмечаем фронтальные проекции точек пересечения прямой
АВ с
профилем топографической поверхности.
Отметки точек определяем по их фронтальным проекциям (M
1,7
, N
2,2
).
1
0
3 м 2
5
6
7
7
6
5
1 1
1 2
1 3
1 4
1 5
1 1
1 2
1 3
1 4
1 5
∆
i
N
1 5
L
1 1
M
1 3
Е - Е
Е
Е

166
Рис. 14.7 Рис. 14.8
14.4. Примеры решения инженерных задач в проекциях
с числовыми отметками
При проектировании различных инженерных земляных сооружений,
таких как строительные площадки, железные и автомобильные дороги и
пр., приходится строить их откосы и линии пересечения этих откосов.
Откосами называются плоскости и поверхности, которые ограничи-
вают строительную площадку со всех сторон и соединяют ее
с поверхно-
стью местности.
В том случае, когда уровень строительной площадки выше уровня
поверхности местности, площадка выполняется в виде насыпи, а когда ни-
же, то в виде выемки. Углы наклона (уклона) откосов задаются при проек-
тировании сооружения и зависят от типа грунта.
Пример 1.
Построить откосы строительной площадки и определить линии
их
пересечения.
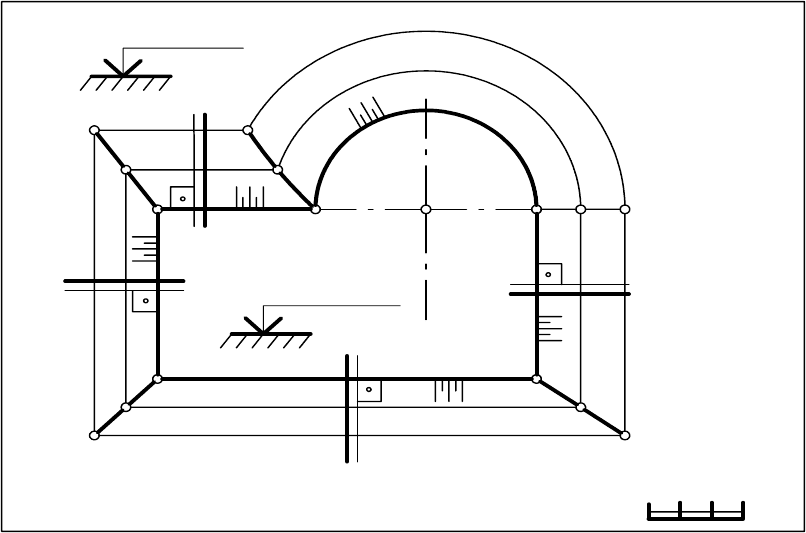
На рис. 14.9 показан план строительной площадки, ограниченной кон-
туром АВСDЕ. Отметка уровня площадки +10 м. Отметка горизонтальной
плоскости местности, на которой выполняется площадка, равна +7 м.
Площадка ограничена отрезками прямых (АВ, BC, СД, ЕА) и дугой
окружности (DЕ), центр которой находится в точке S.
Проектирование откосов площадки заключается в проведении
плоскостей
с заданным уклоном i
∆
= 1:1,5, i
Г
= 1:1,5, i
P
= 1:1, i
Т
= 1:1 че-
рез горизонтальные отрезки прямых и поверхность прямого кругового
конуса, заданного горизонталью (дуга DЕ с отметкой +10 м) и уклоном
образующей i = 1:1,5.
A
8
8
9
1 0
1 1
1 2
9
1 0
1 1
B
1 2
K
9 , 8
0
1
2
3
М
1 . 7
N
2 . 4
1
0
2
3 м
A
1 . 5
A
B
B
2 . 5
E
E
167
Рис. 14.9
Интервалы плоскостей Р и Т равны L = 1/i = 1/1:1 = 1, поэтому про-
водим горизонтали параллельно отрезкам В
10
С
10
и А
10
В
10
на расстоянии,
равном одной единице масштаба. Интервалы плоскостей Г, ∆ и конической
поверхности равны L = 1/1:1,5 = 1,5, поэтому горизонтали плоскостей Г, ∆
и горизонтали конуса, представляющие собой окружности с центром S,
проводим с интервалом, равным полутора единицам масштаба. Для опре-
деления линии пересечения откосов находим точки пересечения горизон-
талей с одинаковыми отметками. Плоскости Р
и Т, ∆ и Р, Т и Г пересека-
ются по прямым В
10
L
7
, C
10
M
7
и А
10
К
7
соответственно. Отрезок прямой
А
10
Е
10
касается дуги окружности DЕ, поэтому плоскость Г, проведенная
через этот отрезок, касается поверхности конуса, так как плоскость и кони-
ческая поверхность имеют одинаковые уклоны (Е
10
О
7
– линия касания
плоскости Г конуса).
Плоскость ∆, в отличие от плоскости Г, не касается конуса, а пересе-
кает его поверхность по кривой линии (D
10
N
7
), т.к. плоскость ∆ проводит-
ся через прямую СD, пересекающую конус. Для определения линии пере-
сечения конической поверхности плоскостью находим точки пересечения
их горизонталей с одинаковыми отметками.
M
7
∆
i
N
7
C
1 0
P
i
B
1 0
L
7
K
7
A
1 0
Τ
i
Г
i
E
1 0
O
7
S
D
1 0
8
9
9
8
9
8
9
8
1
0
2
3 м
+ 1 0 , 0 0 0
+ 7 , 0 0 0
168
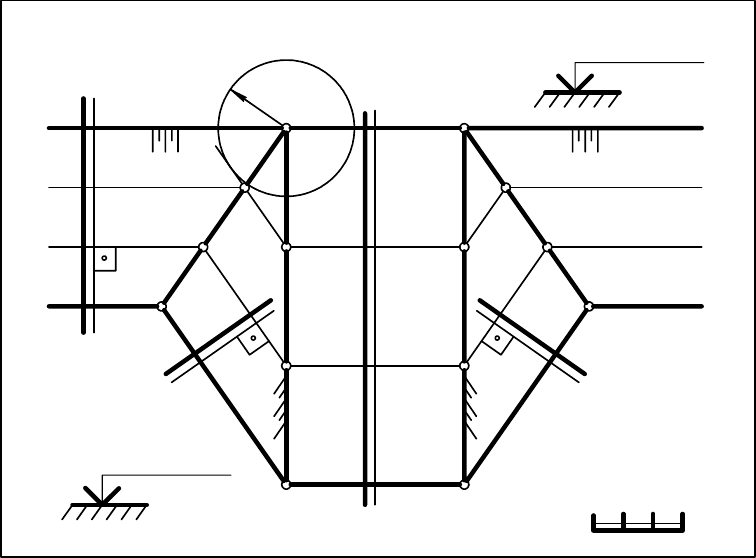
Пример 2.
Построить линии пересечения откосов горизонтальной площадки с
отметкой кромки +20 м и дороги, соединяющей площадку с местностью
(рис. 14.10).
Уклоны откосов площадки равны 1:2, уклон дороги – 1:4. Отметка
горизонтальной местности равна +17 м. Площадка выполняется в виде
насыпи.
Из рис. 14.10 видно, что дорога, соединяющая площадку с местно-
стью, является участком прямолинейной наклонной дороги.
Рис. 14.10
Кромки дороги А
20
D
17
и Е
20
F
17
не являются горизонталями, поэтому
горизонтали откоса на этом участке не параллельны им.
Решение задачи сводится к проведению плоскости заданного уклона
i = 1:2 через наклонную прямую А
20
D
17.
За вершину прямого кругового ко-
нуса с вертикальной осью примем точку А. Основание конуса расположено
в горизонтальной плоскости с отметкой 17.
Радиус основания (интервал) этого конуса определяется по формуле:
R = L = 1/i = 1/1:2 = 2 м.
Поэтому проекция горизонтали 19, проходящей через точку В
19
, кос-
нется дуги окружности, радиус которой равен двум единицам масштаба.
∆
i
P
i
Г
i
1
0
2
3 м
1 7
1 8
1 9
2 0
K
1 7
A
2 0
E
2 0
B
1 9
C
1 8
L
1 7
D
1 7
F
1 7
R
2
1 7
1 8
1 9
2 0
1
7
1
8
1
7
1
8
+ 2 0 , 0 0 0
+ 1 7 , 0 0 0
169
Остальные горизонтали этого откоса (плоскости Г) проводим через
точки прямой АD (С18, D17) параллельно горизонтали с отметкой 19. Ана-
логично строим откос (плоскость Р) через прямую Е
20
F
17
.
Горизонтали откоса (плоскости ∆) проводим с интервалом L = 1/1:2 = 2 м.
Линию пересечения откоса площадки (плоскости ∆) с откосами до-
роги (плоскостями Г и Р) определяем по точкам пересечения их горизонта-
лей с одинаковыми отметками (А
20
К
17
и Е
20
L
17
).
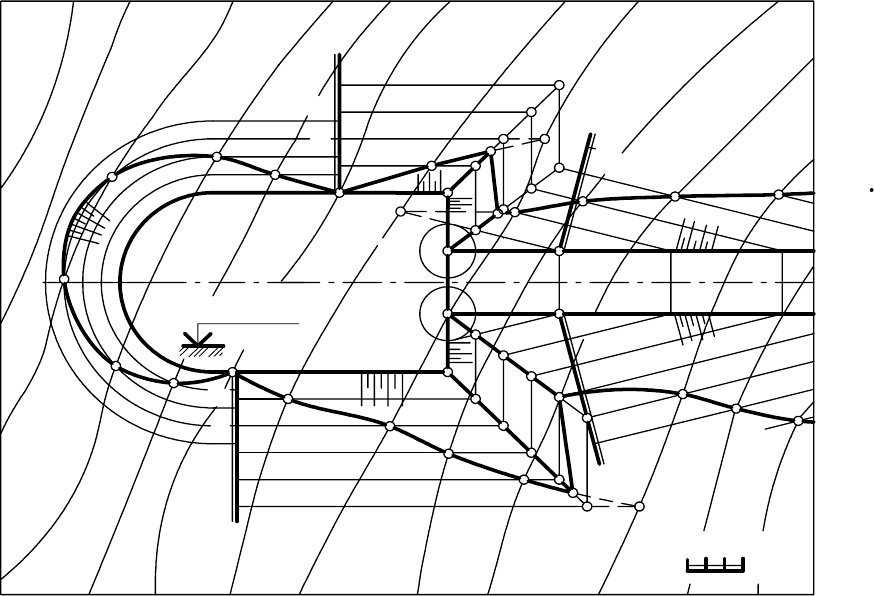
Пример 3.
Построить границы земляных работ при проектировании строитель-
ной площадки с примыкающим к ней со стороны насыпи прямолинейным
участком дороги на топографической поверхности.
На рис. 14.11 дана строительная площадка с отметкой + 42 м на за-
данной топографической поверхности. Уклоны откосов площадки равны:
уклон выемки i = 1:1, уклон насыпи 1:1,5, а уклон дороги i = 1:6.
Рис. 14.11
+ 4 2 , 0 0 0
4
1
4
0
3
9
4
0
3
8
P
i
4
0
3
8
4
4
4 6
4
0
3
8
∆
i
Г
i
3
6
4 0
3 8
4 4
4 6
4 2 4 3 4 4
4 5
4 6
4 7
4 1
4 0
3 9
3 8
3 7
3 6
3 5
Т
i
1
0
2
3 м
170
Для определения границы земляных работ необходимо выполнить
следующие построения:
1. Определить границы выемки и насыпи на пересечении 42-ой гори-
зонтали топографической поверхности с кромками площадки, имеющими
отметку 42. Точки пересечения называются точками нулевых работ.
2. Провести горизонтали откосов выемки и насыпи с интервалами
L
в
= 1/i
в
= 1 м и L
н
= 1/i
н
= 1,5 м (плоскости откосов выемки и насыпи за-
дать масштабами уклонов ∆
i
, Р
i
).
3. Провести градуирование бровок дороги (42 – 39).
Для проведения горизонталей откосов, проходящих через бровки до-
роги, необходимо провести вспомогательные конусы с радиусами основа-
ний R = L
н
= 1/i
н
= 1,5 м, т.к. дорога расположена со стороны насыпи
(плоскости откосов насыпи задать масштабами уклонов Г
i
,Т
i
).
4. Построить линии пересечения соседних откосов как точки пересе-
чения горизонталей откосов с одинаковыми отметками.
5. Построить границы земляных работ как линии пересечения отко-
сов выемки и насыпи с топографической поверхностью. Эти линии прохо-
дят через точки пересечения горизонталей откосов и горизонталей топо-
графической поверхности с одинаковыми отметками.
