Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

8.2 Ferrohydrodynamic Equations

where

is the Brownian relaxation of time at a constant. With the aid of

the torque balance equation obtained in Eq. (8.2.25), Eq. (8.2.30) can be

rearranged to yield

 

HMMMMM

uuu

IKW

(8.2.31)

The equation derived in Eq. (8.2.31) is the Shliomis magnetic relaxation

equation.

It proves useful to derive an expression of a linear form of Eq. (8.2.31)

and this is done by letting the last quadratic term of the equation to become



NmL

HMH

HMM

 uu

]

 

6 H

HNmL

HMH uu



]

(8.2.32)

by letting



MM  be respectively split into parallel and perpendicular

parts to the applied field

H , as









HMMHHMMH

uu







(8.2.33)

Combining Eqs. (8.3.32) and (8.3.33) with Eq. (8.3.30), we have a lin-

earlized magnetization equation to obtain

^`

 

HmLN

HHdt

HMH

HMHHMMH





u

]







HMHHMMH





u

ᇮ

(8.2.34)

where two characteristic relaxation times

ᇮ

and

for respectively paral-

leled and perpendicular contributions are defined where

ᇮ

(8.2.35)

and

515







]]

]

mHLN

๸

so that

is written as



]



(8.2.36)

Consequently, for a stationary limit, Eq. (8.3.34) gives a solution in the

linear order



MMM u|

(8.2.37)

Finally, in electromagnetic fields, magnetic fluids are treated as non-

conductive mediums in continuum, and to which Maxwell equations are

written as

0 u

(8.2.38)

and for the magnetic induction

0ේ  B

(8.2.39)

Equations (8.2.38) and (8.2.39) were already used to reduce ferrohydrody-

namic equations. Note that the induction

B in a continuum has a differ-

ence from the magnetic field (intensity)

H by the magnetization .M This

relation is given in Eq. (8.2.7).

Based on the thought of the intrinsic rotation of magnetic particles, a

phenomenological explanation for the increase of apparent viscosity under

plications for controlling the viscosity of a continuum by external means

are enormous, such as in damping and activating systems in engineering.

Exercise

Exercise 8.2.1 Rosensweig Equation

By considering the linear momentum equation given in Eq. (8.2.17) of

magnetic fluids, show a new set of ferrohydrodynamic equations, assum-

ing that the fluids are incompressible and at a quasi-stationary when the re-

laxation rate is so fast that

and H are sensibly collinear, i.e.

H // M

8 Magnetic Fluid and Flow

applying magnetic field is possible, which is found in Exercise 8.2.2. Ap-

516

Exercise

Also assume that all heat sources and the magnetocaloric effect are identi-

cally neglected in the energy equation.

Ans.

The continuity equation of an incompressible medium is written as

0 

(1)

under the assumption of

H // M

, that is

 gu

UKU

HMp

ේේ

(2)

The equation (2) is a so-called Rosensweig equation, first proposed by

Ronald Rosensweig (1964). The research of magnetic fluids has continued

from the original work of Rosensweig (1964).

The energy equation is reduced to the temperature field equation, and

is written repeatedly as







(3)

The magnetization is expressed by the magnetic state equation



THMM , , so that it is written by the Langevin formula as



]

NmLM for TkmH

]

(4)

where



coth

]]]

 L .

Treating the magnetic fluids to be nonconductive, the electromagnetic

field equations are then written where

ේ u H and 0ේ  B

(5)

For magnetic polarization of magnetic fluids, we have

MHB 

(6)

This set of equations, which are yielded in a closed system, can be solved

with appropriate boundary conditions.

Exercise 8.2.2 Rotational Viscosity

Probably one of the most noticeable features of magnetic fluids is an in-

crease of apparent viscosity under a magnetic field. Based on the idea that

517

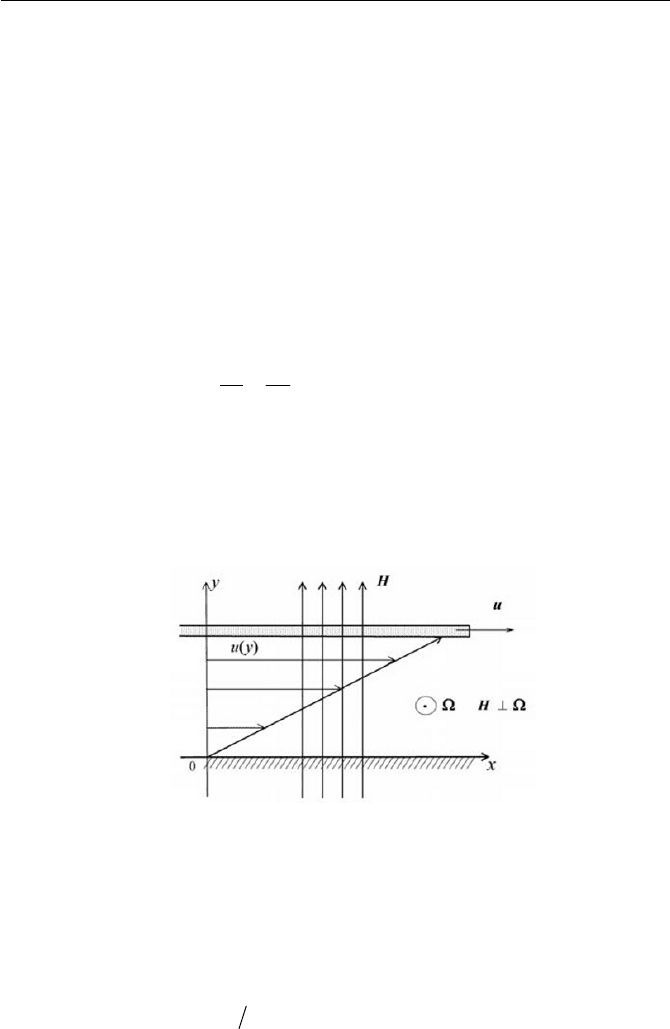
the intrinsic rotation

Ȧ of a particle deviates from the angular velocity

of the fluid particle, it will be reasonable to think that the difference

leads to an additional dissipation, which may be understood to contribute

an increase of apparent viscosity. An example of the simple flow field is

displayed in Fig. 8.5.

Verify the increase of the apparent viscosity under the condition where

the applied magnetic field

H is perpendicular to .

Ans.

In considering Eq. (8.2.33), the perpendicular part of



MM  to the

applied field

H is written as

^`

๸

uu



HMM

(1)

The steady state solution of Eq. (8.2.34) is given where, i.e. from the resul-

tant Eq. (8.2.37),



0๸0

MMM u 

(2)

Fig. 8.5 One example of

H A

in a Couette flow

Using these conditions, i.e. H //

M and H A , a combination of Eqs. (1)

and (2) yields



HM u

(3)

By noting that



2uu and substituting Eq. (3) to the linear momen-

tum equation given in Eq. (8.2.17), we have

8 Magnetic Fluid and Flow

518

Problems



gHMHMu

UKU

uu

gHMu

UWK





HMp

(4)

As the results obtained from the form of Eq. (4), the second term of the

right hand side of the equation indicates that there appears an additional

viscous term

where

r 0

(5)

The increase of the apparent viscosity in

is regarded as the rotational

viscosity, Shliomis (1972). Eq. (5) can be expressed in combination with

the Langevin formula given in Eq. (8.1.1) and the definition

given in

Eq. (8.2.36) as follows



]]

IK]K

tanh







vvr

(6)

In the absence of a magnetic field, i.e. 0

]

, Eq. (6) leads



in which an individual particle rotates with the same angular velocity as a

fluid particle, followed by

. On the other hand, in the limiting case

for fo

]

, we have



IKK

(7)

Problems

8.2-1 Prove that

is expressed in the formula given in Eq. (8.2.36).

Ans.

useful. are 8.1.1 Exercise

8.2-2 Sketch the curve given in Eq. (6) in Exercise 8.2.2, and discuss the

increase of the apparent viscosity where



]

. Keep other parame-

ters constants.

519

8.2-3 Assuming 0

Ȧ , Eq. (8.2.25) gives HM

6 u . Substitu-

tion of this

HM u to Eq. (8.2.17), gathering the viscous terms,

yields





23 

. Derive this expression and discuss the

consequence of Exercise 8.2.2, i.e.





23  f .

Ans.

particles of slipping the

implies while

particles, of rolling

theimplies0

]

8.3 Basic Flows and Applications

Among many interesting phenomena that often characterize magnetic flu-

ids, some typical cases are explained in this text. In order to avoid confu-

sion and complexity, phenomenological explanations are chiefly given

here, trying not to go into too much detailed mathematical treatments. One

very characteristic response is the normal field instability. The spontane-

ous generation of an ordered pattern of peaks (spikes) on the interface (the

surface exposed to atmosphere for example) occurs when a uniform mag-

netic field (exceeding a critical intensity) is applied perpendicular to the

interface of a magnetic fluid. Figure 8.6 displays the surface spikes gener-

ated due to a normal instability. Among other interesting phenomena con-

nected with the instability problem in a magnetic fluid is that an instability

produces a labyrinthine or maze pattern that occurs in a thin layer of a

magnetic fluid, when the layer is contained between a closely spaced flat

surfaces, where furthermore possible patterns can appear in different con-

mathematically as a bifurcation and are treated as a critical phenomenon,

resulting in many patterns appearing at supercritical stages of new equilib-

rium flow fields. The thermomagnetic convection followed by the appear-

ance of cell patterns is also generated due to the flow instability under

various conditions of magnetic fields. This is known as thermoconvective

instability.

In this section we shall start our discussion to derive the ferrohydrody-

namic Bernoulli equation. Many flow problems in magnetic fluid’s tech-

nology can be explained similar to, yet in a more augmented way, the

Bernoulli equation. Some problems of the thermoconvective instability are

treated, taking account of the temperature dependence of magnetization.

8 Magnetic Fluid and Flow

figurations of imposing magnetic fields. These phenomena are known

520

8.3 Basic Flows and Applications

Fig. 8.6 Surface spikes due to

the normal instability

8.3.1 Generalized Bernoulli Equation

Denoting that magnetic fluids are incompressible and at quasi-stationary

where

HM //

is satisfied, the ferrohydrodynamic equation represented by

a Rosensweig equation is written as

UKU

 HMp

ේේේ

(8.3.1)

A peculiar feature of the equation describing magnetic fluids is associ-

ated with an additional volume force

ේ , the Kelvin force density and

the composite pressure

p appearing in place of a hydrostatic pressure

In this sense, Eq. (8.3.1) is an extended Navier-Stokes equation. Denote

that

is the gravitational body force in Eq. (8.3.1).

Along with assumptions adapted for derivation of a Bernoulli equation

in Chapter 4, we assume that the fluid is inviscid

, irrotational

0ේ u u

and isothermal

Constant T

. With the condition of a steady

state

0 ww tu , Eq. (8.3.1) can be reduced to the following form



ේ

෾



HdHMup

(8.3.2)

where z

is the gravitational potential. The last term can be alterna-

tively written by using the field-averaged magnetization, which is defined

)

521



HdHM

(8.3.3)

so that



HMHdHM

(8.3.4)

The integration (along the stream line or vortex line) of Eq. (8.3.2)

yields a more convenient form where

const.

 HMzpu g

(8.3.5)

In comparing Eq. (8.3.5) with Eq. (4.1.38), Eq. (8.3.5) is called a ferrohy-

drodynamic Bernoulli equation, where a new term

 appears in the

Bernoulli equation. The importance of Eq. (8.3.5) in view of engineering

flow problems will be illustrated in proceeding sections.

8.3.2 Hydrostatics

With a limit of flow speed 0ou , the state of fluids is at a hydrodynami-

cally static state, where the pressure distribution in a stationary magnetic

fluid is described as a static equilibrium equation, derived from Eq. (8.3.5),

as follows

 



HdHMzzpp

(8.3.6)

where

p is the composite pressure at the point where



0000

zyx ,, x in

which

and the axis z is directed vertically upward.

Now let us consider a situation when a nonmagnetic body immersed in

a magnetic fluid, similar to that what considered in Fig.3.3. The force act-

ing on a body is determined by a stress

T on the surface element Sd , as

similarly treated in Eq. (3.1.9)

dSHp

HBII



(8.3.7)

8 Magnetic Fluid and Flow 522

8.3 Basic Flows and Applications

T is derived from Eq. (8.2.9), together with the Maxwell stress tensor in

Eq. (8.2.13) for the condition of hydrodynamically static state. At the

boundary (at the surface) of the body, the induction B has to satisfy the

condition

0 

dSB

(8.3.8)

Leading to Eq. (8.3.7) to write



dSp

nMF



(8.3.9)

Equation (8.3.9) indicates that at the surface of body, the pressure bound-

ary condition becomes

ConstMp



(8.3.10)

The second term of Eq. (8.3.10) is called the magnetic normal traction, in-

dicating that there would be a magnetic pressure jump at the interface of a

body and a magnetic fluid. Extensive discussion on the magnetic normal

traction is found in Berkovsky et al. (1993).

In general, the calculation of the surface integral for Eq. (8.3.9) yields

the net force

. However, in reality obtaining



HMM

is difficult

since a non-magnetic body immersed in a magnetic fluid disturbs an exter-

nal field and resultantly alters



xHH at the surface of the body. Within

the tolerance it is reasonable to assume that

HM 

, which enables us

to neglect the magnetic normal traction. The force

is thus, by using Eq.

(8.3.6), written as



dSHdHMzdSp

nnF

ˆˆ

³³³



 

(8.3.11)

where the magnetic field



xHH is assumed the same as those prior to

immersing the body .

Equation (8.3.11) can also be rewritten by the Gauss’ divergence theo-

rem as follows



³³



 

dVHM

dVpdsp

(8.3.12)

523

If we further assume that within the volume of a non-magnetic body,

HM

is kept constant as g does, we can write Eq. (8.3.12) to give

VHMV )(  g

(8.3.13)

The first term in Eq. (8.3.13) is the buoyant force known as the princi-

ple of Archimedes with reference to Eq. (3.1.30); the second term of the

equation is the magnetic buoyant force, whose direction is determined by

H of a magnetic field (where we assume HM // ).

When the choice of the direction of H



is controlled to be the same as

the gravity acceleration

g , which effectively increases the flotation effect

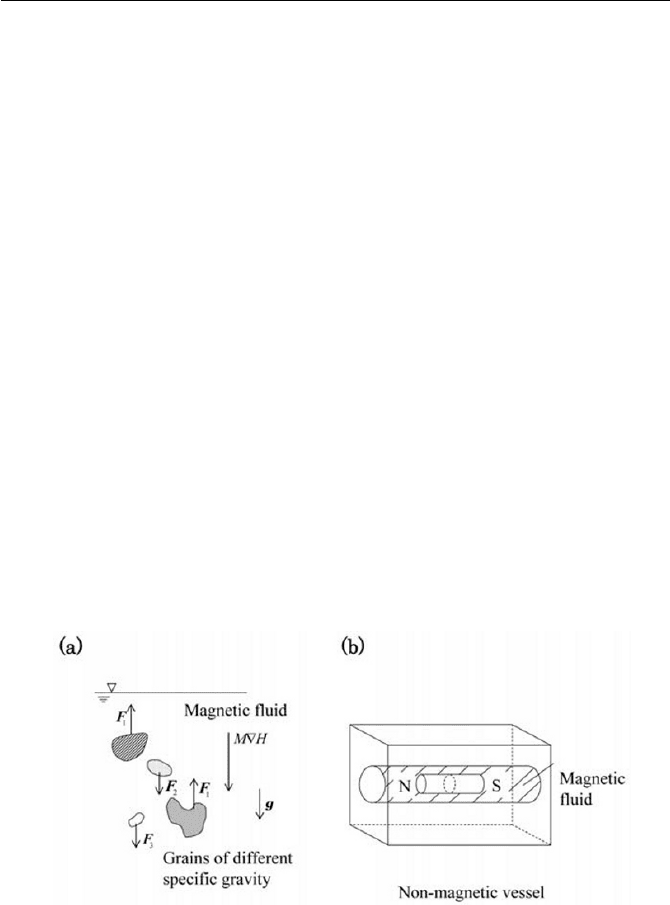
for a non-magnetic body. This effect leads to wide applications in practical

engineering. One of which is ore separation with respect to specific gravi-

ties, as schematically displayed in Fig. 8.7(a). The buoyant force of the

preset magnitude is applied to floating valuable substances, separated from

other grains of ore. On the contrary, in a case where the flotation condi-

tions of non-magnetic bodies change in the presence of an external non-

uniform field, magnetic bodies are self-levitating. For example, if a per-

manent magnet is placed in a non-magnetic vessel filled with a magnetic

fluid, the magnet floats stably alone at the bottom of the vessel, being re-

pelled from the side walls and resultantly occupying a position in the ves-

sel, as sketched in Fig. 8.7(b). The self-levitating effect is the basis for the

development of accelerometers, level meter or inertia dampers in engineer-

ing applications.

Fig. 8.7 Magnetostatic buoyancy effects

The magnetic hydrostatic equation given in Eq. (8.3.6), suggests that the

body force due to the field gradient yields a pressure gradient, as is

straightforwardly stated from the Rosensweig equation given in Eq. (8.3.1)

for the static condition of

0 u

. The presence of a pressure gradient under

8 Magnetic Fluid and Flow 524