Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.

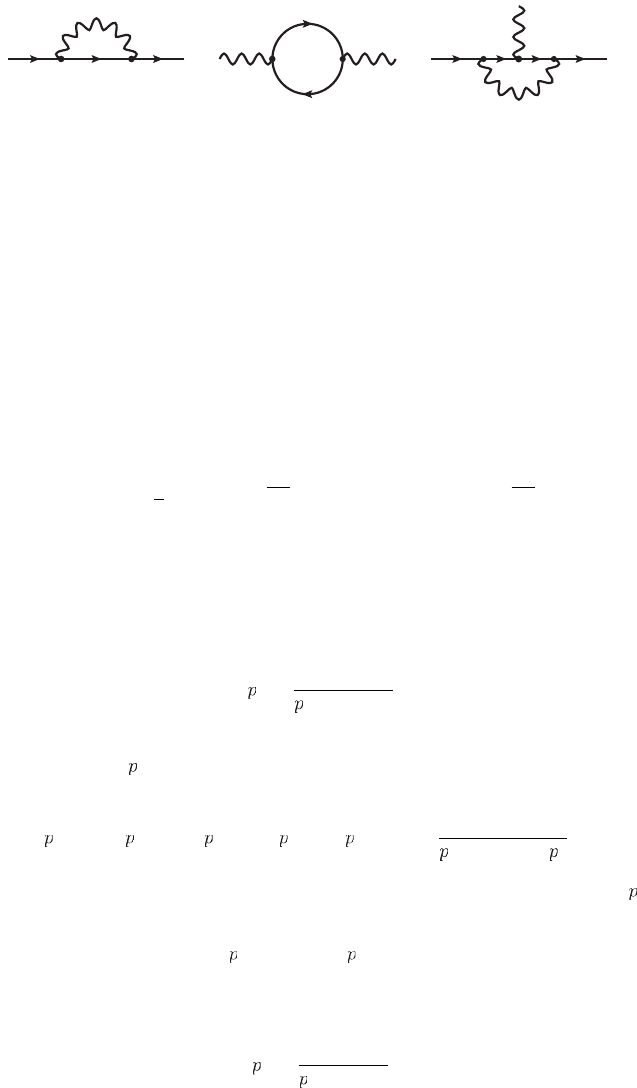
2
6
2 Neutrinos within the
S
tandard Model
(
a
)
(
b
)
(
c
)
Fig. 2.1 The one-loop Feynman diagrams for
(
a
)
the electron self-energy,
(
b
)
the
photon self-energy and
(
c
)
the electron-photon vertex in QE
D
a
nd
S
in-Itiro Tomona
g
a
f
ound a solution to this problem in
Q
ED in the
l
ate 1940’s
(
Schwinger, 1958
)
. In modern language, the mass and coupling
parameters present in t
h
ec
l
assica
l
Lagrangian are t
h
eso-ca
ll
e
db
are quanti
-
ties which will receive radiative corrections at the quantum level.
O
ne mus
t
d
ecom
p
ose the bare
q
uantities into the renormalizable ones and the countert
-
erms: the renormalizable quantities are physical and can be confronted wit
h
t
h
e experimenta
l
o
b
serva
bl
es, w
h
i
l
et
h
e counterterms are use
d
to cance
l
t
he
i
nfinities arising from the quantum corrections. Hence we should rewrite th
e
L
agrangian of QED in Eq.
(
2.4
)
in terms of bare quantities:
L
Q
ED
=
−
1
4
F
0
μν
F
F
0
μν
+
Ψ
0
i
γ
μ
∂
μ
−
i
e
0
A
0
μ
Ψ
0
−
m
0
Ψ
0
Ψ
0
,
(
2.22
)
where
F
0
μν
F
=
∂
μ
A
0
ν
−
∂
ν
A
0
μ
.
It is well known that a quantum field theor
y
is
c
haracterized by its Green functions. In order to see where the infinity comes
f
rom and how to deal with it, here we consider the simplest
G
reen
f
unctio
n
of QED
(
i.e., the electron propagator
)
at the one-loop level. The tree-leve
l
propagator of a free electron i
s
i
S
F
(
/
p
//
)=
i
/
p
//
−
m
0
+i
.
(
2.23
)
The
f
ull propa
g
ator can be
fig
ured out by evaluatin
g
the one-loop electron
s
elf-energ
y
−
i
Σ
(
/
p
//
)
, for which the Feynman diagram is given in Fig. 2.1
(
a
)
.
To
b
eexp
l
icit, we
h
av
e
i
S
F
(
/
p
/
/
)
=
i
S
F
(
/
p
/
/
)
+i
S
F
(
/
p
/
/
)
−
i
Σ
(
/
p
/
/
)
i
S
F
(
/
p
/
/
)
+
·
·
·
=
i
/
p
//
−
m
0
−
Σ
(
/
p
//
)
,
(
2.24
)
where the infinite insertions of the electron self-energy are implied, and
Σ
(
/
p
//
)
c
an be treated as a perturbative quantit
y
. Because o
f
Lorentz invariance
,
Σ
(
/
p
//
)
=
A
(
p
2
)
+
/
pB
//
(
p
2
)
(
2.25
)
h
olds. Then the ph
y
sical mass of the electron can be identified as the pole of
the
f
ull propa
g
ator
i
S
F
(
/
p
/
/
)
=
i
Z
2
/
p
/
/
−
m
+i
.
(
2.26
)
2
.1 Fundamentals o
f
the
S
tandard Model 2
7
whe
r
e
m
=
Z
2
(
m
0
+
A
)
is just the renormalized or physical mass of th
e
electron with
Z
−
1
2
≡
1
−
B
b
ein
g
the wave function renormalization con-
s
tant. One may similarly obtain the renormalized propagator of the photon:
i
D
μ
ν
(
p
2
)
=
−
i
Z
3
Z
g
μν
/
(
p
2
+
i
)
, for which the one-loop Feynman diagram i
s
s
hown in Fig. 2.1
(
b
)
. We can absorb the constants
Z
2
an
d
Z
3
Z
b
y rescalin
g
the electron and photon
fi
elds
Ψ
0
≡
Z
1
/
2
2
Ψ
a
n
d
A
0
μ
=
Z
1
/
2
3
Z
A
μ
.As
f
o
rr
ad
i
a-
tive corrections to the electron-photon vertex in Fig. 2.1
(
c
)
,onemayintro-
d
uce t
h
ep
h
ysica
l
e
l
ectric c
h
arg
e
e
b
y using anot
h
er renorma
l
ization constan
t
e
0
Z
2
Z
1
/
2
3
Z
=
eZ
1
.
The bare Lagrangian of QED can therefore be divided int
o
the renormalized terms and their counterterms
(
Peskin and Schroeder, 1995
)
L
Q
ED
=
−
1
4
F
μν
F
F
μν
+
Ψ
i
γ
μ
∂
μ
−
i
e
A
μ
Ψ
−
m
ΨΨ
−
1
4
δZ
3
Z
F
μν
F
F
μν
+
Ψ
i
γ
μ
δZ
2
∂
μ
−
i
δZ
1
eA
μ
Ψ
−
δ
mΨΨ
,
(
2.27
)
where
δZ
i
Z
≡
Z
i
Z
−
1
(
for
i
=1
,
2
,
3
)
an
d
δ
m
≡
Z
2
m
0
−
m have been defined.
Starting from this Lagrangian one can immediately read off the relevant Feyn-
m
an rules and calculate the
G
reen
f
unctions includin
g
the contributions
f
rom
the counterterms.
A
detailed calculation shows that the infinities arise fro
m
the integration over the loop momentum. Such infinities can be removed by
c
hoosin
g
suitable renormalization constant
s
δZ
i
Z
a
n
d
δm
,f
or instance, b
y
im-
posing the renormalization condition
s
Σ
(
/
p
//
)
/
p
/
/
=
m
=
0
,
d
Σ
(
/
p
//
)
d
/
p
d
/
/
/
p
//
=
m
=0
;
(
2.28
)
a
n
d
Π
(
p
2
)
p
2
=0
=
0
,
i
e
Γ
μ
(
p
,
p
)
|
p
−
p
=
0
=i
e
γ
μ
,
(
2.29
)
w
h
ere
Π
(
p
2
)
an
d
Γ
μ
(
p,
p
)
stand respectively for the photon self-energy and
t
h
epropere
l
ectron-p
h
oton vertex. It is wort
h
mentionin
g
t
h
at t
h
ere
l
ation
Z
1
=
Z
2
e
xactly holds to all orders in QED as a consequence of the
g
au
g
e
i
nvariance. T
h
is i
d
entity ensures t
h
at t
h
ep
h
ysica
l
e
l
ectric c
h
arge
e
or t
h
e
g
au
g
e couplin
g
constant is universal
f
or all the char
g
ed particles. The
f
ul
l
renormalization of
Q
ED has been described in some standard textbooks o
f
q
uantum field theories
(
Peskin and Schroeder, 1995; Weinberg, 1995
)
.
A
proof of the renormalizability of non-
A
belian
g
au
g
etheoriesismor
e
c
omplicated. First comes the quantization of non-
A
belian gauge fields. T
o
preserve the gauge invariance or to satisfy the Ward-Takahashi identity,
F
e
y
nman
f
ound that scalar particles with the Fermi-Dirac statistics wer
e
n
ecessary in the calculation of the one-loop self-energies of gauge bosons
(
Feynman, 1963
)
. In the path-integral language Ludvig Faddeev and Victor
P
opov pointed out that these stran
g
e scalar particles arose
f
rom removin
g
th
e
f
reedom of gauge invariance
(
Faddeev and Popov, 1967; De Witt, 1967
)
.It
2
8
2 Neutrinos within the
S
tandard Model
was even unc
l
ear w
h
et
h
er t
h
espontaneous
g
au
g
e symmetry
b
rea
k
in
g
wou
ld
s
poil the renormalizabilit
y
of the whole theor
y
or not in the 1960’s. In 1971,
Gerardus ’t Hooft gave the first complete proof of the renormalizability o
f
n
on-Abelian gauge theories
(
’t Hooft, 1971a, 1971b; Lee and Zinn-Justin,
1
972a, 1972b, 1972c
)
. Since then, the Weinberg-Salam model has gradually
been accepted to be the standard theory of electroweak interactions.
2.1.4 The
S
tandard Electroweak Model
O
ne o
f
the
g
reatest successes in particle physics is the establishment o
f
the
u
nified theory of electromagnetic and weak interactions, or the SM of elec
-
t
r
oweak
in
te
r
act
i
o
n
s
.T
h
i
s
m
odel
i
s based o
n
the
SU
(
2
)
L
×
U
(
1
)
Y
g
au
g
e
g
roup, and its
g
au
g
e symmetry is spontaneously broken down to
U
(
1
)
Q
.The
U
(
1
)
Q
gauge
b
oson, w
h
ic
h
is just t
h
ep
h
oton,
k
eeps mass
l
ess
d
ue to t
h
e gaug
e
i
nvariance. In contrast, t
he
SU
(
2
)
L
g
au
g
e
b
osons acquire t
h
eir masses via t
he
H
i
gg
s mechanism and mediate the short-ran
g
e weak interactions. In the S
M
the left-handed components of quarks and leptons are assigned to be th
e
SU
(
2
)
L
doublets
Q
L
≡
u
L
d
L
,
c
L
s
L
,
t
L
b
L
;
L
≡
ν
e
L
e
L
,
ν
μ
L
μ
L
,
ν
τ
L
τ
L
ττ
.
(
2.30
)
The ri
g
ht-handed components o
f
quarks and leptons are all th
e
S
U
(
2
)
L
si
n
-
glets defined a
s
U
R
U
U
≡
u
R
,
c
R
,
t
R
;
D
R
≡
d
R
,s
R
,b
R
;
E
R
≡
e
R
,μ
R
,τ
R
ττ
.
(
2.31
)
N
ote that onl
y
the le
f
t-handed components o
f
three neutrinos take part in
weak interactions, because they have been assumed to be the massless Weyl
particles in the
SM
1
.Q
uarks and leptons also carry the hyperchar
g
e
s
Y
,
which are related to the weak isos
p
i
n
I
3
components and the electric char
g
es
Q
t
h
roug
h
t
h
ere
l
ation
Q
=
I
3
+
Y
.
Table 2.1 is a list of all the quantum
n
umbers o
f
quarks and leptons in the
S
M
.
A
s discussed in Section 2.1.1, the
g
au
g
e fields should be introduced t
o
m
aintain the local gauge invariance via the definition of covariant derivatives.
He
n
ce t
h
e
kin
et
i
cte
rm
soffe
rmi
o
n
fie
l
ds a
r
e
L
F
=
Q
L
i
/
DQ
//
L
+
L
i
/
D
//
L
+
U
R
UU
i
/
∂
//
U
R
U
U
+
D
R
i
/
∂
//
D
R
+
E
R
i
/
∂
//
E
R
,
(
2.32
)
where the covariant derivatives are defined a
s
D
μ
≡
∂
μ
−
i
g
τ
k
W
k
μ
W
−
i
g
YB
μ
,
1
T
he discovery of neutrino oscillations implies that neutrinos must be massive
.
Hence the
S
M is actually incomplete. The possibilities o
f
incorporatin
g
massive
neutrinos into the SM will be discussed in Chapters 3 and 4
.

2
.1 Fundamentals o
f
the
S
tandard Model 2
9
T
able 2.1 Quantum numbers of quarks and leptons in the SM
Partic
l
econtent Wea
k
isos
p
i
n
I
3
Hyperc
h
ar
ge
Y
El
ectric c
h
ar
g
e
Q
Q
L
≡
⎛
⎝
⎛
⎛
u
L
d
L
⎞
⎠
⎞⎞
,
⎛
⎝
⎛⎛
c
L
s
L
⎞
⎠
⎞⎞
,
⎛
⎝
⎛
⎛
t
L
b
L
⎞
⎠
⎞⎞
⎛
⎝
⎛⎛
+
1/2
−
1
/
2
⎞
⎠
⎞
⎞
+1
/
6
⎛
⎝
⎛⎛
+
2
/
3
−
1
/
3
⎞
⎠
⎞⎞
L
≡
⎛
⎝
⎛
⎛
ν
e
L
e
L
⎞
⎠
⎞
⎞
,
⎛
⎝
⎛⎛
ν
μ
L
μ
L
⎞
⎠
⎞⎞
,
⎛
⎝
⎛⎛
ν
τ
L
τ
L
ττ
⎞
⎠
⎞⎞
⎛
⎝
⎛⎛
+
1
/
2
−
1
/
2
⎞
⎠
⎞
⎞
−
1
/
2
⎛
⎝
⎛⎛
0
−
1
⎞
⎠
⎞⎞
U
R
UU
≡
u
R
,
c
R
,
t
R
0
+2
/
3
+
2
/
3
D
R
≡
d
R
,s
R
,b
R
0
−
1
/
3
−
1
/
3
E
R
≡
e
R
,μ
R
,τ
R
ττ
0
−
1
−
1
∂
μ
≡
∂
μ
−
i
g
YB
μ
.
(
2.33
)
N
ote tha
t
τ
k
τ
≡
σ
k
/
2(
for
k
=
1
,
2
,
3
)
and
Y
d
enote the generators of the
g
au
g
e
g
roup
s
SU
(
2
)
L
a
n
d
U
(
1
)
Y
, respectively. In Eq.
(
2.33
)
,
g
a
n
d
g
a
r
e
the correspondin
gg
au
g
e couplin
g
constants.
S
ince the
g
au
g
e
fi
elds are als
o
d
ynamic, t
h
eir
k
inetic terms are given
b
y
L
G
=
−
1
4
W
i
μν
W
i
μν
W
−
1
4
B
μν
B
μν
(
2.34
)
wit
h
W
i
μν
W
≡
∂
μ
W
i
ν
WW
−
∂
ν
W
i
μ
W
+
gε
ijk
W
j
μ
W
W
k
ν
WW
,
B
μν
≡
∂
μ
B
ν
−
∂
ν
B
μ
,
(
2.35
)
w
h
ere
W
i
μ
W
(
for
i
=
1
,
2
,
3)
an
d
B
μ
a
re t
he
SU
(
2
)
L
an
d
U
(
1
)
Y
g
auge
b
osons,
respectively. It is straightforward to verify that Eqs.
(
2.32
)
and
(
2.34
)
are
g
au
g
e-invariant. However, the local
g
au
g
e symmetry must be broken; i.e.
,
SU
(
2
)
L
×
U
(
1
)
Y
→
U
(
1
)
Q
,
w
h
ere
U
(
1
)
Q
is just the gauge group of QED. Th
e
s
ymmetry
b
rea
k
in
g
can
b
erea
l
ize
db
ya
dd
in
g
a
d
ou
bl
et sca
l
a
r
H
≡
(
φ
+
,
φ
0
)
T
,
which has the hypercharge
Y
(
H
)
= +1. The gauge-invariant Lagrangian for
t
h
e sca
l
a
r
fie
l
ds
r
eads
L
H
=
(
D
μ
H
)
†
D
μ
H
−
μ
2
H
†
H
−
λ
H
†
H
2
,
(
2.36
)
where
μ
2
is real and
λ
i
s real and positive. To figure out the particle spectrum,
one has to determine the vacuum o
f
the theory by minimizin
g
the scala
r
p
otential. I
f
μ
2
>
0
, the minimum is located at the original point
(
i.e.
,
H
≡
0
|
H
|
0
=
0
)
. In this case the vacuum state is also invariant under the gauge
30
2 Neutrinos within the
S
tandard Model
trans
f
ormation, such that the
g
au
g
e symmetry o
f
thetheoryispreserved.I
f
μ
2
<
0
, the minima are fixed b
y
2
|
H
|
2
=
1
2
v
2
,
(
2.37
)
whe
r
e
v
=
−
μ
2
/λ
i
st
h
evevof
H
.
Eq.
(
2.37
)
shows that there exist infinite
a
nd de
g
enerate vacua. Once one chooses a special direction
,
H
=
1
√
2
0
v
,
(
2.38
)
t
h
e
g
au
g
e symmetry is
b
ro
k
en
d
own an
d
t
h
e correspon
d
in
gg
au
g
e
b
osons
g
e
t
m
asses. To make this point clear, we parametrize the Hi
gg
s doublet a
s
H
=e
i
τ
k
ξ
k
(
x
)
/v
1
√
2
0
v
+
h
(
x
)
,
(
2.39
)
whe
r
e
ξ
k
(
x
)(
for
k
=1
,
2
,
3
)
an
d
h
(
x
)
stand for the four degrees of freedo
m
i
n
t
h
e doub
l
et
H
.A
fter performin
g
the
g
au
g
e transformation wit
h
U
(
ξ
)=
e
−
i
τ
k
ξ
k
(
x
)
/
v
, we turn to the unitary gauge. In this case the transformed Higgs
a
nd
g
au
g
e
fi
elds ar
e
H
=
1
√
2
0
v
+ h
(
x
)
,
τ
k
W
k
μ
W
=
U
(
ξ
)
τ
k
W
k
μ
W
U
−
1
(
ξ
)
−
i
g
∂
μ
U
(
ξ
)
U
−
1
(
ξ
)
.
(
2.40
)
In the unitary
g
au
g
e only one physical scalar boson
h
s
urvives, and the
g
au
g
e
bosons are no longer massless. The latter can be understood from the second
equation in Eq.
(
2.40
)
: there is a longitudinal polarization o
f
W
k
μ
W
i
n
co
n
t
r
ast
w
i
th the
m
assless o
r
t
r
a
n
sve
r
se
W
k
μ
W
g
auge
b
osons.
A
fter spontaneous
g
au
g
e symmetry breakin
g
, let us proceed to discuss
the
p
article s
p
ectrum of the SM
.
(
1
)
The masses of gauge bosons come from the first term in Eq.
(
2.36
):
v
2
8
01
gσ
k
W
k
μ
W
+
g
B
μ
gσ
k
W
kμ
+
g
B
μ
0
1
=
v
2
8
W
1
μ
W
W
2
μ
W
W
3
μ
W
B
μ
⎛
⎜
⎛⎛
⎜
⎜⎜
⎝
⎜⎜
g
2
00 0
0
g
2
00
0
0
g
2
−
gg
00
−
gg
g
2
⎞
⎟
⎞⎞
⎟
⎟⎟
⎠
⎟⎟
⎛
⎜
⎛⎛
⎜
⎜⎜
⎝
⎜⎜
W
1
μ
W
2
μ
W
3
μ
B
μ
⎞
⎟
⎞⎞
⎟
⎟⎟
⎠
⎟⎟
.
(
2.41
)
A
s usual, we define the physical
g
au
g
e bosons
2
O
ne might wonder what will happen if
μ
2
= 0. In fact, it has been proved that
t
h
espontaneous
g
au
g
e symmetry
b
rea
k
in
g
can
b
etri
gg
ere
db
yra
d
iative corrections
even if
μ
2
is vanishing at the tree-level (Coleman and Weinberg, 1973).

2
.1 Fundamentals o
f
the
S
tandard Model
31
W
±
μ
W
≡
1
√
2
W
1
μ
W
∓
i
W
2
μ
W
(
2.42
)
a
nd
Z
μ
Z
A
μ
=
cos
θ
w
−
s
in
θ
w
sin
θ
w
cos
θ
w
W
3
μ
W
B
μ
.
(
2.43
)
T
h
ewea
k
mixin
g
an
gle
θ
w
and masses o
fg
au
g
e bosons can be determined
f
rom the diagonalization of the mass matrix in Eq.
(
2.41
):
ta
n
θ
w
=
g
g
,M
2
W
MM
±
=
1
2
gv , M
2
Z
M
0
=
1
2
g
2
+
g
2
v
.
(
2.44
)
Note t
h
at
A
μ
d
escribes the photon, whose mass keeps vanishin
g
because th
e
U
(
1
)
Q
gauge symmetry is unbroken. Both the charged gauge boson
s
W
±
a
nd
t
h
eneutra
lg
au
g
e
b
oso
n
Z
0
are massive, an
d
t
h
eir masses are proportiona
l
to the vev o
f
the Hi
gg
s
fi
eld. Th
e
W
±
a
n
d
Z
0
p
articles were experimentall
y
d
iscovered by Carlo Rubbia, Simon van der Meer and the UA1 Collaboration
i
n 1983 at CERN
(
Arnison
et al.
, 1983a, 1983b
)
. Their masses, together wit
h
the weak mixin
g
an
g
le θ
w
,
have now been measured to a hi
g
hde
g
ree o
f
acc
ur
ac
y
:
M
W
MM
=(
8
0
.
398
±
0
.
0
25
)
GeV,
M
Z
M
=
(
9
1
.1
876
±
0
.
0
021
)
GeV and
sin
2
θ
w
=0
.
23119
±
0
.
0
0014
(
Nakamur
a
et al
., 2010
)
.
(
2
)
The mass of the Higgs boson arises from the last two terms
(
i.e., the
H
iggs potential
)
in Eq.
(
2.36
)
. More explicitly,
V
(
H
)
≡
μ
2
H
†
H
+
λ
H
†
H
2
=
−
μ
2
h
2
+
λ
v
h
3
+
λ
4
h
4
+
1
4
μ
2
v
2
.
(
2.45
)
H
ence the mass o
f
the Hi
gg
s boson
h
is
M
h
M
=
−
2
μ
2
. It is worth stressin
g
that the Higgs boson is the only SM particle that has not been observed.
C
urrent experimental lower bound on
M
h
M
is
M
h
M
>
114
.
4
GeV at the 95
%
c
onfidence level
(
Nakamura et al
.
, 2010
)
. Recently, a combined analysis o
f
the data from the
C
DF and D
0C
ollaborations at the Fermilab Tevatron ha
s
excluded a
S
MHi
gg
s boson in the mass ran
g
e 162
G
eV
<M
h
M
<
1
66 G
e
V
a
t the 95% confidence level
(
Aaltonen et al
.
, 2010
)
. The search for the Higgs
boson is the main mission of the Large Hadron Collider
(
LHC
)
,whichis
runnin
g
with the center-o
f
-mass ener
g
y
√
s
f
rom 7 TeV to 14 TeV at
C
ERN
.
(
3
)
The masses of six quarks and three charged leptons stem from the
Y
ukawa
in
te
r
act
i
o
n
s
L
Y
=
−
Q
L
Y
u
YY
˜
HU
R
UU
−
Q
L
Y
d
Y
Y
HD
R
−
L
Y
l
YY
HE
R
+
h
.
c
.
,
(
2.46
)
where
˜
H
≡
i
σ
2
H
∗
i
s defined
,
Y
u
Y
Y
,
Y
d
YY
an
d
Y
l
Y
Y
are the
3
×
3Yukawacouplin
g
m
atrices. After the Hi
gg
s field acquires its vev, the mass matrices of up-typ
e
q
uarks, down-type quarks and char
g
ed leptons are respectively
g
iven by
M
u
MM
=
1
√
2
vY
u
YY
,M
d
MM
=
1
√
2
vY
d
YY
,M
l
M
=
1
√
2
vY
l
YY
,
(
2.47
)
3
2 2 Neutrinos within the
S
tandard Model
whe
r
e
v
2
46
G
eV.Theycansimplybedia
g
onalized by means o
f
the bi
-
u
nitar
y
transformations
U
†
u
UU
M
u
M
M
U
u
U
U
=D
ia
g
{
m
u
,
m
c
,
m
t
}
,U
†
d
U
M
d
MM
U
d
UU
=
D
ia
g
{
m
d
,m
s
,m
b
}
,
U
†
l
U
M
l
M
U
l
U
=
Dia
g
m
e
,
m
μ
,m
τ
,
(
2.48
)
w
h
ere
m
q
(
for q
=
u
,
c
,t
or
d,
s
,b
)
and
m
α
(
fo
r
α
=
e
,μ,
τ
)
stand respectivel
y
f
or the physical masses o
f
quarks and char
g
ed leptons. These nine
f
undamen
-
tal
p
arameters of the SM have all been determined with the hel
p
of
Q
ED,
QCD and relevant experimental data
(
Nakamur
a
et al.
,
2010
)
,andtheirval
-
u
es at a
g
iven ener
g
y sca
l
eex
h
i
b
it t
h
e puzz
l
in
gh
ierarc
h
ies
m
u
m
c
m
t
,
m
d
m
s
m
b
an
d
m
e
m
μ
m
τ
.
A combination of Eqs.
(
2.32
)
,
(
2.34
)
,
(
2.36
)
and
(
2.46
)
leadsustothe
f
ull La
g
ran
g
ian o
f
the
S
M at the classical level. The quantization o
f
the non-
A
belian gauge fields will involve the gauge-fixing terms and the Faddeev-
P
opov
g
host
fi
elds, as excellently described in some standard textbooks
(
Cheng and Li, 1988; Peskin and Schroeder, 1995; Weinberg, 1995
)
.Inthe
s
ubse
q
uent sections we shall focus our attention on the interactions of neu
-
trinos with quarks and leptons within the
S
M.
2
.2
S
tandard Interactions o
f
Neutrinos
In view o
f
the
f
act that neutrinos can weakl
y
interact with other elementar
y
p
articles via W
±
a
nd
Z
0
, let us first of all give a brief summary of th
e
c
harged-current and neutral-current interactions of quarks, charged lepton
s
a
nd neutrinos in the
S
M
.
(
1
)
Eq.
(
2.32
)
allows us to fix the charged-current interactions of quarks
:
L
q
cc
=
g
Q
L
γ
μ
τ
1
W
1
μ
W
+
τ
2
ττ
W
2
μ
W
Q
L
=
g
√
2
Q
L
γ
μ
τ
+
W
+
μ
W
Q
L
+h
.
c
.
=
g
√
2
uct
L
γ
μ
⎛
⎝
⎛⎛
d
s
b
⎞
⎠
⎞
⎞
L
W
+
μ
W
+
h
.
c
.,
(
2.49
)
whe
r
e
W
+
μ
W
a
n
d
W
−
μ
W
h
ave been defined in Eq.
(
2.42
)
,an
d
τ
+
≡
τ
1
+i
τ
2
ττ
=
01
00
,
τ
−
≡
τ
1
−
i
τ
2
ττ
=
00
1
0
.
(
2.50
)
A
s shown in Eq.
(
2.48
)
, one may always diagonalize the quark mass matrices
M
u
MM
a
n
d
M
d
M
b
yusin
g
the bi-unitary trans
f
ormations. This treatment is equiv-
a
lent to transforming the flavor eigenstates of up- and down-type quarks into
their mass eigenstates
(
u
,c
,
t
a
n
d
d
,s
,b
)
.Then
L
q
cc
ca
n
be
r
ew
ri
tte
n
as

2.2
S
tandard Interactions o
f
Neutrinos
33
L
q
cc
=
g
√
2
u
c
t
L
γ
μ
V
⎛
⎝
⎛⎛
d
s
b
⎞
⎠
⎞⎞
L
W
+
μ
W
+h
.
c
.
,
(
2.51
)
where
V
≡
U
†
u
UU
U
d
U
i
s the Cabibbo-Kobayashi-Maskawa
(
CKM
)
quark fla-
vor mixing matrix
(
Cabibbo, 1963; Kobayashi and Maskawa, 1973
)
. A full
p
arametrization o
f
V
n
eeds three mixin
g
an
g
les and one
C
P-violatin
g
phase
,
whose values have all been measured to a very good degree of accuracy
(
Naka
-
mu
r
a
et al
.
,
2010
)
. Similarly, the charged-current interactions of leptons are
d
escribed b
y
L
l
cc
=
g
√
2
eμτ
L
γ
μ
⎛
⎝
⎛⎛
ν
e
ν
μ
ν
τ
⎞
⎠
⎞⎞
L
W
−
μ
W
+h
.
c
..
(
2.52
)
S
ince neutrinos are massless in the
S
M, it is alwa
y
spossibletomakethemas
s
eigenstates of charged leptons and neutrinos simultaneously coincide wit
h
their corresponding flavor eigenstates. In other words, there is no lepton flavor
m
ixin
g
.I
f
three neutrinos have non-de
g
enerate masses, however, a
C
KM
-
l
ike lepton flavor mixing matrix will appear i
n
L
l
cc
. The phenomenology of
n
eutrino masses and lepton flavor mixing will be discussed in Chapter 3
.
(
2
)
Eq.
(
2.32
)
can also allow us to determine the neutral-current interac
-
tions of
q
uarks:
L
q
n
c
=
g
Q
L
γ
μ
τ
3
ττ
Q
L
W
3
μ
W
+
g
Q
L
γ
μ
Y
Q
L
+
U
R
UU
γ
μ
YU
R
U
U
+
D
R
γ
μ
Y
D
R
B
μ
=
3
i
=
1
g
q
i
q
i
L
γ
μ
I
3
q
I
i
L
0
0
I
3
q
i
L
q
i
q
i
L
W
3
μ
W
+
g
q
i
q
i
L
γ
μ
Y
q
Y
Y
i
L
0
0
Y
q
i
L
q
i
q
i
L
B
μ
+
g
q
i
q
i
R
γ
μ
Y
q
YY
i
R
0
0
Y
q
i
R
q
i
q
i
R
B
μ
,
(
2.53
)
whe
r
e
q
i
a
n
d
q
i
(
fo
r
i
=
1
,
2
,
3
)
run over
(
u
,c,t
)
and
(
d
,s,
b
)
, respectively.
The neutral-current interactions of leptons can analo
g
ously be written out.
With the help of Eq.
(
2.43
)
, we express the weak neutral-current interaction
s
o
f
quarks and leptons in terms o
f
the physical
g
au
g
e
fi
el
d
Z
μ
Z
:
L
n
c
=
g
cos
θ
w
f
C
f
L
CC
f
L
ff
γ
μ
f
L
ff
Z
μ
Z
+
C
f
R
CC
f
R
f
f
γ
μ
f
R
ff
Z
μ
Z
,
(
2.54
)
whe
r
e
C
f
L
CC
≡
I
3
f
I
L
−
Q
f
s
in
2
θ
w
,
C
f
R
CC
≡
I
3
f
I
R
−
Q
f
s
in
2
θ
w
,
an
d
f
r
u
n
sove
r
all
q
uarks and leptons. The explicit results o
f
C
f
L
CC
a
n
d
C
f
R
CC
a
r
el
i
sted
in T
able
2.2.
In addition, the electroma
g
netic interactions o
f
leptons and quarks take the
s
ame form as in
Q
ED:

3
4 2 Neutrinos within the
S
tandard Model
L
EM
=
e
f
Q
f
fγ
μ
fA
μ
,
(
2.55
)
w
i
th
Q
f
=
I
3
f
I
+
Y
f
YY
.
S
ometimes it is more convenient to expres
s
L
n
c
as a sum
of the vector- and
p
seudovector-current contributions. In this case
,
L
n
c
=
g
cos
θ
w
f
f
γ
μ
C
f
V
CC
−
C
f
A
C
γ
5
fZ
μ
Z
,
(
2.56
)
whe
r
e
C
f
V
CC
≡
C
f
L
CC
+
C
f
R
CC
,C
f
A
C
≡
C
f
L
CC
−
C
f
R
CC
.
(
2.57
)
The explicit results of
C
f
V
CC
a
n
d
C
f
A
C
a
re a
l
sogiveninTa
bl
e2.2
.
Table 2.2 The coefficient
s
C
f
L
CC
a
nd
C
f
R
versu
s
C
f
V
C
C
a
nd
C
f
A
C
f
or weak neutral-curren
t
interactions of leptons and quarks in the SM, where
f
=
u, d,
l
o
r
ν
de
n
otes t
h
e
up-type quar
k
s,
d
own-type quar
k
s, c
h
ar
g
e
dl
eptons or neutrinos, respective
ly
f
=u
f
=
d
f
=
lf
=
ν
C
f
L
CC
+
1
2
−
2
3
sin
2
θ
w
−
1
2
+
1
3
s
i
n
2
θ
w
−
1
2
+si
n
2
θ
w
+
1
2
C
f
R
C
C
−
2
3
s
i
n
2
θ
w
+
1
3
sin
2
θ
w
s
i
n
2
θ
w
0
C
f
V
C
C
+
1
2
−
4
3
s
i
n
2
θ
w
−
1
2
+
2
3
sin
2
θ
w
−
1
2
+
2s
i
n
2
θ
w
+
1
2
C
f
A
C
+
1
2
−
1
2
−
1
2
+
1
2
I
nthe
f
ollowin
g
we shall elaborate on the neutrino interactions by takin
g
af
ew t
y
pical examples — neutrino-electron, neutrino-neutrino and neutrino-
n
ucleon scattering processes
.
2.2.1 Neutrino-electron
S
catterin
g
L
et us first calculate the cross section of the elastic neutrino-electron scat-
tering process
ν
e
+
e
−
→
ν
e
+
e
−
,w
h
ic
hh
as p
l
aye
d
an important ro
l
ein
d
etectin
g
solar neutrinos. The invariant amplitude
f
or
ν
e
(
p
,
s
ν
)+
e
−
(
q
,
s
e
)
→
ν
e
(
p
,
s
ν
)
+ e
−
(
q
,
s
e
)
receives contributions from both neutral- and charged-
c
urrent interactions, as shown in Fi
g
.2.2.Wei
g
nore the trans
f
erred ener
g
y
i
n the low-ener
g
yre
g
ion since it is much smaller than
M
W
MM
a
n
d
M
Z
M
.
In
t
hi
s
good approximation the amplitude for neutral-current interactions i
s

2.2
S
tandard Interactions o
f
Neutrinos
35
ν
e
ν
e
−
ν
e
ν
Z
0
W
+
ν
e
ν
e
−
e
−
e
−
ν
e
ν
Fig. 2.2 Feynman diagrams for the elastic neutrino-electron scattering process
ν
e
+
e
−
→
ν
e
+
e
−
in the
S
M
M
n
c
(
s
ν
,s
e
;
s
ν
,s
e
)=
−
g
2
4
M
2
Z
M
cos
2
θ
w
C
ν
L
CC
u
(
p
,
s
ν
)
γ
μ
(1
−
γ
5
)
u
(
p
,
s
ν
)
×
u
(
q
,s
e
)
γ
μ
C
l
L
CC
(1
−
γ
5
)
+
C
l
R
CC
(
1+
γ
5
)
u
(
q
,s
e
)
,
(
2.58
)
a
nd the amplitude for char
g
ed-current interactions read
s
M
cc
(
s
ν
,s
e
;
s
ν
,s
e
)
=
−
g
2
8
M
2
W
MM
u
(
q
,s
e
)
γ
μ
(1
−
γ
5
)
u
(
p
,
s
ν
)
×
u
(
p
,s
ν
)
γ
μ
(1
−
γ
5
)
u
(
q
,
s
e
)
.
(
2.59
)
The overall amplitude is the sum of Eqs.
(
2.58
)
and
(
2.59
)
. Before going into
the details of our calculations, we briefly review the Fierz transformations
.
It is we
ll k
nown t
h
at an ar
b
itrary
4
×
4 matrix can
b
eexpan
d
e
d
in t
h
e
b
asi
s
of sixteen inde
p
endent matrice
s
Γ
r
(
fo
r
r
=1
,
2
,
···
,
16
)
defined as
Γ
1
≡
1
4
,
Γ
2
,
3
,
4
,
5
≡
γ
μ
,
(
fo
r
μ
=
0
,
1
,
2
,
3
)
,
Γ
6
,
7
,
8
,
9
,
1
0
,
1
1
≡
σ
μν
,
(
fo
r
μ
,
ν
=0
,
1
,
2
,
3
an
d
μ
<ν
)
,
Γ
12
,
13
,
14
,
15
≡
i
γ
μ
γ
5
,
(
fo
r
μ
=
0
,
1
,
2
,
3)
,
Γ
16
≡
γ
5
.
(
2.60
)
It is easy to verify that the normalization relatio
n
T
r
[
Γ
r
Γ
s
Γ
]
=4
δ
r
s
(
2.61
)
h
olds
(
fo
r
r
,
s
=
1
,
2
,
···
,
1
6
)
, where the subscripts imply that the correspond-
i
n
g
Lorentz indices should be lowered down by the metric tensor. Conside
r
t
h
epro
d
uc
t
P
=
16
r
=1
g
r
Ψ
1
ΨΨ
Γ
r
Ψ
2
ΨΨ
Ψ
3
ΨΨ
Γ
r
ΓΓ
Ψ
4
Ψ
=
16
r
=1
g
r
(
Γ
r
)
α
β
(
Γ
r
ΓΓ
)
ηλ
Ψ
1
Ψ
Ψ
α
(
Ψ
2
ΨΨ
)
β
Ψ
3
Ψ
Ψ
η
(
Ψ
4
Ψ
)
λ
,
(
2.62
)
