Wooldridge J. Introductory Econometrics: A Modern Approach (Basic Text - 3d ed.)
Подождите немного. Документ загружается.


could wind up with different conclusions. Reporting the significance level at which we are
carrying out the test solves this problem to some degree, but it does not completely remove
the problem.
To provide more information, we can ask the following question: What is the largest
significance level at which we could carry out the test and still fail to reject the null hypoth-
esis? This value is known as the p-value of a test (sometimes called the prob-value).
Compared with choosing a significance level ahead of time and obtaining a critical value,
computing a p-value is somewhat more difficult. But with the advent of quick and
inexpensive computing, p-values are now fairly easy to obtain.
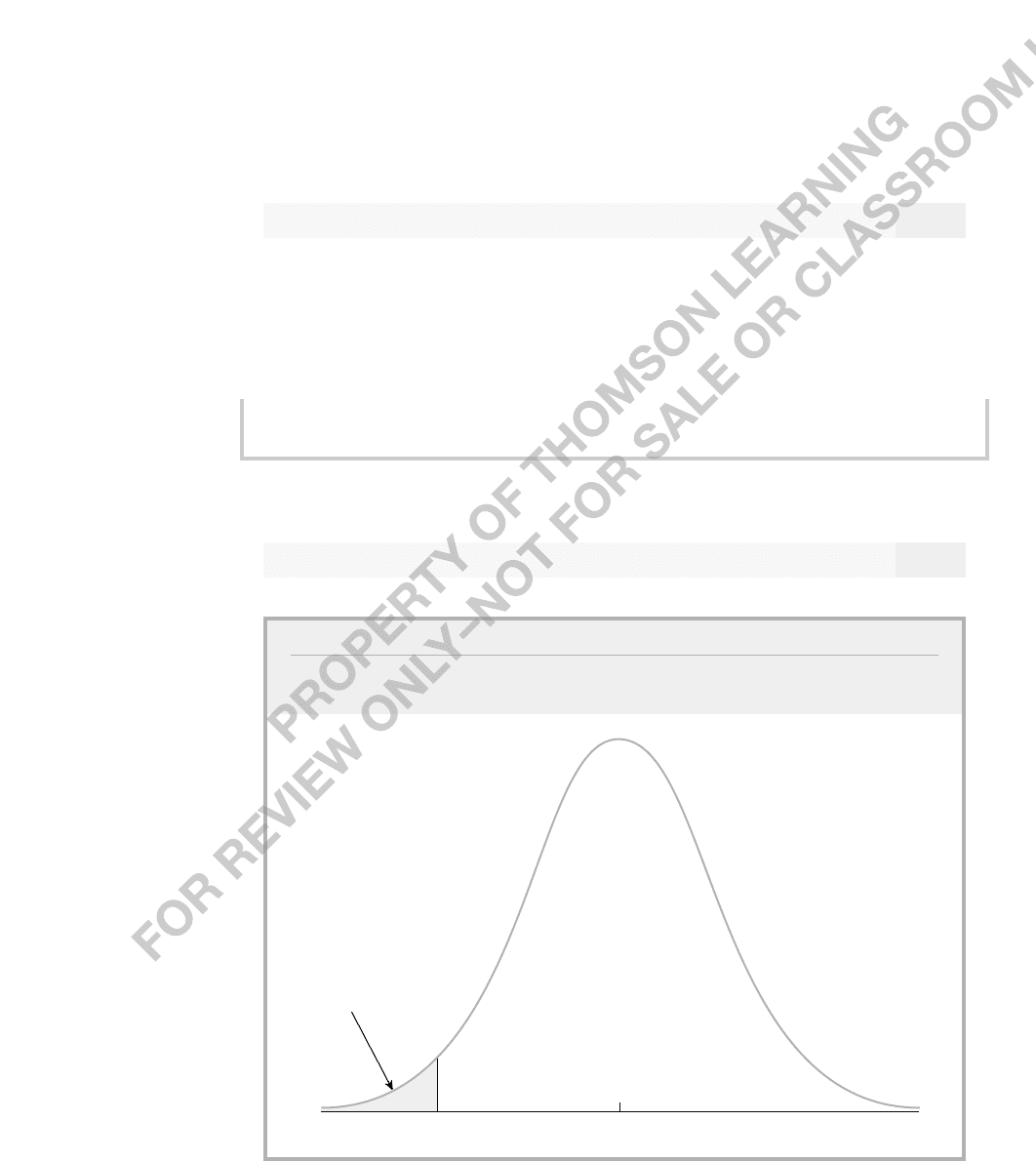
As an illustration, consider the problem of testing H
0
: m 0 in a Normal(m,s
2
) pop-
ulation. Our test statistic in this case is T
nY
¯
/S, and we assume that n is large enough
to treat T as having a standard normal distribution under H
0
. Suppose that the observed
value of T for our sample is t 1.52. (Note how we have skipped the step of choosing a
significance level.) Now that we have seen the value t, we can find the largest significance
level at which we would fail to reject H
0
. This is the significance level associated with
using t as our critical value. Because our test statistic T has a standard normal distribution
under H
0
, we have
p-value P(T 1.52H
0
) 1 (1.52) .065, (C.40)
where () denotes the standard normal cdf. In other words, the p-value in this example
is simply the area to the right of 1.52, the observed value of the test statistic, in a standard
normal distribution. See Figure C.7 for illustration.
Because p-value .065, the largest significance level at which we can carry out this
test and fail to reject is 6.5%. If we carry out the test at a level below 6.5% (such as at
5%), we fail to reject H
0
. If we carry out the test at a level larger than 6.5% (such as 10%),
we reject H
0
. With the p-value at hand, we can carry out the test at any level.
The p-value in this example has another useful interpretation: it is the probability that
we observe a value of T as large as 1.52 when the null hypothesis is true. If the null
hypothesis is actually true, we would observe a value of T as large as 1.52 due to chance
only 6.5% of the time. Whether this is small enough to reject H
0
depends on our tolerance
for a Type I error. The p-value has a similar interpretation in all other cases, as we
will see.
Generally, small p-values are evidence against H
0
, since they indicate that the
outcome of the data occurs with small probability if H
0
is true. In the previous example,
if t had been a larger value, say, t 2.85, then the p-value would be 1
(2.85) .002. This means that, if the null hypothesis were true, we would observe a
value of T as large as 2.85 with probability .002. How do we interpret this? Either we
obtained a very unusual sample or the null hypothesis is false. Unless we have a very small
tolerance for Type I error, we would reject the null hypothesis. On the other hand, a large
p-value is weak evidence against H
0
. If we had gotten t .47 in the previous example,
then p-value 1 (.47) .32. Observing a value of T larger than .47 happens with
probability .32, even when H
0
is true; this is large enough so that there is insufficient doubt
about H
0
, unless we have a very high tolerance for Type I error.
Appendix C Fundamentals of Mathematical Statistics 795

For hypothesis testing about a population mean using the t distribution, we need
detailed tables in order to compute p-values. Table G.2 only allows us to put bounds on
p-values. Fortunately, many statistics and econometrics packages now compute p-values
routinely, and they also provide calculation of cdfs for the t and other distributions used
for computing p-values.
EXAMPLE C.6
(Effect of Job Training Grants on Worker Productivity)
Consider again the Holzer et al. (1993) data in Example C.2. From a policy perspective, there
are two questions of interest. First, what is our best estimate of the mean change in scrap
rates, m? We have already obtained this for the sample of 20 firms listed in Table C.3: the
sample average of the change in scrap rates is 1.15. Relative to the initial average scrap rate
in 1987, this represents a fall in the scrap rate of about 26.3% (1.15/4.38 .263), which
is a nontrivial effect.
We would also like to know whether the sample provides strong evidence for an effect in
the population of manufacturing firms that could have received grants. The null hypothesis is
H
0
: m 0, and we test this against H
1
: m 0, where m is the average change in scrap rates.
Under the null, the job training grants have no effect on average scrap rates. The alternative
states that there is an effect. We do not care about the alternative m 0, so the null hypoth-
esis is effectively H
0
: m 0.
796 Appendix C Fundamentals of Mathematical Statistics
0
1.52
area = .065
= p-value
FIGURE C.7
The p-value when t 1.52 for the one-sided alternative µ > µ
0
.
Since y
¯
1.15 and se(y
¯
) .54, t 1.15/.54 2.13. This is below the 5% critical
value of 1.73 (from a t
19
distribution) but above the 1% critical value, 2.54. The p-value
in this case is computed as
p-value P(T
19
2.13),
(C.41)
where T
19
represents a t distributed random variable with 19 degrees of freedom. The inequal-
ity is reversed from (C.40) because the alternative has the form in (C.33). The probability in
(C.41) is the area to the left of 2.13 in a t
19
distribution (see Figure C.8).
Using Table G.2, the most we can say is that the p-value is between .025 and .01, but it
is closer to .025 (since the 97.5
th
percentile is about 2.09). Using a statistical package, such
as Stata, we can compute the exact p-value. It turns out to be about .023, which is reason-
able evidence against H
0
. This is certainly enough evidence to reject the null hypothesis that
the training grants had no effect at the 2.5% significance level (and therefore at the 5% level).
Computing a p-value for a two-sided test is similar, but we must account for the two-sided
nature of the rejection rule. For t testing about population means, the p-value is computed as
P(T
n1
t) 2P(T
n1
t),
(C.42)
Appendix C Fundamentals of Mathematical Statistics 797
0
area = p-value = .023
–2.13
FIGURE C.8
The p-value when t 2.13 with 19 degrees of freedom
for the one-sided alternative m<0.

where t is the value of the test statistic and T
n1
is a t random variable. (For large n,replace
T
n1
with a standard normal random variable.) Thus, compute the absolute value of the t
statistic, find the area to the right of this value in a t
n1
distribution, and multiply the area
by two.
For nonnormal populations, the exact p-value can be difficult to obtain. Nevertheless,
we can find asymptotic p-values by using the same calculations. These p-values are valid
for large sample sizes. For n larger than, say, 120, we might as well use the standard nor-
mal distribution. Table G.1 is detailed enough to get accurate p-values, but we can also
use a statistics or econometrics program.
EXAMPLE C.7
(Race Discrimination in Hiring)
Using the matched pair data from the Urban Institute (n 241), we obtained t 4.29. If
Z is a standard normal random variable, P(Z 4.29) is, for practical purposes, zero. In other
words, the (asymptotic) p-value for this example is essentially zero. This is very strong evidence
against H
0
.
SUMMARY OF HOW TO USE p-VALUES:
(i) Choose a test statistic T and decide on the nature of the alternative. This deter-
mines whether the rejection rule is t c, t c, or t c.
(ii) Use the observed value of the t statistic as the critical value and compute the cor-
responding significance level of the test. This is the p-value. If the rejection rule is of the
form t c, then p-value P(T t). If the rejection rule is t c, then p-value P(T
t); if the rejection rule is t c, then p-value P(T t).
(iii) If a significance level
has been chosen, then we reject H
0
at the 100
% level
if p-value
. If p-value
, then we fail to reject H
0
at the 100
% level. Therefore,
it is a small p-value that leads to rejection.
The Relationship between Confidence Intervals
and Hypothesis Testing
Because contructing confidence intervals and hypothesis tests both involve probability state-
ments, it is natural to think that they are somehow linked. It turns out that they are. After a
confidence interval has been constructed, we can carry out a variety of hypothesis tests.
The confidence intervals we have discussed are all two-sided by nature. (In this text,
we will have no need to construct one-sided confidence intervals.) Thus, confidence inter-
vals can be used to test against two-sided alternatives. In the case of a population mean,
the null is given by (C.31), and the alternative is (C.34). Suppose we have constructed a
95% confidence interval for m. Then, if the hypothesized value of m under H
0
, m
0
, is not
in the confidence interval, then H
0
: m m
0
is rejected against H
1
: m m
0
at the 5% level.
798 Appendix C Fundamentals of Mathematical Statistics

If m
0
lies in this interval, then we fail to reject H
0
at the 5% level. Notice how any value
for m
0
can be tested once a confidence interval is constructed, and since a confidence inter-
val contains more than one value, there are many null hypotheses that will not be rejected.
EXAMPLE C.8
(Training Grants and Worker Productivity)
In the Holzer et al. example, we constructed a 95% confidence interval for the mean change
in scrap rate m as [2.28,.02]. Since zero is excluded from this interval, we reject H
0
: m
0 against H
1
: m 0 at the 5% level. This 95% confidence interval also means that we fail to
reject H
0
: m 2 at the 5% level. In fact, there is a continuum of null hypotheses that are
not rejected given this confidence interval.
Practical versus Statistical Significance
In the examples covered so far, we have produced three kinds of evidence concerning
population parameters: point estimates, confidence intervals, and hypothesis tests. These
tools for learning about population parameters are equally important. There is an under-
standable tendency for students to focus on confidence intervals and hypothesis tests
because these are things to which we can attach confidence or significance levels. But
in any study, we must also interpret the magnitudes of point estimates.
The sign and magnitude of y
–
determine its practical significance and allow us to dis-
cuss the direction of an intervention or policy effect, and whether the estimated effect is
“large” or “small.” On the other hand, statistical significance of y
–
depends on the mag-
nitude of its t statistic. For testing H
0
: m 0, the t statistic is simply t y
–
/se(y
–
). In other
words, statistical significance depends on the ratio of y
–
to its standard error. Consequently,
a t statistic can be large because y
–
is large or se(y
–
) is small. In applications, it is impor-
tant to discuss both practical and statistical significance, being aware that an estimate can
be statistically significant without being especially large in a practical sense. Whether an
estimate is practically important depends on the context as well as on one’s judgment, so
there are no set rules for determining practical significance.
EXAMPLE C.9
(Effect of Freeway Width on Commute Time)
Let Y denote the change in commute time, measured in minutes, for commuters in a metro-
politan area from before a freeway was widened to after the freeway was widened. Assume
that Y ~ Normal(m,s
2
). The null hypothesis that the widening did not reduce average com-
mute time is H
0
: m 0; the alternative that it reduced average commute time is H
1
: m 0.
Suppose a random sample of commuters of size n 900 is obtained to determine the effec-
tiveness of the freeway project. The average change in commute time is computed to be y
¯
3.6, and the sample standard deviation is s 32.7; thus, se(y
¯
) 32.7/
900 1.09.
Appendix C Fundamentals of Mathematical Statistics 799

The t statistic is t 3.6/1.09 3.30, which is very statistically significant; the p-value is
about .0005. Thus, we conclude that the freeway widening had a statistically significant effect
on average commute time.
If the outcome of the hypothesis test is all that were reported from the study, it would be
misleading. Reporting only statistical significance masks the fact that the estimated reduction
in average commute time, 3.6 minutes, is pretty meager. To be up front, we should report the
point estimate of 3.6, along with the significance test.
Finding point estimates that are statistically significant without being practically sig-
nificant can occur when we are working with large samples. To discuss why this happens,
it is useful to have the following definition.
TEST CONSISTENCY. A consistent test rejects H
0
with probability approaching one as
the sample size grows whenever H
1
is true.
Another way to say that a test is consistent is that, as the sample size tends to infinity, the
power of the test gets closer and closer to unity whenever H
1
is true. All of the tests we
cover in this text have this property. In the case of testing hypotheses about a population
mean, test consistency follows because the variance of Y
¯
converges to zero as the sample
size gets large. The t statistic for testing H
0
: m 0 is T Y
¯
/(S/
n). Since plim(Y
¯
) m
and plim(S) s, it follows that if, say, m 0, then T gets larger and larger (with high
probability) as n → . In other words, no matter how close m is to zero, we can be almost
certain to reject H
0
: m 0 given a large enough sample size. This says nothing about
whether m is large in a practical sense.
C.7 Remarks on Notation
In our review of probability and statistics here and in Appendix B, we have been careful
to use standard conventions to denote random variables, estimators, and test statistics. For
example, we have used W to indicate an estimator (random variable) and w to denote a
particular estimate (outcome of the random variable W ). Distinguishing between an esti-
mator and an estimate is important for understanding various concepts in estimation and
hypothesis testing. However, making this distinction quickly becomes a burden in econo-
metric analysis because the models are more complicated: many random variables and
parameters will be involved, and being true to the usual conventions from probability and
statistics requires many extra symbols.
In the main text, we use a simpler convention that is widely used in econometrics. If
u is a population parameter, the notation u
ˆ
(“theta hat”) will be used to denote both an
estimator and an estimate of u. This notation is useful in that it provides a simple way of
attaching an estimator to the population parameter it is supposed to be estimating. Thus,
if the population parameter is
, then
ˆ
denotes an estimator or estimate of
; if the param-
eter is s
2
, s
ˆ
2
is an estimator or estimate of s
2
; and so on. Sometimes, we will discuss two
estimators of the same parameter, in which case we will need a different notation, such as
u
˜
(“theta tilde”).
800 Appendix C Fundamentals of Mathematical Statistics

Although dropping the conventions from probability and statistics to indicate estima-
tors, random variables, and test statistics puts additional responsibility on you, it is not a
big deal once the difference between an estimator and an estimate is understood. If we are
discussing statistical properties of u
ˆ
—such as deriving whether or not it is unbiased or
consistent—then we are necessarily viewing u
ˆ
as an estimator. On the other hand, if we
write something like u
ˆ
1.73, then we are clearly denoting a point estimate from a given
sample of data. The confusion that can arise by using u
ˆ
to denote both should be minimal
once you have a good understanding of probability and statistics.
SUMMARY
We have discussed topics from mathematical statistics that are heavily relied upon in
econometric analysis. The notion of an estimator, which is simply a rule for combining
data to estimate a population parameter, is fundamental. We have covered various proper-
ties of estimators. The most important small sample properties are unbiasedness and effi-
ciency, the latter of which depends on comparing variances when estimators are unbiased.
Large sample properties concern the sequence of estimators obtained as the sample size
grows, and they are also depended upon in econometrics. Any useful estimator is consis-
tent. The central limit theorem implies that, in large samples, the sampling distribution of
most estimators is approximately normal.
The sampling distribution of an estimator can be used to construct confidence intervals.
We saw this for estimating the mean from a normal distribution and for computing approx-
imate confidence intervals in nonnormal cases. Classical hypothesis testing, which requires
specifying a null hypothesis, an alternative hypothesis, and a significance level, is carried
out by comparing a test statistic to a critical value. Alternatively, a p-value can be computed
that allows us to carry out a test at any significance level.
KEY TERMS
Appendix C Fundamentals of Mathematical Statistics 801
Alternative Hypothesis
Asymptotic Normality
Bias
Biased Estimator
Central Limit Theorem
(CLT)
Confidence Interval
Consistent Estimator
Consistent Test
Critical Value
Estimate
Estimator
Hypothesis Test
Inconsistent
Power of a Test
Practical Significance
Probability Limit
p-Value
Random Sample
Rejection Region
Sample Average
Sample Correlation
Coefficient
Sample Covariance
Sample Standard Deviation
Sample Variance
Sampling Distribution
Sampling Variance
Interval Estimator
Law of Large Numbers
(LLN)
Least Squares Estimator
Maximum Likelihood
Estimator
Mean Squared Error (MSE)
Method of Moments
Minimum Variance
Unbiased Estimator
Null Hypothesis
One-Sided Alternative
One-Tailed Test
Population

PROBLEMS
C.1 Let Y
1
, Y
2
, Y
3
, and Y
4
be independent, identically distributed random variables
from a population with mean m and variance s
2
. Let Y
¯
(Y
1
Y
2
Y
3
Y
4
) denote
the average of these four random variables.
(i) What are the expected value and variance of Y
¯
in terms of m and s
2
?
(ii) Now, consider a different estimator of m:
W Y
1
Y
2
Y
3
Y
4
.
This is an example of a weighted average of the Y
i
. Show that W is also
an unbiased estimator of m. Find the variance of W.
(iii) Based on your answers to parts (i) and (ii), which estimator of m do you
prefer, Y
¯
or W?
C.2 This is a more general version of Problem C.1. Let Y
1
, Y
2
,…,Y
n
be n pairwise uncor-
related random variables with common mean m and common variance s
2
. Let Y
¯
denote
the sample average.
(i) Define the class of linear estimators of m by
W
a
a
1
Y
1
a
2
Y
2
… a
n
Y
n
,
where the a
i
are constants. What restriction on the a
i
is needed for W
a
to
be an unbiased estimator of m?
(ii) Find Var(W
a
).
(iii) For any numbers a
1
,a
2
,…,a
n
, the following inequality holds: (a
1
a
2
… a
n
)
2
/n a
1
2
a
2
2
… a
n
2
. Use this, along with parts (i) and
(ii), to show that Var(W
a
) Var(Y
¯
) whenever W
a
is unbiased, so that Y
¯
is
the best linear unbiased estimator. [Hint: What does the inequality become
when the a
i
satisfy the restriction from part (i)?]
C.3 Let Y
¯
denote the sample average from a random sample with mean m and variance
s
2
. Consider two alternative estimators of m: W
1
[(n 1)/n]Y
¯
and W
2
Y
¯
/2.
(i) Show that W
1
and W
2
are both biased estimators of m and find the biases.
What happens to the biases as n → ? Comment on any important differ-
ences in bias for the two estimators as the sample size gets large.
(ii) Find the probability limits of W
1
and W
2
. {Hint: Use Properties PLIM.1
and PLIM.2; for W
1
, note that plim [(n 1)/n] 1.} Which estimator is
consistent?
(iii) Find Var(W
1
) and Var(W
2
).
(iv) Argue that W
1
is a better estimator than Y
¯
if m is “close” to zero. (Consider
both bias and variance.)
1
2
1
4
1
8
1
8
1
4
802 Appendix C Fundamentals of Mathematical Statistics
Type II Error
Unbiased Estimator
Significance Level
Standard Error
Statistical Significance
t Statistic
Test Statistic
Two-Sided Alternative
Two-Tailed Test
Type I Error

C.4 For positive random variables X and Y, suppose the expected value of Y given X is
E(YX) uX. The unknown parameter u shows how the expected value of Y changes
with X.
(i) Define the random variable Z Y/X. Show that E(Z) u. [Hint: Use Prop-
erty CE.2 along with the law of iterated expectations, Property CE.4. In
particular, first show that E(ZX) u and then use CE.4.]
(ii) Use part (i) to prove that the estimator W
1
n
1
n
i1
(Y
i
/X
i
) is unbiased
for u,where {(X
i
,Y
i
): i 1,2, …, n} is a random sample.
(iii) Explain why the estimator W
2
Y
¯
/X
¯
,where the overbars denote sample
averages, is not the same as W
1
. Nevertheless, show that W
2
is also unbi-
ased for u.
(iv) The following table contains data on corn yields for several counties in
Iowa. The USDA predicts the number of hectares of corn in each county
based on satellite photos. Researchers count the number of “pixels” of corn
in the satellite picture (as opposed to, for example, the number of pixels of
soybeans or of uncultivated land) and use these to predict the actual num-
ber of hectares. To develop a prediction equation to be used for counties in
general, the USDA surveyed farmers in selected counties to obtain corn
yields in hectares. Let Y
i
corn yield in county i and let X
i
number of
corn pixels in the satellite picture for county i. There are n 17 observa-
tions for eight counties. Use this sample to compute the estimates of u
devised in parts (ii) and (iii). Are the estimates similar?
Plot Corn Yield Corn Pixels
1 165.76 374
2 96.32 209
3 76.08 253
4 185.35 432
5 116.43 367
6 162.08 361
7 152.04 288
8 161.75 369
9 92.88 206
10 149.94 316
Appendix C Fundamentals of Mathematical Statistics 803
(continued)

Plot Corn Yield Corn Pixels
11 64.75 145
12 127.07 355
13 133.55 295
14 77.70 223
15 206.39 459
16 108.33 290
17 118.17 307
C.5 Let Y denote a Bernoulli(u) random variable with 0 u 1. Suppose we are inter-
ested in estimating the odds ratio,
u/(1 u), which is the probability of success over
the probability of failure. Given a random sample {Y
1
,…,Y
n
}, we know that an unbiased
and consistent estimator of u is Y
¯
, the proportion of successes in n trials. A natural esti-
mator of
is G Y
¯
/(1 Y
¯
), the proportion of successes over the proportion of failures
in the sample.
(i) Why is G not an unbiased estimator of
?
(ii) Use PLIM.2(iii) to show that G is a consistent estimator of
.
C.6 You are hired by the governor to study whether a tax on liquor has decreased aver-
age liquor consumption in your state. You are able to obtain, for a sample of individuals
selected at random, the difference in liquor consumption (in ounces) for the years before
and after the tax. For person i who is sampled randomly from the population, Y
i
denotes
the change in liquor consumption. Treat these as a random sample from a Normal(m,s
2
)
distribution.
(i) The null hypothesis is that there was no change in average liquor con-
sumption. State this formally in terms of m.
(ii) The alternative is that there was a decline in liquor consumption; state the
alternative in terms of m.
(iii) Now, suppose your sample size is n 900 and you obtain the estimates
y
¯
32.8 and s 466.4. Calculate the t statistic for testing H
0
against H
1
;
obtain the p-value for the test. (Because of the large sample size, just use
the standard normal distribution tabulated in Table G.1.) Do you reject H
0
at the 5% level? At the 1% level?
(iv) Would you say that the estimated fall in consumption is large in
magnitude? Comment on the practical versus statistical significance of this
estimate.
804 Appendix C Fundamentals of Mathematical Statistics
