Wilkinson D.J. Stochastic Modelling for Systems Biology
Подождите немного. Документ загружается.


14
INTRODUCTION
TO
BIOLOGICAL
MODELLING
I - - - - - - - - - - - -
-.
,
'f
.---------
I
v
p
P2
~----.
: r
~
p q
g
DNA
Figure
1.
7 A very simple
TTWdel
of
a prokaryotic auto-regulatory gene network. Here dimers
of
a protein P
coded
for
by
a gene g repress their own transcription
by
binding to a regulatory
region q upstream
of
g and downstream
of
the prolTWter p.
transport points. A more realistic model would therefore be
Tn
+ N
--+
Tn
· N
Tn
• N
--+
Tc
+
N,
where N denotes the set
of
available mRNA transport points embedded in the outer
shell
of
the cell nucleus. In fact, this system is very closely related to the Michaelis-
Menten enzyme kinetic system that will
be
examined in more detail later in the book.
Here, the transport points behave like an enzyme whose abundance limits the flow
from
Tn
to
rc.
1.5. 7 Prokaryotic auto-regulation
Now
that
we
have seen how to generate very simple models
of
key processes involved
in gene expression
and
regulation,
we
can
put
them together in the form
of
a simple
prokaryotic auto-regulatory network.
Figure 1.7 illustrates a simple gene expression auto-regulation mechanism often
present in prokaryotic
gene
networks. Here, dimers
of
the protein P coded for by the
gene
g repress their
own
transcription
by
binding to a (repressive) regulatory region
upstream
of
g.
MODELLING GENETIC AND BIOCHEMICAL NETWORKS
~
a--------·
Ia\
I I
~
1---•
I
:---·
. •
I
Lactose
A
I
I
.--------·
I
I .
rl
A
I
..
---.
I
RNAP
z
y
A
•••
A
A
},.
I
-I
·-·
.-
-·
@
!Qi@i.....
DNA
p o z y a
15
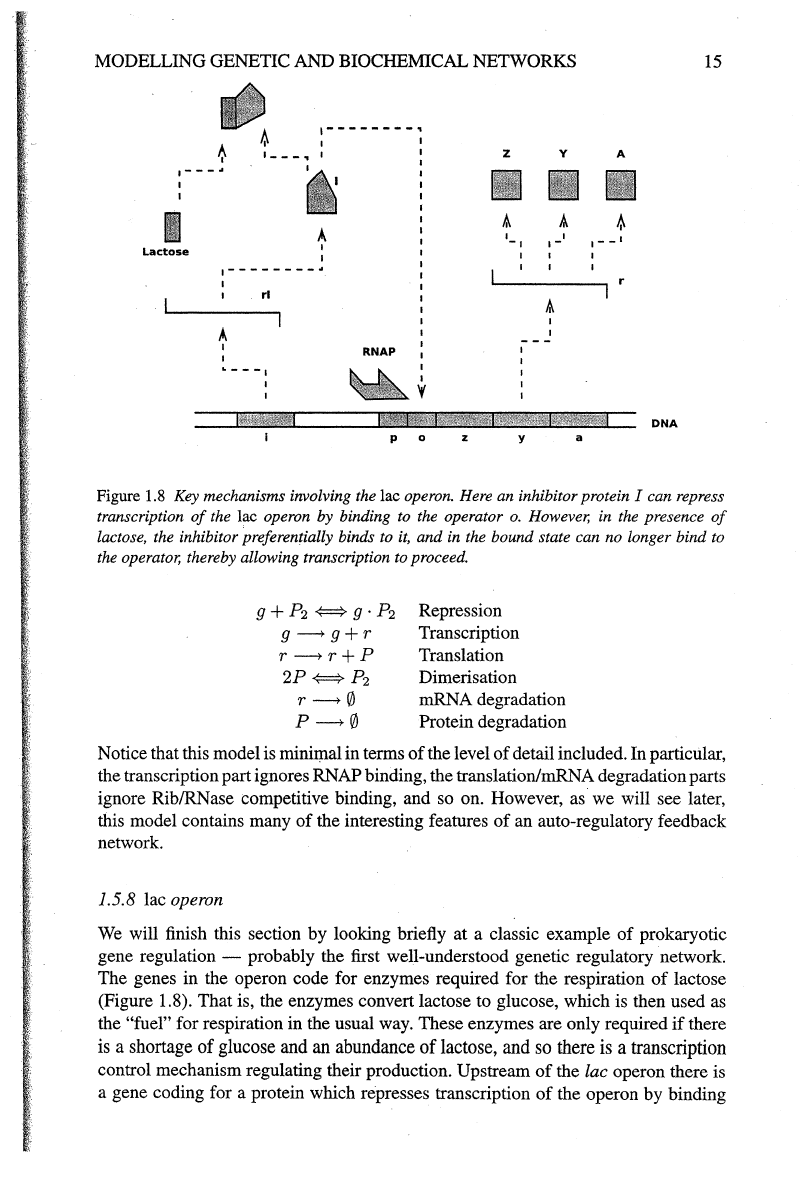
Figure 1.8
Key
mechanisms involving the lac operon. Here an inhibitor protein I can repress
transcription
of
the lac operon by binding to the operator
o.
However, in the presence
of
lactose, the inhibitor preferentially binds to
it,
and in the bound state can no longer bind to
the operator, thereby allowing transcription to proceed.
g + P
2
{:::::>
g ·
P2
Repression
g
~
g + r Transcription
r
~
r + P Translation
2P
{:::::>
P
2
Dimerisation
r
~
0 mRNA degradation
P
~
0 Protein degradation
Notice that this model is
~in
terms
of
the level
of
detail included.
In
particlilar,
the transcription part ignores RNAP binding, the translation/mRNA degradation parts
ignore Rib/RNase competitive binding, and so on. However,
as
we will see later,
this model contains many
of
the interesting features
of
an auto-reglilatory feedback
network.
1.5.8 lac
operon
We
will finish this section by looking briefly at a classic example of prokaryotic
gene regulation - probably the first well-understood genetic regulatory network.
The genes in the operon code for enzymes required for the respiration
of
lactose
(Figure 1.8). That is, the enzymes convert lactose to glucose, which is then used as
the
"fuel" for respiration in the usual way. These enzymes are only required
if
there
is
a
shortage
of
glucose
and
an
abundance
of
lactose,
and
so
there
is
a
transcription
control mechanism regulating their production. Upstream
of
the lac operon there is
a gene coding for a protein which represses transcription
of
the operon by binding

16
INTRODUCTION TO BIOLOGICAL MODELLING
to the DNA just downstream
of
the RNAP binding site. Under normal conditions
(absence
of
lactose), transcription
of
the lac operon is turned off. However, in the
presence
of
lactose, the inhibitor protein preferentially binds to lactose, and in the
bound state can no longer bind to the DNA. Consequently, the repression
of
tran-
scription is removed, and production
of
the required enzymes can take place.
We
can
represent this with the following simple
set
of
reactions:
i ----> i +
r1
r1
---->
r1
+I
I + Lactose
¢==?
I · Lactose
I+o¢=?I·o
o + RNAP
¢==?
RNAP · o
RNAP · o ----> o + RNAP + r
r---->r+A+Y+Z
Lactose + Z ----> Z.
Here, i represents the gene for the inhibitor protein,
r
1
the associated mRNA, and
I the inhibitor protein itself. The lac operon is denoted o and is treated as a single
entity from a modelling viewpoint. The mRNA transcript from the operon is denoted
by
r,
and this codes for all three lac proteins. The final reaction represents the trans-
formation
of
lactose to something not directly relevant to the regulation mechanism.
Again, this system is fairly minimal
in
terms
of
the detail included, and all
of
the
degradation reactions have been omitted, along with what happens to lactose once it
has been acted on by ,B-galactosidase (
Z).
In fact, there is also another mechanism we
have not considered here that ensures that transcription
of
the operon will only occur
when there is a shortage
of
glucose (as respiration
of
glucose is always preferred).
1.6 Modelling higher-level systems
We have concentrated so far on fairly low-level biochemical models where the con-
cept
of
modelling with "chemical reactions" is perhaps most natural. However, it is
important to recognise that we use the notation
of
chemical reactions simply to de-
scribe things that combine and the things that they produce, and that this framework
can
be
used to model higher-level phenomena in a similar way.
In
Section
1.3
the lin-
ear birth-death process was introduced as a model for the number
of
bacteria present
in a colony. We can use our chemical reaction notation to capture the qualitative
structure
of
this model.
X---->
2X
X----+
0
The first equation represents "birth"
of
new bacteria and the second "death." There
are many possible extensions
of
this simple model, including the introduction
of
im-
migration
of
new bacteria from another source and emigration
of
bacteria to another
source.

EXERCISES
17
The
ahove model represents a model for a "population"
of
individuals (here the
individuals are bacteria), and it is possible to extend such models to populations
involving more than one
"species." Consider the Lotka-Volterra predator prey model
for two interacting species:
Y1
~2Y1
Y1
+
Y2
~
2Y2
Y2~0.
Again, this is not a real reaction system in the strictest sense, but it is interesting and
useful, as
it
is the simplest model exhibiting the kind
of
non-linear auto-regulatory
feedback behaviour considered earlier. Also, as it only involves two species and three
reactions, it is relatively easy to work with without getting lost in detail. Here,
Y
1
represents a "prey" species (such as rabbits) and Y
2
represents a "predator" species
(such as foxes).§ The first reaction is a simple representation
of
prey reproduction.
The second reaction is an attempt to capture predator-prey interaction (consumption
of
prey by predator, in turn influencing predator reproduction rate). The third reaction
represents death
of
predators due
to
natural causes. We will revisit this model in
greater detail in later chapters.
1.7 Exercises
1.
Write out a more detailed and realistic model for the simple auto-regulatory net-
work considered in Section 1.5.7. Include RNAP binding, Rib/RNase competitive
binding, and so on.
2.
Consider the lac operon model from Section 1.5.8.
(a) First add more detail to the model, as in the previous exercise.
(b) Look up the
,@-galactosidase pathway and add detail from this to the model.
(c) Find details
of
the additional regulation mechanism mentioned that ensures
lactose
is
only respired in an absence
of
glucose and try to incorporate that into
the model.
1.8 Further reading
See Bower & Bolouri (2000) for more detailed information on modelling, and the dif-
ferent possible approaches to modelling genetic and biochemical networks. Kitano
(2001) gives a more general overview
of
biological modelling and systems biology.
McAdams
& Arkin (1997) and Arkin
et
al. (1998) explore biological modelling in
the context
of
the discrete stochastic models we will consider later. The lac operon
is discussed in many biochemistry texts, including Stryer (1988). The original ref-
erences for the Lotka-Volterra predator-prey models are Lotka (1925) and Volterra
(1926).
§ Note that the use
of
reactions to model the interaction
of
"species" in a population dynamics context
explains the use of the term
"species" to refer to a particular type
of
chemical molecule in a set
of
coupled chemical reactions.

18
INTRODUCfiON
TO
BIOLOGICAL MODELLING
The
website associated with this
book,
contains a range
of
links to online infor-
mation
of
relevance to the various chapters
of
the book. Now would probably be a
good time to have a quick look
at
it and "bookmark"
it
for future reference.
,URL:http://www.staff.ncl.ac.uk/d.j.wilkinson/smfsb/

CHAPTER2
Representation
of
biochemical networks
2.1 Coupled chemical reactions
As
was illustrated in the first chapter, a powerful and flexible way to specify a model
is to simply write down a list of reactions corresponding to the system
of
interest.
Note, however, that the reactions themselves specify only the qualitative structure
of
a model and must be augmented with additional information before they can be
used to carry out a dynamic simulation on a computer. The model is completed by
specifying the rate
of
every reaction, together with initial amounts
of
each reacting
species.
Reconsider the auto-regulation example from Section 1.5.
7:
g+P2
~g·P2
g~g+r
r~r+P
2P~P2
r~0,
P~0.
Although only six reactions are listed, there are actually eight,
as
two are reversible.
Each
of
those eight reactions must have a rate law associated with it.
We
will de-
fer discussion
of
rate laws until Chapter
6.
For now, it is sufficient to know that the
rate laws quantify the propensity of particular reactions to take place and are likely
to
depend on the current amounts of available reactants. In addition there must be
an initial amount for each
of
the
five
chemical species involved: g · P
2
,
g,
r,
P,
and
P2.
Given the reactions, the rate laws, and the initial amounts (together with some as-
sumptions regarding the underlying kinetics, which are generally not regarded
as
part
of
the model), the model is specified and can in principle be simulated dynamically
on a computer.
The problem is that even this short list
of
reactions is hard to understand on its
own, whereas the simple biologist's diagram (Figure 1.7) is not sufficiently detailed
and explicit to completely define the model. What is needed is something between
the biologist's diagram and the list
of
reactions.
2.2 Graphical representations
2.2.1 Introduction
One way
to
begin to understand a reaction network is to display it
as
a pathway
diagram
of
some description. The diagram in Figure 2.1 is similar to that used by
19

20
REPRESENTATION OF
BIOCHEMICAL NETWORKS
Figure
2.1
A simple
graph
of
the
auto-regulatory
reaction
network
some biological model-building tools such as JDesigner, which is part
of
the Systems
Biology Workbench (SBW). *
Such a diagram is easier to understand than the reaction list, yet it contains the
same amount
of
information and hence could be used to generate a reaction list. Note
that auto-regulation by its very nature implies a
"loop" in the reaction network, which
is very obvious and explicit in the associated diagram.
One possible problem with
diagrams such as this, however, is the fact that it can sometimes be hard to distinguish
which are the reactants and which are the products in any given reaction (particularly
in
large complex networks), and this can make it difficult to understand the
flow
of
species through the network. Also, the presence
of
"branching" and "looping" arcs
makes them slightly unnatural to work with directly in a mathematical sense.
Such problems are easily overcome by formalising the notion
of
pathway diagrams
using the concept
of
a graph (here we mean the mathematical notion
of
a graph, not
the idea
of
the graph
of
a function), where each node represents either a chemical
species or a reaction, and arcs are used to indicate reaction pathways. In order to
make this explicit, some elementary graph theoretic notation is helpful.
2.2.2 Graph theory
Definition 2.1 A directed graph
or
digraph, g is a tuple
(V,
E),
where V = { v
1
,
...
,
vn} is a set
of
nodes (or vertices)
and
E = {
(Vi,
Vj
)I
vi,
Vj
E V,
Vi
-+
Vj}
is a set
of
directed edges (or arcs), where we use the notation
Vi
-+
Vj
if
and
only
if
there is
a directed edge from node
Vi
to
Vj·
So the graph shown in Figure 2.2 has mathematical representation
g =
({a,b,c},
{(a,c), (c,b)}).
* Software web links tend to go out
of
date rather quickly, so a regularly updated list is available from
the book's web page.

PETRI NETS
21
Figure
2.2
A
simple
digraph
Definition 2.2 A graph
is
described as simple
if
there do
not
exist edges
of
the form
(Vi,
Vi)
and there are no repeated edges. A bipartite graph
is
a simple graph where
the nodes are partitioned into two distinct subsets
vl
and
v2
(so that v =
vl
u
v2
and
vl
n
v2
=
0)
such that there are no arcs joining nodes from the same subset.
Referring back to the previous example, the partition V
1
=
{a,
b},
V2
= { c} gives
a bipartite graph
(Q
is said to
be
bipartite over the partition), and the partition
Vi
=
{a},
% = {b, c} does not (as the edge (
c,
b)
would then
be
forbidden). A weighted
graph is a graph which has (typically positive) numerical values associated with each
edge.
2.2.3 Reaction graphs
It
turns out that it is very natural to represent sets
of
coupled chemical reactions using
weighted bipartite graphs where the nodes are partitioned into two sets representing
the species and reactions.
An arc from a species node to a reaction node indicates that
the species is a reactant for that reaction, and an arc from a reaction node to a species
node indicates that the species is a product
of
the reaction. The weights associated
with the arcs represent the stoichiometries associated with the reactants and products.
There is a very strong correspondence between reaction graphs modelled this way,
and the theory
of
Petri nets, which are used extensively in computing science for a
range
of
modelling problems. A particular advantage
of
Petri net theory is that it is
especially well suited to the discrete-event stochastic simulation models this book is
mainly concerned with.
It
is therefore helpful to have a basic familiarity with Petri
nets and their application to biological modelling.
2.3
Petri nets
2.3.1 Introduction
Petri nets are a mathematical framework for systems modelling together with
an
associated graphical representation. Goss & Peccoud (1998) were among the first
tO
use stochastic Petri nets for biological modelling. Recent reviews
of
the use
of
Petri
nets for biological modelling include Pinney, Westhead & McConkey (2003) and
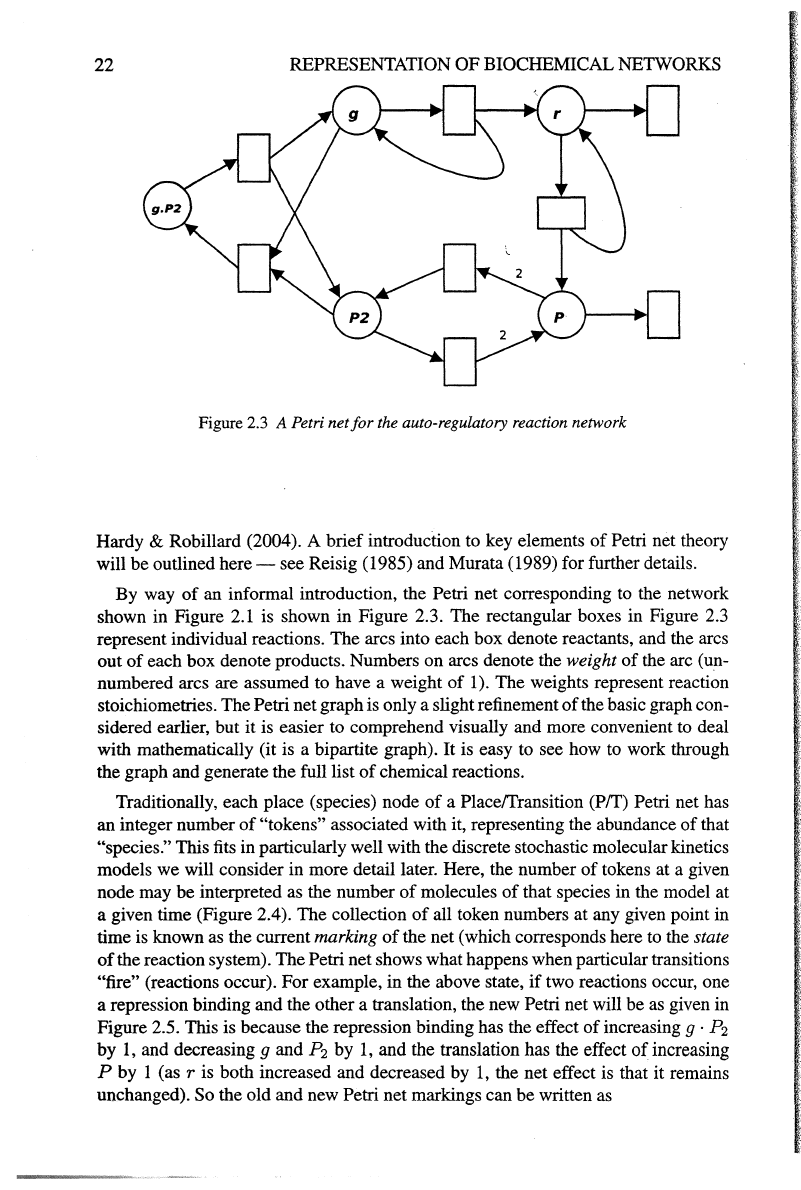
22
REPRESENTATION
OF BIOCHEMICAL NE'IWORKS
Figure
2.3
A Petri
net
for
the auto-regulatory reaction network
Hardy & Robillard (2004). A
brief
introduction to key elements
of
Petri net theory
will
be
outlined here - see Reisig ( 1985) and Murata ( 1989) for further details.
By
way
of
an informal introduction, the Petri net corresponding to the network
shown in Figure 2.1 is shown in Figure 2.3.
The
rectangular boxes in Figure 2.3
represent individual reactions.
The
arcs into each
box
denote reactants, and the arcs
out
of
each box denote products. Numbers
on
arcs denote the weight
of
the arc (un-
numbered arcs are assumed to have a weight
of
1).
The
weights represent reaction
stoichiometries.
The
Petri
net
graph
is
only a slight refinement
of
the basic graph con-
sidered earlier,
but
it
is easier to comprehend visually and more convenient to deal
with mathematically (it is a bipartite graph).
It
is
easy to see how to work through
the graph and generate the
full list
of
chemical reactions.
Traditionally, each place (species) node
of
a Place/Transition
(Pff)
Petri net has
an
integer number
of
"tokens" associated with it, representing the abundance
of
that
"species." This fits in particularly well with the discrete stochastic molecular kinetics
models
we
will consider
in
more detail later. Here, the number
of
tokens at a given
node may
be
interpreted as the number
of
molecules
of
that species in the model at
a given time (Figure 2.4).
The
collection
of
all token numbers at any given point in
time is known as the current
marking
of
the
net
(which corresponds here to the state
of
the reaction system).
The
Petri
net
shows what happens when particular transitions
''fire" (reactions occur).
For
example, in the above state,
if
two reactions occur, one
a repression binding and
the
other a translation, the new Petri net will
be
as given in
Figure 2.5. This
is
because the repression binding has the effect
of
increasing g · P
2
by
1, and decreasing g
and
P
2
by
1, and the translation has the effect
of
increasing
P
by
1 (as r
is
both increased
and
decreased by
1,
the
net
effect is that
it
remains
unchanged).
So
the old
and
new Petri
net
markings can
be
written as

PETRI
NETS
23
Figure 2.4 A Petri
net
labelled with tokens
Figure 2.5 A Petri
net
with new numbers
of
tokens after reactions have taken place
Species No. tokens Species No. tokens
g ·
Pz
0
g·Pz
1
g
1
and
g
0
r 2 r
2
p
10
p
11
Pz
12
Pz
11
