Wai-Fah Chen.The Civil Engineering Handbook
Подождите немного. Документ загружается.


© 2003 by CRC Press LLC
e
at
te
at
(n = 1, 2, 3, K)
z-Transform
For the real-valued sequence {f (k)} and complex variable z, the z-transform, F (z) = Z{f (k)}, is defined by
For example, the sequence f (k) = 1, k = 0, 1, 2, K, has the z-transform
Angles are measured in degrees or radians: 180° = π radians; 1 radian = 180°/π degrees.
The trigonometric functions of 0°, 30°, 45°, and integer multiples of these are directly computed.
Trigonometric Identities
0° 30° 45° 60° 90° 120° 135° 150° 180°
sin 0 1 0
cos 1 0 –1
tan 0 1 ∞ – 1 0
ctn ∞ 1 0 – 1 ∞
sec 1 2 ∞ – 2 – 1
csc ∞ 2 1 2 ∞
1
sa–
----------
tatcos
s
2
a
2
–
s
2
a
2
+()
2
----------------------
1
sa–()
2
-----------------
e
at
btsin
b
sa–()
2
b
2
+
-----------------------------
t
n 1–
e
at
n 1–()!
------------------
1
sa–()
n
-----------------
e
at
btcos
sa–
sa–()
2
b
2
+
-----------------------------
t
x
Γ x 1+()
---------------------
1
s
x 1+
---------
, x 1–>
atsin
t
-------------
Arc
a
s
--
tan
atsin
a
s
2
a
2
+
---------------
asinh t
t
-----------------
1
2
--
sa+
sa–
-----------
e
log
acos t
s
s
2
a
2
+
---------------
Zfk(){}Fz() fk()z
k–
k 0=
∞
∑
==
Fz() 1 z
1–
z
2–
z
3–
L z
k–
L+++ ++=
1
2
--
2
2
-------
3
2
-------
3
2
-------
2
2
-------
1
2
--
3
2
-------
2
2
-------
1
2
--
1
2
--–
2
2
-------–
3
2
-------–
3
3
-------
3 3–
3
3
-------–
3
3
3
-------
3
3
-------–
3–
23
3
----------
2
2–
23
3
----------–
2
23
3
----------
23
3
----------
2
Asin
1
Acsc
-------------=
Acos
1
Asec
-------------=

© 2003 by CRC Press LLC
Defining z = e
sT
gives
which is the z-transform of the sampled signal U(kT).
Properties
Linearity:
Right-shifting property:
Left-shifting property:
Time scaling:
Multiplication by k:
Initial value:
Final value:
Convolution:
z-Transforms of Sampled Functions
f(k)
1
kT
L U
*
t(){} UkT()z
k–
k 0=
∞
∑
=
Zaf
1
k() bf
2
k()+{ } aZ f
1
k(){}bZ f
2
k(){}+ aF
1
z() bF
2
z()+= =
Zfkn–(){}z
n–
Fz()=
Zfkn+(){}z
n
Fz() fk()z
nk–
k 0=
n 1–
∑
–=
Za
k
fk(){}Fz a⁄()=
Zkfk(){}zdF z()dz⁄–=
f 0() 1 z
1–
–()Fz()
z
∞
→
lim F
∞
()= =
fk()
k ∞→
lim 1 z
1–
–()
z 1→
lim Fz()=
Zf
1
k()
*
f
2
k(){ } F
1
z()F
2
z()=
ZfkT(){}Fz()=
1 at k else 0; z
k–
z
z 1–
-----------
Tz
z 1–()
2
------------------
kT()
2
T
2
zz 1+()
z 1–()
3
-------------------------
ω
kTsin
z
ω
Tsin
z
2
2z
ω
T 1+cos–
---------------------------------------------
ω
Tcos
zz
ω
Tcos–( )
z
2
2z
ω
T 1+cos–
---------------------------------------------
e
akT–
z
ze
aT–
–
-----------------
kTe
akT–
zTe
aT–
ze
a– T
–()
2
------------------------
kT()
2
e
akT–
T
2
e
aT–
zz e
aT–
+()
ze
aT–
–()
3
----------------------------------------
e
akT–
ω
kTsin
ze
aT–
ω
Tsin
z
2
2ze
aT–
ω
Te
2aT–
+cos–
-------------------------------------------------------------
e
akT–
ω
cos kT
zz e–
aT–
ω
cos T( )
z
2
2ze
aT–
ω
Te
2aT–
+cos–
------------------------------------------------------------
a
k
ω
sin kT
az
ω
sin T
z
2
2az
ω
Ta
2
+cos–
-------------------------------------------------
a
k
ω
cos kT
zz a–
ω
cos T( )
z
2
2az
ω
Ta
2
+cos–
-------------------------------------------------

© 2003 by CRC Press LLC
Fourier Series
The periodic function f (t) with period 2π may be represented by the trigonometric series
where the coefficients are determined from
Such a trigonometric series is called the Fourier series corresponding to f (t) and the coefficients are
termed Fourier coefficients of
f (t). If the function is piecewise continuous in the interval – π ≤ t ≤ π and
has left- and right-hand derivatives at each point in that interval, then the series is convergent with sum
f (t) except at points t
i
, at which f (t) is discontinuous. At such points of discontinuity, the sum of the
series is the arithmetic mean of the right- and left-hand limits of
f (t) at t
i
. The integrals in the formulas
for the Fourier coefficients can have limits of integration that span a length of 2
π, for example, 0 to 2π
(because of the periodicity of the integrands).
Functions with Period Other Than 2π
If f (t) has period P, the Fourier series is
where
Again, the interval of integration in these formulas may be replaced by an interval of length P, for
example, 0 to
P.
Bessel Functions
Bessel functions, also called cylindrical functions, arise in many physical problems as solutions of the
differential equation
a
0
a
n
nt b
n
ntsin+cos( )
1
∞
∑
+
a
0
1
2
π
------
ft() td
π
–
π
∫
=
a
n
1
π
---
ft() nt tdcos
π
–
π
∫
=
b
n
1
π
---
ft() nsin tt d
π
–
π
∫
n 1, 2, 3,K=( )=
ft() a
0
a
n
2
π
n
P
----------
tb
n
2
π
n
P
----------
tsin+cos
1
∞
∑
+
∼
a
0
1
P
---
ft() td
P 2⁄–
P 2⁄
∫
=
a
n
2
P
---
ft()
2
π
n
P
----------
cos ttd
P 2
⁄
–
P 2
⁄
∫
=
b
n
2
P
---
ft()
2
π
n
P
----------
sin ttd
P 2
⁄
–
P 2
⁄
∫
=
x
2
y″ xy′ x
2
n
2
–()y++ 0=
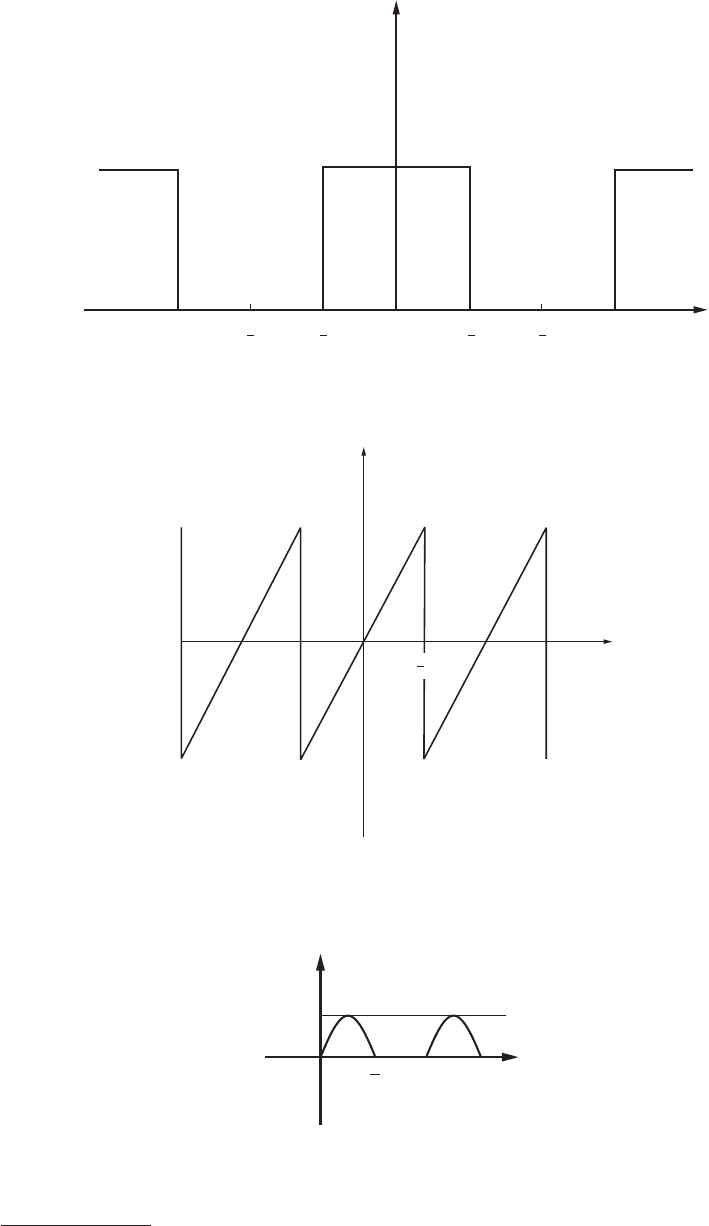
© 2003 by CRC Press LLC
FIGURE 36 Square wave.
FIGURE 37 Sawtooth wave. .
FIGURE 38 Half-wave rectifier.
f(t)
a
t
−
1
2
P
−
1
4
P
1
4
P
1
2
P
0
ft()
a
2
---
2a
π
------
2
π
t
P
---------
1
3
---
6
π
t
P
---------
1
3
---
10
π
t
P
------------ L +cos+cos–cos
.+∼
f (t)
a
o
t
P
1
2
f
t()
2a
π
------
2
π
t
P
---------
1
2
---
4
π
t
P
---------
1
3
---
6
π
t
P
---------
L –sin+sin–sin
∼
f (t)
A
O
t
π
ω
ft()
A
π
---
A
2
---
ω
t
2A
π
-------
1
1()3()
----------------
2
ω
t
1
3()5()
----------------
4
ω
t L +cos+cos
.–sin+∼

© 2003 by CRC Press LLC
which is known as Bessel’s equation. Certain solutions of the above, known as Bessel functions of the first
kind of order n,
are given by
In the above it is noteworthy that the gamma function must be defined for the negative argument q:
Γ(q) = Γ(q + 1)/q, provided that q is not a negative integer. When q is a negative integer, 1/Γ(q) is
defined to be zero. The functions
J
–n
(x) and J
n
(x) are solutions of Bessel’s equation for all real n. It is
seen, for
n = 1, 2, 3, K, that
and, therefore, these are not independent; hence, a linear combination of these is not a general solution.
When, however,
n is not a positive integer, a negative integer, or zero, the linear combination with arbitrary
constants
c
1
and c
2
is the general solution of the Bessel differential equation.
The zero-order function is especially important as it arises in the solution of the heat equation (for a
“long” cylinder):
while the following relations show a connection to the trigonometric functions:
The following recursion formula gives J
n + 1
(x) for any order in terms of lower-order functions:
Legendre Polynomials
If Laplace’s equation, ∇
2
V = 0, is expressed in spherical coordinates, it is
and any of its solutions, V (r,
θ
,
φ
), are known as spherical harmonics. The solution as a product
J
n
x()
1–()
k
k!Γ nk1++()
-----------------------------------
x
2
--
n 2k+
k 0=
∞
∑
=
J
n–
x()
1–()
k
k!Γ n– k 1++( )
----------------------------------------
x
2
--
n– 2k+
k 0=
∞
∑
=
J
n–
x() 1–()
n
J
n
x()=
yc
1
J
n
x() c
2
J
n–
x()+=
J
0
x() 1
x
2
2
2
----–
x
4
2
2
4
2
----------
x
6
2
2
4
2
6
2
---------------– L+ +=
J
1
2
--
x()
2
π
x
------
12⁄
xsin=
J
1
2
--–
x()
2
π
x
------
12⁄
xcos=
2n
x
------
J
n
x() J
n 1–
x() J
n 1+
x()+=
r
2
θ
δ
2
V
δ
r
2
---------
sin 2r
θ
δ
V
δ
r
-------
sin
θ
δ
2
V
δθ
2
---------
sin
θ
cos
δ
V
δθ
-------
1
θ
sin
-----------
δ
2
V
δφ
2
---------
+ + ++ 0=

© 2003 by CRC Press LLC
which is independent of
φ
, leads to
Rearrangement and substitution of x = cos
θ
leads to
known as Legendre’s equation. Important special cases are those in which n is zero or a positive integer,
and, for such cases, Legendre’s equation is satisfied by polynomials called Legendre polynomials,
P
n
(x).
A short list of Legendre polynomials, expressed in terms of
x and cos
θ
, is given below. These are given
by the following general formula:
where L = n/2 if n is even and L = (n – 1)/2 if n is odd.
Additional Legendre polynomials may be determined from the recursion formula
or the Rodrigues formula
Vr
θφ
,,()Rr()Θ
θ
()=
θ
2
sin Θ″
θθ
Θ′cossin nn 1+()
θ
2
sin[ ]Θ+ + 0=
1 x
2
–()
x
2
2
d
d Θ
2x
xd
dΘ
– nn 1+()Θ+ 0=
P
n
x()
1–()
j
2n 2j–()!
2
n
j! nj–()! n 2j–()!
-----------------------------------------------
x
n 2j–
j 0=
L
∑
=
P
0
x() 1=
P
1
x() x=
P
2
x()
1
2
--
3x
2
1–()=
P
3
x()
1
2
--
5x
3
3x–()=
P
4
x()
1
8
--
35x
4
30x
2
– 3+( )=
P
5
x()
1
8
--
63x
5
70x
3
– 15x+( )=
P
0
θ
cos()1=
P
1
θ
cos()
θ
cos=
P
2
θ
cos()
1
4
--
32
θ
1+cos( )=
P
3
θ
cos()
1
8
--
53
θ
3
θ
cos+cos( )=
P
4
θ
cos()
1
64
-----
35 4
θ
20 2
θ
9+cos+cos( )=
n 1+()P
n 1+
x() 2n 1+()xP
n
x() nP
n 1–
x()+– 0 (n 1, 2, K )= =
P
n
x()
1
2
n
n!
----------
d
n
dx
n
--------
x
2
1–()
n
=

© 2003 by CRC Press LLC
Laguerre Polynomials
Laguerre polynomials, denoted L
n
(x), are solutions of the differential equation
and are given by
Thus,
Additional Laguerre polynomials may be obtained from the recursion formula
Hermite Polynomials
The Hermite polynomials, denoted H
n
(x), are given by
and are solutions of the differential equation
The first few Hermite polynomials are
Additional Hermite polynomials may be obtained from the relation
where prime denotes differentiation with respect to x.
Orthogonality
A set of functions { f
n
(x)} (n = 1, 2, K ) is orthogonal in an interval (a, b) with respect to a given weight
function
w(x) if
xy ″ 1 x–()y′ ny++0=
L
n
x()
1–()
j
j!
------------
j 0=
n
∑
C
nj,()
x
j
(n 0, 1, 2, K )==
L
0
x() 1=
L
1
x() 1 x–=
L
2
x() 12x–
1
2
--
x
2
+=
L
3
x() 13x–
3
2
--
x
2
1
6
--
x
3
–+=
n 1+()L
n 1+
x() 2n 1 x–+( )L
n
x()– nL
n 1–
x()+ 0=
H
0
1= H
n
x(), 1–()
n
e
x
2
d
n
e
x
2
–
dx
n
-------------
(n 1, 2, K )==
y
″ 2xy′– 2ny+ 0 (n 0, 1, 2, K )==
H
0
1 H
1
x() 2x= =
H
2
x() 4x
2
2 H
3
x()– 8x
2
12x–= =
H
4
x() 16x
4
48x
2
– 12+=
H
n 1+
x() 2xH
n
x() H′
n
x()–=
wx()f
m
x()f
n
x()xd
a
b
∫
0 when mn≠=
© 2003 by CRC Press LLC
The following polynomials are orthogonal on the given interval for the given w(x):
The Bessel functions of order n, J
n
(λ
1
x), J
n
(λ
2
x), K, are orthogonal with respect to w(x) = x over the
interval (0,
c), provided that the λ
i
are the positive roots of J
n
(λc) = 0:
where n is fixed and n ≥ 0.
Statistics
Arithmetic Mean
where X
i
is a measurement in the population and N is the total number of X
i
in the population. For a
sample of size n, the sample mean, denoted , is
Median
The median is the middle measurement when an odd number (n) of measurements is arranged in order;
if
n is even, it is the midpoint between the two middle measurements.
Mode
The mode is the most frequently occurring measurement in a set.
Geometric Mean
Harmonic Mean
The harmonic mean H of n numbers X
1
, X
2
, K, X
n
is
Legendre polynomials:
Laguerre polynomials:
Hermite polynomials
P
n
x()
wx() 1=
a 1, b– 1==
L
n
x()
wx() x–()exp=
a 0, b ∞==
H
n
x()
wx() x
2
–()exp=
a ∞– b,∞==
xJ
n
λ
j
x()J
n
λ
k
x()xd
0
c
∫
0 jk≠()=
µ
ΣX
i
N
--------=
X
X
ΣX
i
n
--------=
geometric mean X
1
X
2
KX
n
n
=
H
n
Σ 1 Xi()⁄()
--------------------------=
© 2003 by CRC Press LLC
Variance
The mean of the sum of squares of deviations from the mean (µ) is the population variance, denoted σ
2
:
The sample variance, s
2
, for sample size n is
A simpler computational form is
Standard Deviation
The positive square root of the population variance is the standard deviation. For a population,
for a sample
Coefficient of Variation
Probability
For the sample space U, with subsets A of U (called “events”), we consider the probability measure of an
event
A to be a real-valued function p defined over all subsets of U such that:
If A
1
and A
2
are subsets of U, then
Two events A
1
and A
2
are called mutually exclusive if and only if (null set). These events
are said to be independent if and only if
σ
2
Σ X
i
µ
–()
2
N⁄=
s
2
Σ X
i
X–()
2
n 1–()⁄=
s
2
ΣX
i
2
ΣX
i
()
2
n
---------------–
n 1–
-------------------------------=
σ
ΣX
i
2
ΣX
i
()
2
N
---------------–
N
-------------------------------
12⁄
=
s
ΣX
i
2
ΣX
i
()
2
n
---------------–
n 1–
-------------------------------
12⁄
=
VsX⁄=
0 pA() 1≤≤
pU() 1 and p Φ() 0= =
pA
1
A
2
∪()pA
1
()pA
2
()pA
1
A
2
∩()–+=
A
1
A
2
∩
φ
=
pA
1
A
2
∩()pA
1
()pA
2
().=

© 2003 by CRC Press LLC
Conditional Probability and Bayes’ Rule
The probability of an event A, given that an event B has occurred, is called the conditional probability
and is denoted
p(A/B). Further,
Bayes’ rule permits a calculation of a posteriori probability from given a priori probabilities and is
stated below:
If A
1
, A
2
, K, A
n
are n mutually exclusive events, and p(A
1
) + p(A
2
) + K + p(A
n
) = 1, and B is any
event such that
p(B) is not 0, then the conditional probability p(A
i
/B) for any one of the events A
i
, given
that B has occurred
, is
Example
Among five different laboratory tests for detecting a certain disease, one is effective with probability 0.75,
whereas each of the others is effective with probability 0.40. A medical student, unfamiliar with the
advantage of the best test, selects one of them and is successful in detecting the disease in a patient. What
is the probability that the most effective test was used?
Let B denote (the event) of detecting the disease, A
1
the selection of the best test, and A
2
the selection
of one of the other four tests; thus,
p(A
1
) = 1/5, p(A
2
) = 4/5, p(B/A
1
) = 0.75, and p(B/A
2
) = 0.40. Therefore,
Note that the a priori probability is 0.20; the outcome raises this probability to 0.319.
Binomial Distribution
In an experiment consisting of n independent trials in which an event has probability p in a single trial,
the probability
P
X
of obtaining X successes is given by
where
The probability of between a and b successes (both a and b included) is P
a
+ P
a + 1
+ L + P
b
, so if a =
0 and
b = n, this sum is
Mean of Binomially Distributed Variable
The mean number of successes in n independent trials is m = np, with standard deviation
pA B⁄()
pA B∩()
pB()
----------------------=
p
A
i
B⁄()
PA
i
()pB A
i
⁄()
pA
1
()pB A
1
⁄()pA
2
()pB A
2
⁄()L pA
n
()pB A
n
⁄()+ ++
-------------------------------------------------------------------------------------------------------------------------------------=
p
A
1
B⁄()
1
5
--
0.75()
1
5
--
0.75()
4
5
--
0.40()+
------------------------------------------- 0.319= =
P
X
C
nX,()
p
X
q
nX–()
=
q 1 p–() and C
nX,()
n!
X! nX–()!
-------------------------= =
C
nX,()
p
X
q
nX–()
X 0=
n
∑
q
n
C
n 1,()
q
n 1–
pC
n 2,()
q
n 2–
p
2
L p
n
+ + ++ qp+()
n
1= = =
σ
npq.=
