Волков В.Л. Моделирование процессов и систем
Подождите немного. Документ загружается.

Н.Новгород. 1997
В.Л. Волков
МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ
И СИСТЕМ
ДИНАМИЧЕСКАЯ
СИСТЕМА
ДАТЧИКИ
ИНФОРМАЦИОННЫЕ
ПРОЦЕССЫ
U Y
X
X V
V
1
Министерство образования Российской федерации
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ И СИСТЕМ
Учебное пособие
Н. Новгород. 1997
2
УДК: 681.5.01:621.317.08 (075.8)
Моделирование процессов и систем: Учеб.пособие /В.Л.Волков;
Нижегород. гос. техн. ун-т. Н.Новгород, 2005. 80 с. ISBN 5-230-03038-0.
Описываются математические модели динамических систем и
информационных процессов, вероятностные модели случайных процессов,
математические модели физических процессов. Рассматриваются методы
вычислительных экспериментов по моделированию и исследованию
процессов и систем на ПЭВМ.
Предназначено для студентов технических специальностей.
Рис.26. Табл.3. Библиогр.: 30 назв.
Рецензенты: кафедра "Математического анализа и информатики"
Арзамасского государственного педагогического института;
канд. техн. наук В.В.Лосев
2304000000 - 005
К ———————— Тем. пл. - 1997 ББК 32.81
7К3(03) -97
ISBN 5-230-03038-0 © Волков В.Л., 1997
3
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 5
1. ПРОЦЕССЫ И ИХ СВОЙСТВА 6
1.1. Представление процессов через базисные функции 9
1.2. Теорема проецирования 10
1.3. Построение ортонормированного базиса 11
1.4. Импульсная теорема (теорема Котельникова) 12
2. СЛУЧАЙНЫЕ ПРОЦЕССЫ 14
2.1. Характеристики случайных процессов 15
2.2. Прохождение процесса через линейную динамическую систему 18
2.3. Расчет числовых характеристик случайных процессов 18
3. МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ И ПРОЦЕССОВ 19
3.1. Модели динамических систем и процессов 19
3.1.1. Модели информационных процессов 22
3.2. Методы формирования матричных моделей 23
3.2.1. Метод вспомогательной переменной 24
3.2.2. Метод последовательного интегрирования 27
3.2.3. Метод нормальной матричной формы Коши 28
3.2.4. Метод представления передаточной функции суммой дробей 30
3.2.5. Метод представления передаточной функции произведением дробей 32
3.3. Статистическое моделирование систем 34
3.3.1. Статистические испытания системы массового обслуживания 35
3.3.2. Математическое обеспечение статистических испытаний 39
3.3.3. Моделирование процессов с заданным законом распределения 40
3.3.2.2. Программа для испытаний систем массового обслуживания 42
3.3.2.3. Программа статистических испытаний надежности систем 44
3.4. Примеры формирования моделей процессов и систем 45
3.4.1. Моделирование датчиков при входном сигнале и аддитивном шуме 45
3.4.2. Моделирование процессов с заданными свойствами. 50
3.4.3. Моделирование системы по сигналу и возмущению 53
3.4.4. Моделирование системы при векторных измерениях 53
3.4.5. Моделирование комплексной измерительной системы 54
3.4.6. Моделирование импульсного радиодальномера 59
3.4.7. Моделирование движения летательного аппарата по тангажу 60
4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МОДЕЛИРОВАНИЯ 62
4.1. Пакет программ моделирования процессов и систем 62
4.4.1. Задачи моделирования 63
4.4.2. Интерактивный режим работы пакета программ 66
4.1.2.1. Горизонтальное меню 66
4.1.2.2. Диалоговое окно элементарных моделей 69
ПРИЛОЖЕНИЕ 1 70
ПРИЛОЖЕНИЕ 2 73
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 78
4
ВВЕДЕНИЕ
Развитие моделирования процессов и систем связано с необходимостью
их описания математическими моделями с последующим исследованием
путем вычислительного эксперимента на современных персональных ЭВМ.
При этом затрачивается неизмеримо меньше средств и времени на
проектирование перспективных систем, а часто без моделирования просто
невозможно проводить исследования, осуществлять прогнозирование или
выбирать оптимальные варианты систем. Моделирование - один из
перспективных способов изучения различных процессов и систем.
Задачи моделирования процессов и систем многообразны. Главные
направления моделирования: − имитационное, математическое, физическое и
статистическое. Основные задачи моделирования: − моделирование систем
массового обслуживания, моделирование кибернетических систем,
распознавание образов.
При физическом моделировании модель воспроизводит изучаемый
процесс (систему) с сохранением его физической природы (продувка моделей
в аэродинамических трубах и др.) [1]. При математическом моделировании
исследование различных явлений осуществляется при использовании
математических зависимостей на каком-либо формальном языке (выявляются
закономерности, строятся графики движения процессов и систем во времени
и т.д.). Математическое моделирование особенно эффективно при
исследовании проектируемых систем и при прогнозировании различных
явлений и процессов (например, при метеопрогнозах, при исследовании
ядерных реакций). При имитационном моделировании (стендовые
испытания) имитируются условия различных реальных режимов работы
системы и требуемые воздействия сигналов. При статистическом
моделировании к условиям моделирования добавляются случайные
изменения параметров системы, возмущения и шумы измерений физических
величин.
Наибольший интерес представляет моделирование кибернетических
систем с учетом протекающих в них процессов в различных режимах работы.
Техническая кибернетика [2] исследует системы автоматического управления
и информационно-измерительные системы. Кибернетика как наука об
управлении, получении, передаче и преобразовании информации использует
для описания процессов и систем дифференциальные уравнения и линейные
матричные преобразования.
5
Развитие современных методов моделирования создало предпосылки для
создания и исследования высокоэффективных кибернетических систем,
которые, как правило, ориентированы на цифровые алгоритмы обработки
информации, с применением современных бортовых цифровых
вычислительных машин, микропроцессоров и микро-ЭВМ.
1. ПРОЦЕССЫ И ИХ СВОЙСТВА
Теория процессов (сигналов) рассмотрена в ряде работ [2-7]. Здесь
приводятся основные понятия и положения теории процессов для
практических приложений, связанных с моделированием.
Процесс - это некоторая совокупность изменяющихся во времени
функций, имеющих одни и те же свойства (например, детерминированные -
неслучайные процессы, стохастические - случайные процессы). Большую
группу процессов составляют абсолютно интегрируемые, для которых
выполняется условие
Xtdt()
0
∞
∫
〈∞
. Имеется также группа физически
реализуемых процессов. К ним относятся процессы с ограниченной энергией.
Для них
X tdt
2
0
()
∞
∫
〈∞
. Эти процессы обозначаются L
2
(t). Основные задачи
изучения процессов - установление меры различения процессов и выявление
способов их преобразования.
Пространством процессов называется множество процессов,
обладающих каким-либо одним свойством, дополненное условием
различения процессов [2]. Мерой различения процессов служит расстояние.
Различение процессов осуществляется на числовой оси, на которую
отображаются процессы. Расстояние между процессами определяется
метрикой, обозначаемой d(X,Y)=d[X(t),Y(t)], где X(t), Y(t) - процессы.
Метрическим пространством называется множество, в котором задано
расстояние между каждыми двумя элементами в виде действительной
функции d(X,Y), удовлетворяющей трем аксиомам [2]:
1) d(X,Y)=d(Y,X); 2) d(X,Y)≥0; 3) d(X,Y)+d(Y,Z)≥d(X,Z). (1.1)
Понятие метрики определяется ее свойствами. Приведем примеры функций
от X, Y, которые могут быть взяты в качестве метрик [2]:
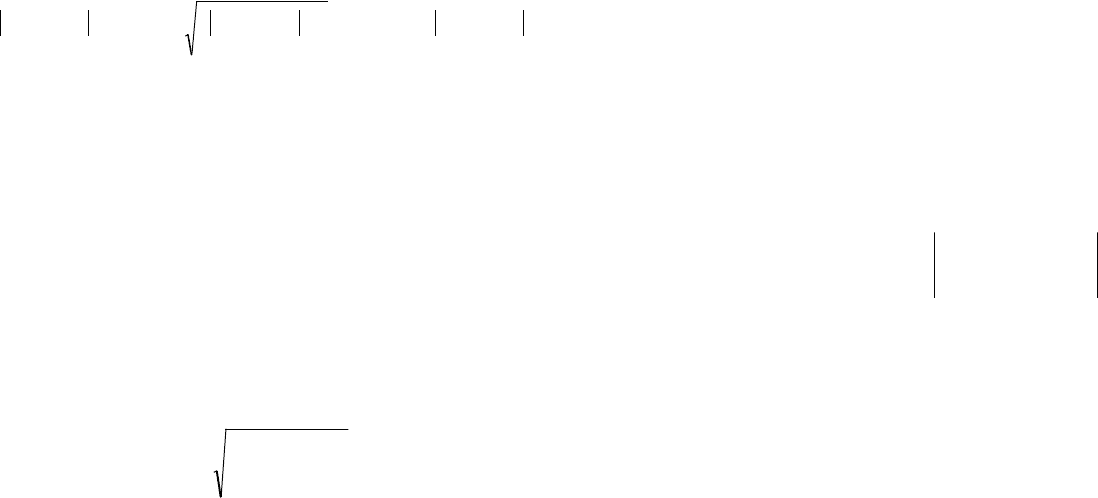
6
1 2
1 2
2
3
) () () ; ) () () sup () (). ; 3) d Xt Ytdt d Xt Yt dt d Xt Yt
t t
= − = − = −
∫ ∫
На практике наиболее часто применяется метрика d
2
.
Пространством состояний называется метрическое пространство,
каждый элемент которого полностью определяет состояние рассматриваемой
системы (процесса) [5].
Каждая система, рассматриваемая в пространстве состояний, разделяется
на взаимосвязанные подсистемы (субсистемы). Пространство состояний в
этом случае представляется совокупностью субпространств состояний
(сечений пространства). Элементами пространства состояний являются
конечномерные совокупности действительных чисел - векторы состояния
X=[x
1
,...,x
n
]
т
[5]. Примеры: X(t)=[x
1
(t),...,x
n
(t)]
т
; X(k)=[x
1
(k),...,x
n
(k)]
т
, где т - знак
транспонирования.
Элементами евклидова пространства состояний являются векторы
X=[x
1
,...,x
n
]
т
, для которых расстояние выражается формулой [5]
dXX x x
j j
j
n
(', ") (' ").= −
=
∑
2
1
Линейное пространство. Кроме различения процессов необходимо иметь
возможность производить над ними некоторые действия. Рассмотрим в
качестве действий над процессами линейные преобразования X+Y, aX, где X,
Y - процессы; a -скалярный коэффициент. Действия над процессами
удовлетворяют основным свойствам линейной алгебры:
1) коммутативное свойство: X+Y=Y+X;
2) ассоциативное свойство: (X+Y)+Z=X+(Y+Z);
3) если X+Y=X, то Y=0 (Y - нулевой вектор);
4) a(X+Y)=aX+aY (a - скалярный коэффициент);
5) abX=b(aX) (a, b - скалярные коэффициенты);
6) (a+b)X=aX+bX.
Пространство процессов, где возможны линейные преобразования
процессов в соответствии с правилами линейной алгебры, называется
линейным пространством (ЛП) [2].
Базисом векторов X
1
,...,X
n
называется линейно независимая подсистема,
через которую выражаются все X
1
,...,X
n
[3]. Из линейной алгебры также
7
известно определение линейной комбинации векторов
aX
j j
j
n
=
∑
1
, где a
j
-
скалярные коэффициенты. Условие линейной независимости векторов
выражается через линейную комбинацию
aX
j j
j
n
=
=
∑
0
1
только при a
j
=0.
Условие линейной независимости X
j
определяется и через определитель
Грамма (D):
D
X X X X
X X X X
n
n n n
= ≠
( , )...( , )
...
( , )...( , )
,
1 1 1
1
0
где (X
i
,X
j
) - скалярное произведение векторов.
Скалярным произведением процессов X
i
(t), X
j
(t) является выражение
( , ) () ()
*
X X XtX tdt
i j i j
=
∞
∫
0
, (1.2)
где X
j
*
- комплексно-сопряженный вектор.
Свойства скалярного произведения:
1) (aX+bY,Z)=a(X,Z)+b(Y,Z); 2) (X,X)≥0; 3) (X,Y)=(Y,X)*, (1.3)
откуда могут быть получены следствия (aX,Y)=a(X,Y), (X,aY)=a*(X,Y).
Скалярное произведение (X,Y) (1.2) при дискретных процессах
X(k)=[x(1),...,x(n)]
т
, Y(k)=[y(1),...,y(n)]
т
вычисляется через сумму
( ,) ()()XY xkyk
k
n
=
=
∑
1
или в матричном виде (X,Y)=X
т
(k)Y(k).
Норма процесса Х(t) определяется соотношением
||Х||=(Х,Х)
1/2
. (1.4)
Существуют три основных свойства нормы [2]:
1) ||X||≥0;
2) ||X+Y||≤||X||+||Y||; (1.5)
3) ||aX||=|a| ||X||.
Докажем их на основе свойств скалярного произведения (1.3). Первое
свойство вытекает из условия (X,X)
0,5
≥0. Для доказательства второго свойства
требуется неравенство Шварца (Коши−Буняковского) |(X,Y)|
2
≤(X,X)
(Y,Y). Используем квадрат нормы ||X+Y||
2
=(X+Y,X+Y)=(X,X)+
8
+(X,Y)+(Y,X)+(Y,Y) и неравенство Шварца, заменим (X,Y) и (Y,X) в
соответствии с неравенством Шварца и получим ||X+Y||
2
≤(X,X)+
+2[(X,X)(Y,Y)]
1/2
+(Y,Y). Учитывая, что в правой части неравенства имеется
полный квадрат слагаемых (X,X) и (Y,Y), запишем ||X+Y||
2
≤[(X,X)
1/2
+(Y,Y)
1/2
]
2
или после извлечения квадратного корня из обеих частей ||X+Y||≤||X||+||Y||.
Для доказательства третьего свойства рассмотрим процесс Z=aX. Для него
запишем выражение (Z,Z)=(aX,aX)=a(X,aX)=a(aX,X)'=aa'(X,X)'=|a|
2
(X,X).
Поскольку ||Z||=(Z,Z)
1/2
, получим ||aX||=|a| ||X||.
Связь метрического и линейного пространств. Свойство метризуемости
ЛП следует из того, что норма разности двух процессов обладает свойствами
метрики, т.е. является метрикой ||X-Y||=d
2
(X,Y). Докажем это утверждение
путем проверки свойств метрики (1.1). Первое свойство метри-ки
d
2
(X,Y)=d
2
(Y,X) выполняется, так как ||X-Y||=||-(Y-X)=|-1|||Y-X||=
=||Y-X||. Второе свойство выполняется, поскольку норма ||X-Y||≥0 (1.5). Для
доказательства третьего свойства d
2
(X,Y)+d
2
(Y,Z)≥d
2
(X,Z) запишем норму
разности ||X-Y||+||Y-Z||≥||X-Z||. Учтем ||X-Z||=||(X-Y)+(Y-Z)|| и используем
второе свойство нормы ||(X-Y)+(Y-Z)||≤||X-Y||+||Y-Z||. Свойства метрики для
||X-Y|| выполняются, и поэтому ЛП является метрическим.
Ортогональными называются процессы, скалярное произведение которых
равно нулю [2]: (f
i
,f
j
)=0. Для ортонормированных процессов, кроме того, (f
i
,
f
i
)=1. Матричная форма записи ортонормированного базиса
F
т
F=I, (1.6)
где F=[f
1
(t),..., f
n
(t)]; I - единичная матрица.
Задача. Показать, что ортонормированная система функций является
базисом процессов. Базис предполагает линейную независимость подсистемы
функций F=(f
1
,...,f
n
), а условие линейной независимости векторов в линейной
алгебре определяется через определитель Грамма (D≠0). Определитель
D=|F
т
F| в данном случае равен 1, т.е. не равен нулю, так как для
ортонормированной системы функций выполняется (1.6).
1.1. Представление процессов через базисные функции
Сигнал X(t) представим через базисные функции F
Xt aft
ii
i
n
() ()=
=
∑
1
, (1.7)
где a
i
- скалярные коэффициенты, или в матричной форме
9
X=FA, (1.8)
где F=[f
1
(t),...,f
n
(t)]; A=(а
1
,...,а
n
)
т
. Коэффициенты a
i
можно найти в
компактной матричной форме. В случае, если базис F является
ортонормированным, коэффициенты определяются из (1.8). Умножим
последнее соотношение на F
т
слева: F
т
X=F
т
FA. Учитывая (1.6), получим
A=F
т
X. Произведение F
т
X является вектором скалярных произведений
A
Xf
Xf
n
=
( , )
...
( , )
1
,
где коэффициенты a
j
рассчитываются по формуле
a Xtf tdt
j j
=
∞
∫
() ()
*
0
.
Если F
т
F≠ I, то для вычисления вектора A имеем формулу A=(F
т
F)
-1
F
т
X.
Обратная матрица (F
т
F)
-1
рассчитывается на основе матрицы Грамма:
( )
( , )...( , )
...
( , )...( , )
FF
f f f f
f f f f
n
n n n
т
=
1 1 1
1
.
Сигналы, принадлежащие пространству базисных функций (пространству
Mn), представляются в этом пространстве с абсолютной точностью. Но чаще
имеют место реальные сигналы, не принадлежащие пространству Mn. В этом
случае возможно приближенное представление сигналов путем их
проецирования в пространство Mn оптимальным образом.
1.2. Теорема проецирования
Для реального сигнала L
2
, не принадлежащего пространству базисных
функций Mn (X∉ Mn), существует его представление Х^(t), принадлежа-щее
Mn (Х^∈ Mn):
X t XVf
i i
i
n
^() ( , ) .=
=
∑
1
(1.9)
Здесь (X-X^)⊥ f
i
(ортогонально всем f
i
), а норма
||X-X^||≤||X-X′ ||, (1.10)
где X′∈ Mn; V - взаимный базис (V
т
F=I).
Доказательство. Рассмотрим (X-X^,V
i
), подставляя (1.9):

10
( ( , ) , ) ( , ) ( , )( , )X XV fV XV XV fV
k ki
k
n
i k ki
k
n
− = − =
= =
∑ ∑
1 1
= − = − =
=
∑
(,) (, ) (,)(,) ,XV XV XV XV
i k ki
k
n
i i
δ
1
0
где δ
ki
- символ Кроннекера. Получим (X-X^,Vi)=0, т.е. выполняется условие
ортогональности. Рассмотрим (X-X^,X′), представив X′ в виде (1.7)
X bV
ii
i
n
'=
=
∑
1
,
получим
( ^, ') ( ^, ) ( ^, )
*
X X X X X bV b X XV
ii
i
n
i i
i
n
− = − = − =
= =
∑ ∑
1 1
0
, т.е. (X-X^)
ортогонально любому Х′ пространства Mn. Теперь докажем положение (1.10)
теоремы. Для этого рассмотрим ||X-X′||
2
=||(X-X^)-(X′-
-X^)||
2
. Представим правую часть через скалярное произведение (1.4):
||(X-X^)-(X′-X^)||
2
=((X-X^)-(X′-X^),(X-X^)-(X′-X^))=
=(X-X^,X-X^)-(X-X^,X′-X^)-(X′-X^,X-X^)+(X′-X^,X′-X^).
Учитывая, что (X′-X^)∈ Mn, имеем (X-X^,X′-X^)=0, (X′-X^,X-
X^)=0. При этом получим ||X-X′||
2
=(X-X^,X-X^)+(X′-X^,X′-X^)=
=||X-X^||
2
+||X′-X^||
2
,
откуда следует, что минимум ||X-X′||
2
возможен только
при X′=X^. Таким образом, (1.10) доказано и доказана теорема.
1.3. Построение ортонормированного базиса
Построение ортонормированного базиса называют процедурой
Грамма−Шмидта. Пусть имеется произвольный (не ортогональный) базис
U=(u
1
,...,u
n
), необходимо построить ортонормированный F=(f
1
,..., f
n
) [3].
Первый шаг преобразования. Выразим f
1
=a
1
u
1
(геометрическая интерпретация представлена на
рис.1.1). Умножим обе части этого соотношения
скалярно на f
1
справа: (f
1
,f
1
)=a
1
(u
1
,f
1
), подставим в
правой части f
1
=a
1
u
1
и (f
1
,f
1
)=1, получим 1=a
1
(u
1
,a
1
u
1
).
Вынося a
1
за знак скалярного произведения и учитывая
выражение(u
1
,u
1
)=||u
1
||
2
, получим |a
1
|
2
||u
1
||
2
=1, откуда имеем коэффициент
f
1
u
1
Рис.1.1
11
a
1
=1/||u
1
||. Таким образом, первая компонента вектора F представляется в
виде f
1
=u
1
/||u
1
||.
Второй шаг преобразования. Выразим f
2
через (u
2
-u
2
^), считая u
2
^
проекцией сигнала u
2
в пространство, образованное на базисных функциях F:
f
2
=(u
2
-u
2
^)a
2
. С учетом ортонормирования (f
2
,f
2
)=1, (f
1
,f
2
)=0 и того, что на
основании теоремы проецирования (u
2
-u
2
^,f
1
)=0, где u
2
^=b
1
f
1
, b
1
=(u
2
,f
1
), а
следовательно, (f
2
,f
2
-u
2
^)=
=a
2
(u
2
-u
2
^,f
2
-u
2
^)=1, получим
второй коэффициент a
2
=1/||u
2
-
u
2
^||. Таким образом, вторая
компонента вектора F имеет вид
f
2
=(u
2
-u
2
^)/||u
2
-u
2
^||.
Геометрическая интерпретация
для двухмерного случая представлена на рис.1.2.
Третий шаг преобразования. Выразим f
3
через (u
3
-u
3
^), считая u
3
^
проекцией сигнала u
3
в пространство, образованное на базисных функциях F,
причем f
3
=(u
3
-u
3
^)a
3
. С учетом ортонормирования (f
3
,f
3
)=1, (f
i
,f
j
)=0 и того, что
на основании теоремы проецирования (u
3
-u
3
^,f
1
)=0, где u
3
^=b
1
f
1
+b
2
f
2
,
bi=(u
3
,fi), а следовательно, (f
3
,f
3
-
u
3
^)=a
3
(u
3
-u
3
^,f
3
-
-u
3
^)=1, получим третий
коэффициент a
3
=1/||u
3
-u
3
^||.
Третья компонента вектора F
имеет вид f
3
=(u
3
-u
3
^)/||u
3
-u
3
^||. Геометрическая интерпретация для
трехмерного случая представлена на рис.1.3.
N-й шаг преобразования. Выразим f
n
через (u
n
-u
n
^), считая u
n
^ проекцией
сигнала u
n
в пространство базисных функций F. По аналогии N-я компонента
вектора F имеет вид f
n
=(u
n
-u
n
^)/||u
n
-u
n
^||.
Практическая ценность процедуры Грамма−Шмидта состоит в получении
ортонормированного базиса из произвольного, что позволяет легко находить
коэффициенты для оптимальной оценки сигнала:
a Xtf tdt
j j
=
∞
∫
() () .
*
0
Рис.1.2
f1
f
2
u2 u2
-
u2
^
u
2
^
f1
f
2
u
3
u3
-
u3
^
u2
^
f3
Рис.1.3
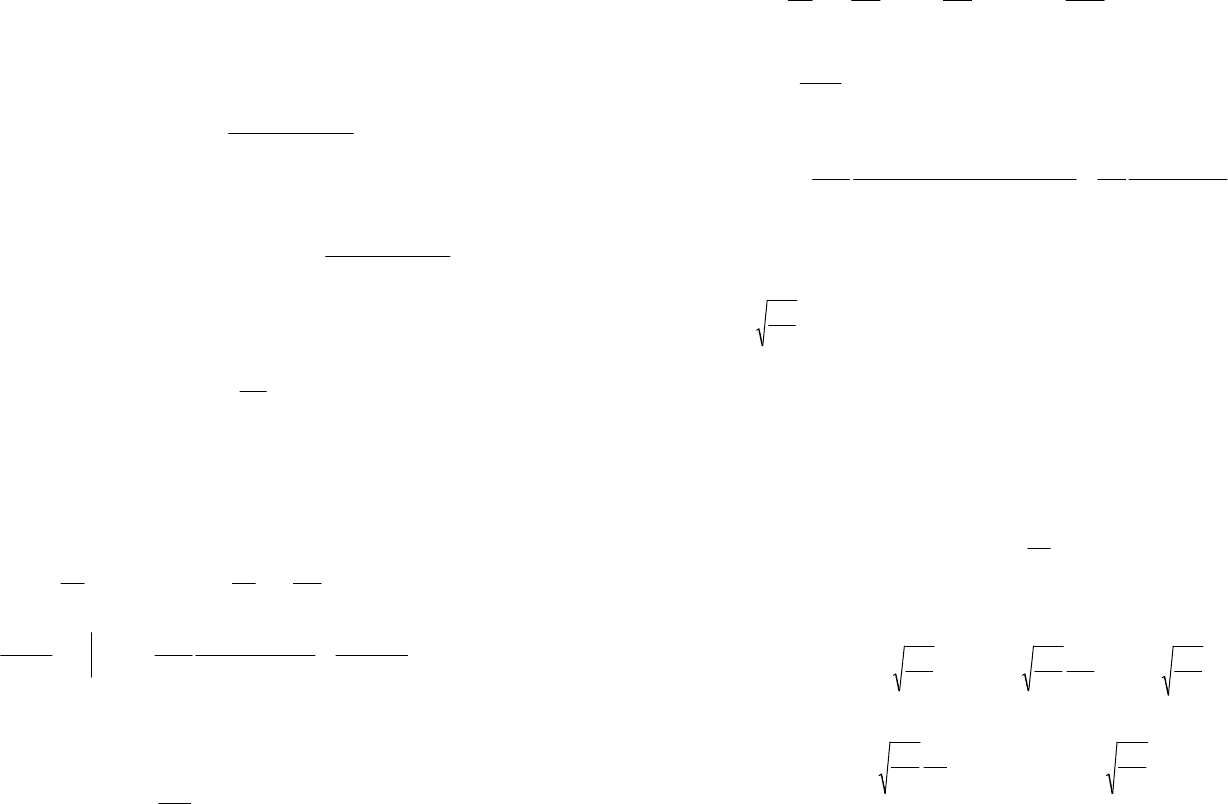
12
1.4. Импульсная теорема (теорема Котельникова)
Если наивысшая частота в спектре процесса Х(t) не больше F
m
, то
функция X(t) полностью определяется последовательностью своих
дискретных значений в моменты, отстоящие друг от друга не более чем на
1/(2F
m
) с [4]:
Xt XkT
w t kT
w t kT
m
m
() ( )
sin[ ( )]
( )
,=
−
−
−∞
∞
∑
(1.11)
где T - период дискретизации (T=1/(2F
m
)=π/w
m
); w
m
- предельная круговая
частота процесса X(t) (w
m
=2πF
m
); k - номер точки отсчета. Рассмотрим
свойства функций отсчета U=(u
0,
...,u
n
), где
ut
wt kT
w t kT
k
m
m
()
sin[ ( )]
( )
=
−
−
. Прежде
всего покажем ортогональность функций отсчета: (u
k
,u
s
)=0, (u
k
,u
k
)≠0.
Выражение для скалярного произведения будем искать в виде
( , ) () () ( ) ( )
*
u u u tu tdt u jwu jwdw
k s k s
t
k s
= = −
∫ ∫
−∞
∞
1
2π
(1.12)
на основании теоремы свертки для спектров. Определим спектральные
функции u
k
(jw), u
s
(-jw). Сначала найдем спектр функции u
0
(t). Известно, что
он постоянен в диапазоне [-w
m
,w
m
] и равен нулю за пределами (u
0
(jw)=π/w
m
при w∈[-w
m
,w
m
]
и u
0
(jw)=0 при w∉[-w
m
,w
m
]). Запишем
u t u jwe dw
w
e dw
jwt
m
jwt
wm
wm
0 0
1
2
1
2
() ( )= = =
−∞
∞
−
∫ ∫
π π
π
=
−
=
−
=
−
1
2
1
2jtw
e
w
w
w
e e
jt
wt
wt
m
jwt
m
m
m
jwt jwt
m
m
m m
sin( )
.
Для u
k
(t) спектр определяется на основании u
0
(jw) при использовании
свойства преобразования Фурье (теоремы сдвига сигналов). В соответствии с
этим свойством, если u
k
(t)=u
0
(t-kT), то u
k
(jw)=u
0
(jw)e
-jwkт
. Для спектра
процесса u
k
(t) получим
u jw
w
e
k
m
jwkT
( ) =
−
π
при w∈[-w
m
,w
m
]
и u
k
(jw)=0 при
w∉ [-w
m
,w
m
].
Вернемся к доказательству ортогональности функций отсчета, для этого
подставим в (1.12) найденные выражения спектров u
k
(jw), u
s
(-jw):
13
( , )
( )
u u
w
e
w
e dw
w
e dw
k s
m
jwsT
wm
wm
m
jwkT
m
jwksT
wm
wm
= = =
−
−
− −
−
∫ ∫
1
2
2
2
π
π π π
[ ]
= − + −
−
∫
π
2
2
w
wTk s j wTk sdw
m
wm
wm
cos( ( ) sin( ( )
.
Поскольку интеграл от второго слагаемого равен нулю, то имеем
( , )
sin[( )] sin[ ( )]
( )
sin[( )]
( )
.u u
w
k s k s
k s w
k s
k s
k s
m m
=
−
−
−
−
−
=
−
−
π
π
π
π
π
π
π2
Теперь докажем непосредственно импульсную теорему. Определим
представление X(t) в общем виде в конечномерном пространстве Mn,
образованном на базисных функциях F, которые выражаются через u
k
(t) в
виде
f t
w
u t
k
m
k
() ()=
π
(функции f
k
(t) составляют ортонормированный базис в
соответствии с их нахождением по процедуре Грамма−Шмидта).
Представление X(t) в базисе F имеет вид
Xt af
kk
k
n
()=
=
∑
0
, (1.13)
где a
k
=(X, f
k
). Найдем (X, f
k
) по свойству свертки преобразования Фурье:
( , ) () () ( ) ( )
*
Xf Xtf tdt Xjwf jwdw
k k k
= = −
−∞
∞
−∞
∞
∫ ∫
1
2π
. (1.14)
Спектр функции f
k
(t) в диапазоне [-w
m
,w
m
] получим на основе спектра
функции u
k
(t).
{ } { }
f jw Ff t
w
Fu t
w
w
e
w
e
k k
m
k
m
m
jwkT
m
jwkT
( ) () () .
* *
− = = = =
π π
π π
Подставим в (1.14) f
k
(-jw) и получим выражение для коэффициентов a
k
:
a Xf
w
Xjwe dw
w
XkT
k k
m
jwkT
Wm
Wm
m
= = =
−
∫
( , ) ( ) ( ).
π
π
π1
2
Подставим выражения f
k
(t) и a
k
в (1.13) и получим формулу дискретного
представления X(t) и доказательство теоремы, т.е. формулу (1.11).
Дискретные значения X(kT) обычно записываются в виде вектора
X
d
=[X(k),...,X(n)]
т
дискретных по времени значений. Матричная форма записи
X(t) в этом случае имеет стандартный вид X=FX
d
.

14
2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
Подробные сведения о случайных процессах широко представлены в
литературе, например [7], здесь приводятся только основные определения и
практические сведения, необходимые для моделирования. Известно, что
полезные сигналы и помехи в технических кибернетических системах
являются в общем случае случайными (стохастическими).
Случайным процессом (сигналом) называется функция времени, которая в
каждый момент времени является случайной величиной [7]. Для
проектирования точных информационно-измерительных систем необходимо
знать свойства полезных сигналов и помех. Случайный процесс определяется
функцией плотности распределения f(X,t), но исследование случайных
процессов с ее помощью - непростая задача, поэтому часто пользуются
статистическими характеристиками. К ним относятся: математическое
ожидание M(t), дисперсия Dx, корреляционная функция R(τ), спектральная
плотность S(w).
Гауссовским процессом является стохастический процесс, имеющий
гауссовский (нормальный) закон распределения. Белый шум - это случайный
процесс с равномерным распределением спектра мощности во всем диапазоне
частот (с постоянной интенсивностью).
Дискретное представление процесса в ортонормированном базисе
комплексных функций гармонического ряда Фурье определяется формулой
Xt Ve
k
jwkt
k n
n
()=
=−
∑
. (2.1)
Случайные величины V
k
являются центрированными, корреляционно
независимыми: M[V
k
]=0, M[V
k
V
j
]=0, M[V
k
V
k
]=d
k
.
Коэффициенты d
k
представляют средние значения квадратов случайных амплитуд гармоник, из
которых составлен процесс X(t).
2.1. Характеристики случайных процессов
Математическим ожиданием случайного процесса называется
неслучайная функция Mx(t), значение которой в каждый момент времени
равно математическому ожиданию случайной величины X(t):
Mxt Xtfxtdx() ()(,) .=
−∞
∞
∫
Математическое ожидание определяет среднее значение процесса.
15
Дисперсией случайного процесса X(t) называется неслучайная функция
времени Dx(t), значение которой в каждый момент времени равно дисперсии
соответствующей случайной величины:
[ ]
{
}
Dxt M Xt Mxt() () ()= −
2
. (2.2)
Дисперсия определяет спектральную мощность процесса.
Среднеквадратическое отклонение равно квадратному корню из
дисперсии
σ = Dx
(2.3)
и характеризует разброс процесса относительно среднего значения.
Корреляционной функцией случайного процесса X(t) называется
неслучайная функция двух аргументов времени t, t’, значение которой равно
корреляционному моменту случайных величин, взятых в эти моменты
времени: Kx(t,t')=M{[X(t)-Mx(t)][X(t')-Mx(t')]}. Эта функция характеризует
степень статистической зависимости между двумя сечениями процесса.
Взаимокорреляционной функцией процессов X(t), Y(t) называется
неслучайная функция двух аргументов времени, значение которой равно
корреляционному моменту случайных величин, взятых в соответствующие
моменты времени: Kxy(t,t')=M{[X(t)-Mx(t)][Y(t')-My(t')]}.
Взаимокорреляционная функция характеризует степень статистической
зависимости процессов.
Спектральной плотностью процесса X(t) является преобразование Фурье
от корреляционной функции:
Sxw Rx e d
jw
() ()=
−
−∞
∞
∫
τ τ
τ
. (2.4)
Спектральная плотность характеризует распределение дисперсии по w.
Наибольшее значение названные статистические характеристики имеют
для стационарных эргодических процессов. Стационарность в широком
смысле означает, что математическое ожидание случайного процесса
постоянно, а корреляционная функция зависит только от разности
аргументов: τ=t-t'. Эргодичность процесса означает, что математическое
ожидание по множеству реализаций процесса может быть найдено как
среднее по времени в одной из реализаций:
Mxt
T
Xtdt
T
T
() lim ()=
→∞
∫
1
0
, где Т -
длительность реализации случайного процесса.

16
Рассмотрим свойства числовых характеристик случайных сигналов.
Свойства математического ожидания. 1. Математическое ожидание
линейного преобразования случайной функции F(X) равно линейному
преобразованию от математического ожидания этой функции
M[L{F(X)}]=L{M[F(X)]}, где L - оператор линейного преобразования (сумма,
интеграл, производная, линейное дифференциальное уравнение, матричное
линейное преобразование и т.п.).
Пример. Пусть линейная функция
FX X t t
j j
j
n
( ) [ () ()]= +
=
∑
Φ
1
, где Фj(t) -
неслучайные функции времени. Математическое ожидание F(X) в этом
случае имеет вид
[ ]
[ ]
{ }
MFX MX t t
j j
j
n
( ) () ()= +
=
∑
Φ
1
.
2. Вектор математических ожиданий M[X]={M[x
1
],...,M[x
n
]}
т
.
Пример. Пусть функция F(X) имеет вид F(X)=A(t)X(t)+B(t)U(t), где A(t),
B(t) - матрицы детерминированных функций (в частном случае
коэффициентов); U(t), X(t) - векторы соответственно неслучайных и
случайных функций. Получим математическое ожидание F(X):
M[F(X)]=A(t)M[X(t)]+B(t)U(t).
Свойства корреляционной функции:
1) |Rx(r)|≤ Rx(0);
2) Rx(-r)=Rx(r);
3) Rx(0)=Dx;
4) r
x
=Rx(r)/Dx - нормированная корреляционная функция, 0≤|r
x
|≤1;
5) при Z=X+Y имеем Rz(r)=Rx(r)+Ry(r)+Rxy(r)+Ryx(r);
6) при Y(t)=L{X(t)} имеем Ry(r)=LL'{Rx(t)};
7) Kxy(t,t')=M[X(t)Y(t')]-M[X(t)]M[Y(t')].
Пример. Корреляционная функция случайного сигнала (2.1) имеет вид
R de
k
jwk
k
n
n
()τ
τ
=
=−
∑
. Дисперсия X(t) на основании свойства Dx=R(o) в этом
случае определяется выражением
Dx d
k
k n
n
=
=−
∑
.
Свойства спектральной плотности. 1) S(w)=S(-w) - свойство четности; 2)
вычисление дисперсии через спектральную плотность:
17
Dx Sxwdw=
−∞
∞
∫
1
2π
()
; (2.5)
3) S(w)≥ 0 - свойство неотрицательности; 4) Sxy(-w)=Syx(w) - свойство
взаимоспектральной плотности.
Пример. Спектральная плотность белого шума, найденная по (2.4):
Svw N e d N
jw
() ()= =
−
−∞
∞
∫
δτ τ
τ
, где N - интенсивность шума.
2.2. Прохождение процесса через линейную динамическую систему
При прохождении случайного сигнала через линейную динамическую
систему (ДС) изменяются его характеристики: математическое ожидание,
корреляционная функция, спектральная плотность, взаимокорреляционная
функция, взаимоспектральная плотность. При обозначении линейного
преобразования оператором L{t} или в частотной области W(jw) выходной
процесс определяется выражениями y(t)=L{x(t)}, Y(jw)=W(jw)X(jw). На
основании свойств математического ожидания и корреляционной функции
имеем изменение этих характеристик в виде M[L{X}]=L{M[X]},
Ry(τ)=LL'{Rx(τ)}, где L' - линейное преобразование по времени t+r.
Изменение спектральной плотности определяется в частотной области [7]:
Sy(w)=Sx(w)|W(jw)|
2
, где W(jw) - амплитудно-фазочастотная характеристика
системы. Взаимоспектральная плотность процессов X и Y имеет вид [7]
Sxy(jw)=Sx(w)W(jw), Syx(jw)=Sx(w)W(-jw). На основе этих свойств
определяется формирующий фильтр процесса.
Формирующий фильтр - это линейная ДС, на входе которой белый шум с
интенсивностью Q, а на выходе сигнал со спектральной плотностью
Sg(w)=QWg(jw)Wg(-jw), где Wg(jw) - амплитудно-фазочастотная
характеристика фильтра.
2.3. Расчет числовых характеристик случайных процессов
При изучении случайных сигналов важным является исследование их
статистических характеристик: математического ожидания, дисперсии,
корреляционной функции, спектральной плотности. Здесь исследуются
стационарные эргодические процессы, которые представляются дискретными
значениями, взятыми через достаточно короткие промежутки времени
X(t
k
)=X(k) (на основании импульсной теоремы). В этом случае интеграл в
18
математическом ожидании вычисляется через сумму. Расчетные формулы
статистических характеристик [8]:
математическое ожидание
Mx
n
Xk
k
n
=
=
∑
1
1
()
;
корреляционная функция
RxrT
n r
XkXk r
k
nr
( ) () ( ),=
−
+
=
−
∑
1
1
где r=0,1,...,m
- шаг (m≤0,2n); T - период дискретизации;
спектральная плотность
Sk Sf
k
m
TR R j
k
m
R
c j
j
m
k
m
() ( ) cos( ) ( )= = + +−
=
−
∑
2 2 1
0
1
1
π
,
где f
c
- частота среза сигнала.
Дисперсия находится через корреляционную функцию или спектральную
плотность:
Dx R
mT
S Sk S
m
k
m
= = + +
=
−
∑
() ()0
1
2
1
2
1
2
0
1
1
.
В связи с трудоемкостью вычислений статистических характеристик
случайных процессов необходимо использовать ЦВМ, где процедуры расчета
легко программируются. Эффективность автоматизированного расчета на
ПЭВМ проявляется также в достаточной точности оценивания числовых
характеристик при использовании больших объемов выборки.
3. МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ И ПРОЦЕССОВ
3.1. Модели динамических систем и процессов
В современной математике используется представление динамических
процессов и систем дифференциальными уравнениями в пространстве
состояний. Такое описание процессов и систем позволяет проводить их
цифровое моделирование [9-12] и проектировать универсальные алгоритмы
обработки информации с целью оптимального оценивания параметров систем
и процессов [13-20]. Оптимальные оценки используются для организации
управления в системах автоматического управления (САУ) современными
методами, а в информационно-измерительных системах (ИИС) для получения
достоверных данных об измеряемых физических величинах, для
19
прогнозирования, повышения отказоустойчивости обработки информации
[21,22].
Необходимо уметь формировать различного типа математические модели
(динамические модели кибернетических систем, процессов) с дальнейшей их
реализацией (исследованием) на ПЭВМ путем вычислительного
эксперимента. Одним из методов получения математической модели системы
или процесса является идентификация.
Идентификацией динамической системы (процесса) называется
получение или уточнение по экспериментальным данным математической
модели этой системы или процесса, выраженной посредством того или иного
математического аппарата [7].
Непрерывной детерминированно-стохастической ДС называется система,
описываемая линейными дифференциальными уравнениями первого порядка
состояния (матричным линейным уравнением) и линейным уравнением
выхода
X′ (t)=AХ(t)+BU(t)+DV(t), Y(t)=CX(t), (3.1)
где Х(t) - n-мерный вектор состояния системы; V(t)- r-мерный вектор
гауссовских шумов с нулевым средним и корреляционной матрицей
E[V(t)V
т
(t)]=Q(t) (Е - оператор математического ожидания); Y(t) - m-мерный
вектор выхода; A, B, D - матрицы состояния (матрицы коэффициентов); С -
матрица линейного преобразования размера m×n. Для моделирования
процессов и систем на ПЭВМ составляются дискретные модели в виде
стохастических линейных разностных уравнений первого порядка.
Дискретной детерминированно-стохастической ДС называется система,
описываемая линейными разностными уравнениями первого порядка
состояния и дискретным уравнением выхода
Х(k+1)=F(k+1,k)Х(k)+G(k+1,k)U(k)+T(k+1,k)V(k), Y(k)=CX(k), (3.2)
где F(k+1,k), G(k+1,k), T(k+1,k), - переходные матрицы. В стацио-нарном
случае (при независимости от времени k) F(k+1,k)=F, G(k+1,k)=G,
T(k+1,k)=T. Матрицы F, G, T зависят от A, B, D и вычисляются в виде [5]
