Витяев Е.Е. Извлечение знаний из данных. Компьютерное познание. Модели когнитивных процессов (2006)

Подождите немного. Документ загружается.

111

(удовлетворяют условию 1 (определение 37)). Отсюда следует свойство 2

(определение 37) P-предсказания ■

§ 42. Взаимосвязь вероятностного и логического выводов

Пусть Pr – некоторая логическая программа, факты которой содержатся

среди фактов D(N) программы PR(M, N) = P(M) ∪ D(N).

Теорема 15. Если атом A предсказывается программой Pr c оценкой

η(A) > µ(Aθ), для любой подстановки θ ∈ ΘG, то он P-предсказывается

программой PR(M, N) с оценкой P-предсказания η

(A) > η(A).

Доказательство. По условию существует успешный SLDF-вывод

Aθ, N

θ, ..., N

, N

∈ ℜ цели Aθ в пространстве вычислений программы

Pr такой, что µ(Aθ / N

) ≥ η(A) > µ(Aθ), µ(N

) > 0, N

= ← B

, ..., B

;

← , ..., B

← } ⊂ Pr, l > 1.

Рассмотрим правило C = Aθ ← B

, ..., B

. Из условия η(A) > µ(Aθ) ≥ 0,

следует что l ≥ 1. Так как µ(N

) > 0, то C ∈ PR0. Кроме того, µ(C) ≥ η(A)

> µ(Aθ) и, следовательно, выполнено условие 1 (определение 34) наилуч-

шего для предсказания атома A правила. Отсюда следует, что существует

наилучшее для предсказания атома A правило CB и по теореме P-

предсказание атома A определено и η

(A) = µ(CB). Так как правило, C

удовлетворяет условию 1 (определение 34), то η

(A) = µ(CB) ≥ µ(C) по ус-

ловию 2 этого же определения ■

Рассмотрим P-предсказание C

⊏ ... ⊏ C

⊏ ... цели A программой

PR(M, N) = P(M) ∪ D(N) по наилучшему для предсказания атома A прави-

лу C

= A

← B

, ..., B

и подстановке θ, {B

θ, ..., B

θ} ⊂ D(N), Aθ = A

θ,

µ(A

) < µ(C

). Этому P-предсказанию поставим в соответствие нормализо-

ванный SLDF-вывод, который будем обозначать как SLDP(A)-вывод,

← Aθ; ← B

θ, ..., B

θ; ... ; ← B

θ, ..., B

θ цели Aθ по правилам C

θ ← , ..., B

θ ← . По теореме 4.2 найдем оценку η полученного

SLDP(A)-вывода: µ(Aθ / N

) ≥ η = 1 - (1 - p)µ(B

θ& ... &B

θ) / µ(N

) =

1 - (1 - p) = p, где p = µ(C

Таким образом, η(A) ≥ η = µ(C

) = η

(A). SLDP(A)-вывод цели A состо-

ит в использовании наилучшего для предсказания атома A правила C

фактов D(N) программы.

Теорема 16. Если атом A предсказывается программой PR(M, N) с

оценкой η(A) > µ(Aθ), θ ∈ ΘG и P-предсказывается этой же программой с

оценкой η

(A), то η(A) = η

(A).

Доказательство. Выше, при введении понятия SLDP(A)-вывода, было

доказано, если P-предсказание атома A определено, то существует

SLDP(A)-вывод атома A такой, что η(A) ≥ η

(A). Обратное неравенство

112

(A) ≥ η(A) следует из теоремы, если в качестве программы Pr взять про-

грамму PR(M, N) ■

Теорема 17. Если атом A предсказывается некоторой программой Pr с

оценкой η(A) > µ(Aθ), θ ∈ ΘG, то он предсказывается программой

PR(M, N) с оценкой η'(A), η'(A) ≥ η(A).

Доказательство. В силу теоремы, атом A P-предсказывается програм-

мой PR(M, N) с оценкой η

(A) ≥ η(A). Из предыдущих рассуждений сле-

дует, что в этом случае существует SLDP(A)-вывод атома A программой

PR(M, N) с оценкой η = η

(A) ≥ η(A) > µ(Aθ), θ ∈ ΘG. Отсюда следует,

что предсказание атома A программой PR(M, N) определено и для оценки

предсказания η'(A) имеет место соотношение η'(A) ≥ η = η

(A) ■

Процесс организации вычислений запросов ← A

, ..., A

, k ≥ 2 можно

охватить, обобщив понятие вероятностной закономерности на утвержде-

ния A

& ... &A

← B

, ..., B

113

ГЛАВА 4. РЕЛЯЦИОННЫЙ ПОДХОД

К ИЗВЛЕЧЕНИЮ ЗНАНИЙ ИЗ ДАННЫХ

§ 43. Логический анализ методов извлечения знаний

В данном параграфе проводится логический анализ методов Machine

Learning и KDD&DM. Показывается, что если методы не основаны на тео-

рии измерений, то для них возникает проблема адекватности – доказатель-

ство инвариантности метода относительно допустимых преобразований

шкал. В противном случае метод может давать различные результаты в за-

висимости от того в каких единицах измерения представлены данные.

Вводится определение инвариантности метода относительно выбора чи-

словых представлений для данных. Выделяется логическая составляющая

данных. Показывается, как для любого метода Machine Learning и

KDD&DM можно получить его логический аналог, для которого не возни-

кает проблема инвариантности.

В результате проведенного анализа показывается, как для каждого

Machine Learning и KDD&DM можно выделить:

- тип данных с которыми работает KDD&DM-метод в виде много-

сортной эмпирической системы;

- онтологию метода в виде множества отношений и операций, в ко-

торых записаны данные и представлены гипотезы метода;

- тип знаний метода как класс правил, которые проверяет метод.

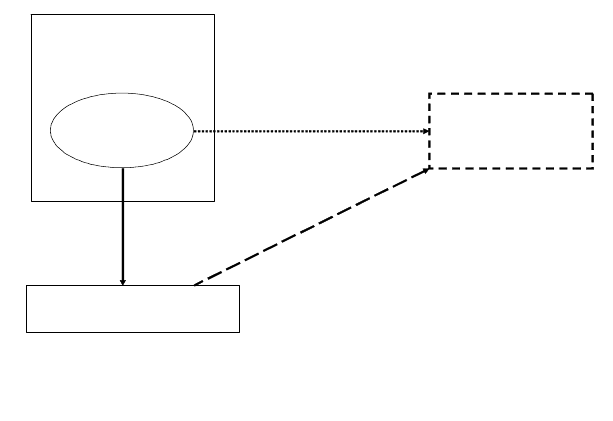
Дадим определение инвариантности метода. Для этого представим чи-

словые методы, как это показано на рис 8 :

- W = {w} – обучающая выборка;

- X(w) = (x1, …, xn) – набор значений из n признаков для каждого

объекта обучения;

- Y(w) – целевое значение признака для каждого объекта обучения

KDD&DM метод M в результате обучения на обучающей выборке

{X(w)}, w∈W, порождает решающее правило

J = M({X(w)}),

которое предсказывает целевые значения признака Y(w). Например, рас-

смотрим объект w с неизвестным значением Y(w), но известными значе-

ниями признаков X(w), тогда

J(X(w)) ~ Y(w),

где J(X(w)) является значением сгенерированным правилом J, и ~ прибли-

зительное равенство. Решающее правило J может

быть алгебраическим

или логическим выражением, решающим деревом, нейронной сетью или

гибридным алгоритмом.

114

Для признаков (x

, …, x

, Y) существуют эмпирические системы

, …, A

, B, имеющие соответствующие группы преобразований

, …, g

, g. Группа преобразований для всех признаков определяется как

группа G = g

× … × g

× g.

Инвариантность KDD&DM-метода M относительно группы преобразо-

ваний G определяется так, что для любого преобразования g∈G решающее

правило обнаруживаемое методом М должно быть одним и тем же в том

смысле, что принимаемые на объектах w∈W решения совпадают, т.е. ре-

шающие правила J = M({〈X(w), Y(w)〉}) и J

= M({〈gX(w), gY(w)〉}), полу-

ченные методом М по преобразованной {〈gX(w), gY(w)〉} и не преобразо-

ванной {〈X(w), Y(w)〉} выборке должны давать одни и те же решения для

любых объектов w∈W

(g(X(w))) = g(J(X(w))),

J = M({〈X(w), Y(w)〉}), J

= M({〈gX(w), gY(w)〉}).

Если метод не инвариантен, то получаемые методом решения зависят

от выбора единиц измерения.

Инвариантность метода тесно связана с интерпретируемостью его ре-

зультатов. Если метод не инвариантен, то его результаты не могут быть

полностью интерпретируемы. Интерпретируемость результатов означает

их интерпретируемость в системе понятий предметной области.

Генеральная

совокупность

Представление обучающих

объектов набором признаков:

...., x

)= X(w)

Целевые значения

Y(w)

Assigning (learning)

rule/classifier J by the

KDD&DM method M

M({〈X(w),Y(w)〉}) = J,

J(X(w)) ~ Y(w)

Y(w)

X(w)

Обучающая

выборка

W={w}

{X(w)}={(x

...., x

)}

Присвоение целевых значений

Объектам обучения

Рис 8.

115

Эмпирические системы A

, …, A

, B признаков, по определению, ин-

терпретируемы в системе понятий предметной области. Методы

KDD&DM очевидно инвариантны, если они используют в своей работе

только интерпретируемую информацию эмпирических систем A

, …, A

, B

и обнаруживают решающие правила J, являющиеся логическими выраже-

ниями в терминах эмпирических систем.

Покажем, как из любого метода KDD&DM можно извлечь инвариант-

ный метод M : {X(w)} → J. Проанализируем метод M с точки зрения огра-

ничений KDD&DM-методов 1–3. Определим многосортную эмпириче-

скую систему A(W) как произведение эмпирических систем A

, …, A

, B.

Эмпирическая система A(W) содержит всю интерпретируемую информа-

цию относительно обучающей выборки W. Обозначим через W → A(W)

преобразование выборки в многосортную эмпирическую систему A(W),

извлекающую всю интерпретируемую информацию из данных в соответ-

ствии с теорией измерений. Преобразование

W → {〈X(w), Y(w)〉}

заменим на преобразование

W → A(W) → {〈X(w), Y(w)〉}.

Метод

M :{〈X(w), Y(w)〉} → J

преобразуем в метод

ML :A(W) → J

таким образом, чтобы метод ML делал все то же самое, что и метод M,

только вместо выборки W использовал соответствующую ей эмпириче-

скую систему A(W) и все действия, которые осуществляет метод М пере-

водил бы в действия над эмпирической системой. Точнее, если числовые

представления признаков (x

, …, x

, Y) получены сильными гоморфизмами

: A

→ Re

, φ : B → Re

то комплексное преобразование

(φ

, …, φ

, φ) :A(W) → {〈X(w), Y(w)〉}

переводит многосортную эмпирическую систему в числовое представле-

ние выборки. Отсюда получаем

J = M({〈X(w), Y(w)〉}) = М((φ

, …, φ

, φ)(A(W))) = ML(A(W)).

Извлечем из правила J некоторое правило JL, содержащее всю интер-

претируемую правила J. Для этого преобразуем правило

J(X(w)) = J((φ

, …, φ

)A(w)) = JL(A(w)) ~ Y(w).

На основании метода ML и правила JL можно определить инвариант-

ный метод

MLogic: A(W) → JL

следующим образом:

116

MLogic(A(W)) = ML(A(W)) = J(X(w)) = JL(A(w)).

Метод MLogic очевидно инвариантен. Если мы рассмотрим все воз-

можные выборки для метода М и получим все правила JL методом

MLogic, то мы получим класс гипотез {JL} (тип знаний) метода M.

В результате проведенного анализа мы получили:

тип данных, с которыми работает KDD&DM-метод M в виде мно-

госортной эмпирической системы A(W);

онтологию метода в виде множества отношений и операций, в ко-

торых записаны данные и представлены гипотезы;

тип знаний метода M как класс правил {JL}.

В отличие от конкретного KDD&DM-метода разработанная в рамках

реляционного подхода система

Discovery не имеет ограничений ни в типе

данных, ни в онтологии, ни в классе обнаруживаемых знаний.

§ 44. Реляционный подход к извлечению знаний

В реляционном подходе к извлечению знаний следующим образом

снимаются все ограничения с существующих ML, KDD&DM-методов:

ограничения с используемых типов данных за счет использования

теории измерений и многосортных эмпирических систем;

2) использование теории измерений позволяет извлекать всю инфор-

мацию из данных, что не делают другие методы;

3) ограничения в использовании априорного знания путем представ-

ления априорного знания в логике первого порядка;

4) ограничения с классов проверяемых гипотез за счет введения типа

обнаруживаемых знаний Rule Type в языке первого порядка;

5) разработана система Discovery, которая обнаруживает все перечис-

ленные ниже виды множеств:

a) множество законов L на эмпирической системе М;

b) множество МСЗ максимально специфических правил;

c) множество правил с максимальными оценками условной вероятно-

сти.

В реляционном подходе система обнаруживаемых знаний, которые

могут составить базу знаний, полна в двух смыслах:

― в смысле полноты извлечения информации из данных за счет ис-

пользования теории измерений;

― полноты обнаруживаемых множеств правил a-c;

§ 45. Программная система извлечения знаний «Discovery»

Программная система Discovery реализует семантический вероятност-

ный вывод и обнаруживает перечисленные в предыдущем параграфе в

п.5

а–c множества законов, вероятностных законов, сильнейших вероятно-

117

стных законов и максимально специфических правил на данных. Естест-

венно, что на данных нам не известны вероятности и их необходимо оце-

нивать по данным. Способ оценки и используемый статистический крите-

рий приведены далее в § 46.

Система

Discovery позволяет реализовать стратегию направленного и

все более детального анализа эмпирического содержания данных, задавая

последовательно уточняющиеся параметрические семейства формул (1)

[18–19; 30–31; 36; 127; 131]. Эта стратегия согласуется с теорией измере-

ний, показывающей, что шкалы величин упорядочены в соответствии с бо-

гатством информации, содержащейся в значениях величин – от шкалы на-

именований и шкалы порядка к шкале интервалов

, отношений и абсолют-

ной шкале.

В соответствии с этой стратегией сначала следует провести грубую об-

работку данных в шкале наименований. Имеющиеся числовые значения

следует разбить на интервалы, которые можно задавать параметрами. За-

тем следует найти все закономерности в шкале порядка и наименований.

После такой обработки все признаковое пространство разобьется на

облас-

ти, выделяемые именами или интервалами, внутри которых будет иметь

место монотонная зависимость в шкале порядка между некоторыми при-

знаками.

Более точный анализ вида зависимости должен проводиться за счет

информации, содержащейся в более сильных шкалах, используя соответ-

ствующие этим шкалам отношения и операции. Для этого следует прове-

рить выполнимость известных систем

аксиом теории измерений на обна-

руженных участках монотонности. Это можно сделать системой

Discovery,

проверяя выполнимость заложенных в ней систем аксиом теории измере-

ний. Если какая-либо система аксиом выполнена, то это позволяет опреде-

лить вид функциональной зависимости и адекватные решаемой задаче

шкалы величин.

§ 46. Метод обнаружения вероятностных законов

Понятие вероятностного закона требует проверки некоторых вероятно-

стных неравенств. Проверить выполнимость этих вероятностных нера-

венств на выборке из серии экспериментов можно с помощью определен-

ных статистических критериев. Предположим, что случайно и независимо

в соответствии с вероятностной мерой µ проведена серия экспериментов и

получена выборка экспериментов Samp ⊂ Exp.

Для статистической проверки любой аксиомы

из Σ нам достаточно

иметь статистику – число повторений каждого события из высказывания.

Получение этой статистики упрощается тем, что нам достаточно знать

только статистику для всех атомов, входящих в высказывание. Статистика

118

любого события является суммой статистик тех атомов, из которых состо-

ит событие. Статистику для атомов можно представить в виде специально-

го массива.

Определим массив M объема 2

к+1

в соответствии с числом атомарных

формул P

, P

, ..., P

в правиле (1). Значения истинности каждой ато-

марной формулы зададим числами 1, 0 (1 – «истина» и 0 – «ложь»). Каж-

дый элемент массива M[i

, ..., i

к+1

], i

, ..., i

к+1

∈ {0, 1} равен числу сочетаний

значений истинности i

, ..., i

к+1

атомарных формул P

, P

, ..., P

в экспе-

риментах Samp (после фиксации интерпретации, подстановки объектов

вместо переменных и определения значений истинности атомарных фор-

мул). В дальнейшем мы будем предполагать, что статистика (число случа-

ев) любого события D булевой алгебры событий B порожденной атомар-

ными формулами P

, P

, ..., P

нам известна и будем обозначать ее через

κ(D).

Проверим сначала для некоторого правила C = (A

& ... &A

⇒ A

) вида

(1), что выполнено первое условие вероятностной закономерности: что ус-

ловная вероятность определена и η(A

& ... &A

) > 0. Для этого достаточно

проверить, что κ[A

& ... &A

] > 0. Из определения вероятности

(определение 13) следует, что если κ[A

& ... &A

] > 0, то вероятность не

равна 0. На этом проверка первого условия заканчивается.

Перейдем к проверке второго условия. Рассмотрим сначала правила

вида P

ε1

⇒ P

ε0

. Так как в посылке стоит только один предикатный символ

ε1

, который можно удалить в процессе обобщения, то по определению

вероятностного закона (определение 17) вероятность правила C = ( ⇒ P

ε0

)

с пустой посылкой должна быть строго меньше условной вероятности

правила P

ε1

⇒ P

ε0

, т. е.

η(P

ε0

/ P

ε1

) > η(P

ε0

Последнее неравенство можно переписать в виде

η(P

ε0

ε1

) > η(P

ε0

)* η(P

ε1

Для проверки этого неравенства сформулируем гипотезу H

о незави-

симости предикатных символов P

ε1

и P

ε0

: η(P

ε0

ε1

) = η(P

ε0

)* η(P

ε1

против альтернатив:

: η(P

ε0

ε1

) ≠ η(P

ε0

)* η(P

ε1

Эта гипотеза является сложной с одним ограничением и двумя степе-

нями свободы [51]. Если гипотеза H

верна, то предикатные символы P

ε1

ε0

независимы и неравенство для условной вероятности не выполнено.

Тогда формула P

ε1

⇒ P

ε0

не является вероятностной закономерностью.

Если гипотеза H

неверна, то верна одна из альтернативных гипотез H

тогда значения P

ε1

и P

ε0

зависимы между собой.

119

Гипотезу H

можно переформулировать также следующим образом.

Пусть числа κ(P

ε1

) и κ(P

(1-ε1)

) фиксированы, а числа κ(P

ε1

ε0

) и

κ(P

(1-ε1)

ε0

) являются независимыми случайными величинами. Тогда

гипотеза H

является гипотезой о равенстве вероятностей в двух совокуп-

ностях [51]:

: η(P

ε0

ε1

) = η(P

ε0

)* η(P

ε1

против альтернатив:

: η(P

ε0

ε1

) ≠ η(P

ε0

)* η(P

ε1

Если гипотеза H

неверна, то верна одна из гипотез H

, и либо

η(P

ε0

/ P

ε1

) > η(P

ε0

), либо η(P

ε0

/ P

ε1

) < η(P

ε0

Если верно первое неравенство, то тестируемая формула

ε1

⇒ P

ε0

является вероятностной закономерностью, если второе, то не является.

По соотношениям

κ(P

ε0

ε1

) > (κ(P

ε0

)* κ(P

ε1

)) / N,

κ(P

ε0

ε1

) < (κ(P

ε0

)*κ(P

ε1

)) / N,

где N – общее количество экспериментов, можно определить, какое из не-

равенств первое или второе имеет место.

Чтобы проверить гипотезу H

против альтернатив H

воспользуемся

точным критерием независимости Фишера [Там же; с. 739]. Этот критерий

является равномерно наиболее мощным, несмещенным критерием как в

случае проверки гипотезы о двумерной независимости, так и в случае про-

верки гипотезы о равенстве вероятностей в двух совокупностях [Там

же; с. 742]. Применив этот критерий с некоторым доверительным уровнем

α, мы получим,

что,либо гипотеза H

верна и, следовательно, значения ис-

тинности предикатных символов P

ε1

и P

ε0

независимы и, значит, нет ни-

какой закономерности, либо H

не верна и мы принимаем одну из гипотез

. Если гипотеза H

означает, что η(P

ε0

ε1

) > η(P

ε0

)* η(P

ε1

), то тести-

руемая формула является вероятностной закономерностью с доверитель-

ным уровнем α.

Рассмотрим в общем случае произвольную аксиому

C = (P

ε1

& … &P

εn

⇒ P

ε0

) ∈ S. Сведем этот случай к предыдущему. Вве-

дем обозначения DC = {P

ε1

, …, P

εn

}, D ⊂ DC (включение строгое), DC

ε1

& … &P

εn

, D

– конъюнкция литер из D.

Для проверки является ли аксиома С вероятностной закономерностью,

надо проверить, выполняется ли для любого подмножества D (включая ∅)

соотношение

η(P

ε0

/ DC

) > η(P

ε0

/ D

120

Будем рассматривать конъюнкцию D

как одну формулу R

из ℜ(Σ), а

конъюнкцию литер из DC \ D как другую формулу R

из ℜ(Σ). В случае,

когда D = ∅, R

= true, а η(P

ε0

/ D

) = η(P

ε0

). Тогда получим неравенство

η(P

ε0

/ R

) > η(P

ε0

/ R

Так как

η(P

ε0

/ R

) = η(P

ε0

) / η(R

) = η(P

ε0

/ R

) / η(R

/ R

то предыдущее неравенство перейдет в неравенство

η(P

ε0

/ R

) > η(R

/ R

)* η(P

ε0

/ R

Так как κ[A

& ... &A

] > 0, то η(DC&) > 0; η(R

) > 0; η(R

) > 0 в силу

включений D ⊂ DC и DC \ D ⊂ DC. Отсюда следует, что все проделанные

преобразования корректны, так как ни одна вероятность в знаменателе не

равна 0.

Для проверки последнего неравенства также сформулируем гипотезу о

независимости

: η(P

ε0

/ R

) = η(R

/ R

)* η(P

ε0

/ R

)

против альтернатив:

: η(P

ε0

/ R

) ≠ η(R

/ R

)* η(P

ε0

/ R

Ограничимся рассмотрением только тех событий, для которых формула

истинна. Для этого определим подалгебру ℜ(Σ)(R

) булевой алгебры

ℜ(Σ), рассматривая только события на которых R

истинна. На этих собы-

тиях определим вероятностную меру η’(E) = η(E&R

) / η(R

). Тогда гипо-

тезы H

и H

примут вид:

: η’(P

ε0

) = η’(R

)* η’(P

ε0

: η’(P

ε0

) ≠ η’(R

)* η’(P

ε0

Гипотеза H

проверяется также с помощью критерия Фишера с некото-

рым доверительным уровнем α.

Правило C будем вероятностным законом с доверительным уровнем α,

если гипотеза H

отвергается с уровнем α для любого подмножества

D ⊂ DС и принимается гипотеза H

с неравенством >.

Если аксиома С не является вероятным законом, то необходимо прове-

рить не является ли какая-нибудь более общая часть аксиомы C вероятно-

стным законом. Для этого в качестве DС надо брать последовательно все

возможные подмножества D ⊂ DС условий посылки правила и для каждо-

го D’ ⊂ D ⊂ DС снова проверять

все гипотезы и неравенства с целью опре-

делить является ли правило с посылкой D вероятностным законом.